8.5: Limiting Reactant, Theoretical Yield, and Percent Yield
- Page ID
- 98043
↵
- Identify the limiting reactant (limiting reagent) in a given chemical reaction.
- Calculate how much product will be produced from the limiting reactant.
- Calculate how much reactant(s) remains when the reaction is complete.
In all examples discussed thus far, the reactants were assumed to be present in stoichiometric quantities. Consequently, none of the reactants were left over at the end of the reaction. This is often desirable—as in the case of a space shuttle—where excess oxygen or hydrogen is not only extra freight to be hauled into orbit, but also an explosion hazard. More often, however, reactants are present in mole ratios that are not the same as the ratio of the coefficients in the balanced chemical equation. As a result, one or more of them will not be used up completely, but will be left over when the reaction is completed. In this situation, the amount of product that can be obtained is limited by the amount of only one of the reactants. The reactant that restricts the amount of product obtained is called the limiting reactant. The reactant that remains after a reaction has gone to completion is in excess.
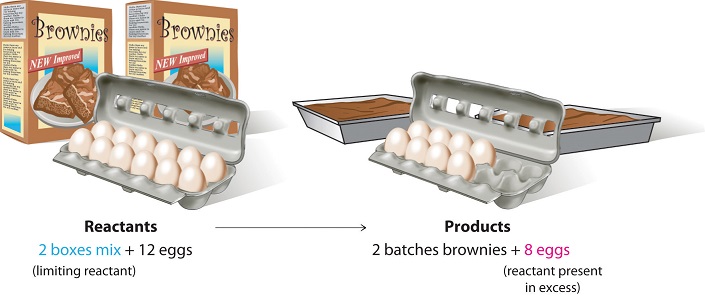
Consider a nonchemical example. Assume you have invited some friends for dinner and want to bake brownies for dessert. You find two boxes of brownie mix in your pantry and see that each package requires two eggs. The balanced equation for brownie preparation is:
\[ 1 \,\text{box mix} + 2 \,\text{eggs} \rightarrow 1 \, \text{batch brownies} \label{3.7.1} \]
If you have a dozen eggs, which ingredient will determine the number of batches of brownies that you can prepare? Because each box of brownie mix requires two eggs and you have two boxes, you need four eggs. Twelve eggs is eight more eggs than you need. Although the ratio of eggs to boxes in is 2:1, the ratio in your possession is 6:1. Hence the eggs are the ingredient (reactant) present in excess, and the brownie mix is the limiting reactant. Even if you had a refrigerator full of eggs, you could make only two batches of brownies.
View this interactive simulation illustrating the concepts of limiting and excess reactants.
Consider this concept now with regard to a chemical process, the reaction of hydrogen with chlorine to yield hydrogen chloride:
The balanced equation shows that hydrogen and chlorine react in a 1:1 stoichiometric ratio. If these reactants are provided in any other amounts, one of the reactants will nearly always be entirely consumed, thus limiting the amount of product that may be generated. This substance is the limiting reactant, and the other substance is the excess reactant. Identifying the limiting and excess reactants for a given situation requires computing the molar amounts of each reactant provided and comparing them to the stoichiometric amounts represented in the balanced chemical equation. For example, imagine combining 3 moles of H2 and 2 moles of Cl2. This represents a 3:2 (or 1.5:1) ratio of hydrogen to chlorine present for reaction, which is greater than the stoichiometric ratio of 1:1. Hydrogen, therefore, is present in excess, and chlorine is the limiting reactant. Reaction of all the provided chlorine (2 mol) will consume 2 mol of the 3 mol of hydrogen provided, leaving 1 mol of hydrogen non-reacted.
An alternative approach to identifying the limiting reactant involves comparing the amount of product expected for the complete reaction of each reactant. Each reactant amount is used to separately calculate the amount of product that would be formed per the reaction’s stoichiometry. The reactant yielding the lesser amount of product is the limiting reactant. For the example, in the previous paragraph, complete reaction of the hydrogen would yield:
\[\mathrm{mol\: HCl\: produced=3\: mol\:H_2\times \dfrac{2\: mol\: HCl}{1\: mol\:H_2}=6\: mol\: HCl} \nonumber \]
Complete reaction of the provided chlorine would produce:
\[\mathrm{mol\: HCl\: produced=2\: mol\:Cl_2\times \dfrac{2\: mol\: HCl}{1\: mol\:Cl_2}=4\: mol\: HCl} \nonumber \]
The chlorine will be completely consumed once 4 moles of HCl have been produced. Since enough hydrogen was provided to yield 6 moles of HCl, there will be non-reacted hydrogen remaining once this reaction is complete. Chlorine, therefore, is the limiting reactant and hydrogen is the excess reactant (Figure \(\PageIndex{2}\)).
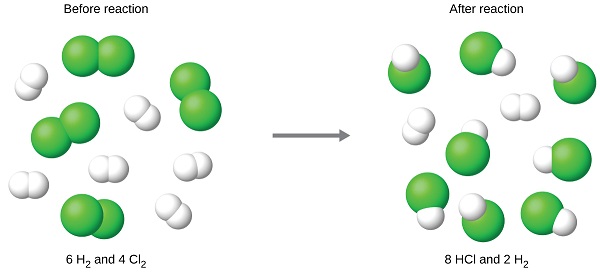
A similar situation exists for many chemical reactions: you usually run out of one reactant before all of the other reactant has reacted. The reactant you run out of is called the limiting reactant; the other reactant or reactants are considered to be in excess. A crucial skill in evaluating the conditions of a chemical process is to determine which reactant is the limiting reactant and which is in excess.
There are two ways to determine the limiting reactant. One method is to find and compare the mole ratio of the reactants used in the reaction (Approach 1). Another way is to calculate the grams of products produced from the given quantities of reactants; the reactant that produces the smallest amount of product is the limiting reactant (Approach 2). This section will focus more on the second method.
Approach 1 (The "Reactant Mole Ratio Method"): Find the limiting reactant by looking at the number of moles of each reactant.
- Determine the balanced chemical equation for the chemical reaction.
- Convert all given information into moles (most likely, through the use of molar mass as a conversion factor).
- Calculate the mole ratio from the given information. Compare the calculated ratio to the actual ratio.
- Use the amount of limiting reactant to calculate the amount of product produced.
- If necessary, calculate how much is left in excess of the non-limiting (excess) reactant.
Approach 2 (The "The Product Method"): Find the limiting reactant by calculating and comparing the amount of product that each reactant will produce.
- Balance the chemical equation for the chemical reaction.
- Convert the given information into moles.
- Use stoichiometry for each individual reactant to find the mass of product produced.
- The reactant that produces a lesser amount of product is the limiting reactant.
- The reactant that produces a larger amount of product is the excess reactant.
- To find the amount of remaining excess reactant, subtract the mass of excess reactant consumed from the total mass of excess reactant given.
The key to recognizing which reactant is the limiting reactant is based on a mole-mass or mass-mass calculation: whichever reactant gives the lesser amount of product is the limiting reactant. What we need to do is determine an amount of one product (either moles or mass) assuming all of each reactant reacts. Whichever reactant gives the least amount of that particular product is the limiting reactant. It does not matter which product we use, as long as we use the same one each time. It does not matter whether we determine the number of moles or grams of that product; however, we will see shortly that knowing the final mass of product can be useful.
As an example, consider the balanced equation
\[\ce{4 C2H3Br3 + 11 O2 \rightarrow 8 CO2 + 6 H2O + 6 Br2} \nonumber \]
What is the limiting reactant if 76.4 grams of \(\ce{C_2H_3Br_3}\) reacted with 49.1 grams of \(\ce{O_2}\)?
Solution
Using Approach 1:
Step 1: Balance the chemical equation.
The equation is already balanced with the relationship
4 mol \(\ce{C2H3Br3}\) to 11 mol \(\ce{O2}\) to 6 mol \(\ce{H2O}\) to 6 mol \(\ce{Br}\)
Step 2: Convert all given information into moles.
\[\mathrm{76.4\:\cancel{g \:C_2H_3Br_3} \times \dfrac{1\: mol \:C_2H_3Br_3}{266.72\:\cancel{g \:C_2H_3B_3}} = 0.286\: mol \: C_2H_3Br_3} \nonumber \]
\[\mathrm{49.1\: \cancel{g\: O_2} \times \dfrac{1\: mol\: O_2}{32.00\:\cancel{g\: O_2}} = 1.53\: mol\: O_2} \nonumber \]
Step 3: Calculate the mole ratio from the given information. Compare the calculated ratio to the actual ratio.
Assuming that all of the oxygen is used up,
\(\mathrm{1.53 \: \cancel{mol O_2} \times \dfrac{4 \: mol C_2H_3Br_3 }{11 \: \cancel{mol O_2}}}\) = 0.556 mol C2H3Br3 are required.
Because 0.556 moles of C2H3Br3 required > 0.286 moles of C2H3Br3 available, C2H3Br3 is the limiting reactant.
Using Approach 2:
Step 1: Balance the chemical equation.
The equation is already balanced with the relationship
4 mol C2H3Br3 to 11 mol O2 to 6 mol H2O to 6 mol Br2
Step 2 and Step 3: Convert mass to moles and stoichiometry.
\[\mathrm{76.4\:\cancel{g\: C_2H_3Br_3} \times \dfrac{1\: \cancel{mol\: C_2H_3Br_3}}{266.72\:\cancel{g\: C_2H_3Br_3}} \times \dfrac{8\: \cancel{mol\: CO_2}}{4\: \cancel{mol\: C_2H_3Br_3}} \times \dfrac{44.01\:g\: CO_2}{1\: \cancel{mol\: CO_2}} = 25.2\:g\: CO_2} \nonumber \]
\[\mathrm{49.1\: \cancel{ g\: O_2} \times \dfrac{1\: \cancel{ mol\: O_2}}{32.00\: \cancel{ g\: O_2}} \times \dfrac{8\: \cancel{ mol\: CO_2}}{11\: \cancel{ mol\: O_2}} \times \dfrac{44.01\:g\: CO_2}{1\: \cancel{ mol\: CO_2}} = 49.1\:g\: CO_2} \nonumber \]
Step 4: The reactant that produces a smaller amount of product is the limiting reactant.
Therefore, by either method, \(\ce{C2H3Br3}\) is the limiting reactant.
For example, in the reaction of magnesium metal and oxygen, calculate the mass of magnesium oxide that can be produced if 2.40 g \(Mg\) reacts with 10.0 g \(O_2\). Also determine the amount of excess reactant. \(\ce{MgO}\) is the only product in the reaction.
Solution
Following Approach 1:
Step 1: Balance the chemical equation.
2 Mg (s) + O2 (g) → 2 MgO (s)
The balanced equation provides the relationship of 2 mol Mg to 1 mol O2 to 2 mol MgO
Step 2 and Step 3: Convert mass to moles and stoichiometry.
\[\mathrm{2.40\:\cancel{g\: Mg }\times \dfrac{1\: \cancel{mol\: Mg}}{24.31\:\cancel{g\: Mg}} \times \dfrac{2\: \cancel{mol\: MgO}}{2\: \cancel{mol\: Mg}} \times \dfrac{40.31\:g\: MgO}{1\: \cancel{mol\: MgO}} = 3.98\:g\: MgO} \nonumber \]
\[\mathrm{10.0\:\cancel{g\: O_2}\times \dfrac{1\: \cancel{mol\: O_2}}{32.00\:\cancel{g\: O_2}} \times \dfrac{2\: \cancel{mol\: MgO}}{1\:\cancel{ mol\: O_2}} \times \dfrac{40.31\:g\: MgO}{1\: \cancel{mol\: MgO}} = 25.2\: g\: MgO} \nonumber \]
Step 4: The reactant that produces a smaller amount of product is the limiting reactant.
Mg produces less MgO than does O2 (3.98 g MgO vs. 25.2 g MgO), therefore Mg is the limiting reactant in this reaction.
Step 5: The reactant that produces a larger amount of product is the excess reactant.
O2 produces more amount of MgO than Mg (25.2g MgO vs. 3.98 MgO), therefore O2 is the excess reactant in this reaction.
Step 6: Find the amount of remaining excess reactant by subtracting the mass of the excess reactant consumed from the total mass of excess reactant given.
Mass of excess reactant calculated using the limiting reactant:
\[\mathrm{2.40\: \cancel{ g\: Mg }\times \dfrac{1\: \cancel{ mol\: Mg}}{24.31\: \cancel{ g\: Mg}} \times \dfrac{1\: \cancel{ mol\: O_2}}{2\: \cancel{ mol\: Mg}} \times \dfrac{32.00\:g\: O_2}{1\: \cancel{ mol\: O_2}} = 1.58\:g\: O_2} \nonumber \]
OR
Mass of excess reactant calculated using the mass of the product:
\[\mathrm{3.98\: \cancel{ g\: MgO }\times \dfrac{1\: \cancel{ mol\: MgO}}{40.31\: \cancel{ g\: MgO}} \times \dfrac{1\: \cancel{ mol\: O_2}}{2\: \cancel{ mol\: MgO}} \times \dfrac{32.0\:g\: O_2}{1\: \cancel{ mol\: O_2}} = 1.58\:g\: O_2} \nonumber \]
Mass of total excess reactant given – mass of excess reactant consumed in the reaction:
10.0g O2 - (available) 1.58g O2 (used) = 8.42g O2 (excess)
Therefore, O2 is in excess.
What is the limiting reactant if 78.0 grams of Na2O2 were reacted with 29.4 grams of H2O? The unbalanced chemical equation is \[\ce{Na2O2 (s) + H2O (l) → NaOH (aq) + H2O2 (l)} \nonumber \]
Solution
| Steps for Problem Solving- The Product Method | Example \(\PageIndex{1}\) |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." |
Given: 78.0 grams of Na2O2 29.4 g H2O Find: limiting reactant |
| List other known quantities. |
1 mol Na2O2= 77.96 g/mol Since the amount of product in grams is not required, only the molar mass of the reactants is needed. |
| Balance the equation. |
Na2O2 (s) + 2H2O (l) → 2NaOH (aq) + H2O2 (l) The balanced equation provides the relationship of 1 mol Na2O2 to 2 mol H2O 2mol NaOH to 1 mol H2O2 |
| Prepare a concept map and use the proper conversion factor. |
Because the question only asks for the limiting reactant, we can perform two mass-mole calculations and determine which amount is less. |
| Cancel units and calculate. |
\[\mathrm{78.0\:g\: Na_2O_2 \times \dfrac{1\: mol\: Na_2O_2}{77.96\:g\: Na_2O_2} \times \dfrac{2\: mol\: NaOH}{1\: mol\: Na_2O_2} \times \dfrac{40\:g\: NaOH}{1\: mol\: NaOH} = 2.00\:mol\: NaOH} \nonumber \] \[\mathrm{29.4\:g\: H_2O \times \dfrac{1\: mol\: H_2O}{18.02\:g\: H_2O} \times \dfrac{2\: mol\: NaOH}{2\: mol\: Na_2O_2} \times \dfrac{40\:g\: NaOH}{1\: mol\: NaOH} = 1.63\:mol\: NaOH} \nonumber \] Therefore, H2O is the limiting reactant. |
Think about your result.
A 5.00 g quantity of \(\ce{Rb}\) is combined with 3.44 g of \(\ce{MgCl2}\) according to this chemical reaction: \[2R b(s) + MgCl_2(s) → Mg(s) + 2RbCl(s) \nonumber \]
What mass of \(\ce{Mg}\) is formed, and what mass of remaining reactant is left over?
Solution
| Steps for Problem Solving- The Product Method | Example \(\PageIndex{2}\) |
|---|---|
| Steps for Problem Solving |
A 5.00 g quantity of Rb is combined with 3.44 g of MgCl2 according to this chemical reaction: \[2Rb(s) + MgCl_2(s) → Mg(s) + 2RbCl(s) \nonumber \] What mass of Mg is formed, and what mass of remaining reactant is left over? |
| Identify the "given" information and what the problem is asking you to "find." |
Given: 5.00g Rb, 2.44g MgCl2 |
| List other known quantities. |
|
| Prepare concept maps and use the proper conversion factor. |
Find mass Mg formed based on mass of Rb Find mass of Mg formed based on mass of MgCl2 Use limiting reactant to determine amount of excess reactant consumed |
| Cancel units and calculate. |
Because the question asks what mass of magnesium is formed, we can perform two mass-mass calculations and determine which amount is less. \[5.00\cancel{g\, Rb}\times \dfrac{1\cancel{mol\, Rb}}{85.47\cancel{g\, Rb}}\times \dfrac{1\cancel{mol\, Mg}}{2\cancel{mol\, Rb}}\times \dfrac{24.31\, g\, Mg}{\cancel{1\, mol\, Mg}}=0.711\, g\, Mg \nonumber \] \[3.44\cancel{g\, MgCl_{2}}\times \dfrac{1\cancel{mol\, MgCl_{2}}}{95.21\cancel{g\, MgCl_{2}}}\times \dfrac{1\cancel{mol\, Mg}}{1\cancel{mol\, MgCl_{2}}}\times \dfrac{24.31\, g\, Mg}{\cancel{1\, mol\, Mg}}=0.878\, g\, Mg \nonumber \] The 0.711 g of Mg is the lesser quantity, so the associated reactant—5.00 g of Rb—is the limiting reactant. To determine how much of the other reactant is left, we have to do one more mass-mass calculation to determine what mass of MgCl2 reacted with the 5.00 g of Rb, and then subtract the amount reacted from the original amount. \[5.00\cancel{g\, Rb}\times \dfrac{1\cancel{mol\, Rb}}{85.47\cancel{g\, Rb}}\times \dfrac{1\cancel{mol\, MgCl_{2}}}{2\cancel{mol\, Rb}}\times \dfrac{95.21\, g\, MgCl_{2}}{\cancel{1\, mol\, MgCl_{2}}}=2.78\, g\, MgCl_{2}\: \: reacted \nonumber \] Because we started with 3.44 g of MgCl2, we have 3.44 g MgCl2 − 2.78 g MgCl2 reacted = 0.66 g MgCl2 left |
| Think about your result. | It usually is not possible to determine the limiting reactant using just the initial masses, as the reagents have different molar masses and coefficients. |
Given the initial amounts listed, what is the limiting reactant, and what is the mass of the leftover reactant?
\[\underbrace{22.7\, g}_{MgO(s)}+\underbrace{17.9\, g}_{H_2S}\rightarrow MgS(s)+H_{2}O(l) \nonumber \]
- Answer
- H2S is the limiting reagent; 1.5 g of MgO are left over.

