9.2: Light- Electromagnetic Radiation
- Page ID
- 48628
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Define the terms wavelength and frequency with respect to wave-form energy.
- State the relationship between wavelength and frequency with respect to electromagnetic radiation.
During the summer, almost everyone enjoys going to the beach. Beach-goers can swim, have picnics, and work on their tans. But if a person gets too much sun, they can burn. A particular set of solar wavelengths are especially harmful to the skin. This portion of the solar spectrum is known as UV B, with wavelengths of \(280\)-\(320 \: \text{nm}\). Sunscreens are effective in protecting skin against both the immediate skin damage and the long-term possibility of skin cancer.
Waves
Waves are characterized by their repetitive motion. Imagine a toy boat riding the waves in a wave pool. As the water wave passes under the boat, it moves up and down in a regular and repeated fashion. While the wave travels horizontally, the boat only travels vertically up and down. The figure below shows two examples of waves.
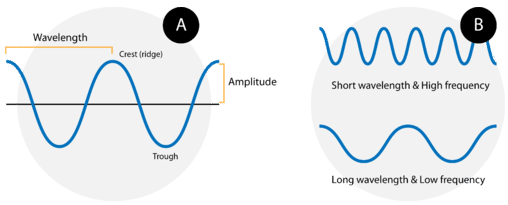
A wave cycle consists of one complete wave—starting at the zero point, going up to a wave crest, going back down to a wave trough, and back to the zero point again. The wavelength of a wave is the distance between any two corresponding points on adjacent waves. It is easiest to visualize the wavelength of a wave as the distance from one wave crest to the next. In an equation, wavelength is represented by the Greek letter lambda \(\left( \lambda \right)\). Depending on the type of wave, wavelength can be measured in meters, centimeters, or nanometers \(\left( 1 \: \text{m} = 10^9 \: \text{nm} \right)\). The frequency, represented by the Greek letter nu \(\left( \nu \right)\), is the number of waves that pass a certain point in a specified amount of time. Typically, frequency is measured in units of cycles per second or waves per second. One wave per second is also called a Hertz \(\left( \text{Hz} \right)\) and in SI units is a reciprocal second \(\left( \text{s}^{-1} \right)\).
Figure B above shows an important relationship between the wavelength and frequency of a wave. The top wave clearly has a shorter wavelength than the second wave. However, if you picture yourself at a stationary point watching these waves pass by, more waves of the first kind would pass by in a given amount of time. Thus the frequency of the first wave is greater than that of the second wave. Wavelength and frequency are therefore inversely related. As the wavelength of a wave increases, its frequency decreases. The equation that relates the two is:
\[c = \lambda \nu \nonumber \]
The variable \(c\) is the speed of light. For the relationship to hold mathematically, if the speed of light is used in \(\text{m/s}\), the wavelength must be in meters and the frequency in Hertz.
The color orange within the visible light spectrum has a wavelength of about \(620 \: \text{nm}\). What is the frequency of orange light?
Solution
| Steps for Problem Solving | Example \(\PageIndex{1}\) |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." |
Given :
Find: Frequency (Hz) |
| List other known quantities. | \(1 \: \text{m} = 10^9 \: \text{nm}\) |
| Identify steps to get the final answer. |
1.Convert the wavelength to \(\text{m}\). 2. Apply the equation \(c = \lambda \nu\) and solve for frequency. Dividing both sides of the equation by \(\lambda\) yields: \(\nu = \dfrac{c}{\lambda}\) |
| Cancel units and calculate. |
\(620 \: \text{nm} \times \left( \dfrac{1 \: \text{m}}{10^9 \: \text{nm}} \right) = 6.20 \times 10^{-7} \: \text{m}\) \(\nu = \dfrac{c}{\lambda} = \dfrac{3.0 \times 10^8 \: \text{m/s}}{6.20 \times 10^{-7}} = 4.8 \times 10^{14} \: \text{Hz}\) |
| Think about your result. | The value for the frequency falls within the range for visible light. |
What is the wavelength of light if its frequency is 1.55 × 1010 s−1?
- Answer
- 0.0194 m, or 19.4 mm
Summary
All waves can be defined in terms of their frequency and intensity. \(c = \lambda \nu\) expresses the relationship between wavelength and frequency.

