2.8: Units Raised to a Power
- Page ID
- 86017
Skills to Develop
- To convert a value reported in one unit raised to a power of 10 to a corresponding value in a different unit raised to the same power of 10 using conversion factors.
Conversion factors for area and volume can also be produced by the dimensional analysis method. Just remember that if a quantity is raised to a power of 10 both the number and the unit must be raised to the same power of 10. For example to convert \(1500 \: \text{cm}^2\) to \(\text{m}^2\), we need to start with the relationship between centimeter and meter. We know that 1 cm = 10-2 m or 100 cm =1 m, but since we are given the quantity in 1500 cm2, then we have to use the relationship:
\[1\, cm^2 = (10^{-2}\, m)^2 = 10^{-4}\, m^2\]
CONCEPT MAP
CALCULATION
\[1500 \: \cancel{\text{cm}}^2 \times \left( \frac{10^{-2} \: \text{m}}{1 \: \cancel{\text{cm}}} \right)^2 = 0.15 \: \text{m}^2\]
or
\[1500 \: \cancel{\text{cm}}^2 \times \left( \frac{1 \: \text{m}}{100 \: \cancel{\text{cm}}} \right)^2 = 0.15 \: \text{m}^2\]
or
\[1500 \: \cancel{\text{cm}}^2 \times \frac{1 \: \text{m}^2}{10,000 \: \cancel{\text{cm}^2}} = 0.15 \: \text{m}^2\]
Example \(\PageIndex{1}\): Volume of a sphere
What is the volume of a sphere (radius 4.30 inches) in cubic cm (cm3)?
Solution
|
Steps for Problem Solving |
What is the volume of a sphere (radius 4.30 inches) in cubic cm (cm3)? |
| Identify the "given” information and what the problem is asking you to "find." |
Given: radius = 4.30 in Find: cm3 (volume) |
| Determine other known quantities |
Volume of a sphere: V = \(\frac{4}{3} \times \pi \times r^3 \) = \(\frac{4}{3} \times 3.1416 \times (4.3\underline{0}in)^3 \) = \(33\underline{3}.04 in^3\) |
|
Prepare a concept map |
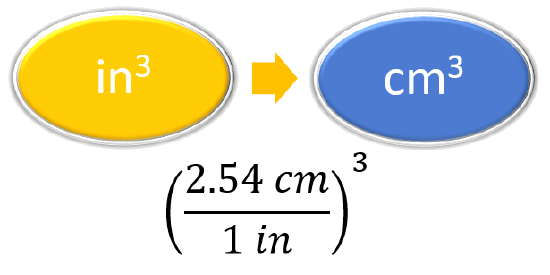 |
|
Calculate |
\(33\underline{3}.04 \cancel{in^3} \left(\frac{2.54cm}{1 \cancel{in}}\right)^3 = 5.46 \times10^3 cm^3\) |
|
Think about your result |
A centimeter is a smaller unit than an inch, so the answer in cubic centimeter is larger than the given value in cubic inch. |
Exercise \(\PageIndex{1}\)
Lake Tahoe has a surface area of 191 square miles. What is the area in square km (km2)?
- Answer:
- 495 km2

