6.5: Chemical Formulas as Conversion Factors

Last updated
Save as PDF

Page ID: 48602

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Learning Objectives

Use chemical formulas as conversion factors.

Figure \(\PageIndex{1}\) shows that we need 2 hydrogen atoms and 1 oxygen atom to make one water molecule. If we want to make two water molecules, we will need 4 hydrogen atoms and 2 oxygen atoms. If we want to make five molecules of water, we need 10 hydrogen atoms and 5 oxygen atoms. The ratio of atoms we will need to make any number of water molecules is the same: 2 hydrogen atoms to 1 oxygen atom.

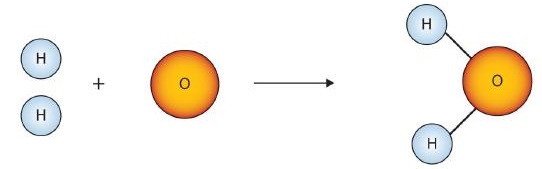
In water, the ratio of hydrogen atoms to oxygen atoms is 2 to 1. — Figure \(\PageIndex{1}\) Water Molecules. The ratio of hydrogen atoms to oxygen atoms used to make water molecules is always 2:1, no matter how many water molecules are being made.

Using formulas to indicate how many atoms of each element we have in a substance, we can relate the number of moles of molecules to the number of moles of atoms. For example, in 1 mol of water (H₂O) we can construct the relationships given in (Table \(\PageIndex{1}\)).

Table \(\PageIndex{1}\): Molecular Relationships for Water
1 Molecule of \(H_2O\) Has	1 Mol of \(H_2O\) Has	Molecular Relationships
2 H atoms	2 mol of H atoms	\(\mathrm{\dfrac{2\: mol\: H\: atoms}{1\: mol\: H_2O\: molecules}}\) or \(\mathrm{\dfrac{1\: mol\: H_2O\: molecules}{2\: mol\: H\: atoms}}\)
1 O atom	1 mol of O atoms	\(\mathrm{\dfrac{1\: mol\: O\: atoms}{1\: mol\: H_2O\: molecules}}\) or \(\mathrm{\dfrac{1\: mol\: H_2O\: molecules}{1\: mol\: O\: atoms}}\)

The Mole is big

A mole represents a very large number! The number 602,214,129,000,000,000,000,000 looks about twice as long as a trillion, which means it’s about a trillion trillion.

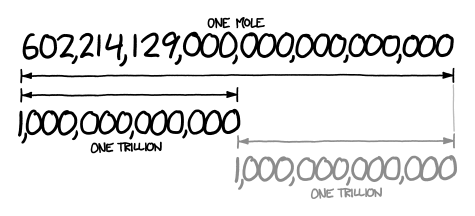
(CC BY-SA NC; what if? [what-if.xkcd.com]).

A trillion trillion kilograms is how much a planet weighs. If 1 mol of quarters were stacked in a column, it could stretch back and forth between Earth and the sun 6.8 billion times.

Table \(\PageIndex{2}\): Molecular and Mass Relationships for Ethanol
1 Molecule of \(C_2H_6O\) Has	1 Mol of \(C_2H_6O\) Has	Molecular and Mass Relationships
2 C atoms	2 mol of C atoms	\(\mathrm{\dfrac{2\: mol\: C\: atoms}{1\: mol\: C_2H_6O\: molecules}}\) or \(\mathrm{\dfrac{1\: mol\: C_2H_6O\: molecules}{2\: mol\: C\: atoms}}\)
6 H atoms	6 mol of H atoms	\(\mathrm{\dfrac{6\: mol\: H\: atoms}{1\: mol\: C_2H_6O\: molecules}}\) or \(\mathrm{\dfrac{1\: mol\: C_2H_6O\: molecules}{6\: mol\: H\: atoms}}\)
1 O atom	1 mol of O atoms	\(\mathrm{\dfrac{1\: mol\: O\: atoms}{1\: mol\: C_2H_6O\: molecules}}\) or \(\mathrm{\dfrac{1\: mol\: C_2H_6O\: molecules}{1\: mol\: O\: atoms}}\)
2 (12.01 amu) C 24.02 amu C	2 (12.01 g) C 24.02 g C	\(\mathrm{\dfrac{24.02\: g\: C\: }{1\: mol\: C_2H_6O\: molecules}}\) or \(\mathrm{\dfrac{1\: mol\: C_2H_6O\: molecules}{24.02\: g\: C\: }}\)
6 (1.008 amu) H 6.048 amu H	6 (1.008 g) H 6.048 g H	\(\mathrm{\dfrac{6.048\: g\: H\: }{1\: mol\: C_2H_6O\: molecules}}\) or \(\mathrm{\dfrac{1\: mol\: C_2H_6O\: molecules}{6.048\: g\: H\: }}\)
1 (16.00 amu) O 16.00 amu O	1 (16.00 g) O 16.00 g O	\(\mathrm{\dfrac{16.00\: g\: O\: }{1\: mol\: C_2H_6O\: molecules}}\) or \(\mathrm{\dfrac{1\: mol\: C_2H_6O\: molecules}{16.00\: g\: O\: }}\)

The following example illustrates how we can use the relationships in Table \(\PageIndex{2}\) as conversion factors.

Example \(\PageIndex{1}\): Ethanol

If a sample consists of 2.5 mol of ethanol (C₂H₆O), how many moles of carbon atoms does it have?

Solution

Solutions to Example 6.5.1
Steps for Problem Solving	If a sample consists of 2.5 mol of ethanol (C₂H₆O), how many moles of carbon atoms does it have?
Identify the "given" information and what the problem is asking you to "find."	Given: 2.5 mol C₂H₆O Find: mol C atoms
List other known quantities.	1 mol C₂H₆O = 2 mol C
Prepare a concept map and use the proper conversion factor.
Cancel units and calculate.	Note how the unit mol C₂H₆O molecules cancels algebraically. \(\mathrm{2.5\: \cancel{mol\: C_2H_6O\: molecules}\times\dfrac{2\: mol\: C\: atoms}{1\: \cancel{mol\: C_2H_6O\: molecules}}=5.0\: mol\: C\: atoms}\)
Think about your result.	There are twice as many C atoms in one C₂H₆O molecule, so the final amount should be double.

Exercise \(\PageIndex{1}\)

If a sample contains 6.75 mol of Na₂SO₄, how many moles of sodium atoms, sulfur atoms, and oxygen atoms does it have?

Answer: 13.5 mol Na atoms, 6.75 mol S atoms, and 27.0 mol O atoms

The fact that 1 mol equals 6.022 × 10²³ items can also be used as a conversion factor.

Example \(\PageIndex{2}\): Oxygen Mass

Determine the mass of Oxygen in 75.0g of C₂H₆O.

Solution

Solutions to Example 6.5.2
Steps for Problem Solving	Determine the mass of Oxygen in 75.0g of C₂H₆O
Identify the "given" information and what the problem is asking you to "find."	Given: 75.0g C₂H₆O Find: g O
List other known quantities.	1 mol O = 16.0g O 1 mol C₂H₆O = 1 mol O 1 mol C₂H₆O = 46.07g C₂H₆O
Prepare a concept map and use the proper conversion factor.	The conversion factors are 1 mol C2H6O over 46.07 g C2H6O, 1 mol O over 1 mol C2H6O, and 16.00 g O over 1 mole O.
Cancel units and calculate.	\(\require{cancel}\mathrm{75.0\: \cancel{g\: C_2H_6O}\times\dfrac{1\: \cancel{mol\: C_2H_6O}}{46.07\:\cancel{g\: C_2H_6O}}\times\dfrac{1\: \cancel{mol\:O}}{1\: \cancel{mol\:C_2H_6O}}\times\dfrac{16.00\: g\: O}{1\: \cancel{mol\:O}}=26.0\: g\: O}\)
Think about your result.

Exercise \(\PageIndex{2}\)

How many molecules are present in 16.02 mol of C₄H₁₀? How many C atoms are in 16.02 mol?
How many moles of each type of atom are in 2.58 mol of Na₂SO₄?

Answer a:: 9.647 x 10²⁴ C₄H₁₀molecules and 3.859 x 10²⁵ C atoms

Answer b:: 5.16 mol Na atoms, 2.58 mol S atoms, and 10.3 mol O atoms

Summary

In any given formula, the ratio of the number of moles of molecules (or formula units) to the number of moles of atoms can be used as a conversion factor.