13.7: Solution Dilution
- Page ID
- 48672
- Explain how concentrations can be changed in the lab.
- Understand how stock solutions are used in the laboratory.
We are often concerned with how much solute is dissolved in a given amount of solution. We will begin our discussion of solution concentration with two related and relative terms: dilute and concentrated.
- A dilute solution is one in which there is a relatively small amount of solute dissolved in the solution.
- A concentrated solution contains a relatively large amount of solute.
These two terms do not provide any quantitative information (actual numbers), but they are often useful in comparing solutions in a more general sense. These terms also do not tell us whether or not the solution is saturated or unsaturated, or whether the solution is "strong" or "weak". These last two terms will have special meanings when we discuss acids and bases, so be careful not to confuse them.
Stock Solutions
It is often necessary to have a solution with a concentration that is very precisely known. Solutions containing a precise mass of solute in a precise volume of solution are called stock (or standard) solutions. To prepare a standard solution, a piece of lab equipment called a volumetric flask should be used. These flasks range in size from 10 mL to 2000 mL and are carefully calibrated to a single volume. On the narrow stem is a calibration mark. The precise mass of solute is dissolved in a bit of the solvent, and this is added to the flask. Then, enough solvent is added to the flask until the level reaches the calibration mark.
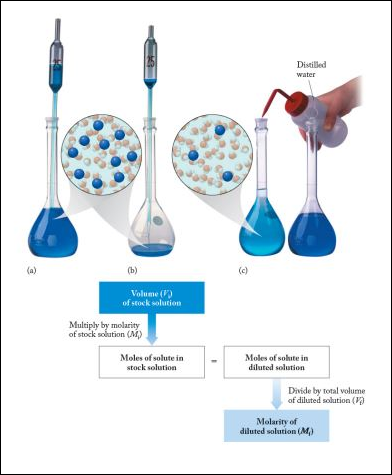
Often, it is convenient to prepare a series of solutions of known concentrations by first preparing a single stock solution, as described in the previous section. Aliquots (carefully measured volumes) of the stock solution can then be diluted to any desired volume. In other cases, it may be inconvenient to weigh a small mass of sample accurately enough to prepare a small volume of a dilute solution. Each of these situations requires that a solution be diluted to obtain the desired concentration.
Dilutions of Stock (or Standard) Solutions
Imagine we have a salt water solution with a certain concentration. That means we have a certain amount of salt (a certain mass or a certain number of moles) dissolved in a certain volume of solution. Next, we will dilute this solution. This is done by adding more water, not more salt:
 \(\rightarrow\)
\(\rightarrow\) 
Before Dilution and After Dilution
The molarity of solution 1 is
\[ M_1 = \dfrac{\text{moles}_1}{\text{liter}_1} \nonumber \]
and the molarity of solution 2 is
\[ M_2 = \dfrac{\text{moles}_2}{\text{liter}_2} \nonumber \]
rearrange the equations to find moles:
\[ \text{moles}_1 = M_1 \text{liter}_1 \nonumber \]
and
\[ \text{moles}_2 = M_2 \text{liter}_2 \nonumber \]
What stayed the same and what changed between the two solutions? By adding more water, we changed the volume of the solution. Doing so also changed its concentration. However, the number of moles of solute did not change. So,
\[moles_1 = moles_2 \nonumber \]
Therefore
\[ \boxed{M_1V_1= M_2V_2 } \label{diluteEq} \]
where
- \(M_1\) and \(M_2\) are the concentrations of the original and diluted solutions
- \(V_1\) and \(V_2\) are the volumes of the two solutions
Preparing dilutions is a common activity in the chemistry lab and elsewhere. Once you understand the above relationship, the calculations are simple.
Suppose that you have \(100. \: \text{mL}\) of a \(2.0 \: \text{M}\) solution of \(\ce{HCl}\). You dilute the solution by adding enough water to make the solution volume \(500. \: \text{mL}\). The new molarity can easily be calculated by using the above equation and solving for \(M_2\).
\[M_2 = \dfrac{M_1 \times V_1}{V_2} = \dfrac{2.0 \: \text{M} \times 100. \: \text{mL}}{500. \: \text{mL}} = 0.40 \: \text{M} \: \ce{HCl} \nonumber \]
The solution has been diluted by one-fifth since the new volume is five times as great as the original volume. Consequently, the molarity is one-fifth of its original value.
Another common dilution problem involves calculating what amount of a highly concentrated solution is required to make a desired quantity of solution of lesser concentration. The highly concentrated solution is typically referred to as the stock solution.
Nitric acid \(\left( \ce{HNO_3} \right)\) is a powerful and corrosive acid. When ordered from a chemical supply company, its molarity is \(16 \: \text{M}\). How much of the stock solution of nitric acid needs to be used to make \(8.00 \: \text{L}\) of a \(0.50 \: \text{M}\) solution?
Solution
| Steps for Problem Solving | |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." |
Given: M1, Stock \(\ce{HNO_3} = 16 \: \text{M}\) \(V_2 = 8.00 \: \text{L}\) \(M_2 = 0.50 \: \text{M}\) Find: Volume stock \(\ce{HNO_3} \left( V_1 \right) = ? \: \text{L}\) |
| List other known quantities. | none |
| Plan the problem. |
First, rearrange the equation algebraically to solve for \(V_1\). \[V_1 = \dfrac{M_2 \times V_2}{M_1} \nonumber \] |
| Calculate and cancel units. |
Now substitute the known quantities into the equation and solve. \[V_1 = \dfrac{0.50 \: \text{M} \times 8.00 \: \text{L}}{16 \: \text{M}} = 0.25 \: \text{L}\] |
| Think about your result. | \( 0.25 \: \text{L} \: (250 \: \text{mL})\) of the stock \(\ce{HNO_3}\) needs to be diluted with water to a final volume of \(8.00 \: \text{L}\). The dilution is by a factor of 32 to go from \(16 \: \text{M}\) to \(0.5 \: \text{M}\). |
A 0.885 M solution of KBr with an initial volume of 76.5 mL has more water added until its concentration is 0.500 M. What is the new volume of the solution?
Answer
135.4 mL
Note that the calculated volume will have the same dimensions as the input volume, and dimensional analysis tells us that in this case we don't need to convert to liters, since L cancels when we divide M (mol/L) by M (mol/L).
Diluting and Mixing Solutions
|
How to Dilute a Solution by CarolinaBiological |
 |
|---|

