7.9: Oxidation–Reduction Reactions
- Page ID
- 48617
- Define oxidation and reduction.
- Assign oxidation numbers to atoms in simple compounds.
- Recognize a reaction as an oxidation-reduction reaction.
In the course of a chemical reaction between a metal and a nonmetal, electrons are transferred from the metal atoms to the nonmetal atoms. For example, when zinc metal is mixed with sulfur and heated, the compound zinc sulfide is produced. Two valence electrons from each zinc atom are transferred to each sulfur atom.

Since the zinc is losing electrons in the reaction, it is being oxidized. The sulfur is gaining electrons and is thus being reduced. An oxidation-reduction reaction is a reaction that involves the full or partial transfer of electrons from one reactant to another. Oxidation is the full or partial loss of electrons or the gain of oxygen. Reduction is the full or partial gain of electrons or the loss of oxygen. A redox reaction is another term for an oxidation-reduction reaction.
Each of these processes can be shown in a separate equation called a half-reaction. A half-reaction is an equation that shows either the oxidation or the reduction reaction that occurs during a redox reaction.
\[ \underbrace{\ce{Zn→Zn^{2+}+2e^{−}}}_{\text{Oxidation}} \label{7.9.1} \]
\[ \underbrace{\ce{S+ 2 e^{−} → S^{2−}}}_ {\text{Reduction}} \label{7.9.2} \]
It is important to remember that the two half-reactions occur simultaneously. The resulting ions that are formed are then attracted to one another in an ionic bond.
Another example of an oxidation-reduction reaction involving electron transfer is the well-known combination of metallic sodium and chlorine gas to form sodium chloride:
\[\ce{2Na+Cl_2→2NaCl} \label{7.9.3} \]
The half reactions are as follows:
\[ \underbrace{\ce{2Na→2Na^{+} + 2e^{−}}}_{\text{Oxidation}} \label{7.941} \]
\[ \underbrace{\ce{Cl_2 +2e^{−} → 2Cl^{−}}}_ {\text{Reduction}} \label{7.9.5} \]
We will concern ourselves with the balancing of these equations at another time.
Oxidation Numbers
Redox reactions require that we keep track of the electrons assigned to each atom in a chemical reaction. How do we do that? We use oxidation numbers to keep track of electrons in atoms. Oxidation numbers are assigned to atoms based on four rules. Oxidation numbers are not necessarily equal to the charge on the atom (although sometimes they can be); we must keep the concepts of charge and oxidation numbers separate.
The rules for assigning oxidation numbers to atoms are as follows:
1. Atoms in their elemental state are assigned an oxidation number of 0.
In H2, both H atoms have an oxidation number of 0.
2. Atoms in monatomic (i.e., one-atom) ions are assigned an oxidation number equal to their charge. Oxidation numbers are usually written with the sign first, then the magnitude, to differentiate them from charges.
In MgCl2, magnesium has an oxidation number of +2, while chlorine has an oxidation number of −1.
3. In compounds, fluorine is assigned a −1 oxidation number; oxygen is usually assigned a −2 oxidation number (except in peroxide compounds [where it is −1] and in binary compounds with fluorine [where it is positive]); and hydrogen is usually assigned a +1 oxidation number [except when it exists as the hydride ion (H−), in which case rule 2 prevails].
In H2O, the H atoms each have an oxidation number of +1, while the O atom has an oxidation number of −2, even though hydrogen and oxygen do not exist as ions in this compound (rule 3). By contrast, by rule 3, each H atom in hydrogen peroxide (H2O2) has an oxidation number of +1, while each O atom has an oxidation number of −1.
4. In compounds, all other atoms are assigned an oxidation number so that the sum of the oxidation numbers on all the atoms in the species equals the charge on the species (which is zero if the species is neutral).
In SO2, each O atom has an oxidation number of −2; for the sum of the oxidation numbers to equal the charge on the species (which is zero), the S atom is assigned an oxidation number of +4. Does this mean that the sulfur atom has a 4+ charge on it? No, it means only that the S atom is assigned a +4 oxidation number by our rules of apportioning electrons among the atoms in a compound.
Assign oxidation numbers to the atoms in each substance.
- Cl2
- GeO2
- Ca(NO3)2
Solution
- Cl2 is the elemental form of chlorine. Rule 1 states that each atom has an oxidation number of 0.
- By rule 3, oxygen is normally assigned an oxidation number of −2. For the sum of the oxidation numbers to equal the charge on the species (zero), the Ge atom is assigned an oxidation number of +4.
- Ca(NO3)2 can be separated into two parts: the Ca2+ ion and the NO3− ion. Considering these separately, the Ca2+ ion has an oxidation number of +2 by rule 2. Now consider the NO3− ion. Oxygen is assigned an oxidation number of −2, and there are three of them. According to rule 4, the sum of the oxidation numbers on all atoms must equal the charge on the species, so we have the simple algebraic equation \[x + 3(−2) = −1 \nonumber \]
where x is the oxidation number of the N atom and the −1 represents the charge on the species. Evaluating for x,
\[x + (−6) = −1x = +5 \nonumber \]Thus the oxidation number on the N atom in the NO3− ion is +5.
Assign oxidation numbers to the atoms in the following:
- H3PO4
- MgO
- Answer a
- H: +1; O: −2; P: +5
- Answer b
- Mg: +2, O: −2
All redox reactions occur with a simultaneous change in the oxidation numbers of some atoms. At least two elements must change their oxidation numbers. When an oxidation number of an atom is increased in the course of a redox reaction, that atom is being oxidized. When an oxidation number of an atom is decreased in the course of a redox reaction, that atom is being reduced. Thus oxidation and reduction can also be defined in terms of increasing or decreasing oxidation numbers, respectively.
Identify what is being oxidized and reduced in the following redox reaction.
\[\ce{2Na + Br2 → 2NaBr} \nonumber \]
Solution
Both reactants are the elemental forms of their atoms, so the Na and Br atoms have oxidation numbers of 0. In the ionic product, the Na+ ions have an oxidation number of +1, while the Br− ions have an oxidation number of −1.
\[2\underset{0}{Na}+\underset{0}{Br_{2}}\rightarrow 2\underset{+1 -1}{NaBr} \nonumber \]
Sodium is increasing its oxidation number from 0 to +1, so it is being oxidized; bromine is decreasing its oxidation number from 0 to −1, so it is being reduced:
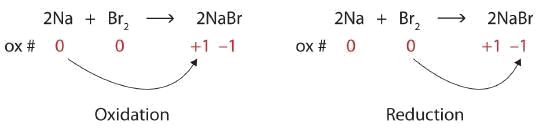
Because oxidation numbers are changing, this is a redox reaction. The total number of electrons being lost by sodium (two, one lost from each Na atom) is gained by bromine (two, one gained for each Br atom).
Identify what is being oxidized and reduced in this redox reaction.\[C + O_2 → CO_2 \nonumber \]
- Answer
- C is being oxidized from 0 to +4; O is being reduced from 0 to −2
Oxidation reactions can become quite complex, as attested by the following redox reaction:
\[6H^{+}(aq)+2\underset{+7}{MnO_{4}^{-}}(aq)+5\underset{-1}{H_{2}O_{2}}(l)\rightarrow 2\underset{+2}{Mn^{2+}}(aq)+5\underset{0}{O_{2}}(g)+8H_{2}O(l) \nonumber \]
To demonstrate that this is a redox reaction, the oxidation numbers of the species being oxidized and reduced are listed; can you determine what is being oxidized and what is being reduced? This is also an example of a net ionic reaction; spectator ions that do not change oxidation numbers are not displayed in the equation. Eventually, we will need to learn techniques for writing correct (i.e., balanced) redox reactions.
Combustion Reactions
A combustion reaction is a reaction in which a substance reacts with oxygen gas, releasing energy in the form of light and heat. Combustion reactions must involve \(\ce{O_2}\) as one reactant. The combustion of hydrogen gas produces water vapor.
\[2 \ce{H_2} \left( g \right) + \ce{O_2} \left( g \right) \rightarrow 2 \ce{H_2O} \left( g \right) \label{water} \]
Notice that this reaction also qualifies as a combination reaction.

The Hindenberg was a hydrogen-filled airship that suffered an accident upon its attempted landing in New Jersey in 1937. The hydrogen immediately combusted in a huge fireball, destroying the airship and killing 36 people. The chemical reaction was a simple one: hydrogen combining with oxygen to produce water (Equation \ref{water}).
Many combustion reactions occur with a hydrocarbon, a compound made up solely of carbon and hydrogen. The products of the combustion of hydrocarbons are carbon dioxide and water. Many hydrocarbons are used as fuel because their combustion releases very large amounts of heat energy. Propane \(\left( \ce{C_3H_8} \right)\) is a gaseous hydrocarbon that is commonly used as the fuel source in gas grills.
\[\ce{C_3H_8} \left( g \right) + 5 \ce{O_2} \left( g \right) \rightarrow 3 \ce{CO_2} \left( g \right) + 4 \ce{H_2O} \left( g \right) \nonumber \]
Ethanol can be used as a fuel source in an alcohol lamp. The formula for ethanol is \(\ce{C_2H_5OH}\). Write the balanced equation for the combustion of ethanol.
Solution
| Steps | Example Solution |
|---|---|
| Write the unbalanced reaction. |
\(\ce{C_2H_5OH} \left( l \right) + \ce{O_2} \left( g \right) \rightarrow \ce{CO_2} \left( g \right) + \ce{H_2O} \left( g \right)\) Ethanol and atmospheric oxygen are the reactants. As with a hydrocarbon, the products of the combustion of an alcohol are carbon dioxide and water. |
| Balance the equation. | \(\ce{C_2H_5OH} \left( l \right) + 3 \ce{O_2} \left( g \right) \rightarrow 2 \ce{CO_2} \left( g \right) + 3 \ce{H_2O} \left( g \right)\) |
| Think about your result. | Combustion reactions must have oxygen as a reactant. Note that the water produced is in the gas state, rather than the liquid state, because of the high temperatures that accompany a combustion reaction. |
Write the balanced equation for the combustion of hexane, C6H14
- Answer
- \[\ce{2C6H14 (ℓ) + 19O2(g) → 12CO2(g) + 14H2O(ℓ)} \nonumber \]

