2.9: Density
- Page ID
- 86018
- Define density.
- Use density as a conversion factor.
Density (\(\rho\)) is a physical property found by dividing the mass of an object by its volume. Regardless of the sample size, density is always constant. For example, the density of a pure sample of tungsten is always 19.25 grams per cubic centimeter. This means that whether you have one gram or one kilogram of the sample, the density will never vary. The equation, as we already know, is as follows:
\[\text{Density}=\dfrac{\text{Mass}}{\text{Volume}} \nonumber \]
or just
\[\rho =\dfrac{m}{V} \label{eq2} \]
Based on this equation, it's clear that density can, and does, vary from element to element and substance to substance due to differences in the relationship of mass and volume. Pure water, for example, has a density of 0.998 g/cm3 at 25° C. The average densities of some common substances are in Table \(\PageIndex{1}\). Notice that corn oil has a lower mass to volume ratio than water. This means that when added to water, corn oil will “float.”
| Substance | Density at 25°C (g/cm3) |
|---|---|
| blood | 1.035 |
| body fat | 0.918 |
| whole milk | 1.030 |
| corn oil | 0.922 |
| mayonnaise | 0.910 |
| honey | 1.420 |
Density can be measured for all substances—solids, liquids and gases. For solids and liquids, density is often reported using the units of g/cm3. Densities of gases, which are significantly lower than the densities of solids and liquids, are often given using units of g/L.
Calculate the density of a 30.2 mL sample of ethyl alcohol with a mass of 23.71002 g
Solution
This is a direct application of Equation \ref{eq2}:
\[\rho = \dfrac{23.71002\,g}{30.2\,mL} = 0.785\, g/mL \nonumber \]
- Find the density (in kg/L) of a sample that has a volume of 36.5 L and a mass of 10.0 kg.
- If you have a 2.130 mL sample of acetic acid with mass 0.002234 kg, what is the density in kg/L?
- Answer a
- \(0.274 \,kg/L\)
- Answer b
- \(1.049 \,kg/L\)
Density as a Conversion Factor
Conversion factors can also be constructed for converting between different kinds of units. For example, density can be used to convert between the mass and the volume of a substance. Consider mercury, which is a liquid at room temperature and has a density of 13.6 g/mL. The density tells us that 13.6 g of mercury have a volume of 1 mL. We can write that relationship as follows:
13.6 g mercury = 1 mL mercury
This relationship can be used to construct two conversion factors:
\[\dfrac{13.6\:g}{1\:mL} = 1 \nonumber \]
and
\[\dfrac{1\:mL}{13.6\:g} = 1 \nonumber \]
Which one do we use? It depends, as usual, on the units we need to cancel and introduce. For example, suppose we want to know the mass of 2.0 mL of mercury. We would use the conversion factor that has milliliters on the bottom (so that the milliliter unit cancels) and grams on top, so that our final answer has a unit of mass:
\[\mathrm{2.0\:\cancel{mL}\times\dfrac{13.6\:g}{1\:\cancel{mL}}=27.2\:g=27\:g} \nonumber \]
In the last step, we limit our final answer to two significant figures because the volume quantity has only two significant figures; the 1 in the volume unit is considered an exact number, so it does not affect the number of significant figures. The other conversion factor would be useful if we were given a mass and asked to find volume, as the following example illustrates.
Density can be used as a conversion factor between mass and volume.
A mercury thermometer for measuring a patient’s temperature contains 0.750 g of mercury. What is the volume of this mass of mercury?
Solution
| Steps for Problem Solving | Unit Conversion |
|---|---|
| Identify the "given" information and what the problem is asking you to "find." |
Given: 0.750 g Find: mL |
| List other known quantities. | 13.6 g/mL (density of mercury) |
| Prepare a concept map. | 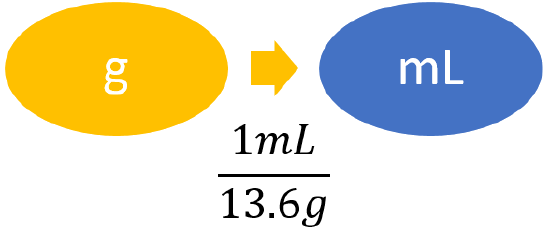 |
| Calculate. |
\[ 0.750 \; \cancel{\rm{g}} \times \dfrac{1\; \rm{mL}}{13.6 \; \cancel{\rm{g}}} = 0.055147 ... \; \rm{mL} \approx 0.0551\; \rm{mL} \nonumber \] We have limited the final answer to three significant figures. |
What is the volume of 100.0 g of air if its density is 1.3 g/L?
- Answer
- \(77 \, L\)
Summary
- Density is defined as the mass of an object divided by its volume.
- Density can be used as a conversion factor between mass and volume.

