Introduction to NMR
- Page ID
- 1834
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Nuclear Magnetic Resonance (NMR) is a nuclei (Nuclear) specific spectroscopy that has far reaching applications throughout the physical sciences and industry. NMR uses a large magnet (Magnetic) to probe the intrinsic spin properties of atomic nuclei. Like all spectroscopies, NMR uses a component of electromagnetic radiation (radio frequency waves) to promote transitions between nuclear energy levels (Resonance). Most chemists use NMR for structure determination of small molecules.
Introduction
In 1946, NMR was co-discovered by Purcell, Pound and Torrey of Harvard University and Bloch, Hansen and Packard of Stanford University. The discovery first came about when it was noticed that magnetic nuclei, such as 1H and 31P (read: proton and Phosphorus 31) were able to absorb radio frequency energy when placed in a magnetic field of a strength that was specific to the nucleus. Upon absorption, the nuclei begin to resonate and different atoms within a molecule resonated at different frequencies. This observation allowed a detailed analysis of the structure of a molecule. Since then, NMR has been applied to solids, liquids and gasses, kinetic and structural studies, resulting in 6 Nobel prizes being awarded in the field of NMR.
Spin and Magnetic Properties
The nucleus consists of elementary particles called neutrons and protons, which contain an intrinsic property called spin. Like electrons, the spin of a nucleus can be described using quantum numbers of I for the spin and m for the spin in a magnetic field. Atomic nuclei with even numbers of protons and neutrons have zero spin and all the other atoms with odd numbers have a non-zero spin. Furthermore, all molecules with a non-zero spin have a magnetic moment, \(\mu\), given by
\[\mu=\gamma I\]
where \(\gamma\) is the gyromagnetic ratio, a proportionality constant between the magnetic dipole moment and the angular momentum, specific to each nucleus (Table 1).
| Nuclei | Spin | Gyromagetic Ratio (MHz/T) | Natural Abundance (%) |
|---|---|---|---|
| 1H | 1/2 | 42.576 | 99.9985 |
| 13C | 1/2 | 10.705 | 1.07 |
| 31P | 1/2 | 17.235 | 100 |
| 27Al | 5/2 | 11.103 | 100 |
| 23Na | 3/2 | 11.262 | 100 |
| 7Li | 3/2 | 16.546 | 92.41 |
|
29Si |
1/2 | -8.465 | 4.68 |
| 17O | 5/2 | 5.772 | 0.038 |
| 15N | 1/2 | -4.361 | 0.368 |
The magnetic moment of the nucleus forces the nucleus to behave as a tiny bar magnet. In the absence of an external magnetic field, each magnet is randomly oriented. During the NMR experiment the sample is placed in an external magnetic field, \(B_0\), which forces the bar magnets to align with (low energy) or against (high energy) the \(B_0\). During the NMR experiment, a spin flip of the magnets occurs, requiring an exact quanta of energy. To understand this rather abstract concept it is useful to consider the NMR experiment using the nuclear energy levels.

Nuclear Energy Levels
As mentioned above, an exact quanta of energy must be used to induce the spin flip or transition. For any m, there are 2m+1 energy levels. For a spin 1/2 nucleus, there are only two energy levels, the low energy level occupied by the spins which aligned with \(B_0\) and the high energy level occupied by spins aligned against \(B_0\). Each energy level is given by
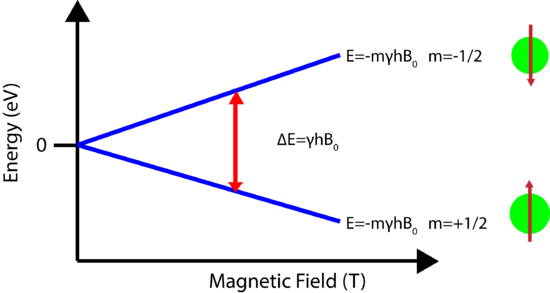
\[E=-m\hbar \gamma B_0\]
where \(m\) is the magnetic quantum number, in this case +/- 1/2. The energy levels for \(m>1/2\), known as quadrupolar nuclei, are more complex and information regarding them can be found here.
The energy difference between the energy levels is then
\[\Delta E=\hbar \gamma B_0\]
where \(\hbar\) is Planks constant.
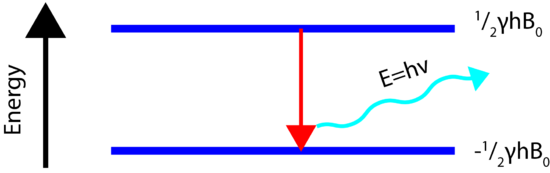
A schematic showing how the energy levels are arranged for a spin=1/2 nucleus is shown below. Note how the strength of the magnetic field plays a large role in the energy level difference. In the absence of an applied field the nuclear energy levels are degenerate. The splitting of the degenerate energy level due to the presence of a magnetic field in known as Zeeman Splitting.
Energy Transitions (Spin Flip)
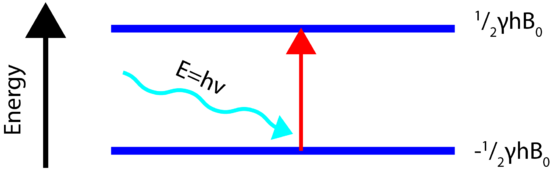
In order for the NMR experiment to work, a spin flip between the energy levels must occur. The energy difference between the two states corresponds to the energy of the electromagnetic radiation that causes the nuclei to change their energy levels. For most NMR spectrometers, \(B_0\) is on the order of Tesla (T) while \(\gamma\) is on the order of \(10^7\). Consequently, the electromagnetic radiation required is on the order of 100's of MHz and even GHz. The energy of a photon is represented by
\[E=h\nu\]
and thus the frequency necessary for absorption to occur is represented as:
\[\nu=\dfrac{\gamma B_0}{2\pi}\]
For the beginner, the NMR experiment measures the resonant frequency that causes a spin flip. For the more advanced NMR users, the sections on NMR detection and Larmor frequency should be consulted.
Nuclear Shielding
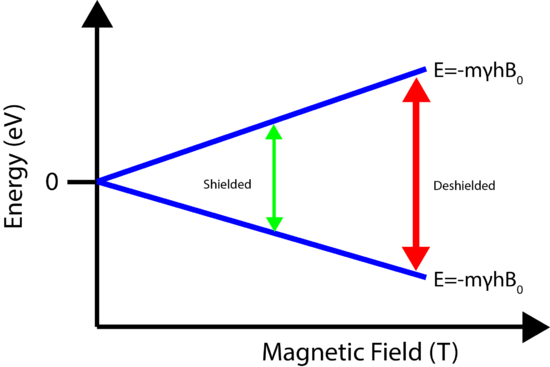
The power of NMR is based on the concept of nuclear shielding, which allows for structural assignments. Every atom is surrounded by electrons, which orbit the nucleus. Charged particles moving in a loop will create a magnetic field which is felt by the nucleus. Therefore the local electronic environment surrounding the nucleus will slightly change the magnetic field experienced by the nucleus, which in turn will cause slight changes in the energy levels! This is known as shielding. Nuclei that experience different magnetic fields due to the local electronic interactions are known as inequivalent nuclei. The change in the energy levels requires a different frequency to excite the spin flip, which as will be seen below, creates a new peak in the NMR spectrum. The shielding allows for structural determination of molecules.
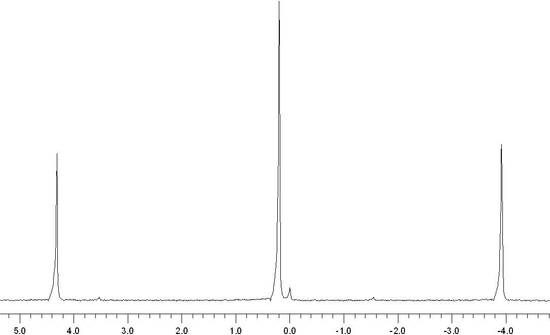
The shielding of the nucleus allows for chemically inequivalent environments to be determined by Fourier Transforming the NMR signal. The result is a spectrum, shown below, that consists of a set of peaks in which each peak corresponds to a distinct chemical environment. The area underneath the peak is directly proportional to the number of nuclei in that chemical environment. Additional details about the structure manifest themselves in the form of different NMR interactions, each altering the NMR spectrum in a distinct manner. The x-axis of an NMR spectrum is given in parts per million (ppm) and the relation to shielding is explained here.
Relaxation
Relaxation refers to the phenomenon of nuclei returning to their thermodynamically stable states after being excited to higher energy levels. The energy absorbed when a transition from a lower energy level to a high energy level occurs is released when the opposite happens. This can be a fairly complex process based on different timescales of the relaxation. The two most common types of relaxation are spin lattice relaxation (T1) and spin spin relaxation (T2). A more complex treatment of relaxation is given elsewhere.
To understand relaxation, the entire sample must be considered. By placing the nuclei in an external magnetic field, the nuclei create a bulk magnetization along the z-axis. The spins of the nuclei are also coherent. The NMR signal may be detected as long as the spins are coherent with one another. The NMR experiment moves the bulk magnetization from the z-axis to the x-y plane, where it is detected.
- Spin-Lattice Relaxation (\(T_1\)): T1 is the time it takes for the 37% of bulk magnetization to recovery along Z-axis from the x-y plane. The more efficient the relaxation process, the smaller relaxation time (T1) value you will get. In solids, since motions between molecules are limited, the relaxation time (T1) values are large. Spin-lattice relaxation measurements are usually carried out by pulse methods.
- Spin-Spin Relaxation (\(T_2\)): T2 is the time it takes for the spins to lose coherence with one another. T2 can either be shorter or equal to T1.
Applications
The two major areas where NMR has proven to be of critical importance is in the fields of medicine and chemistry, with new applications being developed daily
Nuclear magnetic resonance imaging, better known as magnetic resonance imaging (MRI) is an important medical diagnostic tool used to study the function and structure of the human body. It provides detailed images of any part of the body, especially soft tissue, in all possible planes and has been used in the areas of cardiovascular, neurological, musculoskeletal and oncological imaging. Unlike other alternatives, such as computed tomography (CT), it does not used ionized radiation and hence is very safe to administer.

In many laboratories today, chemists use nuclear magnetic resonance to determine structures of important chemical and biological compounds. In NMR spectra, different peaks give information about different atoms in a molecule according specific chemical environments and bonding between atoms. The most common isotopes used to detect NMR signals are 1H and 13C but there are many others, such as 2H, 3He, 15N, 19F, etc., that are also in use.
NMR has also proven to be very useful in other area such as environmental testing, petroleum industry, process control, earth’s field NMR and magnetometers. Non-destructive testing saves a lot of money for expensive biological samples and can be used again if more trials need to be run. The petroleum industry uses NMR equipment to measure porosity of different rocks and permeability of different underground fluids. Magnetometers are used to measure the various magnetic fields that are relevant to one’s study.
Problems
- Calculate the magnetic field, B0 that corresponds to a precession frequency of 600 MHz for 1H.
- What is the field strength (in tesla) needed to generate a 1H frequency of 500 MHz?
- How do spin-spin relaxation and spin-lattice relaxation differ from each other?
- The 1H NMR spectrum of toluene shows that it has two peaks because of methyl and aromatic protons recorded at 60 MHz and 1.41 T. Given this information, what would be the magnetic field at 400 MHz?
- What is the difference between 13C and 1H NMR?
Solutions
- B0= 14.1 T.
- Using the equation used in problem 1 and solving it for B0we get a field strength of 11.74 T.
- Look under relaxation.
- Since we know that the NMR frequency is directly proportional to the magnetic strength, we calculate the magnetic field at 400 MHz: B0 = (400 MHz/60MHz) x 1.41 T = 9.40 T
- Look under applications.
References
- Atta-ur-Rahman. Nuclear Magnetic Resonance. New York: Springer-Verlag, 1986.
- Freeman, Ray. Magnetic Resonance in Chemistry and Medicine. New York: Oxford University Press, 2003.
- Lambert, Joseph B and Eugene P Mazzola. Nuclear Magnetic Resonance Spectroscopy: An Introduction to Princliples, Applications, and Experimental Methods. Upper Saddle River: Pearson Education, 2004.
- Chang, Raymond. Physical Chemistry for the Biosciences. University Science Books, 2005

