Relaxation
- Page ID
- 1829
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Relaxation in NMR is a fundamental concept which describes the coherence loss of the magnetization in the x-y plane and the recovery of relaxation along the z-axis. One can easily imagine that in the absence of any other effects, the magnetization in the x-y plane will recover along the z-axis as the external magnetic field forces the spins to align with it. This is known as T1 relaxation. The loss of coherence of the magnetization in the x-y plane is due to spins "forgetting" their orientation with respect to the bulk magnetization. This is known as T2 relaxation. There are many factors that contribute to the relaxation processes. This page will examine the different types of relaxation at a basic level. For those interested in a deeper discussion please see article on T1 and T2 relaxation.
T1 Relaxation
T1 relaxation, also known as spin lattice or longitudinal relaxation is the time constant used to describe when ~63% of the magnetization has recovered to equilibrium. The T1 of a given spin is dictated by field fluctuations (both magnetic and electric) that occur in the sample. Consequently, T1 measurements can tell us important information regarding inter and intra molecular dynamics of the system. Several factor may cause this alternating field: molecular motion, J-Coupling, Dipolar Coupling, Chemical Shift Anisotropy, and quadrupole-phonon interactions.
We can also look at relaxation from the energy level standpoint. Initially, we have a Boltzmann distribution of spins in the (For I=1/2) in two energy levels, with the lower energy level slightly more populated than the higher energy level. After a pulse these spin populations are inverted and now the higher energy level has more spins in it. Eventually, these spins will go back to their lower energy state due to relaxation. The timescale on which this occurs is T1.
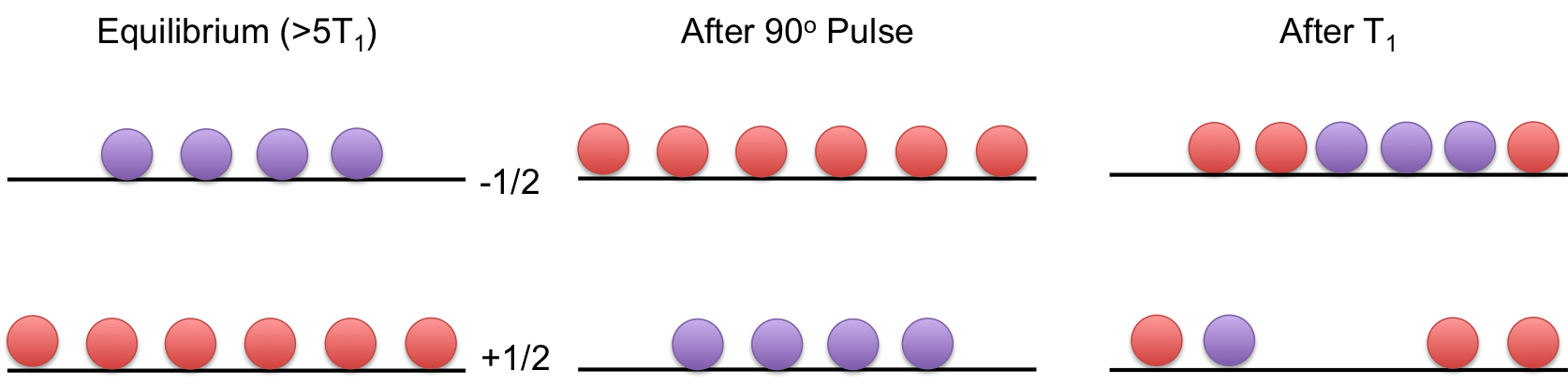
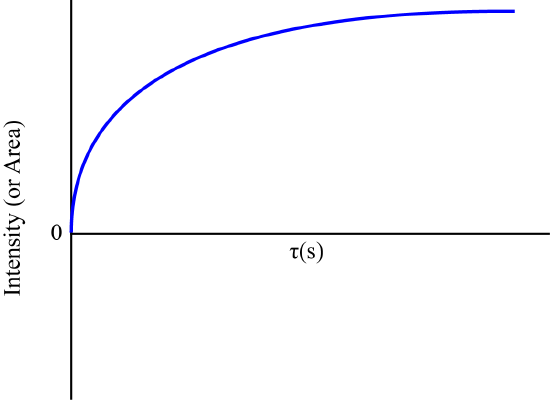
From the Bloch Equations, we know that magnetization is along the Z-axis is
\[M_z=M_0(1-\exp\frac{-t}{T_1})\]
T1\(\rho\) Relaxation
T1\(\rho\) is the relaxation of the magnetization during a spin lock. This becomes particularly important in the cross-polarization.
T2 Relaxation
T2 relaxation is also known as spin-spin or transverse relaxation. T2 relaxation involves energy transfer between interacting spins via dipole and exchange interactions. Spin-spin relaxation energy is transferred to a neighboring nucleus. The time constant for this process is called the spin-spin relaxation time (T2). The relaxation rate is proportional to the concentration of paramagnetic ions in the sample. This mechanism is largely temperature independent. T2 values are generally much less dependent on field strength, B, than T1 values.
In the process of relaxation, the component of magnetization in xy-plane will become zero as M0 returns to z-axis. Time constant T2 is used here to describe spin-spin relaxation with the following function. This process involves energy changing between the spin-active and their adjacent nuclei.
\[M_{xy}=M_{xy0}exp\frac{-t}{T_2}\]
T2* Relaxation
In an ideal NMR spectrometer, the external magnetic field is completely homogeneous. However, all magnets have small inhomegneities in them. Consequently, nuclei experience different magnetic fields which changes the precessional frequency of each nucleus. The change in Larmor frequency results in dphasing in the transverse plane and is known as T2*

Magnetic Field Dependence
So far, we have only described what the relaxation parameters are, but have largely omitted the equations that give us the results. All elaxation measurements are based on the idea of a correlation time, tc. The correlation time is based on the environment that the spin is in. For \(T_1\) relaxation, the correlation time must be on the order of the larmor frequency of the nucleus, while the correlation time for the for \(T_2\) must be on the order of the inverse of the linewidth to make effects. The correlation time are random fluctuations in the magnetic field that couple to the nucleus. The equations that govern \(T_1\) and \(T_2\) are given below with no additional proof..
\[\begin{align*} \frac{1}{T_{1}} &=C \left(\frac{t_{c}}{1+w^{2}t_{c}^{2}}+\frac{2t_{c}}{1+4w^{2}t_{c}^{2}}\right) \\[4pt] \frac{1}{T_{2}} &=3Ct_{c} \left(\frac{2}{\pi}\right)^\frac{3}{2}+\frac{1}{2} \end{align*}\]
where \(w\) is the Larmor frequency, and \(C\) is a constant that contains temperature and frequency independent terms and defined as....
References
- Levitt, M. H., Spin Dynamics, Wiley
- Bloembergen, E.M. Purcell, R.V. Pound "Relaxation Effects in Nuclear Magnetic Resonance Absorption" Physical Review 1948, 73, 679-746
- www.uthgsbsmedphys.org/GS02-0032/documents/RelaxationMechanisms.pdf
- http://chem.ch.huji.ac.il/nmr/techniques/other/t1t2/t1t2.html
Problems
1. Derive why only 63% of spins have recovered to equilibrium after T1
2. Explain the differences between T1, T1/(/rho/),T2, and T2*.


