Chemical Shift (Shielding)
- Page ID
- 1824
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The chemical shift in NMR is extremely important, as it gives vital information about the local structure surrounding the nucleus of interest. For a majority of scientists, the chemical shift is used exlusivley to determine structure, especially in organic systems. Additional information may be gained by examining the anisotropy of the chemical shift. This section will be devoted to looking at chemical shift from a mathematical standpoint including a full treatment of the chemical shift tensor and the relation to the NMR lineshape.
Shielding and Chemical Shift
As electrons orbit the nucleus, the slightly alter the magnetic field that the nucleus experineces, which slightly changes the difference between the energy levels which gives the resulting spectra. However, these changes are from a select reference and therefore are relative. The resulting change in the energy levels is on the order of Hz, while the Zeeman interaction is on the order of MHz. Thus we can develop a scale based on the relative changes in the energy levels.
Beginning with the equation for Zeeman splitting
\[\Delta E=-\gamma \hbar B_0\]
the effect of shielding \(\sigma\), results in
\[\Delta E=-\gamma \hbar (1-\sigma) B_0\]
in which the quantitiy \((1-\sigma)B_0\) is known as the effective field experineced by the nucleus \(B_{eff}\). Relating the change in energy to a frequency using
\[E=h\nu\]
The value for the shielding is based off the resonant frequency for some reference sample, such as tetrmethylsilane (TMS), \(\sigma_{ref}\). This can cause confusion as the strength of the magnetic field dictates the exact frequency is field dependent. To make the shielding constant between magnetic fields it becomes customary to diving by the resonant frequency of the given nucleus. This gives values on the order of \(10^{-6}\) or ppm. This value is known as chemical shift, \(\delta\), and is given by
\[\delta=10^6(\sigma_{ref}-\sigma_{sample})\]
Chemical Shift Tensor
Consider a system consisting of a single spin 1/2 nucleus; I. \(\hat{H}_{CS}\) may then be represented as
\[\hat{H}_{cs}=-\dfrac{\gamma {h} \hat{I} \sigma B_0}{2\pi}\]
where \(\gamma\) is the gyromagnetic ratio, h is Plank's constant, \(\hat{I}\) is the spin operator, and \(\sigma\) is the chemical shift tensor. This tensor may be represented as
\[\sigma= \begin{pmatrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{yx} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma_{zz} \end{pmatrix}\]
The principle axis system (PAS), denoted by axes XPAS, YPAS, ZPAS,represented in the figure below. The PAS is the x, y, and z coordinates with respect to the nucleus whereas X, Y, and Z of the rotating frame are defined with B0 along the +Z direction. The chemical shift tensor describes the electric field surrounding the nucleus with the principle components of the tensor; \(\sigma_{xx}\), \(\sigma_{yy}\), \(\sigma_{zz}\).
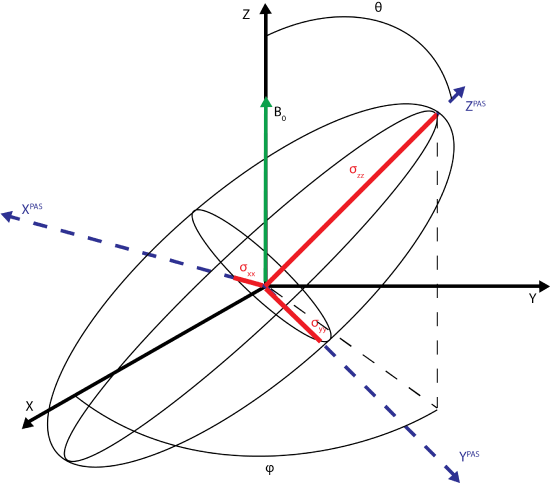
In a solid, the sample is not a single spin oriented along B0. Rather, the sample contains orientations sampling all directions in all 3 dimensions. Each magnetic moment of the system can be related for its PAS to the Z axis by an angle, \(\theta\), and its position in the x y plane given by angle \(\phi\). The magnetization experienced at the nucleus on the basis of the PAS is given by
\[B_0^{PAS}=(sin\theta cos\phi, sin\theta sin\phi, cos\theta)\].
The chemical shift, \(\omega_{cs}\), is then
\[\omega_{cs}=-\omega_0(\sigma_{xx} sin^2\theta cos^2\phi+\sigma_{yy} sin^2\theta sin^2\phi+\sigma_{zz} cos^2\theta)\],
which reduces to
\[\omega_{cs}=-\omega_0\sigma_{iso}-\dfrac{1}{2} \omega_0 \Delta[3cos^2\theta-1+\eta sin^2\theta cos2\phi]\].
\(-\omega_0 \sigma_{iso}\) is the isotropic frequency, \(\omega_{iso}=\dfrac{\nu_{iso}}{2\pi}\), routinely observed in liquid spectra.
Chemical Shift Anisotropy (CSA)
If a polycrystalline sample is then placed in a spectrometer, a lineshape similar to these may be observed:
This is due to asymmetry of the local electronic environment surrounding the nucleus. If the electronic cloud were symmetric then \(\sigma_{xx}=\sigma_{yy}=\sigma_{zz}\) and \(\Delta\) and \(\eta\) would be zero leaving only the isotropic peak. Note how broad this pattern is when compared to liquid spectra! CSA is not a large factor in liquids becasue rapid molecular tumbling averages the CSA during the experimental timescale. The above patterns can be deconstructed into the principle components of the chemical shift tensor, as indicated on the figure. This is especially useful as NMR directly correlates to the immediate local electronic structure surrounding the nucleus probed. Take for example a compound which has \(\sigma_{xx}=\sigma_{yy}\), which is said to be axially symmetric and \(\eta=0\). It is immediately obvious that there is symmetry about the nucleus which is reflected in the static lineshape (black line in above figure).
CSA Conventions
There are three major conventions people use to describe the CSA tensor. They are outlined below and once should always keep in mind the difference between shielding and chemical shift scales.
IUPAC Convention
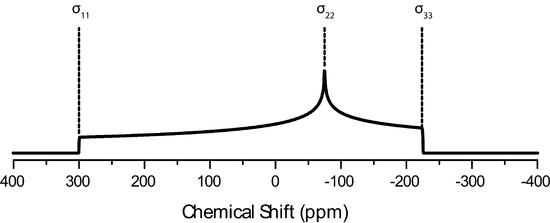
The IUPAC convention describes the CSA tensor by three values, called principle components of the CSA tensor, \(\delta_{11}, \delta_{22}, \delta_{33}\). These values follow the following magnitude
\[\delta_{11} \geqslant \delta_{22} \geqslant \delta_{33}\].
The average value or these is then the isotropic chemical shift.
\[\delta_{iso}=\dfrac{\delta_{11}+\delta_{22}+\delta_{33}}{3}\]
Herzfeld Berger Convention
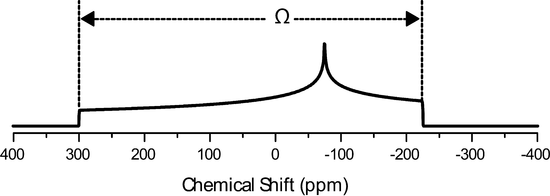
The Herzfeld Berger convention uses the IUPAC definition of the principle components, but they are represented using a different notation, the span, \(\Omega\), and the skew, \(\kappa\). They are defined as follows:
\[\delta_{iso}=\dfrac{\delta_{11}+\delta_{22}+\delta_{33}}{3}\]
\[\Omega=\delta_{11}-\delta_{33}\]
\[\kappa=\dfrac{3(\delta_{22}-\delta_{iso})}{\Omega}\]
\(\Omega\) will always be larger than or equal to 0 and \(\kappa\) will range from -1 to 1
Haeberlen Convention
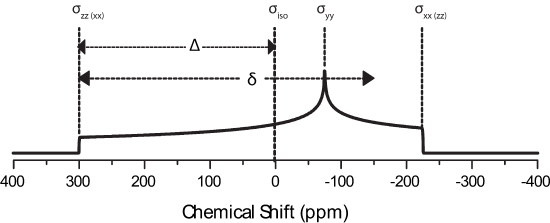
The Haberlen convention uses different combinations of the principle components to describe the CSA. They are
\[|\delta_{zz}-\delta_{iso}| \geqslant |\delta_{xx}-\delta_{iso}| \geqslant |\delta_{yy}-\delta_{iso}|\]
\[\delta_{iso}=\dfrac{\delta_{11}+\delta_{22}+\delta_{33}}{3}\]
\[\Delta=\delta_{zz}-\delta_{iso}\]
\[\delta=\dfrac{3\Delta}{2}\]
\[\eta=\dfrac{\delta_{xx}-\delta_{yy}}{\delta_{zz}-\delta_{iso}}\]
Conversion Between Conventions
Converting between the standard and Haeberlen convention is often needed to compare values of the CSA. There are two cases, one in which \(\Delta>0\) and when \(\Delta<0\). When \(\Delta>0\)
\[\delta_{11}=\delta_{iso}+\Delta\]
\[\delta_{22}=\delta_{iso}-\dfrac{\Delta(1-\eta)}{2}\]
\[\delta_{33}=\delta_{iso}-\dfrac{\Delta(1+\eta)}{2}\]
When \(\Delta>0\)
\[\delta_{33}=\delta_{iso}+\Delta\]
\[\delta_{22}=\delta_{iso}-\dfrac{\Delta(1-\eta)}{2}\]
\[\delta_{11}=\delta_{iso}-\dfrac{\Delta(1+\eta)}{2}\]
Dynamics and CSA
The CSA is very sensitive to any type of motion occurring in the system. A great example of this is a liquid. Liquids only exhibit a narrow line at the isotropic chemical shift, indicating that any CSA is averaged. The average timescale of rotation for a liquid is on the order of picoseconds which is about 1 trillion times larger than the CSA . For solids the case is more interesting as increasing the temperature can give rise to molecular motion. There are two types of motion isotropic tumbling anf rotation about a fixed axis. We will consider the implications on the CSA lineshape for each case.
Isotropic Tumbling
Isotropic rotation, or isotropic tumbling motion is occurring if the molecule is rotating in all possible directions. Therefore at one time a molecules spin may be aligned with the magnetic field, and then at the next time point be oriented perpendicular to the external magnetic field. Correspondingly, we can begin to envision that the processes of isotropic tumbling closely mirrors that of chemical exchange at a site in which each orientation of the spin may be represented as a single peak.
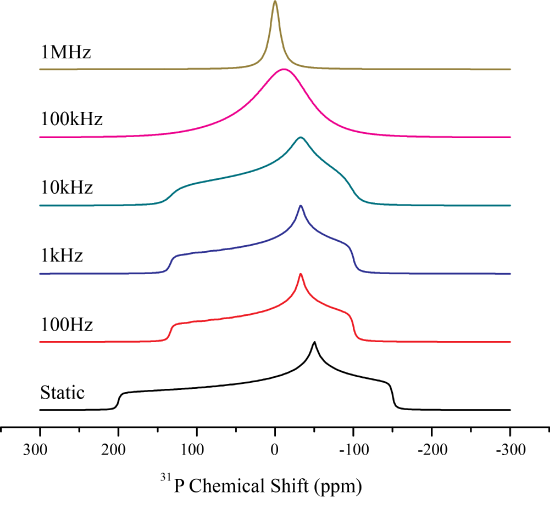
As the orientation of the spin changes, the peak position will change. Thus as the spins begin to change their orientation faster than width of the CSA, they will come to a average position, which will be the isotropic chemical shift. Mathematically this can be described as follows.
Assume there is a single crystal with a single CSA. The rotational jump is of random nature and occurs at a single rate constant, \(\kappa\). The jump is from site \(\Omega → \Omega '\) and spends an average time at any given site of \(\tau\). We also assume there is no correlation between \(\Omega\) and \(\Omega '\). Assuming a Markoff process for the time dependence, then
\[\kappa^{-1} =\tau\] .
The probability of finding a spin at orientation \(\Omega \) after a time t from an initial position of \(\Omega_0\) is
\[\dfrac{d}{dt}P(\Omega_0/\Omega,t)=\int \pi(\Omega', \Omega) P(\Omega_0/\Omega,t)d\Omega'\]
where the initial probability is then
\[P(\Omega_0/\Omega,t) = \delta(\Omega-\Omega_0)\]
and \(\delta\) is the Kroenecker Delta function and \( \pi(\Omega', \Omega) \) is a memory function that keeps the history of \(\Omega\)
As expected, as the time approaches zero then the probability approaches the initial condition, or
\[P(\Omega_0/\Omega,t) = \delta(\Omega'-\Omega_0)\]
The memory function must then be the transition probability per unit time which is
\[\pi(\Omega', \Omega)=[\dfrac{d}{dt}P(\Omega_0/\Omega,t)]_{t=0}\]
For a given time t, the probability of \(|Omega'\) rotates to \(Omega\) is given by \(kappa t\) then
\[\pi(\Omega', \Omega)= (1-\kappa t)\delta(\Omega'-\Omega) + W(\Omega)\kappa t\]
where \(W(\Omega\) is the probability of finding the molecule in orientation \(\Omega\)
then it can be shown
\[\pi(\Omega', \Omega)=[W(\Omega)-\delta(\Omega'-\Omega_0)]\]
and for a fintie number ,k, sites
\[\pi(\Omega_m, \Omega_n)=[W(\Omega_n)-\delta_{mn}]\]
The NMR spectrum will be the Fourier Transform of the FID, G(t) given by
\[G(t)=\dfrac{1}{N} \int_{\Omega} d \Omega G(t,\Omega\]
where
\[G(t,\Omega)=\sum_kQ_k\] for k sites
Assuming a line is generated for each k site at \(\omega_k\) where
\[\omega_k=\omega(\Omega_k)\]
the the equation of motion is
\[\dfrac{d}{dt}=iw(\Omega_k Q_k+\sum_j \pi(\Omega_j, Omega_k) Q_j\]
\[Q_k=Q(t,K_k)\]
The equation of motion can be expressed as a k-dimensional vector, K as
\[\dfrac{d}{dt}K=(k\omega+\pi)K
where \(\pi\) is the previously defined jump matrix and \(\omega\) is the diagonal matrix with elements
\[\omega_{kj}=\delta_{kj}\omega_{kj}\]
K can be solved to give
\[K(t)=K(0)exp[(i\omega+\pi)t]\]
\[K(0)=W=(W(\Omega_1),W(\Omega_2),W(\Omega_3),W(\Omega_n))\]
Then
\[G(t,\Omega)=W exp[(i\omega+\pi)t]\]
and the FTed spectrum is
\[I=(\omega,\Omega)Real{WA^{-1}}\]
\[A=i(\omega-\omega E)+\pi\]
Rotation about an axis
In contrast to isotropic tumbling motion, molecules may only rotate about a single fixed axis. This will ultimately change the CSA to a uniaxial pattens, once the rotation is fast enough. Depending on the \(\Delta\) and \(\eta\) the averaged pattern may even switch the sign of \(\Delta\)!
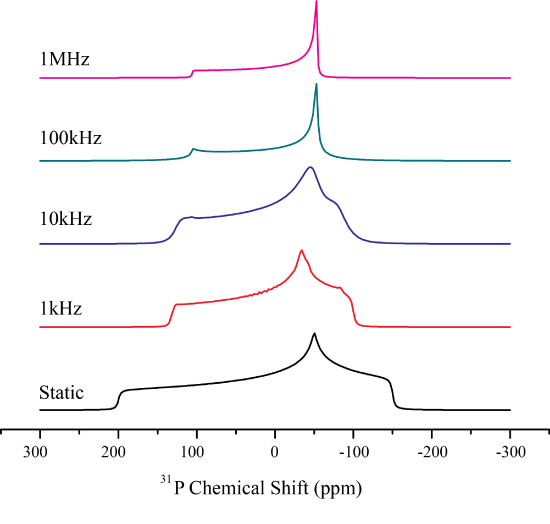
Lets explore what happens when this is the case Mathematically. It is easiest to consider the case of symmetry related jumps where a molecule performs a rotation at rate \(1/\tau_{jk}\) between symmetry equivalent positions, \(\omega_j\). The exchange between sites may then be written as
\[Ag=i\omega_1M_01\]
where A is a coupling matrix, g is the magnetization at site j, \(\omega_1\) is the RF field strength and \(M_0\) is the thermal equilibrium magnetization. The exchange matrix is a diagonal matrix with elements
\[A_{jj}=i(\omega-\omega_j)-\dfrac{1}{T_2-} \dfrac{1}{\tau_j}\]
we can the solve for g and forier transform to get the intensity ( an exercise left for the reader) to obtain the equation for the lineshape
\[I(\omega)=\int_\Omega (g(\omega,\Omega)d\Omega\]
References
- M. Mehring. High Resolution NMR spectroscopy in Solids. Springer Verlag Berlin 1976
- J. Herzfeld, A. E. Berger, J. Chem. Phys. 1980, 73, 6021
- J. Mason, Solid State Nucl. Magn. Reson. 1993, 2, 285
- U. Haeberlen, In Advances in Magnetic Resonance; Suppl. 1; J. S. Waugh, Ed.; Academic Press: New York, 1976.
- Massiot et al. Magnetic Resonance in Chemistry, 40 pp70-76 (2002)
- D.E. Wemmer et al. J.American Chemical Society. 1981, 103, 28-33
Outside Links
- Tensor Calculator http://anorganik.uni-tuebingen.de/kl...ntions/csa/csa
- Jump Frequency Spectra Generator http://weblab.mpip-mainz.mpg.de/cgi-...&version=4.5.1

