NMR - Theory
- Page ID
- 1819
Nuclear magnetic resonance plays an important role in the fields chemistry, materials science, physics and engineering. It is becoming a more and more useful method to probe the structure of molecules. The primary object of this module is to understand the fundamental concepts of NMR. It is assumed that the reader already understands the quantum numbers associated with electrons. For a more basic understanding of how NMR works, the reader is directed to the NMR introduction page.
Introduction
Nuclear magnetic resonance, NMR, is a physical phenomenon of resonance transition between magnetic energy levels, happening when atomic nuclei are immersed in an external magnetic field and applied an electromagnetic radiation with specific frequency. By detecting the absorption signals, one can acquire NMR spectrum. According to the positions, intensities and fine structure of resonance peaks, people can study the structures of molecules quantitatively. The size of molecules of interest varies from small organic molecules, to biological molecules of middle size, and even to some macromolecules such as nucleic acids and proteins. Apart from these commonly utilized applications in organic compound, NMR also play an important role in analyzing inorganic molecules, which makes NMR spectroscopy a powerful technique.
But the a major question still remains- Why does NMR work? This module will begin by developing the concept of nuclear spin then moving into a discussion about energy levels and the relative populations and the interactions of a nucleus with the magnetic field.
Nuclear Spin Origins
The concept of spin is regularly addressed in subatomic particle physics. However, to most people spin seems like an abstract concept. This is due to the fact there is no macroscopic equivalent of what spin is. However, for those people who have taken an introduction to chemistry course have seen the concept of spin in electrons. Electrons are subatomic particles which have spin intrinsic to them. The nucleus is not much different. Spin is just another form of angular momentum. The nucleus consists of protons and neutrons and neutrons and protons are comprised of subatomic particles known as quarks and gluons. The neutron has 2 quarks with a -e/3 charge and one quark with a +2e/3 charge resulting in a total charge of 0. The proton however, has 2 quarks with +2e/3 charge and only one quark with a -e/3 charge giving it a net positive charge. Both protons and neutrons are spin=1/2.
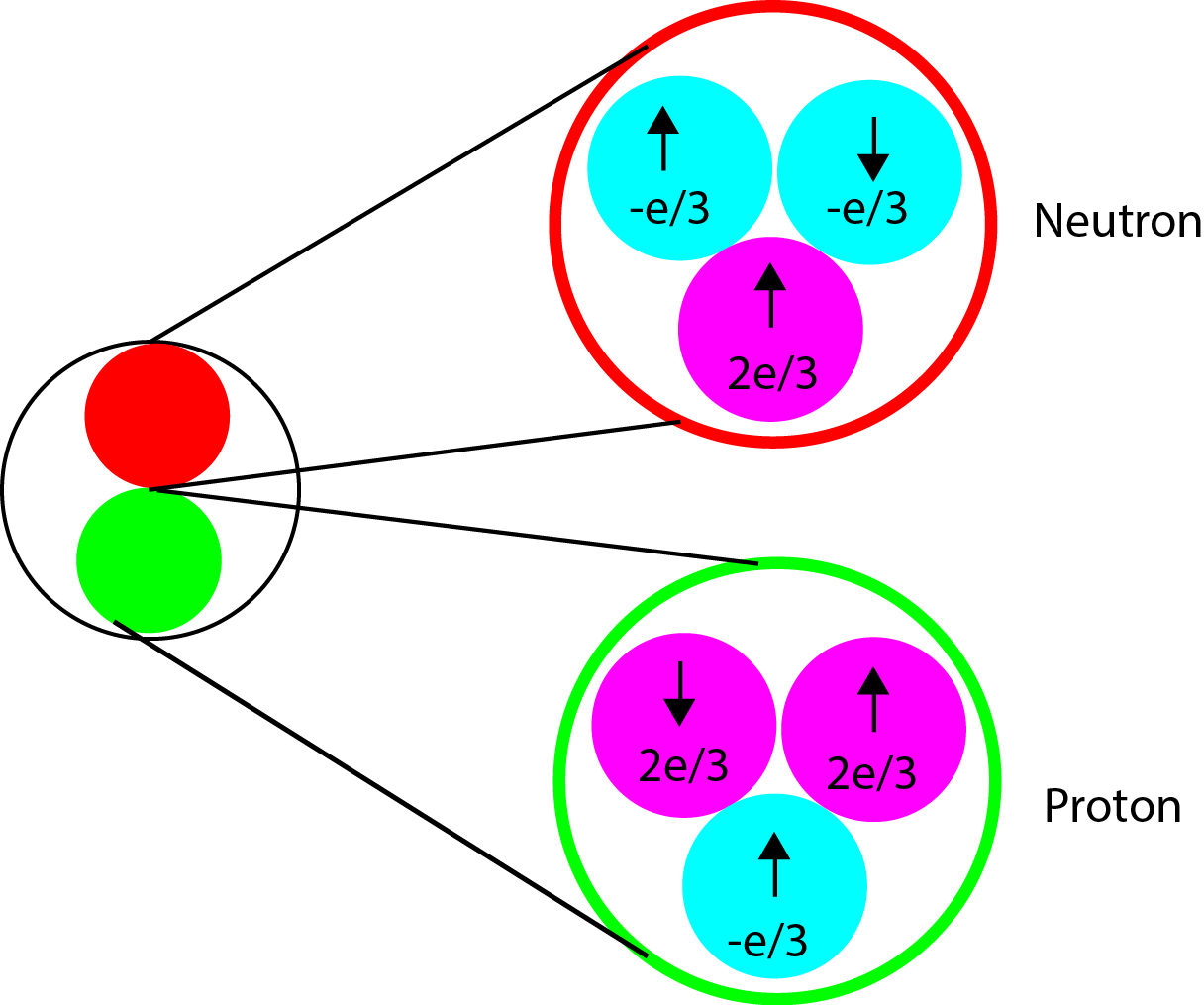
For any system consisting of n multiple parts, each with an angular momentum the total angular momentum can be described by \(J\) where
\[J=|J_1+J_2+...+J_n|, |J_1+J_2+...+J_n| -1,...|J_1-J_2-...-J_n|\]
Here are some examples using the isotopes of hydrogen
- \(^1H\) = 1 proton so J=1/2
- \(^2H\)= 1 proton and 1 neutron so \(J=1\) or 0.
For larger nuclei, it is not immediately evident what the spin should be as there are a multitude of possible values. For the remainder of the discussion we will attribute the spin of the nucleus, I, to be an intrinsic value. There are some rules that the nuclei do follow with respect to nuclear spin. They are summarized in the table below.
| Mass Number | Number of Protons | Number of Neutrons | Spin (I) | Example |
|---|---|---|---|---|
| Even | Even | Even | 0 | \(^{16}O\) |
| Odd | Odd | Integer (1,2,...) | \(^{2}H\) | |
| Odd | Even | Odd | Half-Integer (1/2, 3/2,...) | \(^{13}C\) |
| Odd | Even | Half-Integer (1/2, 3/2,...) | \(^{15}N\) |
Nuclear Spin Angular Momentum and Quantum Numbers
As mentioned above, spin is a type of angular momentum. Nuclear spin angular momentum was first reported by Pauli in 1924 and will be described here. Analogous to the angular momentum commonly encountered in electron, the angular momentum is a vector which can be described by a magnitude \(L\) and a direction, \(m\). The magnitude is given by
\[L=\hbar\sqrt{I(I+1)}\]
The projection of the vector on the z axis (arbitrarily chosen), takes on discretized values according to m, where
\[m=-I, -I+1, -I+2,...+I\]
The angular momentum along the z-axis is now
\[I_z=m\hbar\]
Pictorially, this is represented in the figure below for three values of \(I\).
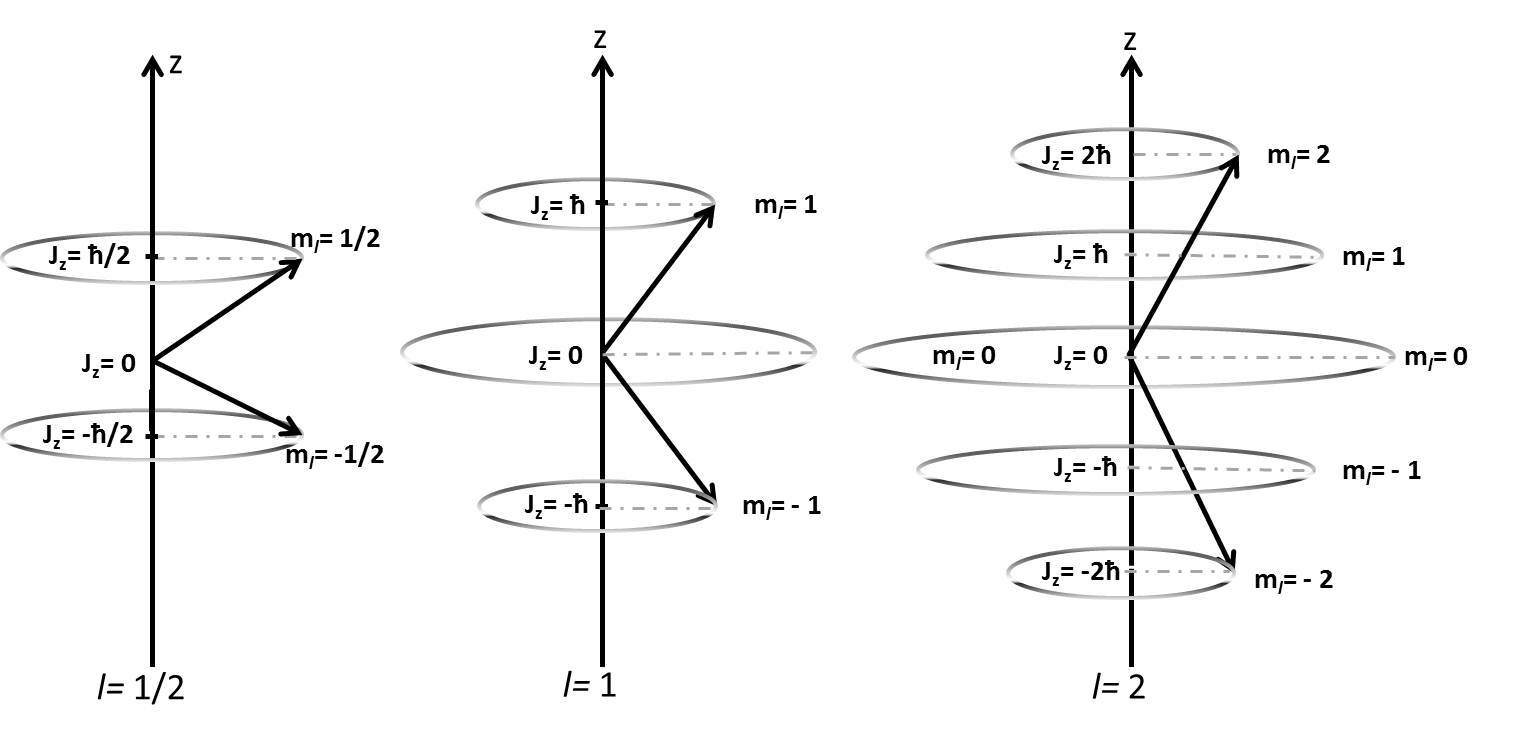
The quantum numbers of the nucleus are denoted below.
| Interaction | Symbol | Quantum Numbers |
|---|---|---|
| Nuclear Spin Angular Momentum | I | 0<I<9/2 by 1/2 |
| Spin Angular Momentum Magnitude | L | \[L=\hbar \sqrt{I(I+1)}\] |
| Spin Angular Momentum Direction | m | \[m=-I, -I+1, -I+2,...+I\] |
Magnetic Moment of a Nucleus
We have now established that the nucleus has spin which can be denoted using specific quantum numbers. As with all charged particles, if the nucleus is moved in a loop it will generate a magnetic field. The magnetic moment \(\mu\) is related to the angular momentum of the nucleus by
\[\mu=\gamma I\]
where \(\gamma\) is the gyromagnetic ratio, a proportionality constant unique to each nucleus. The table below shows some of the gyromagnetic ratios for some commonly studies nuclei.
|
Nuclei |
Unpaired Protons |
Unpaired Neutrons |
Net Spin |
|---|---|---|---|
|
1H |
1 |
0 |
1/2 |
|
2H |
1 |
1 |
1 |
|
31P |
1 |
0 |
1/2 |
|
23Na |
1 |
2 |
3/2 |
|
14N |
1 |
1 |
1 |
|
13C |
0 |
1 |
1/2 |
|
19F |
1 |
0 |
1/2 |
The net or bulk magnetization of the sample is given by \(M\) and is the sum of each individual magnetic vector, or
\[M=\sum{\mu}\]
since these magnetic moments are vectors and are randomly aligned, the bulk magnetization arising from the nucleus is zero. There may be unpaired electrons which give rise to paramagnetic, anti ferromagnetic, or ferromagnetic properties. However, if an external magnetic field is applied, the nuclei will align either with or against the field and result in a non-zero bulk magnetization.
Nuclear Energy Levels in a Magnetic Field
We now understand why the nucleus has a magnetic moment associated with it. Now we are getting to the crux of NMR, the use of an external magnetic field. Initially, the nucleus is in the nuclear ground state which is degenerate. The degeneracy of the ground state is \(2I+1\). The application of a magnetic field splits the degenerate 2I+1 nuclear energy levels. The energy of a particular level is
\[E=-\mu\cdot B_0\]
where \(B_0\) is the external magnetic field. Along the z-direction, which we assume the magnetic field is applied,
\[E=-\mu B_0\]
by substitution,
\[E=-m\hbar\gamma B_0\]
The magnitude of the splitting therefore depends on the size of the magnetic field. In most labs this magnetic field is somewhere between 1 and 21T. Those spins which align with the magnetic field are lower in energy, while those that align against the field are higher in energy.
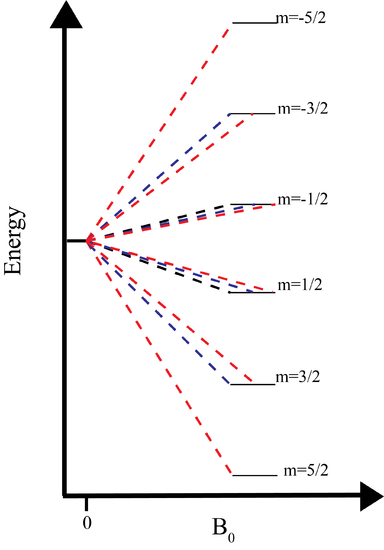
Energy Level Spin Distribution
In the absence of a magnetic field the magnetic dipoles are oriented randomly and there is no net magnetization (vector sum of µ is zero). Application of an external magnetic field, as was shown above, creates distinct energy levels based on the spin angular momentum of the nucleus. Each energy level is populated by the spins which have the same angular momentum. To illustrate this, consider a I=1/2 system. There are two energy levels, +1/2 and -1/2, which are populated by spins that have aligned against or with the external magnetic field, respectively.
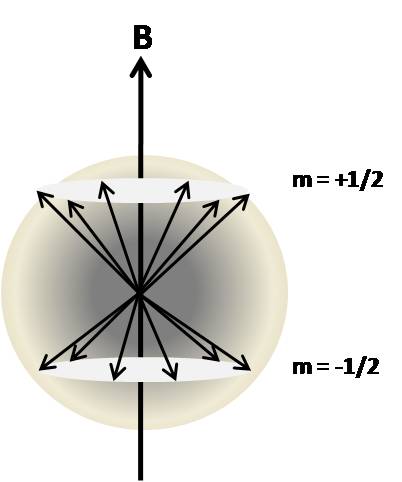
The energy separation between these states is relatively small and the energy from thermal collisions is sufficient to place many nuclei into higher energy spin states. The number of nuclei in each spin state can be described by the Boltzmann distribution. The Boltzmann equation expresses the relationship between temperature and the related energy as shown below.
\[ \large \frac{N_{upper}}{N_{lower}}=e^{\frac{-\Delta{E}}{kT}} = e^{\frac{-h\nu}{kT}} \]
Where Nupper and Nlower represent the population of nuclei in upper and lower energy states, E is the energy difference between the spin states, k is the Boltzmann constant (1.3805x10-23 J/Kelvin ) and T is the temperature in K. At room temperature, the number of spins in the lower energy level, N lower, slightly outnumbers the number in the upper level, N upper.
Selection Rules
The selection rule in NMR is
\[\Delta m=\pm1\]
For a nucleus with I=1/2 there is only one allowed transition. For nuclei with \(I>1/2\), there are multiple transitions which can take place. Consider the case of I=3/2. The following transitions can take place
\[-\dfrac{3}{2}\leftrightarrow-\frac{1}{2}\]
\[-\dfrac{1}{2}\leftrightarrow\frac{1}{2}\]
\[\dfrac{1}{2}\leftrightarrow\frac{3}{2}\]
which is illustrated below.

The transition from
\[-\frac{3}{2}\leftrightarrow-\frac{1}{2}\]
\[\frac{1}{2}\leftrightarrow\frac{3}{2}\]
are known as satellite transitions, while the
\[-\frac{1}{2}\leftrightarrow\frac{1}{2}\]
transition is known as the central transition. The central transition is primarily observed in an NMR experiment. For more information about satellite transitions please look at quarupole interactions.
The NMR Experiment
During the NMR experiment several things happen to the nucleus, the bulk magnetization is rotated from the z axis into the xy plane and then allowed to relax back along the z-axis. A full theoretical explanation for a single atom was developed by Bloch into a set of equations known as the Bloch equations. From the NMR experiment chosen a variety of information can be gleaned by studying different interactions.
References
- Claude H. Yoder, Charles D. Schaeffer,Introduction to multinuclear NMR : theory and application, Benjamin/Cummings Pub. Co., Menlo Park, Calif., 1987.
- Robin K. Harris, Nuclear magnetic resonance spectroscopy : a physicochemical view, Pitman, Marshfield, Mass., 1983.
- Jeremy K.M. Sanders and Brian K. Hunter, Modern NMR spectroscopy : a guide for chemists, Oxford University Press, New York, 1993.
- David A.R. Williams ; editor, David J. Mowthorpe, Nuclear magnetic resonance spectroscopy, Published on behalf of ACOL, London, by J. Wiley, New York, 1986.
- Frank A. Bovey, Lynn Jelinski, Peter A. Mirau, Nuclear magnetic resonance spectroscopy, Academic Press, San Diego, 1988.
- R.J. Abraham, J. Fisher and P. Loftus, Introduction to NMR spectroscopy, Wiley, New York, 1988.
- J.W. Akitt, NMR and chemistry : an introduction to modern NMR spectroscopy, Chapman & Hall, London; New York, 1992.
Contributors
- Derrick Kaseman (UC Davis), Sureyya OZCAN, Siyi Du

