NMR - Background Physics and Mathematics
- Page ID
- 1798
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Page Under Construction!
Introduction
This section will be devoted to understanding basic math and physics that are commonly encountered in NMR theory. These explanations are going to be very simple and concise and the reader is encouraged to look at the references and other wiki pages for fuller discussions.
Spin Angular Momentum
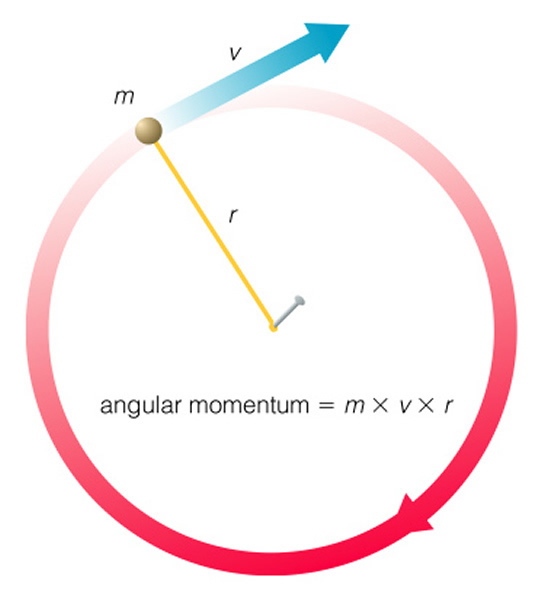
When talking about the spin angular momentum, nucleus can be considered as a mass point moving on a circular path. While the momentum of a mass point moving along the straight path can be defined as
\[ \vec{p}=m\vec{v}\]
(where p and v are vectors), angular velocity is used to describe the motion of nucleus.
\[ \vec{L}=\vec{r} \times \vec{p}\]
(where L is angular momentum and r is the radius of the circle path)
Since L and p are perpendicular to each other, so
\[ L=rp \sin\,90^o=rp\]
\[{p}=m{v}\]
\[L=rmv\]
The direction of L is determined by right-hand rule, so it is perpendicular to the circle plane.
Spherical Coordinates
For more advanced concepts in NMR, a spherical basis set is easier to use. Lets first consider a vector in Cartesian space which can be described by
\[A=A_xe_x+A_ye_yA_ze_z\]
where Ax,y,z is the projection of A onto the x y and z axes, and ex,y,z are the basis vectors.
The length of the vector is
\[|A|=\sqrt{A_x^2+A_y^2+A_z^2}\]
Now switching to a spherical basis set A becomes
\[A=A^{+1}e_{+1}+A^{0}e_{0}+A^{-1}e_{-1}=A_{+1}e+{+1}+A_{0}e+{0}+A_{-1}e+{-1}\]
where the relation of the spherical basis set to the Cartesian basis set is
\[e_{\pm 1}=-e^{\mp 1}=\mp\frac{1}{\sqrt{2}}(e_x \pm ie_y)\]
\[e_0=e^0=e_z\]
\[A_{\pm 1}=-A^{\mp 1}=\mp \frac{1}{\sqrt{2}}(A_x \pm iA_y)\]
\[A_0=A^0=A_z\]
Typically, Ap and Ap are called the contravariant and covariant components, while ep and ep are the contravariant and covariant basis vectors, respectively.
Diagonalization of a Matrix
Euler Angles
Euler Angles are a set of 3 angles that transform reference frames. These are commonly employed in NMR to switch between reference frames. For example one set of Euler angles takes you from the laboratory frame to the rotating frame. A second set of Euler angle can take you from the laboratory from the the CSA tensor frame. Below I've shown the ranges and how the rotations work. More information may be found in Rotations section.
insert figure
\(\gamma\) and \(\alpha\) range the full 2\(\pi\) radians while \(\beta\) ranges \(\pi\) radians
Unitary Evolution
According the 4th postulate of quantum mechanics "The evolution of a closed system is unitary (reversible). The evolution given by the time-dependent Schrödinger equation
\[i\ bar{h} \frac{d| \psi>}{dt}=H| \psi >\]
where H is the Hamiltonian of the system and \(\bar{h}\) is the reduced Planck constant."
We can then express the evolution of a state using a unitary operator, known as the propagator
\[\psi(x,t)=\hat{U}(t) \psi (x,0)\]
where the adjoint of the propagator is equal to the unity operator. We can show that this is equivalent to the time dependent shcrodinger equation.
\[i \bar{h} \frac{\hat{U} \psi(x,0)}{dt}=H \hat{U} \psi (x,0)\]
Since this equation must hold for any wave function then it also msut hold for \(\psi(x,0)\) as well giving
\[i \bar{h}\frac{d \hat{U}}{dt}=H \hat{U}\]
The only way this equation is solved is if the Hamiltonian is time independent and
\[\hat{U}(t)=e^{\frac{-iHt}{\bar{h}}}\]
Fourier Transform
Mathmatical formula that takes you between frequency space and time space
Cross Product of 2 Matricies
Consider 2 2x2 matricies of the form
\[A=\begin{bmatrix} a_{11}&a_{12}\\a_{21}&a_{22} \end{bmatrix}\]
\[B=\begin{bmatrix} b_{11}&b_{12}\\b_{21}&b_{22} \end{bmatrix}\]
the cross product is then defines as
\[A \times B=\begin{bmatrix} a_{11}b_{11} & a_{11}b_{12} & a_{12}b_{11}& a_{12}b_{12}\\ a_{11}b_{21} & a_{11}b_{22} & a_{12}b_{21}& a_{12}b_{22}\\a_{21}b_{11} & a_{21}b_{12} & a_{22}b_{11}& a_{22}b_{12}\\a_{21}b_{21} & a_{21}b_{22} & a_{22}b_{21}& a_{22}b_{22}\end{bmatrix}\]