NMR: Kinetics
- Page ID
- 1830
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Nuclear magnetic resonance (NMR) is an analytical technique used in chemistry to help identify chemical compounds, obtain information on the geometry and orientation of molecules, as well as to study chemical equilibrium of species undergoing physical changes of composition, among many others. Capitalizing on the ability to manipulate the magnetization through different pulse programs in NMR, allows for the study and understanding of the kinetics of a system. The exchange rates between two sites can be evaluated through dynamic nuclear magnetic resonance experiments (DNMR). 17O is a common, NMR active nucleus that is used in the study of kinetics.
Introduction
NMR uses radio frequency radiation to change the direction of nuclear spins that have been placed in a static magnetic field, and measures the change of magnetization as a function of time. Since its discovery, NMR has gone through many advancements that have enabled it to become a very useful analytical technique. The Fourier Transform NMR has enabled more complicated studies through the ability to create pulse programs that can manipulate the spectra, like saturate one species magnetization so no peak is produced. These pulse programs can also be used to tip the spin of certain nuclei, while keeping others along the z-axis. This is useful for many applications, including being able to quench signals, change the direction (positive or negative) of the signal, and track relaxation, to name a few examples. Using different pulse programs allows for the study of exchange rates between species. This is done by monitoring the changes in the environment of the NMR active nuclei as a result exchange between the sites. Because of the exchange, spins (magnetization) will be transferred, leading to changes in the bulk magnetization at both sites. Any NMR active nuclei can be used to study exchange rates, such as 13C, 1H, 17O, but 17O kinetic studies are often performed. This is done because 17O enriched water can be used as one of the exchange sites, normally the bulk solvent site.
17O NMR for Kinetics Studies
Background and Equations
Oxygen seventeen nuclei have a spin state of 5/2, making them susceptible to nuclear magnetic resonance. This isotope of oxygen is only 0.0373% naturally abundant, but using isotopically labeled oxygen compounds can result in useful information. Studying these nuclei in the presence of a magnetic field will provide information about the structure and environment of the oxygens in the molecule. Using dynamic NMR or DNMR, 17O NMR experiments can be performed to understand chemical reactivity and kinetics of compounds. DNMR studies the effect of a chemical exchange between two sites that have either a different chemical shift or coupling constant. These studies are done by obtaining NMR spectra over time and analyzing the increase and/or decrease of the signals. Unlike other methods that are used to study kinetics, NMR studies can acquire information about the effects of the exchange on the molecules.
To utilize NMR spectra to establish kinetic information, the Bloch equations must be adapted to include terms that take into account relaxation as a result of chemical reactivity. While investigating exchange reaction of 17O water between two sites, the bulk water and water bound to a metal, it is assumed that the kinetics are 1st order, such that:
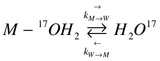
\[\dfrac{du_M}{dt}=-\overrightarrow{k}_M u_M +\overleftarrow{k} _W u_W\]
\[\dfrac{du_W}{dt}=-\overleftarrow{k}_W u_W + \overrightarrow{k}_M u_M\]
Where \(\vec{k}_M\) & \(\vec{k}_W\) represent the rate of exchange between the bulk water and the bound water. These two sites can be said to be coupled because the isotopically enriched oxygen is exchanging between the metal site and bulk water site. As exchange occurs, the magnetization of the 17O metal ensemble and 17O water ensemble will change, not only due to magnetization relaxation, but also due to the exchange. The exchange rate terms can be added into the Bloch equations to take into account the relaxation. With the addition of this term, the equations are known as the Bloch-McConnell equations. Since there are two sites and three Bloch equations per site, there is a total of six equations for the change in magnetization of the system. Equations 1-3 are for the metal site, while Equations 4-6 are for the bulk water site.
Bloch-McConnell Equations for Metal Site (Equations 1-3)
\[\dfrac{du_M}{dt} = v_M(\omega_{rf} - \omega_o)-\dfrac{u_M}{T_{2M}} -\overrightarrow{k}_M u_M + \overleftarrow{k}_W u_W\]
\[\dfrac{dv_M}{dt} = -u_M(\omega_{rf} - \omega_o)-\dfrac{v_M}{T_{2M}} - \overrightarrow{k}_M v_M + \overleftarrow{k}_W v_W\]
\[\dfrac{dm_{zM}}{dt} = v_M \omega_1-\dfrac{(m_{zM}-m_o)}{T_{1M}} - \overrightarrow{k}_M m_{zM} + \overleftarrow{k}_W m_{zW}\]
Bloch-McConnell Equations for Bulk Water Site (Equations 4-6)
\[dfrac{du_W}{dt} = v_W(\omega_{rf} - \omega_o)-\dfrac{u_W}{T_{2W}} - \overleftarrow{k}_W u_W + \overrightarrow{k}_M u_M\]
\[dfrac{dv_W}{dt} = -u_W(\omega_{rf} - \omega_o)-\dfrac{v_W}{T_{2W}} - \overleftarrow{k}_W v_W + \overrightarrow{k}_M v_M\]
\[dfrac{dm_{zW}}{dt} = v_W \omega_1-\dfrac{(m_{zM}-m_o)}{T_{1W}} - \overleftarrow{k}_W m_{zW} + \overrightarrow{k}_M m_{zM}\]
To analyze the NMR spectra, which is obtained by measuring the magnetization in the x-y plane, requires an equation that explains the magnetization change in the x-y plane as a function of time. In the rotating frame, the total magnetization in the x-y plane is comprised of two components the “real” and “imaginary” parts. Therefore, the total magnetization in the x-y plane can be expressed \(m_{xy}=u+iv\), or \(u=m_{xt}-iv\). Taking the derivative of this equation with respect to time leads to \(\frac{dm_{xy}}{dt}=\frac{du}{dt}+i\frac{dv}{dt}\). Using the previous relationships, the Bloch equations for the two sites can be simplified and rearranged to give the magnetization in the x-y place as a function of time. Invoking the law of detailed balance, which states that the exchange rate of the metal site times the amount of 17O at this site is equal to the exchange rate of the bulk water site times the amount of 17O at this site, will eliminate one of the rate coefficients, simplifying the equations even further gives Equation 7.
Equation 7:

