Solomon Equations
- Page ID
- 61683
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
The Solomon equations describe the relaxation between two coupled spins, I and S. This page will be dedicated to developing a theoretical treatment beginning from the Bloch equations. We will investigate the ramifications of the relaxation and the consequences on the overall relaxation rates.
Theoretical Treatment
We begin by describing a system of two spins, I and S. Each spin has two states; low energy \(\alpha\) and high energy \(\beta\) and we can then come up with a 4 level energy system for these two spins. This is shown in the figure below.

A spin can have allowed relaxation induced transitions between the \(\alpha\) and \(\beta\) states which occur at a rate (W1IS) as well as forbidden relaxation induced transitions between like states (W2), which are shown in the figure below. Forbidden transitions W2 corresponds to both spins flipping, known as a flip-flip transition, while W0 is where each spin flips between states, known as a flip-flop transition. The superscripts denote the order (zero, single, double) type of transition.
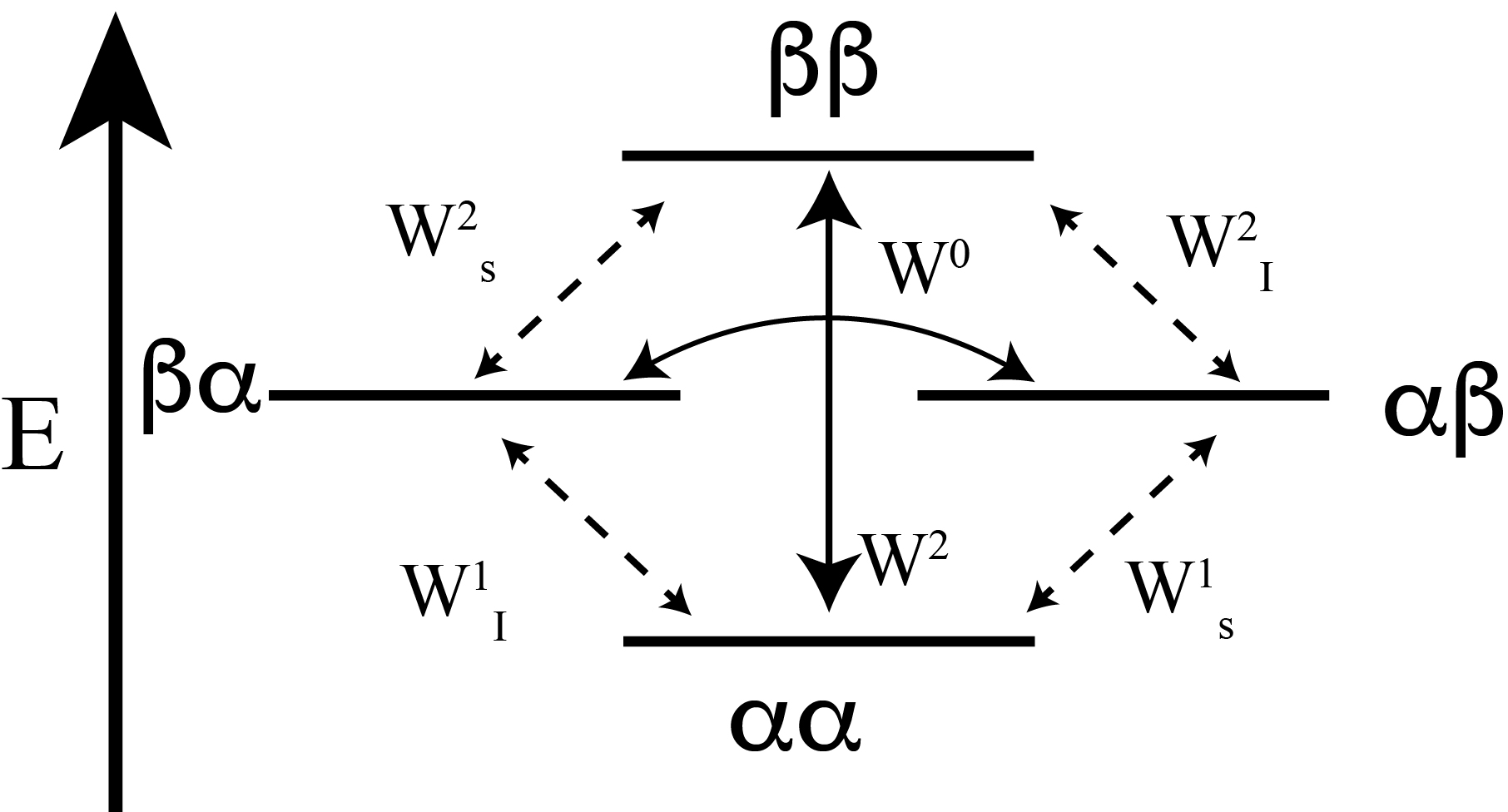
We can now define the change in the population of each level in with 1=\(\alpha \alpha\) 2=\(\beta \alpha\), 3= \(\alpha \beta\) and 4=\(\beta \beta\) during a given amount of time. For example, for energy level 1, the population is initially n10. As time progress, the some of this population will go to energy levels 2, 3, and 4 at rates, W1I, W1S, W2, respectively. Meanwhile the state will gain population from states 2, 3, and 4 at at rates, W1I, W1S, W2, respectively. It may seem that this would give a net result of 0, but the populations of each state is given by the Boltzmann distribution and the argument may be easily made that the rate will depend on the number of spins in the given energy level. Therefore we may now write:
\[\dfrac{dn_1}{dt}=-W_S^1n_1-W_I^1n_1-W^2n_1+W_S^1n_3+W_I^1n_2+W^2n_4\] (eq. 1)
the rates for the other energy levels may then be written as:
\[\dfrac{dn_2}{dt}=+W_I^1n_1+W_S^2n_4+W^0n_3-W_S^2n_2-W_I^1n_2-W^0n_2\] (eq. 2)
\[\dfrac{dn_3}{dt}=+W_S^1n_1+W_I^2n_4+W^0n_2-W_I^2n_3-W_S^1n_3-W^0n_3\](eq. 3)
\[\dfrac{dn_4}{dt}=-W_S^2n_4-W_I^2n_4-W^2n_4+W_I^2n_3+W_S^2n_2+W^2n_1\](eq. 4)
We can then calculate the spin magnetization for the I and S spins, along the Z axis. The reason for the Z axis is because we are concerned with the recovery of the magnetization to it's equilibrium value. Therefore, the net magnetization for spin I will be the difference in populations between the I transitions and is expressed as
\[I_z=n_1-n_2+n_3-n_4\] (eq. 5)
and spin S will be
\[S_z=n_1-n_3+n_2-n_4.\] (eq. 6)
Further we can define the difference in populations between the 2 I-spin transitions, n1-n2-n3+n4, which is the same for the 2 S-spin transitions and will be denoted 2IzSz.
\[2I_zS_z=n_1-n_2-n_3+n_4.\] (eq. 7)
The total population of the system is then given by
\(T=n_1+n_2+n_3+n_4\) (eq. 8)
And ni can then be re-written as a combination of Iz, Sz, 2IzSz, and T such that
\(n_1=\dfrac{1}{4}(T+I_z+S_z+2I_zS_z)\) (eq. 9)
\(n_2=\dfrac{1}{4}(T-I_z+S_z-2I_zS_z)\) (eq. 10)
\(n_3=\dfrac{1}{4}(T+I_z-S_z-2I_zS_z)\) (eq. 11)
\(n_4=\dfrac{1}{4}(T-I_z-S_z+2I_zS_z)\) (eq. 12)
Which can be verified by plugging equations 5-8 into equations 9-12.
Derivation of The Solomon Equations
The Solomon equations are the time-dependent operators Iz, Sz, and 2IzSz expressed in terms of W and the operators. We will take the following approach to derive each operator:
1) Take the time derivative of each operator.
2) Express the derivative in terms of W by substituting equations 1-4 for \(\dfrac{dn_i}{dt}\).
3) Group the ni terms.
4) Substitute the equations 9-12 for ni and group the like W terms. This will give the final equations.
Each step will be numbered according to this list.
Derivation of Iz
1) \(\dfrac{dI_z}{dt}=\dfrac{dn_1}{dt}-\dfrac{dn_2}{dt}+\dfrac{dn_3}{dt}-\dfrac{dn_4}{dt}\)
2) \(=-W_S^1n_1-W_I^1n_1-W^2n_1+W_S^1n_3+W_I^1n_2+W^2n_4\)
\(-(+W_I^1n_1+W_S^2n_4+W^0n_3-W_S^2n_2-W_I^1n_2-W^0n_2)\)
\(+(+W_S^1n_1+W_I^2n_4+W^0n_2-W_I^2n_3-W_S^1n_3-W^0n_3)\)
\(-(-W_S^2n_4-W_I^2n_4-W^2n_4+W_I^2n_3+W_S^2n_2+W^2n_1)\)
3) \(\dfrac{dI_z}{dt}=-2n_1[W_I^1+W^2]+2n_2[W_I^1+W^0]-2n_3[W_I^2+W^0]+2n_4[W_I^2+W^2]\)
4) \(W^2[-2\dfrac{1}{4}*(T+I_z+S_z+2I_zS_z)+2\frac{1}{4}(T-I_z-S_z+2I_zS_z)]=W^2(-I_z-S_z)\)
\(W_I^1[-2\dfrac{1}{4}(T+I_z+S_z+2I_zS_z)+2\dfrac{1}{4}(T-I_z+S_z-2I_zS_z)=W_1^1(-I_z-2I_zS_z)\)
\(W^0[2\dfrac{1}{4}(T-I_z+S_z-2I_zS_z)+-2\dfrac{1}{4}(T+I_z-S_z-2I_zS_z)]=W^0(-I_z+S_z)\)
\(W_I^2[-2\dfrac{1}{4}(T+I_z-S_z-2I_zS_z)+2\dfrac{1}{4}(T-I_z-S_z+2I_zS_z)]=W_I^2(-I_z+2I_zS_z)\)
\(\dfrac{dI_z}{dt}=-(W_I^1+W_I^2+W^2+W^0)I_z-(W^2-W^0)S_z-(W_I^1-W_I^2)2I_zS_z\)
Derivation of Sz
\[S_z=n_1-n_3+n_2-n_4.\]
1) \(\dfrac{dS_z}{dt}=\dfrac{n_1}{dt}-\dfrac{n_3}{dt}+\dfrac{n_2}{dt}-\dfrac{n_4}{dt}\)
2) \(\dfrac{dS_z}{dt}=[-W_S^1n_1-W_I^1n_1-W^2n_1+W_S^1n_3+W_I^1n_2+W^2n_4]\)
\(-[+W_S^1n_1+W_I^2n_4+W^0n_2-W_I^2n_3-W_S^1n_3-W^0n_3]\)
\(+[W_I^1n_1+W_S^2n_4+W^0n_3-W_S^2n_2-W_I^1n_2-W^0n_2]\)
\(-[-W_S^2n_4-W_I^2n_4-W^2n_4+W_I^2n_3+W_S^2n_2+W^2n_1]\)
3) \(\dfrac{dS_z}{dt}=\)\(-2n_1[W_S^1+W^2]\)\(-2n_2[W^0+W_S^2]\)\(+2n_3[W_S^1+W^0]\)\(+2n_4[W^2+W_S^2]\)
4) \(2\dfrac{1}{4}W_S^1[(-T-I_z-S_z-2S_zI_z)+(T+I_z-S_z-2I_zS_z)]=W_S^1(-S_z-2I_zS_z)\)
\(2\dfrac{1}{4}W^2[(-T-I_z-S_z-2S_zI_z)+(T-I_z-S_z+2I_zS_z)]=W^2(I_z+S_z)\)
\(2\dfrac{1}{4}W^0[(-T+I_z-S_z+2S_zI_z)+(T+I_z-S_z-2I_zS_z)]=W^0(I_z-S_z)\)
\(2\dfrac{1}{4}W_S^21[(-T-I_z+S_z+2S_zI_z)+(T-I_z-S_z+2I_zS_z)]=W_S^2(-S_z-2I_zS_z)\)
\(\dfrac{dS_z}{dt}=-S_z(W_S^1+W^2+W^0+W_S^2)+2I_zS_z(W_S^2-W_S^1)+I_z(W^0-W^2)\)
Deriving 2IzSz
\[2I_zS_z=n_1-n_2-n_3+n_4.\]
1)\(\dfrac{d2I_zS_z}{dt}=\dfrac{n_1}{dt}-\dfrac{n_2}{dt}-\dfrac{n_3}{dt}+\dfrac{n_4}{dt}\)
2)\(\dfrac{d2I_zS_z}{dt}=[-W_S^1n_1-W_I^1n_1-W^2n_1+W_S^1n_3+W_I^1n_2+W^2n_4]\)
\(-[W_I^1n_1+W_S^2n_4+W^0n_3-W_S^2n_2-W_I^1n_2-W^0n_2]\)
\(-[W_S^1n_1+W_I^2n_4+W^0n_2-W_I^2n_3-W_S^1n_3-W^0n_3]\)
\(+[-W_S^2n_4-W_I^2n_4-W^2n_4+W_I^2n_3+W_S^2n_2+W^2n_1]\)
3)\(\dfrac{d2I_zS_z}{dt}=-2n_1(W_S^1+W_I^1)+2n_2(W_I^1+W_S^2)+2n_3(W_S^1+W_I^2)-2n_4(W_S^2+W_I^2)\).
4)\(W_S^1[-2\dfrac{1}{4}(T+I_z+S_z+2I_zS_z)+2\dfrac{1}{4}(T+I_z-S_z-2I_zS_z)]=-W_S^1[S_z+2I_zS_z]\)
\(W_I^1[-2\dfrac{1}{4}(T+I_z+S_z+2I_zS_z)+2\dfrac{1}{4}(T-I_z+S_z-2I_zS_z)]=W_I^1[I_z+2I_zS_z]\)
\(W_S^2[-2\dfrac{1}{4}(T-I_z+S_z-2I_zS_z)-2\dfrac{1}{4}(T-I_z-S_z+2I_zS_z)]=-W_S^2[S_z-2I_zS_z]\)
\(W_I^2[-2\dfrac{1}{4}(T+I_z-S_z-2I_zS_z)-2\dfrac{1}{4}(T-I_z-S_z+2I_zS_z)]=W_I^2[I_z-2I_zS_z]\)
\(\dfrac{d2I_zS_z}{dt}=S_z(W_S^2-W_S^1)+I_z(W_I^2-W_I^1)-2I_zS_z(W_S^2+W_S^1+W_I^2+W_I^1)\)
Relaxation Mechanisms of the Solomon equations
The Solomon equations for operators Iz, Sz, and 2IzSz are given below (in case the reader skips the derivation)
\(\dfrac{I_z}{dt}=-(W_I^1+W_I^2+W^2+W^0)I_z-(W^2-W^0)S_z-(W_I^1-W_I^2)2I_zS_z\)
\(\dfrac{S_z}{dt}=-S_z(W_S^1+W^2+W^0+W_S^2)+2I_zS_z(W_S^2-W_S^1)+I_z(W^0-W^2)\)
\(\dfrac{2I_zS_z}{dt}=S_z(W_S^2-W_S^1)+I_z(W_I^2-W_I^1)-2I_zS_z(W_S^2+W_S^1+W_I^2+W_I^1)\)
Now, these equations are not quite right, as the treatment that we gave actually considers only the perturbed spins. Therefore we may now re-write these equations to account for the the spins that are perturbed by defining the perturbed spins as the perturbed population+equilibrium population=Iz, while the equilibrium population is I0z. The equations may now be re-written as
\(\dfrac{I_z-I_z^0}{dt}=-(W_I^1+W_I^2+W^2+W^0)(I_z-I_z^0)-(W^2-W^0)(S_z-S_z^0)-(W_I^1-W_I^2)\)
\(\dfrac{S_z-S_z^0}{dt}=-(S_z-S_z^0)(W_S^1+W^2+W^0+W_S^2)+2I_zS_z(W_S^2-W_S^1)+(I_z-I_z^0)(W^0-W^2)\)
\(\dfrac{2I_zS_z}{dt}=(S_z-S_z^0)(W_S^2-W_S^1)+(I_z-I_z^0)(W_I^2-W_I^1)2I_zS_z(W_S^2+W_S^1+W_I^2+W_I^1)\)
Self Relaxation
The Solomon equations for a given spin, here described for Iz but applicable for Sz and 2IzSz, show that the rate of relaxation is tied to Iz, Sz, and 2IzSz. The rate constants associated with Iz corresponds to the self relaxation of the spin magnetization on its own. This is given by the overall rate
\(W_I^1+W_I^2+W^2+W^0\)
Note that the rates W2 and W0 correspond to processes cross-relaxation processes that need a spin S to occur. Therefore, the relaxation rate for Iz is not dependent on any other spins in the system. The summation of the rate constants is denoted by RI.
Cross-Relaxation
The term (W0-W2)Sz is present in the Solomon equations for Iz and corresponds to the the rate at which Sz transfers magnetization to Iz spin magnetization in a phenomenon is known as cross-relaxation. To properly illustrate the effect, take \(W^2=W^0=0\). In this case, relaxation of a spin I is independent of spin S. On the other hand, if \(W^2 and/or W^0\neq0\) but spin S is not perturbed, (i.e, (\(S_z-S_z^0)=0\)) cross relaxation will not occur either. The cross relaxation term is denoted as \(\sigma_{IS}\).
2IzSz Relaxation
The relaxation associated with \(W_I^1-W_I^2\) is the transfer of magnetization from IzSz to I, denoted as \(\Delta_{I}\), which will only occur if the rate constants are different. Meanwhile the operatore 2IzSz also shows self-relaxation as RIS, denoted by
\(R_{IS}=W_I^1+W_I^2+W_S^1+W_S^2\)
References
1) I.Solomon. "Relaxation Processing in a System of Two Spins" Phys. Rev. 99, 1955, 559.
2) J. Keeler. "Relaxation" Chapter 8 2004
3) M. Levitt. "Spin Dyanmics"

