Electron Spin
- Page ID
- 1651
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Electron Spin or Spin Quantum Number is the fourth quantum number for electrons in atoms and molecules. Denoted as \(m_s\), the electron spin is constituted by either upward (\(m_s=+1/2\)) or downward (\(m_s=-1/2\)) arrows.
Introduction
In 1920, Otto Stern and Walter Gerlach designed an experiment, which unintentionally led to the discovery that electrons have their own individual, continuous spin even as they move along their orbital of an atom. Today, this electron spin is indicated by the fourth quantum number, also known as the Electron Spin Quantum Number and denoted by ms. In 1925, Samuel Goudsmit and George Uhlenbeck made the claim that features of the hydrogen spectrum that were unexamined might by explained by assuming electrons act as if it has a spin. This spin can be denoted by an arrow pointing up, which is +1/2, or an arrow pointing down, which is -1/2.
The experiment mentioned above by Otto Stern and Walter Gerlach was done with silver which was put in an oven and vaporized. The result was that silver atoms formed a beam that passed through a magnetic field in which it split in two.
An explanation of this is that an electron has a magnetic field due to its spin. When electrons that have opposite spins are put together, there is no net magnetic field because the positive and negative spins cancel each other out. The silver atom used in the experiment has a total of 47 electrons, 23 of one spin type, and 24 of the opposite. Because electrons of the same spin cancel each other out, the one unpaired electron in the atom will determine the spin. There is a high likelihood for either spin due to the large number of electrons, so when it went through the magnetic field it split into two beams.
Brief Explanation of Quantum Numbers
Note: In this module, capital "L" will be used instead of small case "l" for angular momentum quantum number.
A total of four quantum numbers were developed to better understand the movement and pathway of electrons in its designated orbital within an atom.
- Principal quantum number (n): energy level n = 1, 2, 3, 4, ...
- Orbital Angular Momentum Quantum Number (L): shape (of orbital) L = 0, 1, 2, 3, ...n-1
- Magnetic Quantum Number (mL): orientation mL = interval of (-L, +L)
- Electron Spin Quantum Number (ms): independent of other three quantum numbers because ms is always = –½ or +½
(For more information about the three quantum numbers above, see Quantum Number.)

The lines represent how many orientations each orbital has, (e.g. the s-orbital has one orientation, a p-orbital has three orientations, etc.) and each line can hold up to two electrons, represented by up and down arrows. An electron with an up arrow means it has an electron spin of +\(\frac{1}{2}\), and an electron with a down arrow means it has an electron spin of -\(\frac{1}{2}\).
Electron Spin
Significance: determines if an atom will or will not generate a magnetic field (For more information, scroll down to Magnetic Spin, Magnetism, and Magnetic Field Lines). Although the electron spin is limited to +½ or –½, certain rules apply when assigning electrons of different spins to fill a subshell (orientations of an orbital) . For more information, scroll down to Assigning Spin Direction.
Magnetic Spin, Magnetism, and Magnetic Field Lines
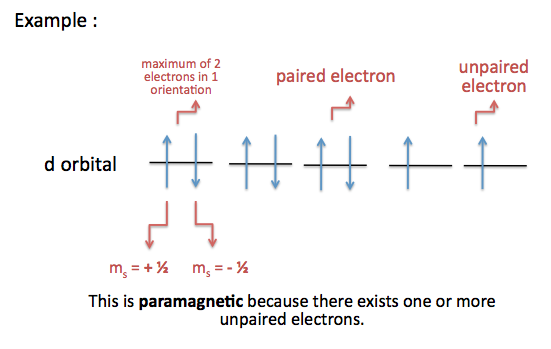
An atom with unpaired electrons are termed as paramagnetic
- results in a net magnetic field because electrons within the orbital are not stabilized or balanced enough
- atoms are attracted to magnets
An atom with paired electrons are termed as diamagnetic
- results in no magnetic field because electrons are uniform and stabilized within the orbital
- atoms are not attracted to magnets
Applying concepts of magnetism with liquid nitrogen and liquid oxygen:
The magnetic spin of an electron follows in the direction of the magnetic field lines as shown below.
.jpg?revision=1)
{{media("www.youtube.com/watch?v=uj0DFDfQajw\)
Assigning Spin Direction
An effective visual on how to assign spin directions can be represented by the orbital diagram (shown previously and below.) Restrictions apply when assigning spin directions to electrons, so the following Pauli Exclusion Principle and Hund's Rule help explain this. The direction of the electron spin magnetic quantum number, ms, can only be determined its interaction with a magnetic field. Electrons whose spin is parallel to an external magnetic field (spin up with +\(\frac{1}{2}\) spin) have a lower energy than those whose magnetic spin is anti-parallel (spin down with -\(\frac{1}{2}\) spin) to the external magnetic and fill first.
When one is filling an orbital, such as the p orbital, you must fill all orbitals possible with spin up electrons before assigning the opposite spin. For example, when filling the fluorine, which will have a total of two electrons in the s orbital and a total of five electrons in the p orbital, one will start with the s orbital which will contain two electrons. So, the first electron one assigns will be spin up and the next spin down. Moving on to the three p orbitals that one will start by assigning a spin up electron in each of the three orbitals. That takes up three of the five electrons, so with the remaining two electrons, one returns to the first and second p orbital and assigns the spin down electron. This means there will be one unpaired electron in fluorine so it will be paramagnetic.
Pauli Exclusion Principle
The Pauli exclusion principle declares that there can only be a maximum of two electrons for every one orientation, and the two electrons must be opposite in spin direction; meaning one electron has \(m_s = +\frac{1}{2}\) and the other electron has \(m_s = -\frac{1}{2}\).
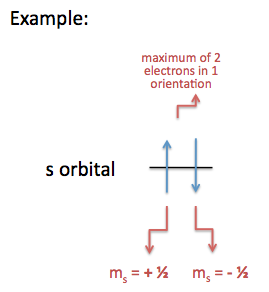
Hund's Rule
Hund's Rule declares that the electrons in the orbital are filled up first by electrons whose spins are parallel to each other. Once all the orbitals are filled with unpaired +\(\frac{1}{2}\) spins, the orbitals are then filled with -\(\frac{1}{2}\) spin. (See examples below, labeled electronic configuration.)
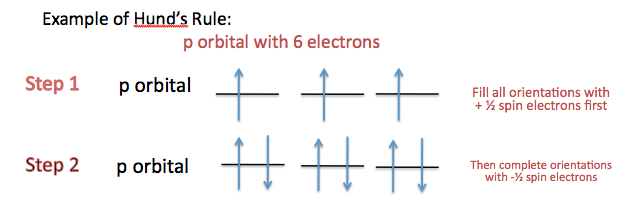
(For more information on Pauli Exclusion Principle and Hund's Rules, see Electronic Configuration.)
Identifying Spin Direction
- Determine the number of electrons the atom has.
- Draw the electron configuration for the atom. See Electronic Configurations for more information.
- Distribute the electrons, using up and down arrows to represent the electron spin direction.
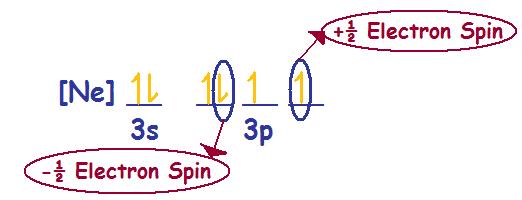
Sulfur - S (16 electrons)
Electronic Configuration:
Principal Quantum Number & (s, p, d, f) Orbitals
When given a principal quantum number, n, with either the s, p, d or f-orbital, identify all the possibilities of L, mL and ms.
Given 5f, identify all the possibilities of the four quantum numbers.
Solution
In this problem, the principal quantum number is n = 5 (the subshell number placed in front of the orbital, the f-orbital in this case). Since we are looking at the f-obital, therefore L = 3. (Look under "Subshells" in the module Quantum Numbers for more information) Knowing L = 3, we can interpret that mL = 0, \(\pm\) 1, \(\pm\) 2, \(\pm\) 3 since mL = -L,...,-1, 0, 1,...+L. As for ms, since it isn't specified in the problem as to whether it is -\(\frac{1}{2}\) or +\(\frac{1}{2}\), therefore for this problem, it could be both; meaning that the electron spin quantum number is \(\pm\)\(\frac{1}{2}\).
Given 6s and mL= +1, identify all the possibilities of the four quantum numbers.
Solution
The principal quantum number is n = 6. Looking at the s-orbital, we know that L = 0. Knowing that mL = -L,...,-1, 0, 1,...+L, therefore mL = +1 is not possible since in this problem, the interval of mL can only equal to 0 according to the angular momentum quantum number, L.
Given 4d and ms = +\(\frac{1}{2}\), identify all the possibilities of the four quantum numbers.
Solution
The principal quantum number is n = 4. Given that it is a d-orbital, we know that L = 2. Therefore, mL = 0, \(\pm\) 1, \(\pm\) 2 since mL = -L,...,-1, 0, 1,...+L. For ms, this problem specifically said ms = +\(\frac{1}{2}\); meaning that the electron spin quantum number is +\(\frac{1}{2}\).
Electron Spin: Where to begin?
First, draw a table labeled n, L, mLand ms, as shown below:
| n | L | mL | ms |
Then, depending on what the question is asking for, fill in the boxes accordingly. Finally, determine the number of electrons for the given quantum number, n, with regards to L, mL and ms.
How many electrons can have n = 5 and L = 1? 6
| n | L | mL | ms |
|
5 |
1 |
-1 | -\(\frac{1}{2}\), +\(\frac{1}{2}\) |
| 0 | -\(\frac{1}{2}\), +\(\frac{1}{2}\) | ||
| +1 | -\(\frac{1}{2}\), +\(\frac{1}{2}\) |
This problem includes both -\(\frac{1}{2}\), +\(\frac{1}{2}\), therefore the answer is 6 electrons based on the three possible values of mL.
How many electrons can have n = 5 and ms = -\(\frac{1}{2}\)? 9
| n | L | mL | ms |
|
5 |
4 | \(\pm\) 4 | -\(\frac{1}{2}\) |
| 3 | \(\pm\) 3 | -\(\frac{1}{2}\) | |
| 2 | \(\pm\) 2 | -\(\frac{1}{2}\) | |
| 1 | \(\pm\) 1 | -\(\frac{1}{2}\) | |
| 0 | 0 | -\(\frac{1}{2}\) |
This problem only wants the Spin Quantum Number to be -\(\frac{1}{2}\), the answer is 9 electrons based on the 9 different values of mL .
How many electrons can have n = 3, L = 2 and mL = 3? zero
Solution
| n | L | mL | ms |
| 3 | 2 | NOT POSSIBLE |
How many electrons can have n = 3, mL = +2 and ms = +\(\frac{1}{2}\)? 1
Solution
| n | L | mL | ms |
|
3 |
2 |
+2 |
+\(\frac{1}{2}\) |
This problem only wants the Spin Quantum Number to be +\(\frac{1}{2}\), the answer is 1 electron based on the value of mL and ms.
References
- Petrucci, Ralph. Harwood, William. Herring, Geoffrey. Madura, Jeffery. General Chemistry: Principles and Modern Applications, 9th Edition. Pearson Education, Inc. New Jersey, 2007.
- Li, Gengyun. What is the Electron Spin? Spin Publishing, 2003.
- Motz, Lloyd and Weaver, Jefferson H. The Unfolding Universe: A Stellar Journey. Perseus, 1989.
Practice Problems
- Identify the spin direction (e.g. ms = -\(\frac{1}{2}\) or +\(\frac{1}{2}\) or \(\pm\)\(\frac{1}{2}\) ) of the outermost electron in a Sodium (Na) atom.
- Identify the spin direction of the outermost electron in a Chlorine (Cl) atom.
- Identify the spin direction of the outermost electron in a Calcium (Ca) atom.
- Given 5p and ms = +\(\frac{1}{2}\), identify all the possibilities of the four quantum numbers.
- Given 6f, identify all the possibilities of the four quantum numbers.
- How many electrons can have n = 4 and L = 1?
- How many electrons can have n = 4, L = 1, mL = -2 and ms = +\(\frac{1}{2}\)?
- How many electrons can have n = 5, L = 3, mL = \(\pm\) 2 and ms = +\(\frac{1}{2}\)?
- How many electrons can have n = 5, L = 4, mL = +3 and ms = -\(\frac{1}{2}\)?
- How many electrons can have n = 4, L = 2, mL = \(\pm\)1 and ms = -\(\frac{1}{2}\)?
- How many electrons can have n = 3, L = 3, mL = +2?
Solutions: Check your work!
Problem (1): Sodium (Na) --> Electronic Configuration [Ne] 3s1

Spin direction for the valence electron or ms = +\(\frac{1}{2}\)
Sodium (Na) with a neutral charge of zero is paramagnetic, meaning that the electronic configuration for Na consists of one or more unpaired electrons.
Problem (2): Chlorine (Cl) --> Electronic Configuration [Ne] 3s2 3p5
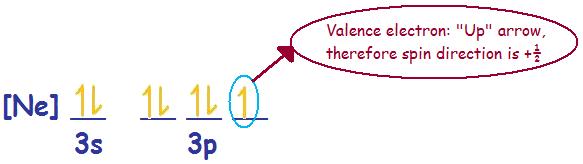
Spin direction for the valence electron or ms = +\(\frac{1}{2}\)
Chlorine (Cl) with a neutral charge of zero is paramagnetic.
Problem (3): Calcium (Ca) --> Electronic Configuration [He] 4s2

Spin direction for the valence electron or ms = \(\pm\)\(\frac{1}{2}\)
Whereas for Calcium (Ca) with a neutral charge of zero, it is diamagnetic; meaning that ALL the electrons are paired as shown in the image above.
Problem (4): Given 5p and ms = -\(\frac{1}{2}\), identify all the possibilities of the four quantum numbers.
The principal quantum number is n = 5. Given that it is a p-orbital, we know that L = 1. And based on L, mL = 0, \(\pm\) 1 since mL = -L,...,-1, 0, 1,...+L. As for ms, this problem specifically says ms = -\(\frac{1}{2}\), meaning that the spin direction is -\(\frac{1}{2}\), pointing downwards ("down" spin).
Problem (5): Given 6f, identify all the possibilities of the four quantum numbers.
The principal quantum number is n = 6. Given that it is a f-orbital, we know that L = 3. Based on L, mL = 0, \(\pm\) 1, \(\pm\) 2, \(\pm\) 3 since mL = -L,...,-1, 0, 1,...+L. As for ms, since it isn't specified in the problem as to whether it is -\(\frac{1}{2}\) or +\(\frac{1}{2}\), therefore for this problem, it could be both; meaning that the electron spin quantum number is \(\pm\)\(\frac{1}{2}\).
Problem (6): How many electrons can have n = 4 and L = 1? 6
| n | L | mL | ms |
| 4 | 1 | \(\pm\) 1 | -\(\frac{1}{2}\), + \(\frac{1}{2}\) |
| 0 |
This problem includes both -\(\frac{1}{2}\), +\(\frac{1}{2}\), therefore the answer is 6 electrons based on the mL.
Problem (7): How many electrons can have n = 4, L = 1, mL = -2 and ms = +\(\frac{1}{2}\)? zero
| n | L | mL | ms |
| 4 | 1 | NOT POSSIBLE | + \(\frac{1}{2}\) |
Since mL = -L...-1, 0, +1...+L, mL is not possible because L = 1, so it is impossible for mL to be equal to 2 when mL MUST be with the interval of -L and +L. So, there is zero electron.
Problem (8): How many electrons can have n = 5, L = 3, mL = \(\pm\) 2 and ms = +\(\frac{1}{2}\)? 2
| n | L | mL | ms |
| 5 | 3 | \(\pm\) 2 | + \(\frac{1}{2}\) |
| \(\pm\) 1 | |||
| 0 |
This problem only wants the Spin Quantum Number to be +\(\frac{1}{2}\) and mL = \(\pm\) 2, therefore 2 electrons can have n = 5, L = 3, mL = \(\pm\) 2 and ms = +\(\frac{1}{2}\).
Problem (9): How many electrons can have n = 5, L = 4 and mL = +3? 2
| n | L | mL | ms |
| 5 | 4 | -3, +3 | -\(\frac{1}{2}\), + \(\frac{1}{2}\) |
| \(\pm\) 2 | |||
| \(\pm\) 1 | |||
| 0 |
This problem includes both -\(\frac{1}{2}\) and +\(\frac{1}{2}\) and given that mL = +3, therefore the answer is 2 electrons.
Problem (10): How many electrons can have n = 4, L = 2 and mL = \(\pm\) 1? 4
| n | L | mL | ms |
| 4 | 2 | \(\pm\) 1 | -\(\frac{1}{2}\), + \(\frac{1}{2}\) |
| 0 |
This problem includes both -\(\frac{1}{2}\) and +\(\frac{1}{2}\) and given that mL = \(\pm\) 1, therefore the answer is 4 electrons.
Problem (11): How many electrons can have n = 3, L = 3, mL = +2 and ms = -\(\frac{1}{2}\)? zero
| n | L | mL | ms |
| 3 | 3 (NOT POSSIBLE) | \(\pm\) 2 | -\(\frac{1}{2}\) |
| \(\pm\) 1 | |||
| 0 |
Since L = n - 1, there is zero electron, not possible because in this problem, n = L = 3.
Contributors and Attributions
- Liza Chu (UCD), Sharon Wei (UCD), Mandy Lam (UCD), Lara Cemo (UCD)

