Electronic Orbitals
- Page ID
- 1650
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)An atom is composed of a nucleus containing neutrons and protons with electrons dispersed throughout the remaining space. Electrons, however, are not simply floating within the atom; instead, they are fixed within electronic orbitals. Electronic orbitals are regions within the atom in which electrons have the highest probability of being found.
Quantum Numbers describing Electronic Orbitals
There are multiple orbitals within an atom. Each has its own specific energy level and properties. Because each orbital is different, they are assigned specific quantum numbers: 1s, 2s, 2p 3s, 3p,4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p. The numbers, (n=1,2,3, etc.) are called principal quantum numbers and can only be positive numbers. The letters (s,p,d,f) represent the orbital angular momentum quantum number (ℓ) and the orbital angular momentum quantum number may be 0 or a positive number, but can never be greater than n-1. Each letter is paired with a specific ℓ value:
An orbital is also described by its magnetic quantum number (mℓ). The magnetic quantum number can range from –ℓ to +ℓ. This number indicates how many orbitals there are and thus how many electrons can reside in each atom.
Orbitals that have the same or identical energy levels are referred to as degenerate. An example is the 2p orbital: 2px has the same energy level as 2py. This concept becomes more important when dealing with molecular orbitals. The Pauli exclusion principle states that no two electrons can have the same exact orbital configuration; in other words, the same quantum numbers. However, the electron can exist in spin up (ms = +1/2) or with spin down (ms = -1/2) configurations. This means that the s orbital can contain up to two electrons, the p orbital can contain up to six electrons, the d orbital can contain up to 10 electrons, and the f orbital can contain up to 14 electrons.
| s subshell | p subshell | d subshell | f subshell |
|---|---|---|---|
| ℓ = 0 | ℓ = 1 | ℓ = 2 | ℓ = 3 |
| mℓ = 0 | mℓ= -1, 0, +1 | mℓ= -2, -1, 0, +1, +2 | mℓ= -3, -2, -1, 0, +1, +2, +3 |
| One s orbital | Three p orbitals | Five d orbitals | Seven f orbitals |
| 2 s orbital electrons | 6 p orbital electrons | 10 d orbital electrons | 14 f orbital electrons |
Visualizing Electron Orbitals
As discussed in the previous section, the magnetic quantum number (ml) can range from –l to +l. The number of possible values is the number of lobes (orbitals) there are in the s, p, d, and f subshells. As shown in Table 1, the s subshell has one lobe, the p subshell has three lobes, the d subshell has five lobes, and the f subshell has seven lobes. Each of these lobes is labeled differently and is named depending on which plane the lobe is resting in. If the lobe lies along the x plane, then it is labeled with an x, as in 2px. If the lobe lies along the xy plane, then it is labeled with a xy such as dxy. Electrons are found within the lobes. The plane (or planes) that the orbitals do not fill are called nodes. These are regions in which there is a 0 probability density of finding electrons. For example, in the dyx orbital, there are nodes on planes xz and yz. This can be seen in Figure \(\PageIndex{1}\).
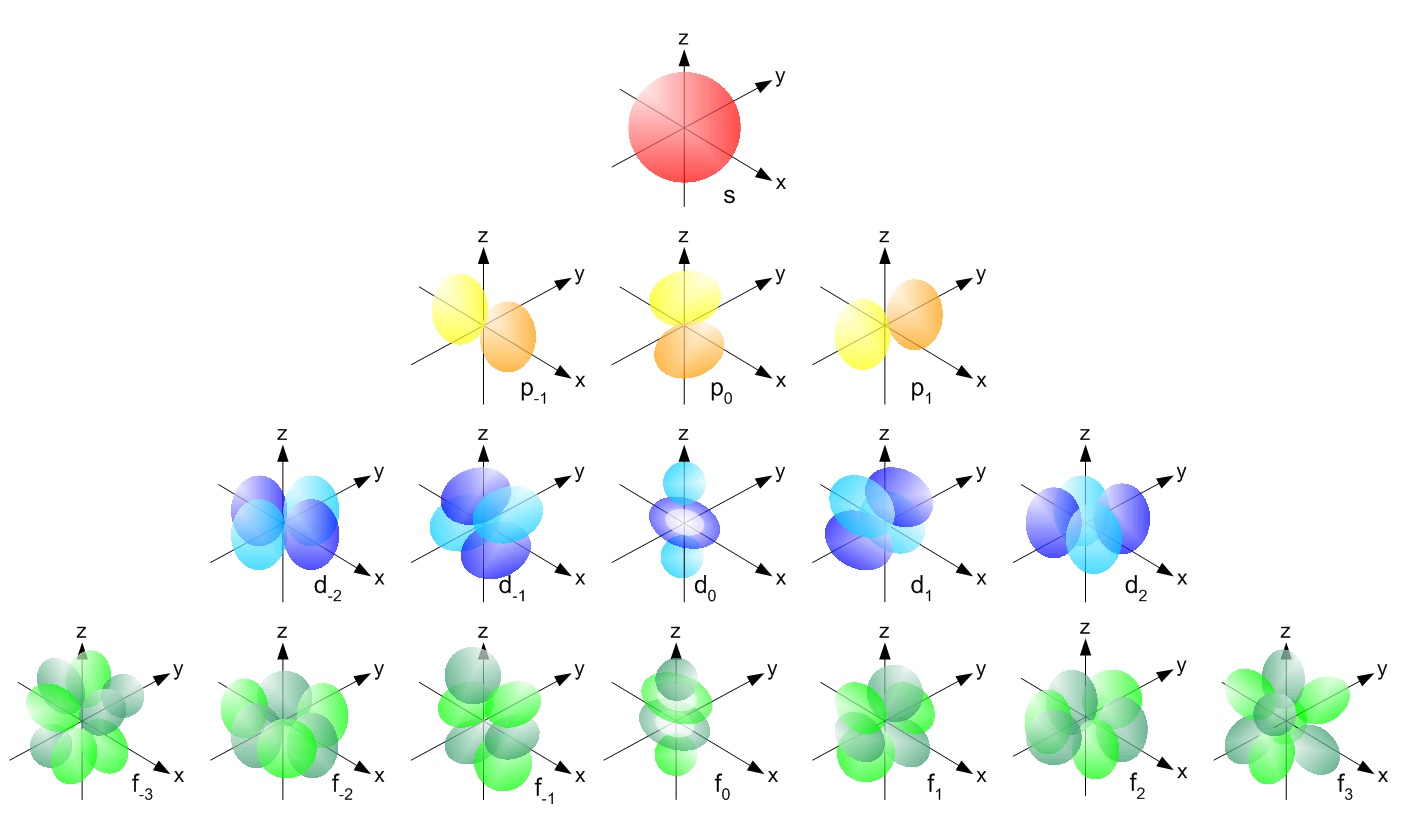
Radial and Angular Nodes
There are two types of nodes, angular and radial nodes. Angular nodes are typically flat plane (at fixed angles), like those in the diagram above. The ℓ quantum number determines the number of angular nodes in an orbital. Radial nodes are spheres (at fixed radius) that occurs as the principal quantum number increases. The total nodes of an orbital is the sum of angular and radial nodes and is given in terms of the \(n\) and \(l\) quantum number by the following equation:
\[ N = n-l -1\]

For example, determine the nodes in the 3pz orbital, given that n = 3 and ℓ = 1 (because it is a p orbital). The total number of nodes present in this orbital is equal to n-1. In this case, 3-1=2, so there are 2 total nodes. The quantum number ℓ determines the number of angular nodes; there is 1 angular node, specifically on the xy plane because this is a pz orbital. Because there is one node left, there must be one radial node. To sum up, the 3pz orbital has 2 nodes: 1 angular node and 1 radial node. This is demonstrated in Figure 2.
Another example is the 5dxy orbital. There are four nodes total (5-1=4) and there are two angular nodes (d orbital has a quantum number ℓ=2) on the xz and zy planes. This means there there must be two radial nodes. The number of radial and angular nodes can only be calculated if the principal quantum number, type of orbital (s,p,d,f), and the plane that the orbital is resting on (x,y,z, xy, etc.) are known.
Electron Configuration within an Orbital
We can think of an atom like a hotel. The nucleus is the lobby where the protons and neutrons are, and in the floors above, we find the rooms (orbitals) with the electrons. The principal quantum number is the floor number, the subshell type lets us know what type of room it is (s being a closet, p being a single room, d having two adjoining rooms, and f being a suit with three rooms) , the magnetic quantum number lets us know how many beds there are in the room, and two electrons can sleep in one bed (this is because each has a different spin; -1/2 and 1/2). For example, on the first floor we have the s orbital. The s orbital is a closet and has one bed in it so the first floor can hold a total of two electrons. The second floor has the room styles s and p. The s is a closet with one bed as we know and the p room is a single with three beds in it so the second floor can hold a total of 8 electrons.
Each orbital, as previously mentioned, has its own energy level associated to it. The lowest energy level electron orbitals are filled first and if there are more electrons after the lowest energy level is filled, they move to the next orbital. The order of the electron orbital energy levels, starting from least to greatest, is as follows: 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7p.
Since electrons all have the same charge, they stay as far away as possible because of repulsion. So, if there are open orbitals in the same energy level, the electrons will fill each orbital singly before filling the orbital with two electrons. For example, the 2p shell has three p orbitals. If there are more electrons after the 1s, and 2s orbitals have been filled, each p orbital will be filled with one electron first before two electrons try to reside in the same p orbital. This is known as Hund's rule.
The way electrons move from one orbital to the next is very similar to walking up a flight of stairs. When walking up stairs, you place one foot on the first stair and then another foot on the second stair. At any point in time, you can either stand with both feet on the first stair, or on the second stair but it is impossible to stand in between the two stairs. This is the way electrons move from one electron orbital to the next. Electrons can either jump to a higher energy level by absorbing, or gaining energy, or drop to a lower energy level by emitting, or losing energy. However, electrons will never be found in between two orbitals.
Problems
- Which orbital would the electrons fill first? The 2s or 2p orbital?
- How many d orbitals are there in the d subshell?
- How many electrons can the p orbital hold?
- Determine the number of angular and radial nodes of a 4f orbital.
- What is the shape of an orbital with 4 radial nodes and 1 angular node in the xy plane?
Solutions
- The 2s orbital would be filled before the 2p orbital because orbitals that are lower in energy are filled first. The 2s orbital is lower in energy than the 2p orbital.
- There are 5 d orbitals in the d subshell.
- A p orbital can hold 6 electrons.
- Based off of the given information, n=4 and ℓ=3. Thus, there are 3 angular nodes present. The total number of nodes in this orbital is: 4-1=3, which means there are no radial nodes present.
- 1 angular node means ℓ=1 which tells us that we have a p subshell, specifically the pz orbital because the angular node is on the xy plane. The total number of nodes in this orbital is: 4 radial nodes +1 angular node=5 nodes. To find n, solve the equation: nodes=n-1; in this case, 5=n-1, so n=6. This gives us a: 6pz orbital
References
- General Chemistry Principles & Modern Applications. 9th ed. New Jersey: Pearson Education, Inc, 2007. Print.
- A new Dictionary of Chemistry. 3rd ed. Great Britian: Longman Green & Co., 1961. Print.
- General Chemistry. USA: Linus Pauling, 1947. Print.

