Multi-electron Atoms
- Page ID
- 1652
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Electrons with more than one atom, such as Helium (He), and Nitrogen (N), are referred to as multi-electron atoms. Hydrogen is the only atom in the periodic table that has one electron in the orbitals under ground state. We will learn how additional electrons behave and affect a certain atom.
Introduction
Let's review some basic concepts. First, electrons repel against each other. Particles with the same charge repel each other, while oppositely charged particles attract each other. For example, a proton, which is positively charged, is attracted to electrons, which are negatively charged. However, if we put two electrons together or two protons together, they will repel one another. Since neutrons lack a charge, they will neither repel nor attract protons or electrons.
Figure 1: a) The two electrons are placed together and repel each other because of the same charge. b) The two protons are repelling each other for the same reason. c) When oppositely charged particles, an electron and a proton, are placed together, they attract each other.
Protons and neutrons are located in an atom's nucleus. Electrons float around the atom in energy levels. Energy levels consist of orbitals and sub-orbitals. The lower the energy level the electron is located at, the closer it is to nucleus. As we go down and to the right of the periodic table, the number of electrons that an element has increases. Since there are more electrons, the atom experiences greater repulsion and electrons will tend to stay as far away from each other as possible. Our main focus is what effects take place when more electrons surround the nucleus. To better understand the following concepts it is a good idea to first review quantum mechanics.
Shielding (Screening)
With more protons in the nucleus, the attractive force for electrons to the nucleus is stronger. Thus, the orbital energy becomes more negative (less energy). Orbital energy also depends on the type of l orbital an electron is located in. The lower the number of l, the closer it is to the nucleus. For example, l=0 is the s orbital. S orbitals are closer to the nucleus than the p orbitals (l=1) that are closer to the nucleus than the d orbitals (l=2) that are closer to the f orbitals (l=3).
More electrons create the shielding or screening effect. Shielding or screening means the electrons closer to the nucleus block the outer valence electrons from getting close to the nucleus. See figure 2. Imagine being in a crowded auditorium in a concert. The enthusiastic fans are going to surround the auditorium, trying to get as close to the celebrity on the stage as possible. They are going to prevent people in the back from seeing the celebrity or even the stage. This is the shielding or screening effect. The stage is the nucleus and the celebrity is the protons. The fans are the electrons. Electrons closest to the nucleus will try to be as close to the nucleus as possible. The outer/valence electrons that are farther away from the nucleus will be shielded by the inner electrons. Therefore, the inner electrons prevent the outer electrons from forming a strong attraction to the nucleus. The degree to which the electrons are being screened by inner electrons can be shown by ns<np<nd<nf where n is the energy level. The inner electrons will be attracted to the nucleus much more than the outer electrons. Thus, the attractive forces of the valence electrons to the nucleus are reduced due to the shielding effects. That is why it is easier to remove valence electrons than the inner electrons. It also reduces the nuclear charge of an atom.
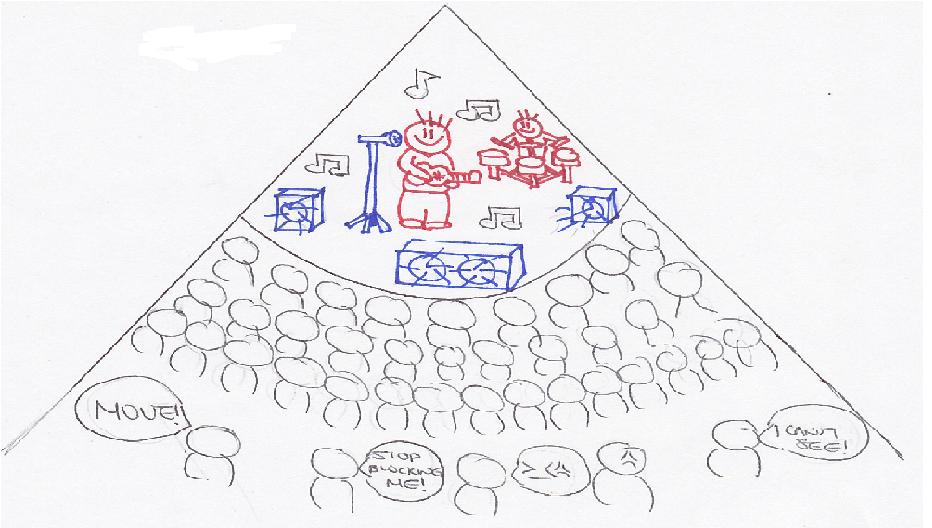
Penetration
Penetration is the ability of an electron to get close to the nucleus. The penetration of ns > np > nd > nf. Thus, the closer the electron is to the nucleus, the higher the penetration. Electrons with higher penetration will shield outer electrons from the nucleus more effectively. The s orbital is closer to the nucleus than the p orbital. Thus, electrons in the s orbital have a higher penetration than electrons in the p orbital. That is why the s orbital electrons shield the electrons from the p orbitals. Electrons with higher penetration are closer to the nucleus than electrons with lower penetration. Electrons with lower penetration are being shielded from the nucleus more.
Radial Probability Distribution
Radial probability distribution is a type of probability to find where an electron is mostly likely going to be in an atom. The higher the penetration, the higher probability of finding an electron near the nucleus. As shown by the graphs, electrons of the s orbital are found closer to the nucleus than the p orbital electrons. Likewise, the lower the energy level an electron is located at, the higher chance it has of being found near the nucleus. The smaller the energy level (n) and the orbital angular momentum quantum number (l) of an electron is, the more likely it will be near the nucleus. As electrons get to higher and higher energy levels, the harder it is to locate it because the radius of the sphere is greater. Thus, the probability of locating an electron will be more difficult. Radial probability distribution can be found by multiplying 4πr², the area of a sphere with a radius of r and R²(r).
Radial Probability Distribution = 4πr² X R²(r)
By using the radial probability distribution equation, we can get a better understanding about an electron's behavior, as shown on Figures 3.1-3.3.
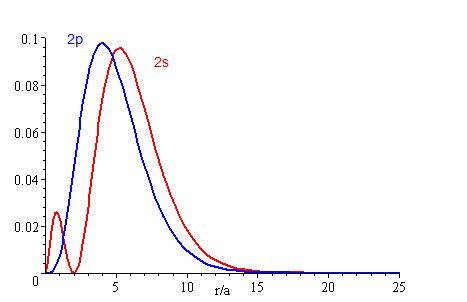
Figures 3.1, 3.2, and 3.3 show that the lower the energy level, the higher the probability of finding the electron close to the nucleus. Also, the lower momentum quantum number gets, the closer it is to the nucleus.
Contributors and Attributions
- Mixue (Michelle) Xie (UCD)

