5.1: Gas Pressure, Temperature, Volume, and Chemical Amount

Learning Objectives

• Define the property of pressure
• Define and convert among the units of pressure measurements
• Identify the mathematical relationships between the various properties of gases
• Use these mathematical relationships to compute the values of various gas properties under specified conditions

Introduction to Pressure

The earth’s atmosphere exerts a pressure, as does any other gas. Although we do not normally notice atmospheric pressure, we are sensitive to pressure changes—for example, when your ears “pop” during take-off and landing while flying, or when you dive underwater. Gas pressure is caused by the force exerted by gas molecules colliding with the surfaces of objects (Figure \(\PageIndex{1}\)). Although the force of each collision is very small, any surface of appreciable area experiences a large number of collisions in a short time, which can result in a large force. In fact, normal air pressure is strong enough to crush a metal container when not balanced by equal pressure from inside the container.

Figure \(\PageIndex{1}\): The atmosphere above us exerts a large pressure on objects at the surface of the earth, roughly equal to the weight of a bowling ball pressing on an area the size of a human thumbnail.

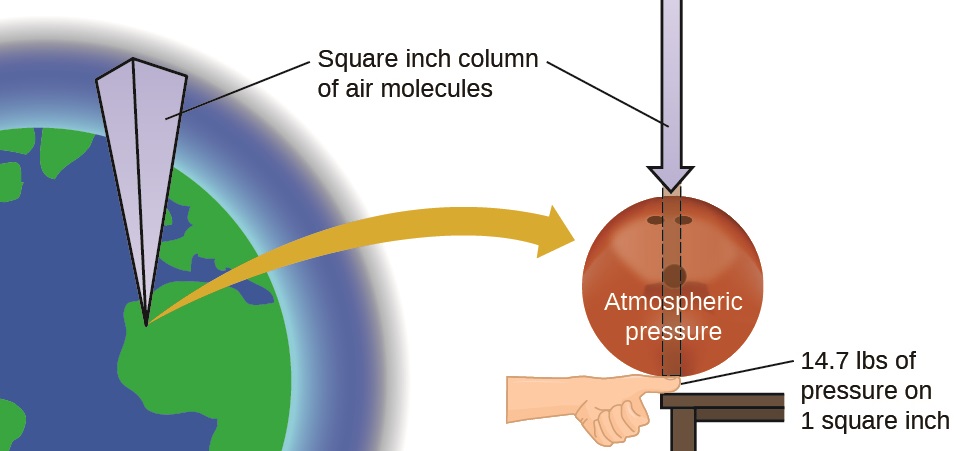
Atmospheric pressure is caused by the weight of the column of air molecules in the atmosphere above an object, such as the tanker car shown in Figure \(\PageIndex{2}\). At sea level, this pressure is roughly the same as that exerted by a full-grown African elephant standing on a doormat, or a typical bowling ball resting on your thumbnail. These may seem like huge amounts, and they are, but life on earth has evolved under such atmospheric pressure. If you actually perch a bowling ball on your thumbnail, the pressure experienced is twice the usual pressure, and the sensation is unpleasant.

 

Figure \(\PageIndex{2}\): A dramatic illustration of atmospheric pressure is provided in this brief video, which shows a railway tanker car imploding when its internal pressure is decreased.

 

Pressure is defined as the force exerted on a given area:

\[P=\dfrac{F}{A}\]

Since pressure is directly proportional to force and inversely proportional to area, pressure can be increased either by either increasing the amount of force or by decreasing the area over which it is applied. Correspondingly, pressure can be decreased by either decreasing the force or increasing the area.

Let’s apply the definition of pressure to determine which would be more likely to fall through thin ice in Figure \(\PageIndex{3}\).—the elephant or the figure skater?

Figure \(\PageIndex{3}\): Although (a) an elephant’s weight is large, creating a very large force on the ground, (b) the figure skater exerts a much higher pressure on the ice due to the small surface area of her skates. (credit a: modification of work by Guido da Rozze; credit b: modification of work by Ryosuke Yagi).

A large African elephant can weigh 7 tons, supported on four feet, each with a diameter of about 1.5 ft (footprint area of 250 in²), so the pressure exerted by each foot is about 14 lb/in²:

\[\mathrm{pressure\: per\: elephant\: foot=14,000\dfrac{lb}{elephant}×\dfrac{1\: elephant}{4\: feet}×\dfrac{1\: foot}{250\:in^2}=14\:lb/in^2} \label{9.2.2}\]

The figure skater weighs about 120 lbs, supported on two skate blades, each with an area of about 2 in², so the pressure exerted by each blade is about 30 lb/in²:

\[\mathrm{pressure\: per\: skate\: blade=120\dfrac{lb}{skater}×\dfrac{1\: skater}{2\: blades}×\dfrac{1\: blade}{2\:in^2}=30\:lb/in^2} \label{9.2.3}\]

Even though the elephant is more than one hundred times heavier than the skater, it exerts less than one-half of the pressure and would therefore be less likely to fall through thin ice. On the other hand, if the skater removes her skates and stands with bare feet (or regular footwear) on the ice, the larger area over which her weight is applied greatly reduces the pressure exerted:

\[\mathrm{pressure\: per\: human\: foot=120\dfrac{lb}{skater}×\dfrac{1\: skater}{2\: feet}×\dfrac{1\: foot}{30\:in^2}=2\:lb/in^2} \label{9.2.4}\]

The SI unit of pressure is the pascal (Pa), with 1 Pa = 1 N/m², where N is the newton, a unit of force defined as 1 kg m/s². One pascal is a small pressure; in many cases, it is more convenient to use units of kilopascal (1 kPa = 1000 Pa) or bar (1 bar = 100,000 Pa). In the United States, pressure is often measured in pounds of force on an area of one square inch—pounds per square inch (psi)—for example, in car tires. Pressure can also be measured using the unit atmosphere (atm), which originally represented the average sea level air pressure at the approximate latitude of Paris (45°). Table \(\PageIndex{1}\) provides some information on these and a few other common units for pressure measurements

Table \(\PageIndex{1}\): Pressure Units

Unit Name and Abbreviation	Definition or Relation to Other Unit	Comment
pascal (Pa)	1 Pa = 1 N/m^2	recommended IUPAC unit
kilopascal (kPa)	1 kPa = 1000 Pa
pounds per square inch (psi)	air pressure at sea level is ~14.7 psi
atmosphere (atm)	1 atm = 101,325 Pa	air pressure at sea level is ~1 atm
bar (bar, or b)	1 bar = 100,000 Pa (exactly)	commonly used in meteorology
millibar (mbar, or mb)	1000 mbar = 1 bar
inches of mercury (in. Hg)	1 in. Hg = 3386 Pa	used by aviation industry, also some weather reports
torr	\(\mathrm{1\: torr=\dfrac{1}{760}\:atm}\)	named after Evangelista Torricelli, inventor of the barometer
millimeters of mercury (mm Hg)	1 mm Hg ~1 torr

Example \(\PageIndex{1}\): Conversion of Pressure Units

The United States National Weather Service reports pressure in both inches of Hg and millibars. Convert a pressure of 29.2 in. Hg into:

1. torr
2. atm
3. kPa
4. mbar

Solution

This is a unit conversion problem. The relationships between the various pressure units are given in Table 9.2.1.

1. \(\mathrm{29.2\cancel{in\: Hg}×\dfrac{25.4\cancel{mm}}{1\cancel{in}} ×\dfrac{1\: torr}{1\cancel{mm\: Hg}} =742\: torr}\)
2. \(\mathrm{742\cancel{torr}×\dfrac{1\: atm}{760\cancel{torr}}=0.976\: atm}\)
3. \(\mathrm{742\cancel{torr}×\dfrac{101.325\: kPa}{760\cancel{torr}}=98.9\: kPa}\)
4. \(\mathrm{98.9\cancel{kPa}×\dfrac{1000\cancel{Pa}}{1\cancel{kPa}} \times \dfrac{1\cancel{bar}}{100,000\cancel{Pa}} \times\dfrac{1000\: mbar}{1\cancel{bar}}=989\: mbar}\)

 

Exercise \(\PageIndex{1}\)

A bicycle tire is inflated to a pressure of 65 psi.  Convert this pressure to atm, torr, and Pa.

Answer

4.4 atm, 3361 torr, 4.5 x 10⁵ Pa

 

Application: Measuring Blood Pressure

Blood pressure is measured using a device called a sphygmomanometer (Greek sphygmos = “pulse”). It consists of an inflatable cuff to restrict blood flow, a manometer to measure the pressure, and a method of determining when blood flow begins and when it becomes impeded (Figure \(\PageIndex{4}\)). Since its invention in 1881, it has been an essential medical device. There are many types of sphygmomanometers: manual ones that require a stethoscope and are used by medical professionals; mercury ones, used when the most accuracy is required; less accurate mechanical ones; and digital ones that can be used with little training but that have limitations. When using a sphygmomanometer, the cuff is placed around the upper arm and inflated until blood flow is completely blocked, then slowly released. As the heart beats, blood forced through the arteries causes a rise in pressure. This rise in pressure at which blood flow begins is the systolic pressure—the peak pressure in the cardiac cycle. When the cuff’s pressure equals the arterial systolic pressure, blood flows past the cuff, creating audible sounds that can be heard using a stethoscope. This is followed by a decrease in pressure as the heart’s ventricles prepare for another beat. As cuff pressure continues to decrease, eventually sound is no longer heard; this is the diastolic pressure—the lowest pressure (resting phase) in the cardiac cycle. Blood pressure units from a sphygmomanometer are in terms of millimeters of mercury (mm Hg).

Figure \(\PageIndex{4}\): (a) A medical technician prepares to measure a patient’s blood pressure with a sphygmomanometer. (b) A typical sphygmomanometer uses a valved rubber bulb to inflate the cuff and a diaphragm gauge to measure pressure. (credit a: modification of work by Master Sgt. Jeffrey Allen)

 

Pressure, Volume, Temperature, and amount of substance

During the seventeenth and especially eighteenth centuries, driven both by a desire to understand nature and a quest to make balloons in which they could fly (Figure \(\PageIndex{5}\)), a number of scientists established the relationships between the macroscopic physical properties of gases, that is, pressure, volume, temperature, and amount of gas. Although their measurements were not precise by today’s standards, they were able to determine the mathematical relationships between pairs of these variables (e.g., pressure and temperature, pressure and volume) that hold for an ideal gas—a hypothetical construct that real gases approximate under certain conditions. Eventually, these individual laws were combined into a single equation—the ideal gas law—that relates gas quantities for gases and is quite accurate for low pressures and moderate temperatures. We will consider the key developments in individual relationships (for pedagogical reasons not quite in historical order), then put them together in the ideal gas law.

Figure \(\PageIndex{5}\): In 1783, the first (a) hydrogen-filled balloon flight, (b) manned hot air balloon flight, and (c) manned hydrogen-filled balloon flight occurred. When the hydrogen-filled balloon depicted in (a) landed, the frightened villagers of Gonesse reportedly destroyed it with pitchforks and knives. The launch of the latter was reportedly viewed by 400,000 people in Paris.

 

Pressure and Temperature: Amontons’s Law

Imagine filling a rigid container attached to a pressure gauge with gas and then sealing the container so that no gas may escape. If the container is cooled, the gas inside likewise gets colder and its pressure is observed to decrease. Since the container is rigid and tightly sealed, both the volume and number of moles of gas remain constant. If we heat the sphere, the gas inside gets hotter (Figure \(\PageIndex{6}\)) and the pressure increases.

Figure \(\PageIndex{6}\): The effect of temperature on gas pressure: When the hot plate is off, the pressure of the gas in the sphere is relatively low. As the gas is heated, the pressure of the gas in the sphere increases.

 

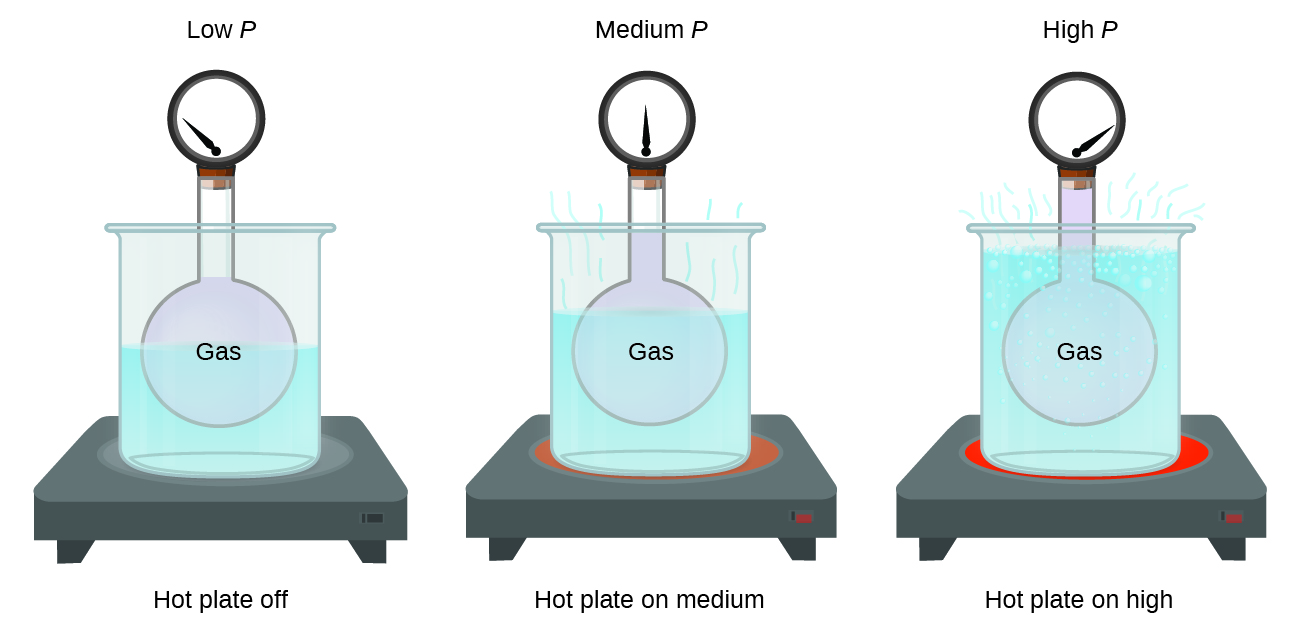
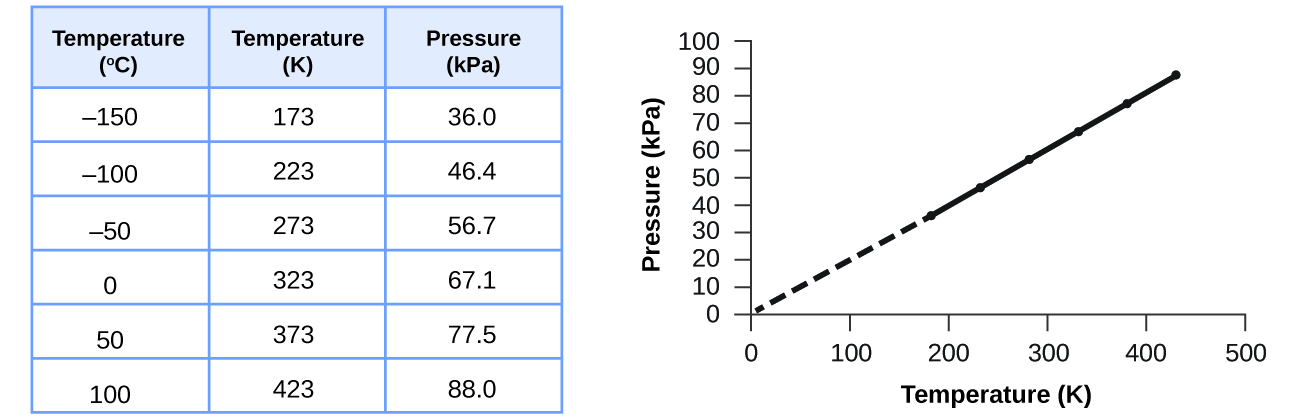
This relationship between temperature and pressure is observed for any sample of gas confined to a constant volume. An example of experimental pressure-temperature data is shown for a sample of air under these conditions in Figure \(\PageIndex{7}\).  The table in  Figure \(\PageIndex{7}\) is a useful summary of the experimemental data, but the graph is a very efficient way to show the relationship between pressure and temperature. Since this shows temperature and pressure are linearly related, the data for these two properties must fit a linear equation.  Notice that with the temperature in kelvin, the pressure goes to zero at 0 K.  P and T are directly proportional when volume and moles of gas are held constant; doubling the temperature will double the pressure.

Figure \(\PageIndex{7}\): For a constant volume and amount of air, the pressure and temperature are directly proportional, provided the temperature is in kelvin. (Measurements cannot be made at lower temperatures because of the condensation of the gas.) When this line is extrapolated to lower pressures, it reaches a pressure of 0 at –273 °C, which is 0 on the kelvin scale and the lowest possible temperature, called absolute zero.

 

Guillaume Amontons was the first to empirically establish the relationship between the pressure and the temperature of a gas (~1700), and Joseph Louis Gay-Lussac determined the relationship more precisely (~1800). Because of this, the P-T relationship for gases is known as either Amontons’s law or Gay-Lussac’s law. Under either name, it states that the pressure of a given amount of gas is directly proportional to its temperature on the kelvin scale when the volume is held constant. Mathematically, this can be written:

\[P∝T\ce{\:or\:}P=\ce{constant}×T\ce{\:or\:}P=k×T \nonumber \]

where ∝ means “is proportional to,” and k is a proportionality constant that depends on the identity, amount, and volume of the gas.

For a confined, constant volume of gas, the ratio \(\dfrac{P}{T}\) is therefore constant (i.e., \(\dfrac{P}{T}=k\)). If the gas is initially in “Condition 1” (with P = P₁ and T = T₁), and then changes to “Condition 2” (with P = P₂ and T = T₂), we have that \(\dfrac{P_1}{T_1}=k\) and \(\dfrac{P_2}{T_2}=k\), which reduces to \(\dfrac{P_1}{T_1}=\dfrac{P_2}{T_2}\). This equation is useful for pressure-temperature calculations for a confined gas at constant volume. Note that temperatures must be on the kelvin scale for any gas law calculations.  This is critical because the kelvin scale is an absolute scale where 0 K is the lowest possible temperature.  Gas law calculations would not make sense in a temperature scale with negative temperatures - like the Farenheit scale. 

Example \(\PageIndex{2}\): Predicting Change in Pressure with Temperature

A can of hair spray is used until it is empty except for the propellant, isobutane gas.

1. On the can is the warning “Store only at temperatures below 120 °F (48.8 °C). Do not incinerate.” Why?
2. The gas in the can is initially at 24 °C and 360 kPa, and the can has a volume of 350 mL. If the can is left in a car that reaches 50 °C on a hot day, what is the new pressure in the can?

Solution

1. The can contains an amount of isobutane gas at a constant volume, so if the temperature is increased by heating, the pressure will increase proportionately. High temperature causes high pressure, and the can will burst. Since, isobutane is combustible incineration can also cause the contents of the can to explode.
2. We are looking for a pressure change due to a temperature change at constant volume, so we will use Amontons’s/Gay-Lussac’s law. Taking P₁ and T₁ as the initial values, T₂ as the temperature where the pressure is unknown and P₂ as the unknown pressure, and converting °C to K, we have:

\(\dfrac{P_1}{T_1}=\dfrac{P_2}{T_2}\textrm{ which means that }\dfrac{360\:\ce{kPa}}{297\:\ce K}=\dfrac{P_2}{323\:\ce K}\)

Rearranging and solving gives:

\(P_2=\mathrm{\dfrac{360\:kPa×323\cancel{K}}{297\cancel{K}}=390\:kPa}\)

 

Exercise \(\PageIndex{2}\)

A sample of nitrogen, N₂, occupies 45.0 mL at 27 °C and 600 torr. What pressure will it have if cooled to –73 °C while the volume remains constant?

Answer

400 torr

 

Volume and Temperature: Charles’s Law

If we fill a balloon with air and seal it, the balloon contains a specific amount of air at atmospheric pressure, let’s say 1 atm. If we put the balloon in a refrigerator, the gas inside gets cold and the balloon shrinks (although both the amount of gas and its pressure remain constant). If we make the balloon very cold, it will shrink a great deal, and it expands again when it warms up.

Video \(\PageIndex{1}\): This video shows how cooling and heating a gas causes its volume to decrease or increase, respectively.

These examples of the effect of temperature on the volume of a given amount of a confined gas at constant pressure are true in general: The volume increases as the temperature increases, and decreases as the temperature decreases. Volume-temperature data for a 1-mole sample of methane gas at 1 atm are listed and graphed in Figure \(\PageIndex{8}\).

Figuire \(\PageIndex{8}\): The volume and temperature are linearly related for 1 mole of methane gas at a constant pressure of 1 atm. If the temperature is in kelvin, volume and temperature are directly proportional. The line stops at 111 K because methane liquefies at this temperature; when extrapolated, it intersects the graph’s origin, representing a temperature of absolute zero.

 

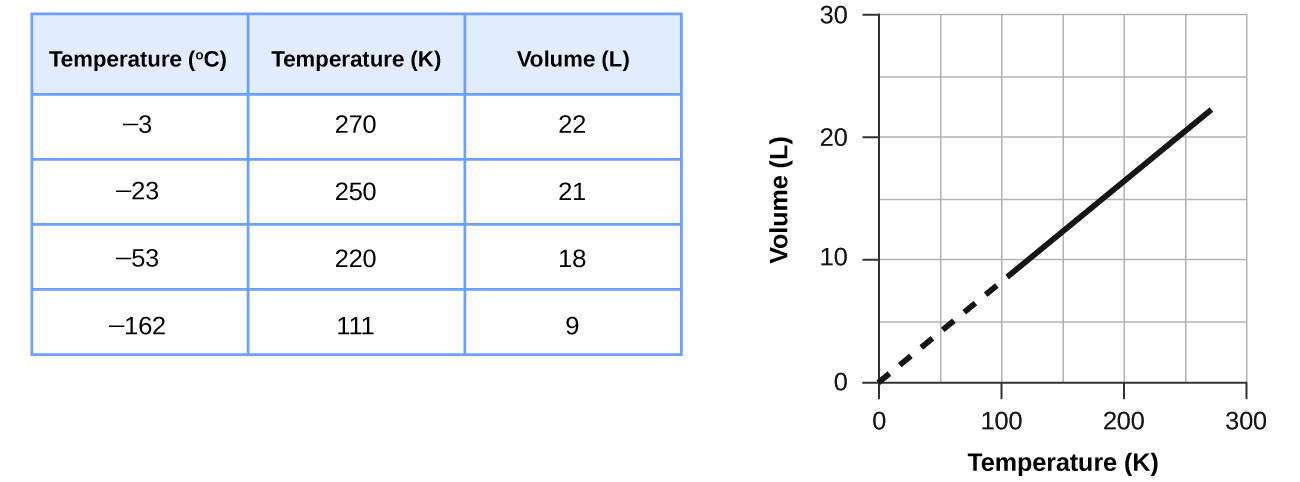
The relationship between the volume and temperature of a given amount of gas at constant pressure is known as Charles’s law in recognition of the French scientist and balloon flight pioneer Jacques Alexandre César Charles. Charles’s law states that the volume of a given amount of gas is directly proportional to its temperature on the kelvin scale when the pressure is held constant.

Mathematically, this can be written as:

\[VαT\ce{\:or\:}V=\ce{constant}·T\ce{\:or\:}V=k·T \nonumber \]

with k being a proportionality constant that depends on the amount and pressure of the gas.

For a confined, constant pressure gas sample, \(\dfrac{V}{T}\) is constant (i.e., the ratio = k), and as seen with the P-T relationship, this leads to another form of Charles’s law: \(\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}\).

Example \(\PageIndex{3}\): Predicting Change in Volume with Temperature

A sample of carbon dioxide, CO₂, occupies 0.300 L at 10 °C and 750 torr. What volume will the gas have at 30 °C and 750 torr?

Solution

Because we are looking for the volume change caused by a temperature change at constant pressure, this is a job for Charles’s law. Taking V₁ and T₁ as the initial values, T₂ as the temperature at which the volume is unknown and V₂ as the unknown volume, and converting °C into K we have:

\(\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}\textrm{ which means that }\dfrac{0.300\:\ce L}{283\:\ce K}=\dfrac{V_2}{303\:\ce K}\)

 

Rearranging and solving gives: \(V_2=\mathrm{\dfrac{0.300\:L×303\cancel{K}}{283\cancel{K}}=0.321\:L}\)

This answer supports our expectation from Charles’s law, namely, that raising the gas temperature (from 283 K to 303 K) at a constant pressure will yield an increase in its volume (from 0.300 L to 0.321 L).

 

Exercise \(\PageIndex{3}\)

A sample of oxygen, O₂, occupies 32.2 mL at 30 °C and 452 torr. What volume will it occupy at –70 °C and the same pressure?

Answer

21.6 mL

Example \(\PageIndex{4}\): Measuring Temperature with a Volume

Change Temperature is sometimes measured with a gas thermometer by observing the change in the volume of the gas as the temperature changes at constant pressure. The hydrogen in a particular hydrogen gas thermometer has a volume of 150.0 cm³ when immersed in a mixture of ice and water (0.00 °C). When immersed in boiling liquid ammonia, the volume of the hydrogen, at the same pressure, is 131.7 cm³. Find the temperature of boiling ammonia on the kelvin and Celsius scales.

Solution

A volume change caused by a temperature change at constant pressure means we should use Charles’s law. Taking V₁ and T₁ as the initial values, T₂ as the temperature at which the volume is unknown and V₂ as the unknown volume, and converting °C into K we have:

\[\dfrac{V_1}{T_1}=\dfrac{V_2}{T_2}\textrm{ which means that }\mathrm{\dfrac{150.0\:cm^3}{273.15\:K}}=\dfrac{131.7\:\ce{cm}^3}{T_2} \nonumber \]

Rearrangement gives \(T_2=\mathrm{\dfrac{131.7\cancel{cm}^3×273.15\:K}{150.0\:cm^3}=239.8\:K}\)

Subtracting 273.15 from 239.8 K, we find that the temperature of the boiling ammonia on the Celsius scale is –33.4 °C.

Exercise \(\PageIndex{4}\)

What is the volume of a sample of ethane at 467 K and 1.1 atm if it occupies 405 mL at 298 K and 1.1 atm?

Answer

635 mL

 

Volume and Pressure: Boyle’s Law

If we partially fill an airtight syringe with air, the syringe contains a specific amount of air at constant temperature, say 25 °C. If we slowly push in the plunger while keeping temperature constant, the gas in the syringe is compressed into a smaller volume and its pressure increases; if we pull out the plunger, the volume increases and the pressure decreases. This example of the effect of volume on the pressure of a given amount of a confined gas is true in general. Decreasing the volume of a contained gas will increase its pressure, and increasing its volume will decrease its pressure. In fact, if the volume increases by a certain factor, the pressure decreases by the same factor, and vice versa. Volume-pressure data for an air sample at room temperature are graphed in Figure \(\PageIndex{9}\).

 

 

Figure \(\PageIndex{9}\): When a gas occupies a smaller volume, it exerts a higher pressure; when it occupies a larger volume, it exerts a lower pressure (assuming the amount of gas and the temperature do not change). Since P and V are inversely proportional, a graph of \(\dfrac{1}{P}\) vs. V is linear.

 

Unlike the P-T and V-T relationships, pressure and volume are not directly proportional to each other. Instead, \(P\) and \(V\) exhibit inverse proportionality: Increasing the pressure results in a decrease of the volume of the gas. Mathematically this can be written:

\[P \propto \dfrac{1}{V} \nonumber \]

or

\[P=k⋅ \dfrac{1}{V} \nonumber \]

or

\[PV=k \nonumber \]

or

\[P_1V_1=P_2V_2 \nonumber \]

with \(k\) being a constant. Graphically, this relationship is shown by the straight line that results when plotting the inverse of the pressure \(\left(\dfrac{1}{P}\right)\) versus the volume (V), or the inverse of volume \(\left(\dfrac{1}{V}\right)\) versus the pressure (\(P\)). Graphs with curved lines are difficult to read accurately at low or high values of the variables, and they are more difficult to use in fitting theoretical equations and parameters to experimental data. For those reasons, scientists often try to find a way to “linearize” their data. If we plot P versus V, we obtain a hyperbola (Figure \(\PageIndex{10}\)).

Figure \(\PageIndex{10}\): The relationship between pressure and volume is inversely proportional. (a) The graph of P vs. V is a hyperbola, whereas (b) the graph of \(\left(\dfrac{1}{P}\right)\) vs. V is linear.

 

The relationship between the volume and pressure of a given amount of gas at constant temperature was first published by the English natural philosopher Robert Boyle over 300 years ago. It is summarized in the statement now known as Boyle’s law: The volume of a given amount of gas held at constant temperature is inversely proportional to the pressure under which it is measured.

Example \(\PageIndex{5}\): Volume of a Gas Sample

The sample of gas has a volume of 15.0 mL at a pressure of 13.0 psi. Determine the pressure of the gas at a volume of 7.5 mL, using:

1. the P-V graph in Figure \(\PageIndex{9}\)
2. the \(\dfrac{1}{P}\) vs. V graph in Figure \(\PageIndex{9}\)
3. the Boyle’s law equation

Comment on the likely accuracy of each method.

Solution

1. Estimating from the P-V graph gives a value for P somewhere around 27 psi.
2. Estimating from the \(\dfrac{1}{P}\) versus V graph give a value of about 26 psi.
3. From Boyle’s law, we know that the product of pressure and volume (PV) for a given sample of gas at a constant temperature is always equal to the same value. Therefore we have P₁V₁ = k and P₂V₂ = k which means that P₁V₁ = P₂V₂.

Using P₁ and V₁ as the known values 13.0 psi and 15.0 mL, P₂ as the pressure at which the volume is unknown, and V₂ as the unknown volume, we have:

\[P_1V_1=P_2V_2\mathrm{\:or\:13.0\:psi×15.0\:mL}=P_2×7.5\:\ce{mL} \nonumber \]

Solving:

\[P_2=\mathrm{\dfrac{13.0\:psi×15.0\cancel{mL}}{7.5\cancel{mL}}=26\:psi} \nonumber \]

It was more difficult to estimate well from the P-V graph, so (a) is likely more inaccurate than (b) or (c). The calculation will be as accurate as the equation and measurements allow.

Exercise \(\PageIndex{5}\)

The sample of gas has a volume of 30.0 mL at a pressure of 6.5 psi. Determine the volume of the gas at a pressure of 11.0 psi, using:

1. the P-V graph in Figure \(\PageIndex{9}\)
2. the \(\dfrac{1}{P}\) vs. V graph in Figure \(\PageIndex{9}\)
3. the Boyle’s law equation

Comment on the likely accuracy of each method.

Answer a

about 17–18 mL

Answer b

~18 mL

Answer c

17.7 mL; it was more difficult to estimate well from the P-V graph, so (a) is likely less accurate than (b); the calculation will be as accurate as the equation and measurements allow

Breathing and Boyle’s Law

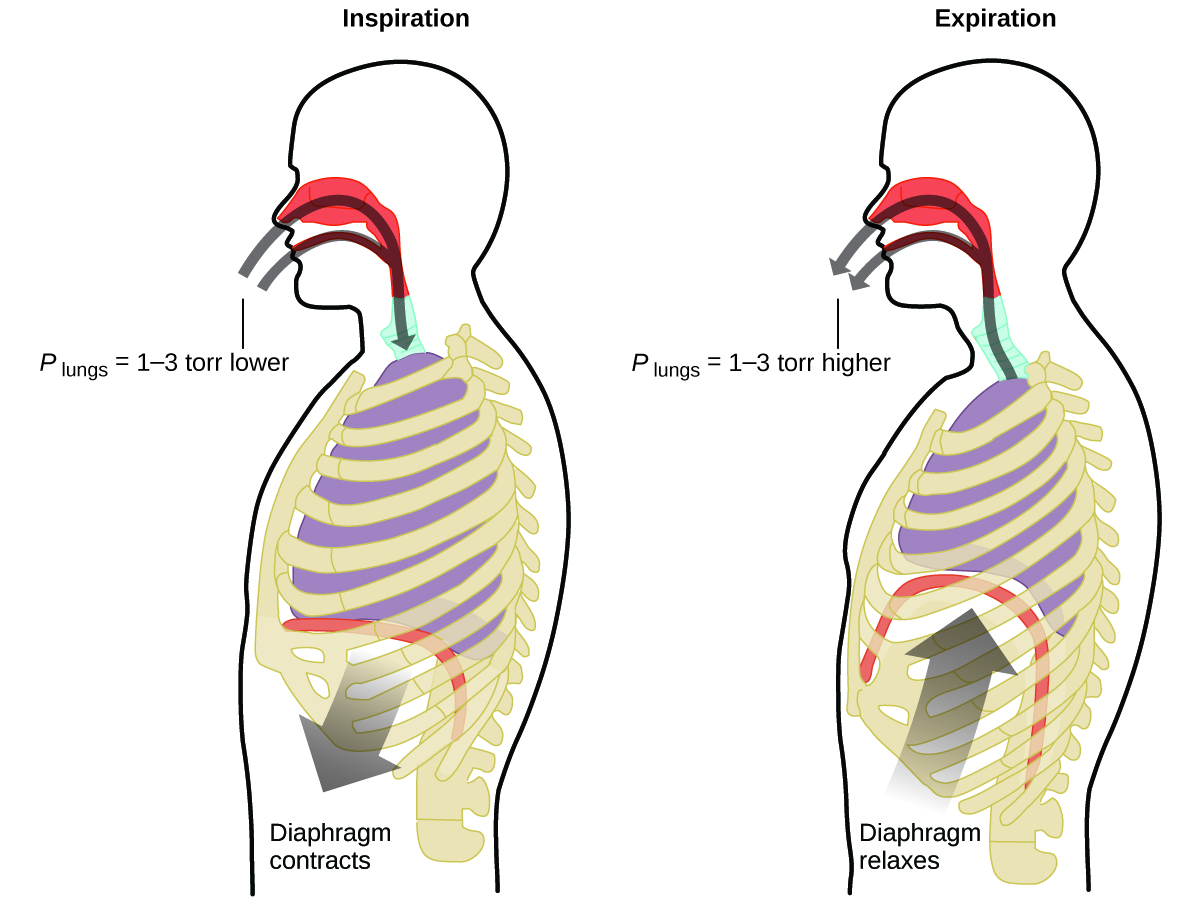
What do you do about 20 times per minute for your whole life, without break, and often without even being aware of it? The answer, of course, is respiration, or breathing. How does it work? It turns out that the gas laws apply here. Your lungs take in gas that your body needs (oxygen) and get rid of waste gas (carbon dioxide). Lungs are made of spongy, stretchy tissue that expands and contracts while you breathe. When you inhale, your diaphragm and intercostal muscles (the muscles between your ribs) contract, expanding your chest cavity and making your lung volume larger. The increase in volume leads to a decrease in pressure (Boyle’s law). This causes air to flow into the lungs (from high pressure to low pressure). When you exhale, the process reverses: Your diaphragm and rib muscles relax, your chest cavity contracts, and your lung volume decreases, causing the pressure to increase (Boyle’s law again), and air flows out of the lungs (from high pressure to low pressure). You then breathe in and out again, and again, repeating this Boyle’s law cycle for the rest of your life (Figure \(\PageIndex{11}\)).

Figure \(\PageIndex{11}\): Breathing occurs because expanding and contracting lung volume creates small pressure differences between your lungs and your surroundings, causing air to be drawn into and forced out of your lungs.

 

 

Moles of Gas and Volume: Avogadro’s Law

The Italian scientist Amedeo Avogadro advanced a hypothesis in 1811 to account for the behavior of gases, stating that equal volumes of all gases, measured under the same conditions of temperature and pressure, contain the same number of molecules. Over time, this relationship was supported by many experimental observations as expressed by Avogadro’s law: For a confined gas, the volume (V) and number of moles (n) are directly proportional if the pressure and temperature both remain constant.

In equation form, this is written as:

\[V∝n\textrm{ or }V=k×n\textrm{ or }\dfrac{V_1}{n_1}=\dfrac{V_2}{n_2} \nonumber \]

Mathematical relationships can also be determined for the other variable pairs, such as P versus n, and n versus T.

Visit this interactive PhET simulation to investigate the relationships between pressure, volume, temperature, and amount of gas. Use the simulation to examine the effect of changing one parameter on another while holding the other parameters constant (as described in the preceding sections on the various gas laws).

 

Summary

Gases exert pressure, which is force per unit area. The pressure of a gas may be expressed in the SI unit of pascal or kilopascal, as well as in many other units including torr, atmosphere, and bar. Atmospheric pressure is measured using a barometer; other gas pressures can be measured using one of several types of manometers.

Key Equations

• \(P=\dfrac{F}{A}\)
• \( \frac{V_1}{n_1}=\frac{V_2}{n_2} \)
• \( P_1 V_1=P_2 V_2 \)
• \( \frac{V_1}{T_1}=\frac{V_2}{T_2} \)
• \( \frac{P_1}{T_1}=\frac{P_2}{T_2} \)

Glossary

atmosphere (atm)

unit of pressure; 1 atm = 101,325 Pa

bar

(bar or b) unit of pressure; 1 bar = 100,000 Pa

barometer

device used to measure atmospheric pressure

hydrostatic pressure

pressure exerted by a fluid due to gravity

manometer

device used to measure the pressure of a gas trapped in a container

pascal (Pa)

SI unit of pressure; 1 Pa = 1 N/m²

pounds per square inch (psi)

unit of pressure common in the US

pressure

force exerted per unit area

torr

unit of pressure; \(\mathrm{1\: torr=\dfrac{1}{760}\,atm}\)

Contributors and Attributions

• Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).