Skip to main content
Chemistry LibreTexts

5.2: Relating Pressure, Volume, Amount, and Temperature - The Ideal Gas Law

  1. Last updated
  2. Save as PDF
  • Page ID
    428713

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

     Learning Objectives
    • Identify the mathematical relationships between the various properties of gases
    • Use the ideal gas law to compute the values of various gas properties under specified conditions

    The Ideal Gas Law

    To this point, four separate laws have been discussed that relate pressure, volume, temperature, and the number of moles of the gas:

    • Boyle’s law: PV = constant; at constant T and n
    • Amontons’s law: \(\dfrac{P}{T}\) = constant; at constant V and n
    • Charles’s law: \(\dfrac{V}{T}\) = constant; at constant P and n
    • Avogadro’s law: \(\dfrac{V}{n}\) = constant; at constant P and T

    Combining these four laws yields the ideal gas law, a relation between the pressure, volume, temperature, and number of moles of a gas:

    \[ \frac{P V}{n T}=constant \]

    \[PV=nRT \]

    where P is the pressure of a gas, V is its volume, n is the number of moles of the gas, T is its temperature on the kelvin scale, and R is a constant called the ideal gas constant or the universal gas constant. The units used to express pressure, volume, and temperature will determine the proper form of the gas constant as required by dimensional analysis, the most commonly encountered values being 0.08206 L atm mol–1 K–1 and 8.3145 kPa L mol–1 K–1.

    The ideal gas law is easy to remember and apply in solving problems, as long as you use the proper values and units for the gas constant, R.

    Gases whose properties of P, V, and T are accurately described by the ideal gas law (or the other gas laws) are said to exhibit ideal behavior or to approximate the traits of an ideal gas. An ideal gas is a hypothetical construct that may be used along with kinetic molecular theory to effectively explain the gas laws as will be described in a later module of this chapter. Although all the calculations presented in this module assume ideal behavior, this assumption is only reasonable for gases under conditions of relatively low pressure and high temperature. In the final module of this chapter, a modified gas law will be introduced that accounts for the non-ideal behavior observed for many gases at relatively high pressures and low temperatures.

    The ideal gas equation contains five terms, the gas constant R and the variable properties P, V, n, and T. Specifying any four of these terms will permit use of the ideal gas law to calculate the fifth term as demonstrated in the following example exercises.

    Example \(\PageIndex{1}\): Using the Ideal Gas Law

    Methane, CH4, is being considered for use as an alternative automotive fuel to replace gasoline. One gallon of gasoline could be replaced by 655 g of CH4. What is the volume of this much methane at 25 °C and 745 torr?

    Solution

    The first step is to convert everything to the necessary units

    • \( 655 \mathrm{~g} \; \mathrm{CH}_4 \times\left(\frac{1 \; \mathrm{Mole} \; \mathrm{CH}_4}{16.0 \; \mathrm{~g} \; \mathrm{CH}_4}\right)=40.9 \; \mathrm{mol} \; \mathrm{CH}_4 \nonumber \)
    • \( 25^{\circ} \mathrm{C}+273=298 \mathrm{~K} \nonumber \)
    • \( 745 \;torr \left(\frac{1 \; \mathrm{ATM}}{760 \text { Torr }}\right)=0.980 \; ATM \nonumber \)

    Substitute in these values for the ideal gas equation as:

    \[ V = \frac{\left(40.9 \operatorname{mol} \mathrm{CH}_4\right)\left(0.0821 \frac{\text {L ATM }}{\text {mol K }}\right)(298 \mathrm{~K})}{0.980 \text { ATM }} \]

     

    V = 1021 L

    Exercise \(\PageIndex{1}\)

    Calculate the pressure in bar of 2520 moles of hydrogen gas stored at 27 °C in the 180-L storage tank of a modern hydrogen-powered car.

    Answer

    350 bar

    Combined Gas Law

    If the number of moles of an ideal gas are kept constant while other conditions are changed, we can simplify the ideal gas equation to easily solve many common questions.  This mathematical relationship is called the combined gas law where P1, V1, and T1 describe the initial set of conditions while P2, V2, and T2 describe the final set of conditions.

    \[\dfrac{P_1V_1}{T_1}=\dfrac{P_2V_2}{T_2}\]

    One convenient feature of this equation is that the units for pressure and volume cancel - so as long as you are consistent with both the initial and final conditions you can use this equation without requiring unit conversions.  NOTE: The temperature must still use an absolute scale like kelvin.  

    Example \(\PageIndex{2}\): Using the Combined Gas Law

    When filled with air, a typical scuba tank with a volume of 13.2 L has a pressure of 153 atm (Figure \(\PageIndex{1}\)). If the water temperature is 27 °C, how many liters of air will such a tank provide to a diver’s lungs at a depth of approximately 70 feet in the ocean where the pressure is 3.13 atm?

    This photograph shows a scuba diver underwater with a tank on their back and bubbles ascending from the breathing apparatus.
    Figure \(\PageIndex{1}\): Scuba divers use compressed air to breathe while underwater. (credit: modification of work by Mark Goodchild)
     

    Letting 1 represent the air in the scuba tank and 2 represent the air in the lungs, and noting that body temperature (the temperature the air will be in the lungs) is 37 °C, we have:

    \[\dfrac{P_1V_1}{T_1}=\dfrac{P_2V_2}{T_2}⟶\mathrm{\dfrac{(153\:atm)(13.2\:L)}{(300\:K)}=\dfrac{(3.13\:atm)(\mathit{V}_2)}{(310\:K)}} \nonumber \]

    Solving for V2:

    \[V_2=\mathrm{\dfrac{(153\cancel{atm})(13.2\:L)(310\cancel{K})}{(300\cancel{K})(3.13\cancel{atm})}=667\:L} \nonumber \]

    (Note: Be advised that this particular example is one in which the assumption of ideal gas behavior is not very reasonable, since it involves gases at relatively high pressures and low temperatures. Despite this limitation, the calculated volume can be viewed as a good “ballpark” estimate.)

    Exercise \(\PageIndex{2}\)

    A sample of ammonia is found to occupy 0.250 L under laboratory conditions of 27 °C and 0.850 atm. Find the volume of this sample at 0 °C and 1.00 atm.

    Answer

    0.193 L

    The Interdependence between Ocean Depth and Pressure in Scuba Diving

    Whether scuba diving at the Great Barrier Reef in Australia (shown in Figure \(\PageIndex{2}\)) or in the Caribbean, divers must understand how pressure affects a number of issues related to their comfort and safety.

    This picture shows colorful underwater corals and anemones in hues of yellow, orange, green, and brown, surrounded by water that appears blue in color.
    Figure \(\PageIndex{2}\): Scuba divers, whether at the Great Barrier Reef or in the Caribbean, must be aware of buoyancy, pressure equalization, and the amount of time they spend underwater, to avoid the risks associated with pressurized gases in the body. (credit: Kyle Taylor).
     

    Pressure increases with ocean depth, and the pressure changes most rapidly as divers reach the surface. The pressure a diver experiences is the sum of all pressures above the diver (from the water and the air). Most pressure measurements are given in units of atmospheres, expressed as “atmospheres absolute” or ATA in the diving community: Every 33 feet of salt water represents 1 ATA of pressure in addition to 1 ATA of pressure from the atmosphere at sea level. As a diver descends, the increase in pressure causes the body’s air pockets in the ears and lungs to compress; on the ascent, the decrease in pressure causes these air pockets to expand, potentially rupturing eardrums or bursting the lungs. Divers must therefore undergo equalization by adding air to body airspaces on the descent by breathing normally and adding air to the mask by breathing out of the nose or adding air to the ears and sinuses by equalization techniques; the corollary is also true on ascent, divers must release air from the body to maintain equalization. Buoyancy, or the ability to control whether a diver sinks or floats, is controlled by the buoyancy compensator (BCD). If a diver is ascending, the air in his BCD expands because of lower pressure according to Boyle’s law (decreasing the pressure of gases increases the volume). The expanding air increases the buoyancy of the diver, and she or he begins to ascend. The diver must vent air from the BCD or risk an uncontrolled ascent that could rupture the lungs. In descending, the increased pressure causes the air in the BCD to compress and the diver sinks much more quickly; the diver must add air to the BCD or risk an uncontrolled descent, facing much higher pressures near the ocean floor. The pressure also impacts how long a diver can stay underwater before ascending. The deeper a diver dives, the more compressed the air that is breathed because of increased pressure: If a diver dives 33 feet, the pressure is 2 ATA and the air would be compressed to one-half of its original volume. The diver uses up available air twice as fast as at the surface.

     

    Standard Conditions of Temperature and Pressure

    We have seen that the volume of a given quantity of gas and the number of molecules (moles) in a given volume of gas vary with changes in pressure and temperature. Chemists sometimes make comparisons against a standard temperature and pressure (STP) for reporting properties of gases: 273.15 K (0.00 °C) and 1 bar pressure (100 kPa).  Be aware that prior to 1982 STP was defined at a pressure of 1 atm (101.325 kPa) and this definition is still in common use. At STP, an ideal gas has a volume of about 22.4 L—this is referred to as the standard molar volume (Figure \(\PageIndex{3}\)).

    This figure shows three balloons each filled with H e, N H subscript 2, and O subscript 2 respectively. Beneath the first balloon is the label “4 g of He” Beneath the second balloon is the label, “15 g of N H subscript 2.” Beneath the third balloon is the label “32 g of O subscript 2.” Each balloon contains the same number of molecules of their respective gases.
    Figure \(\PageIndex{3}\): Since the number of moles in a given volume of gas varies with pressure and temperature changes, chemists use standard temperature and pressure (273.15 K and 1 bar or 100 kPa) to report properties of gases.
     

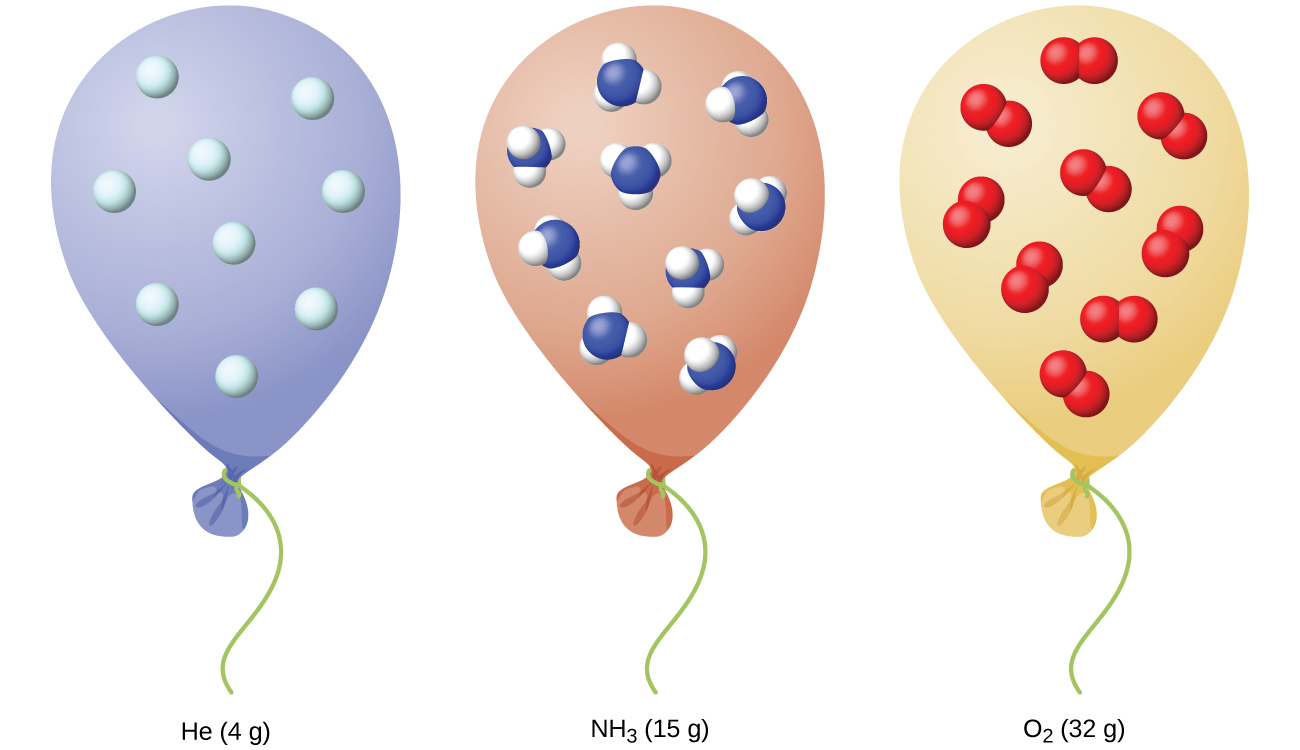
    Summary

    The behavior of gases can be described by several laws based on experimental observations of their properties. The pressure of a given amount of gas is directly proportional to its absolute temperature, provided that the volume does not change (Amontons’s law). The volume of a given gas sample is directly proportional to its absolute temperature at constant pressure (Charles’s law). The volume of a given amount of gas is inversely proportional to its pressure when temperature is held constant (Boyle’s law). Under the same conditions of temperature and pressure, equal volumes of all gases contain the same number of molecules (Avogadro’s law).

    The equations describing these laws are special cases of the ideal gas law, PV = nRT, where P is the pressure of the gas, V is its volume, n is the number of moles of the gas, T is its kelvin temperature, and R is the ideal (universal) gas constant.

    Key Equations

    • PV = nRT

    Summary

    absolute zero
    temperature at which the volume of a gas would be zero according to Charles’s law.
    Amontons’s law
    (also, Gay-Lussac’s law) pressure of a given number of moles of gas is directly proportional to its kelvin temperature when the volume is held constant
    Avogadro’s law
    volume of a gas at constant temperature and pressure is proportional to the number of gas molecules
    Boyle’s law
    volume of a given number of moles of gas held at constant temperature is inversely proportional to the pressure under which it is measured
    Charles’s law
    volume of a given number of moles of gas is directly proportional to its kelvin temperature when the pressure is held constant
    ideal gas
    hypothetical gas whose physical properties are perfectly described by the gas laws
    ideal gas constant (R)
    constant derived from the ideal gas equation R = 0.08226 L atm mol–1 K–1 or 8.314 L kPa mol–1 K–1
    ideal gas law
    relation between the pressure, volume, amount, and temperature of a gas under conditions derived by combination of the simple gas laws
    standard conditions of temperature and pressure (STP)
    273.15 K (0 °C) and 1 bar (100 kPa)
    standard molar volume
    volume of 1 mole of gas at STP, approximately 22.4 L for gases behaving ideally

    This page titled 5.2: Relating Pressure, Volume, Amount, and Temperature - The Ideal Gas Law is shared under a CC BY license and was authored, remixed, and/or curated by Scott Van Bramer.