Magic Angle Hopping (MAH)
- Page ID
- 16966
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Upon the advent of the MAS experiment, solid state NMR became particularly powerful because line shapes that were convoluted and overlapping due to the CSA were able to be resolved. While advantageous, the MAS, assuming the same rotation >> CSA completely averages the CSA, which destroys potentially useful information. The other limitation of MAS is when the CSA>the sample rotation resulting in sideband formation. The Magic Angle Hopping experiment was developed by Bax et al to separate the isotropic contributions of the chemical shift while preserving the anisotropic contributions in a separate dimension. This is accomplished by rotating the sample in successive 120\(^\circ\) increments about the magic angle.
Pulse Sequence
The basic pulse sequence is shown below. It consists of 5 90\(^\circ\) pulses followed by acquisition.
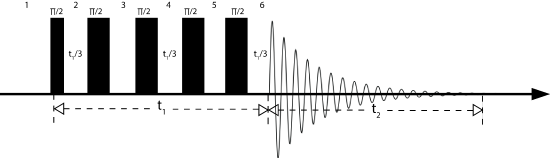
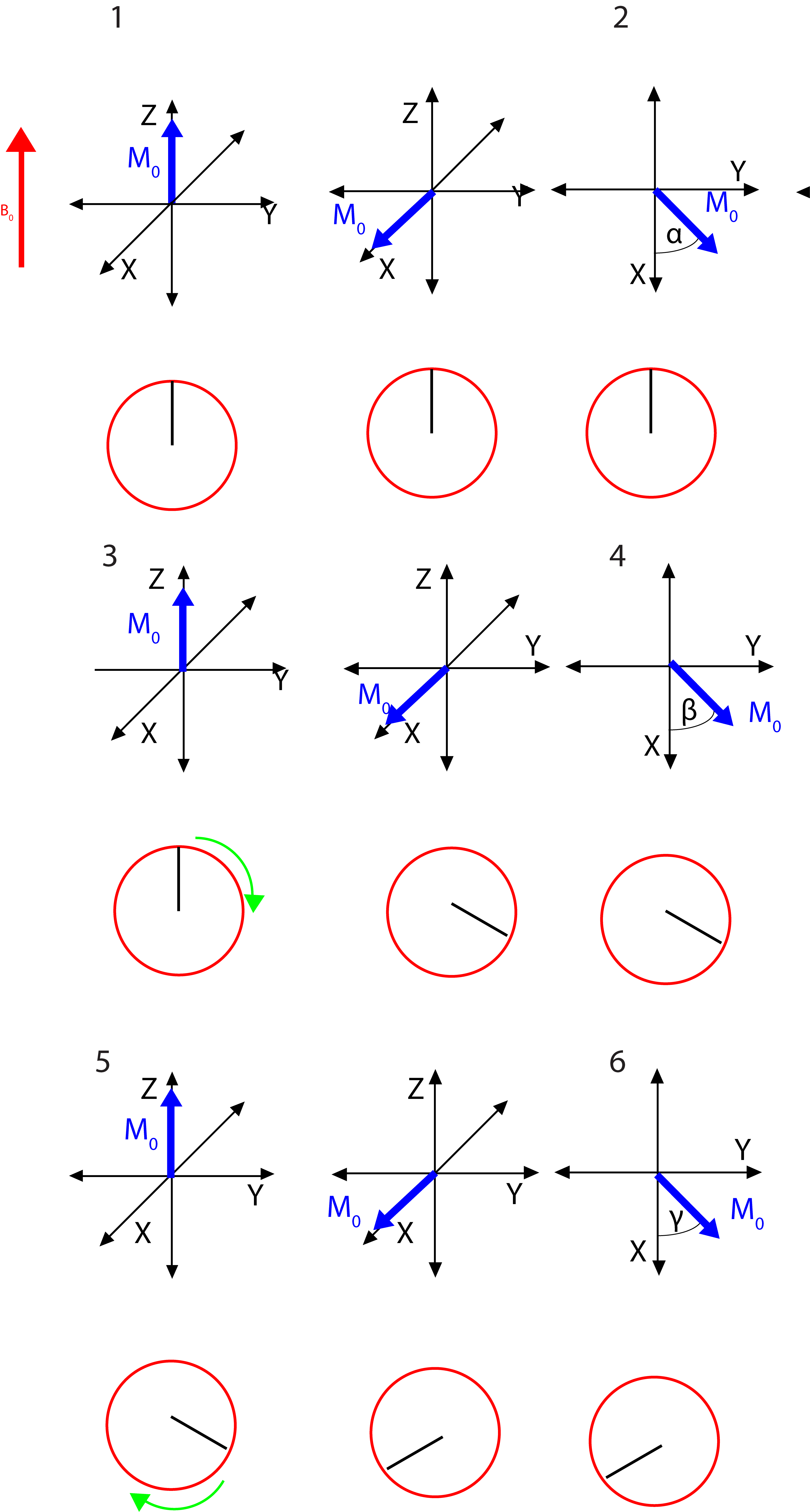
Initially, the bulk magnetization \(M_0\) is along the external magnetic field direction, here the z-axis. This is denoted in the pulse sequence and vector magnetization diagram (below) as 1. The 90\(^\circ\) pulse rotates the magnetization into the x-y plane. (If the pulse is of phase "-y" then the magnetization is along the x-axis!) Next, (2) the magnetization is allowed to process for \(\frac{t_1}{3}\). The angle which the \(M_0\) rotates is \(\alpha\). Application of a 90 \(^\circ\) pulse rotates the magnetization along the z-axis the rotor (depicted by the red circle) is then incremented 120\(^\circ\) (3). Repeating the process of steps 1-3 allows for 1 more evolution period and rotation of 120 \(^\circ\). The rotor is now 240\(^\circ\) from the initial starting position. Finally, the magnetization evolves for one more evolution period until it is detected (6).
The MAH hopping experiment needs 4 experiments per t1 increment in order to completely average the CSA contributions and obtain a pure isotropic dimension. Additionally, the MAH experiment is a 2D experiment in which t1 is incremented to create the second dimension.
Mathematical Treatment of Magnetization Evolution
Lets consider the picture of the vector magnetization. Initially, the magnetization lies along the z-axis (1). Application of a \(\frac{\pi}{2}-y\) pulse places the bulk magnetization, M0 along the x-axis, where it evolves for a period of time (2). The precession in the x-y plane is dependent on the frequency of the individual spin for the given sample orientation and position in the rotor, and the amount of time. More simply,
\[\alpha=\omega_a \frac{t_1}{3}\]
The magnetization is the placed along the z-axis, forcing the transverse magnetization to de-phase and the rotor is incremented 120\(^\circ\). The spin that was initially in position A is now in position B, rotated 120\(^\circ\) about the magic angle (3). Repeating the same process described above we now obtain (4-6)
\[\beta=\omega_b \dfrac{t_1}{3}\]
and
\[\gamma=\omega_c \dfrac{t_1}{3}\]
At the end of t1, the \(x\) component of the magnetization is
\[M_0\cos\alpha \cos\beta \cos\gamma\]
and the total magnetization in the x-y plane becomes
\[M_1(t_1=)M_0 \cos\alpha \cos\beta exp(i\omega_c\frac{t_1}{3})\]
Next the phases of the pulses are incremented in such a way the following magnetization are obtained during t1
\[M_2(t_1)=iM_0\sin\alpha \cos\beta exp(i\omega_c\frac{t_1}{3})\]
\[M_3(t_1)=iM_0 \cos\alpha \sin\beta exp(i\omega_c\frac{t_1}{3})\]
\[M_4(t_1)=-M_0 \sin\alpha \sin\beta exp(i\omega_c\frac{t_1}{3})\]
Using Eulers formula summation of the above equations results in
\[M_0 exp(i{\omega_a+\omega_b+\omega_c}\frac{t_1}{3})\]
where
\[\dfrac{\omega_a+\omega_b+\omega_c}{3}=\dfrac{ Tr \sigma}{3}=\dfrac{(\sigma_{11}+\sigma_{22}+\sigma_{33})}{3}=\omega_{iso}\]
Thus the signal only contains the isotropic shielding resonance frequencies. Consider the sum of the signal to include both t1 and t2, the magnetization is
\[M=M_0exp(i\omega_it_1)exp(i\omega_ct_2)exp(-[t_1+t_2]/T_2)\]
Data Analysis
The CSA components still evolve during t2, which correspond to the static sample. Consequently CSA information is contained in the second dimension. The spectral width of the second dimension is defined by the 1/t1 increment, while the number of points in the second dimension is the number of t1 points. The spectrum below is what one obtains after Fourier Transforming in both dimensions.
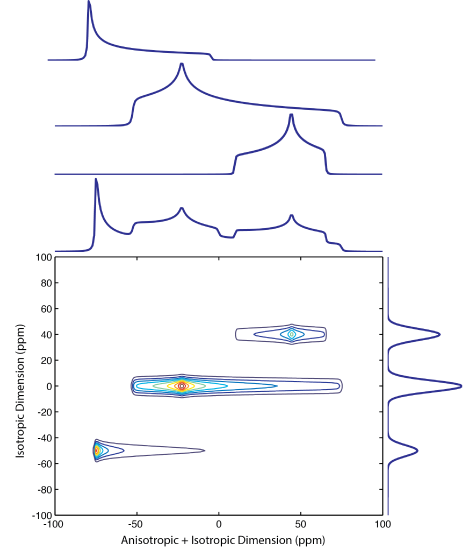
Each CSA pattern may be extracted and simulated to extract the CSA tensor parameters, while fitting the isotropic spectrum will give the relative fractions of each site.
References
1. Bax, A., Szeverenyi, M., Maciel, G. E. Journal of Magnetic Resonance. 52 147-152 (1983)

