Two-photon absorption
- Page ID
- 1776
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Two-photon absorption is one of a variety of two-photon processes. In this specific process, two photons are absorbed by a sample simultaneously. Neither photon is at resonance with the available energy states of the system, however, the combined frequency of the photons is at resonance with an energy state.
Introduction
Two-photon absorption may seem very similar to non-resonance Raman, and was in fact predicted due to this phenomena. In both cases, a non-resonant photon is used for excitation. However, in the absorption case a secondary non-resonant photon is used for excitation as well, while in Raman a second non-resonant photon is emitted. For Raman this results in occupation of an energy state at the difference of the frequencies of the absorbed and emitted photon. However, in two-photon absorption this results in the occupation of an energy state at the sum of the frequencies of the absorbed photons. The basic process is illustrated below in Figure 1.
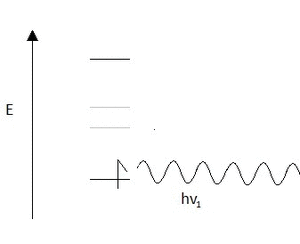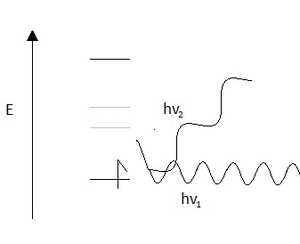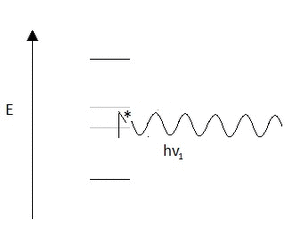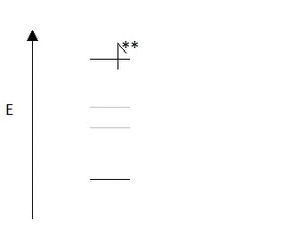
Two-photon absorption is not a feature of a specific type of spectroscopy. It can be utilized in any type of spectroscopy including IR, NMR, XAS, and UV-VIS. However, it will result in a change of selection rules for many of these spectroscopies. This means that the peak shapes should remain the same, but the intensities should be significantly smaller due to the result of the second order perturbation.
History
In her 1931 dissertation, Maria Goeppert-Mayer postulated the existence of two-photon absorption for the first time. She says that she based the derivation of this phenomena off of Kramer and Heisenberg's derivation of the probability of two-photon emission which uses Dirac's dispersion theory for calculation.
The invention of the laser had a great impact on the field of two-photon spectroscopy because of the necessity of a high-intensity electromagnetic field to induce transitions. Although, lasers were not formally invented until 1969, Bell Labs was testing masers in 1958, which were only capable of short pulses of intense electromagnetic radiation. In 1961 Kaiser and Garret reported the first two-photon absorption of a compound. They used the new laser technology to excite CaF\(_{2}\)Eu\(^{2+}\) with both red and blue light to induce a two photon transition.
General Perturbation Method
The following constants, variables, and operators are used in this section:
| \(\hbar\) | Reduced Planck's constant = 1.058x10-34 Js |
| e | Elementary electric charge = 1.602x10-19 Coulombs |
| t | time |
| \(\omega\) | angular frequency |
| \(\hat{H}_{0}\) | \(\frac{\hat{p}^{2}}{2m}\) |
| \(\hat{p}\) | \(-i\hbar\nabla\) |
First we must take a look at how the atomic system interacts with any perturbation
\[ \hat{H} = \hat{H}_{0} + \hat{H}_{1}\hspace{1cm}\label{1}\]
If we are only going to look at the effects of the electric dipole then:
\[ \hat{H} = \hat{H}_{0} + \hat{H}_{\mu_{e}}\hspace{1cm}\label{2}\]
Now we must consider how our states will be evolving in time because the Electric Dipole operator is time-dependent. According to the time-dependent Schrödinger equation:
\[ \Psi_{\textrm{i}}(t) = \textrm{exp}\left (-\frac{i\hat{H}(t-t_{0})}{\hbar}\right )\Psi_{\textrm{i}}(t_{0})\hspace{1cm} \label{3} \]
We have described our ground state as it is moving in time so now we can look at our final state which we can only describe as being at a set energy value:
\[\hat{H}_{0}\Psi_{f} = \hbar\omega_{f}\Psi_{f}\hspace{1cm} \label{4} \]
Now that we have described both the final and the initial states.
We can find the probability of such a transition by finding the magnitude of the projection of the intial state upon the final state, otherwise known as the magnitude of the inner product.
\[ |\left <\Psi_{f}| \Psi_{i}(t) \right >|^{2} =\]
\[ \left | \left <\Psi_{f} \left | \textrm{exp}\left (-\frac{i\hat{H}(t-t_{0})}{\hbar}\right )\right | \Psi_{\textrm{i}}(t_{0}) \right > \right | ^{2}\hspace{1cm} \label{5}\]
Now that we've found the general formula for the probability of our transitions in a time-dependent system, we must apply the perturbation from earlier. To do this we use the following identity:
\[ \textrm{exp} \left (\frac{i\hat{H}_{0}t}{\hbar}\right )\hat{H}_{\mu_{e}}\textrm{exp}\left (-\frac{i\hat{H}t}{\hbar}\right ) = i\hbar\frac{\textrm{d}}{\textrm{d}t}\left [\textrm{exp}\left (\frac{i\hat{H}_{0}t}{\hbar}\right )\textrm{exp}\left (-\frac{i\hat{H}t}{\hbar}\right )\right ] \hspace{1cm}\label{6} \]
The issue now is that the electric dipole Hamiltonian is not in the exponential form, this prevents us from simply solving for the total Hamiltonian exponential. To solve this we integrate with respect to time, which nullifies the derivative.
\[ \int^{t}_{t_{0}} \textrm{exp}\left (\frac{i\hat{H}_{0}t}{\hbar}\right )\hat{H}_{\mu_{e}}\textrm{exp}\left (-\frac{i\hat{H}t}{\hbar}\right ) \textrm{d}t_{1} \]
\[= i\hbar\left [\textrm{exp}\left (\frac{i\hat{H}_{0}t}{\hbar}\right )\textrm{exp}\left (-\frac{i\hat{H}t}{\hbar}\right ) -\textrm{exp}\left (\frac{i\hat{H}_{0}t_{0}}{\hbar}\right )\textrm{exp}\left (-\frac{i\hat{H}t_{0}}{\hbar}\right )\right ]\hspace{1cm} \label{7}\]
This equation can be simplified and solved for using the approximation that the initial time was well before the incident of interaction with the perturbation. This allows us to assume that the electric dipole Hamiltonian would yield 0 at the initial time. This allows for the following iterative equation.
\[ \textrm{exp}\left (\frac{-i\hat{H}t}{\hbar} \right ) = \textrm{exp} \left ( -\frac{i\hat{H}_{0}t}{\hbar}\right ) \times \left [ 1 - \frac{i}{\hbar}\int^{t}_{-\infty} \textrm{exp}\left (\frac{i\hat{H}_{0}t}{\hbar}\right )\hat{H}_{\mu_{e}}\textrm{exp}(\epsilon t_{1})\textrm{exp}\left (-\frac{i\hat{H}t}{\hbar}\right ) \textrm{d}t_{1} \right ]\hspace{1cm} \label{8} \]
Now for the purposes of two-photon absorption we will need to find the 2nd order perturbation. Thus we must find the second iteration of this equation. Where epsilon is a very small number, we come to the following equation for both the first and second order contribution:
\[ \left < \Psi_{f} \left | \hat{H} \right | \Psi_{i} \right > = \frac{1}{\hbar}\frac{\textrm{exp}(-i\omega_{i}t)}{\omega_{i} - \omega_{f}} \left ( \left< \Psi_{f} \left | \hat{H}_{\mu_{e}} \right | \Psi_{i} \right > + \frac{1}{\hbar}\sum_{l}\frac{ \left< \Psi_{f} \left | \hat{H}_{\mu_{e}} \right | \Psi_{l} \right > \left< \Psi_{l} \left | \hat{H}_{\mu_{e}} \right | \Psi_{i} \right >}{\omega_{i} - \omega_{l}} \right )\hspace{1cm} \label{9} \]
Electric Dipole Contribution
The following constants, variables and operators are introduced in this section:
| \(\xi\) | Amplitude of Electric field |
| \(\hat{\mu}\) | Dipole operator = \(e\sum_{i=1}^{N}q_{i}\hat{r}_{i}\) |
For the perturbation method described in the previous section the use of a single iteration accurately describes the transitions between a two levels. This describes the results of Fermi's Golden Rule. However, in order to describe these two-photon processes which transgress through more than one transition, we must look at the second iteration within the perturbation.
\[\hat{H}_{\mu_{e}} = e\hat{\mu}(\hat{E}_{1} + \hat{E}_{2}) \hspace{1cm} \label{10}\]
Where
\[\hat{E_{n}} = \xi_{n}\textrm{cos}(\omega_{n} t)\hspace{1cm} \label{11} \]
Thus
\[\hat{H}_{\mu_{e}} = e\hat{\mu}(\xi_{1}\textrm{cos}(\omega_{1} t) + \xi_{2}\textrm{cos}(\omega_{2} t))\hspace{1cm} \label{12} \]
Substituting this into the second iteration gives us:
\[ \left < \Psi_{f} \left | \hat{H} \right | \Psi_{i} \right > = \]
\[\frac{1}{\hbar}\frac{\textrm{exp}(-i\omega_{i}t)}{\omega_{i} - \omega_{f}} \left ( \left< \Psi_{f} \left |e\hat{\mu}(\hat{E}_{1} + \hat{E}_{2}) \right | \Psi_{i} \right > + \frac{1}{\hbar}\sum_{l}\frac{ \left< \Psi_{f} \left | e\hat{\mu}(\hat{E}_{1} + \hat{E}_{2}) \right | \Psi_{l} \right > \left< \Psi_{l} \left | e\hat{\mu}(\hat{E}_{1} + \hat{E}_{2}) \right | \Psi_{i} \right >}{\omega_{i} - \omega_{l}} \right )\hspace{1cm} \label{13} \]
Looking at this equation we see that the first term is that corresponding to single photon transitions. However, because we are looking for two-photon transitions we can ignore this term and focus on the second term. This second term has a summation to distinguish between the different permutations of arranging the perturbations and achieve the same final state but it includes the interaction of two photons from the same light source which we do not need to consider at the moment. If we eliminate the terms of the sum responsible for these guys we should find the expression for the two permutations of two-photon transitions from our two light sources. Now let us implement these changes.
\[ \left < \Psi_{f} \left | \hat{H} \right | \Psi_{i} \right > = \]
\[ \frac{1}{\hbar^{2}}\frac{\textrm{exp}(-i\omega_{i}t)}{\omega_{i} - \omega_{f}} \left (\frac{ \left< \Psi_{f} \left | e\hat{\mu}\xi_{1}\textrm{cos}(\omega_{1} t) \right | \Psi_{l} \right > \left< \Psi_{l} \left | e\hat{\mu}\xi_{2}\textrm{cos}(\omega_{2} t) \right | \Psi_{i} \right > +\left< \Psi_{f} \left | e\hat{\mu}\xi_{2}\textrm{cos}(\omega_{2} t) \right | \Psi_{l} \right > \left< \Psi_{l} \left | e\hat{\mu}\xi_{1}\textrm{cos}(\omega_{1} t) \right | \Psi_{i} \right >}{\omega_{i} - \omega_{l}} \right ) \hspace{1cm} \label{14} \]
This equation describes the electric dipole contribution towards two-photon transitions.
Selection Rules
The following constants, variables and operators are introduced in this section:
| \(l\) | Angular Momentum Quantum Number |
| \(m_{l}\) | Magnetic Quantum Number |
| \(Y\) | Spherical Harmonic |
|
\(\hat{Z}\) |
Position operator = \(z\) |
| \(\hat{P}_{z}\) | Momentum Operator in the Z direction \(-i\hbar\frac{\textrm{d}}{\textrm{d}z}\) |
In order to take a thorough look at the selection rules for the two-photon system induced by the electric field contribution we must look qualitatively at the results of the equation for the probability of a transition. The Hamiltonian presented in the previous section for the electric dipole contribution is the result of a gauge transformation of the original electric dipole contribution. For the purposes of finding the electric dipole selection rules we shall revert back to the original form.
\[\hat{H}_{\mu_{e}}(t) = \frac{qE}{m\omega}\hat{P}_{z}\textrm{sin }\omega t \hspace{1cm}\label{15} \]
We will consider the effect of the sinusoid part of this equation later in this section. For now let us track the selection rules due only to the operator \(\hat{P}_{z} \).
\[\left [ \hat{Z}, \hat{H}_{0} \right ] = i\hbar\frac{\partial \hat{H}_{0}}{\partial \hat{P}_{z}} = i\hbar\frac{\hat{P}_{z}}{m} \hspace{1cm} \label{16} \]
This can be shown to be true by simply working out the commutator and leads to the following statement
\[\left < \Psi_{f} \left | \left [\hat{Z},\hat{H}_{0} \right ] \right | \Psi_{i} \right > = \left < \Psi_{f} \left | \hat{Z}\hat{H}_{0} -\hat{H}_{0}\hat{Z} \right | \Psi_{i} \right > \hspace{1cm} \label{17} \]
\[ = -(E_{f} - E_{i})\left < \Psi_{f} \left | \hat{Z} \right | \Psi_{i} \right > = \frac{i\hbar}{m}\left < \Psi_{f} \left | \hat{P}_{z} \right | \Psi_{i} \right > \hspace{1cm} \label{18}\]
This shows the result of an electric dipole induced transition for a two level system. However, we need to slightly change things in order to incorporate the three levels that will exist as a result of the two-photon transition as well as the fact that we will have two different perturbations. Thus the Hamiltonian for the two-photon system will be:
\[ \hat{H}_{\mu_{e}}(t) = \frac{qE_{1}}{m\omega_{1}}\hat{P}_{z}\textrm{sin }\omega_{1} t + \frac{qE_{2}}{m\omega_{2}}\hat{P}_{z}\textrm{sin }\omega_{2} t \hspace{1cm}\label{19} \]
Similar to before we can ignore the sinusoid part for later in this section. If we do this we instead come to the result:
\[(E_{f}-E_{l})(E_{l}-E_{i})\left < \Psi_{f} \left | \hat{Z} \right | \Psi_{l} \right > \left < \Psi_{l} \left | \hat{Z} \right | \Psi_{i} \right > \hspace{1cm}\label{20}\]
Whereas the momentum operator is difficult to find the selection rules for, the position operator is fairly straight forward. This is because the variable \(z\), which is the result of the operator \(\hat{Z}\), is equal to the following wavefunction.
\[z = \sqrt{\frac{4\pi}{3}}rY^{0}_{1}(\theta) \hspace{1cm}\label{21} \]
This works under the assumption that the light is polarized in the \(z\) direction but we can also polarize the light in multiple directions as there are two photons. If this is the case we need to expand to define both \(x\) and \(y\) in terms of an angular function. We'll only examine the x case here because it gives the same results.
\[x = \sqrt{\frac{2\pi}{3}}r\left ( Y^{-1}_{1} - Y^{1}_{1} \right ) \hspace{1cm} \label{22} \]
While for our case we have two position operators acting on different kets, however, that has no effect on the ket because multiplication is commutative. This means the angular part of the inner product will result in the integral for the double \(z\) and double \(x\) case respectively. Because all of the results retain the same \(l\) values that will not be addressed until after we first look at the \(m\) values.
\[\int d\Omega Y^{m_{f}\ast}_{l_{f}}(\theta,\phi) Y^{0}_{1}(\theta)Y^{m_{l}}_{l_{l}}(\theta,\phi)Y^{m_{l}\ast}_{l_{l}}(\theta,\phi)Y^{0}_{1}(\theta)Y^{m_{i}}_{l_{i}}(\theta,\phi)\hspace{1cm} \label{23}\]
\[\int d\Omega Y^{m_{f}\ast}_{l_{f}}(\theta,\phi) \left ( Y^{-1}_{1} - Y^{1}_{1} \right )Y^{m_{l}}_{l_{l}}(\theta,\phi)Y^{m_{l}\ast}_{l_{l}}(\theta,\phi)\left ( Y^{-1}_{1} - Y^{1}_{1} \right )Y^{m_{i}}_{l_{i}}(\theta,\phi)\hspace{1cm} \label{24}\]
The intermediate or virtual state angular functions have no effect since they are complex conjugates of each other, their \(l\) and \(m\) values will annihilate each other. Thus the integral we need to be concerned with is:
\[\int d\Omega Y^{m_{f}\ast}_{l_{f}}(\theta,\phi) Y^{0}_{1}(\theta)Y^{0}_{1}(\theta)Y^{m_{i}}_{l_{i}}(\theta,\phi)\hspace{1cm} \label{25})\]
\[\int d\Omega Y^{m_{f}\ast}_{l_{f}}(\theta,\phi) \left ( Y^{-1}_{1} - Y^{1}_{1} \right )\left ( Y^{-1}_{1} - Y^{1}_{1} \right )Y^{m_{i}}_{l_{i}}(\theta,\phi)\hspace{1cm} \label{26}\]
Because the basis to the selection rule is that only a sum of \(m\) values that results in 0 will result in an even function to integrate over, we can now determine a range for \(m\) values. For purely \(Z\) polarized two-photon absorption the sum of the \(m\) values without the initial and final states is still 0, thus the \(\Delta m\) must remain 0. However, for the inclusion of \(Z\) and \(X\) or \(Y\). the sum without the initial and final states will be \(\pm 1 \). Thus in order to retain a total sum of 0 the \(\Delta m\) must be \(\pm 1\). Finally for the pure \(X\), pure \(Y\), and \(XY\) cases the sum from the operators can results in \(\pm 2\) or 0. Therefore, the \(\Delta m=\pm 2, 0 \) to negate the operators.
Now to talk about the \(l\) values. The selection rule that governs them is that we need the sum of all the \(l\) values to be even. Complex conjugate \(l\) values are negative, the same holds true for the \(m\) values. Thus because each operator is has an \(l = 1\) and we now have two operators thus we can have the following possible changes to result in even sums.
\[\Delta l = 0, \pm 2 \]
Now the rationality behind the change in the selection rules will be discussed. Each photon has a unit of momentum with it. During a single photon excitation that momentum must be transferred due to conservation of momentum. Thus if it destructively interferes with the electron it can lower the total momentum by one unit and if it constructively interferes with the electron is can increase the total momentum by one unit. However, for the two photon case, we now have to consider not only the ways in which the photon and electron will interfere but also how the photons will interfere with each other. This results in a doubly constructive interference state with an increase of 2 units, one constructive and one destructive interference state that results in no change and a doubly destructive interference state that results in a decrease of 2 units.
Inversion Selection Rules
If we take a look at the equation presented at the end of the electric dipole section, it is a simple analysis to derive the basic selection rules for electric dipole induced two-photon transitions. However, we do not need to consider the constant values to determine selection rules as they only determine the intensity of the signal, not the existence of the peak. Where C is a constant:
\[ \left < \Psi_{f} \left | \hat{H} \right | \Psi_{i} \right > = \]
\[C \left ( \left< \Psi_{f} \left | e\hat{\mu}\xi_{1}\textrm{cos}(\omega_{1} t) \right | \Psi_{l} \right > \left< \Psi_{l} \left | e\hat{\mu}\xi_{2}\textrm{cos}(\omega_{2} t) \right | \Psi_{i} \right > +\left< \Psi_{f} \left | e\hat{\mu}\xi_{2}\textrm{cos}(\omega_{2} t) \right | \Psi_{l} \right > \left< \Psi_{l} \left | e\hat{\mu}\xi_{1}\textrm{cos}(\omega_{1} t) \right | \Psi_{i} \right > \right ) \hspace{1cm} \label{27} \]
Although for one-photon transitions the dipole moment is of considerable importance. We notice that because both terms contain two dipole moments, regardless of whether they are odd or even, their combination will still become even. Furthermore, we can see that because the wave part of the electric field is an even function, that this too will preserve parity of the transition in both terms, even if it were an odd function as each term contains two of such functions. Thus the result is that as long as the final and initial state conserve parity (inversion symmetry or antisymmetry is maintained) the transition will be allowed. This is different from one-photon processes where parity conservation is forbidden and makes two-photon spectroscopy especially useful.
Magnetic Dipole Contribution
The following constants, variables, and operators are introduced in this section:
| \(\hat{L_{x}}\) | Angular momentum Operator \(i\hbar\left (\textrm{sin }\phi\frac{\partial}{\partial\theta} + \textrm{cot }\theta\textrm{cos }\phi\frac{\partial}{\partial \phi}\right ) \) |
| \(\hat{S}_{x}\) | Spin momentum Operator \(\frac{\hbar}{2}\sigma_{x}\) |
| \(\sigma_{x}\) | Pauli Matrix |
| B | Strength of Magnetic Field |
The magnetic dipole contribution is determined by the Magnetic dipole Hamiltonian:
\[\hat{H}_{DM} = -\frac{q}{2m}(\hat{L_{x}} + 2\hat{S_{x}})B\textrm{cos}(\omega t) \hspace{1cm} \label{28} \]
where B is the strength of the magnetic field. So for the two photon case we have:
\[\hat{H}_{DM} = -\frac{q}{2m}\left [(\hat{L_{x}} + 2\hat{S_{x}})B_{1}\textrm{cos}(\omega_{1} t) +(\hat{L_{x}} + 2\hat{S_{x}})B_{2}\textrm{cos}(\omega_{2} t)\right ]\hspace{1cm} \label{29}\]
Be aware that the photons do not need to be from the same polarization as they are here. One could be polarized in the X direction while the other is polarized in the Z direction. We will cover these situations in the derivation of the selection rules.
If we similarly substitute this Hamiltonian into the second iteration for perturbation we get:
\[ \left < \Psi_{f} \left | \hat{H} \right | \Psi_{i} \right > = \frac{1}{\hbar}\frac{\textrm{exp}(-i\omega_{i}t)}{\omega_{i} - \omega_{f}} \Bigg( \left< \Psi_{f} \left |-\frac{q}{2m}(\hat{L_{x}} + 2\hat{S_{x}})\left [B_{1}\textrm{cos}(\omega_{1} t) +B_{2}\textrm{cos}(\omega_{2} t)\right ] \right | \Psi_{i} \right > + \]
\[\small{\sum_{l}\frac{ \left< \Psi_{f} \left |-\frac{q}{2m}(\hat{L}_{x} + 2\hat{S}_{x})\left [B_{1}\textrm{cos}(\omega_{1} t) +B_{2}\textrm{cos}(\omega_{2} t)\right ] \right | \Psi_{l} \right> \left<\Psi_{l} \left |-\frac{q}{2m}(\hat{L}_{x} + 2\hat{S}_{x})\left [B_{1}\textrm{cos}(\omega_{1} t) +B_{2}\textrm{cos}(\omega_{2} t)\right ] \right | \Psi_{i} \right >}{\hbar(\omega_{i} - \omega_{l})} \Bigg)} \hspace{1cm}\label{30}\]
We can ignore the first term of this equation as it corresponds to the magnetic dipole contribution of the single photon transitions. From the summation we can ignore the squared terms as well because they represent the two photon transitions due to the beam interfering with itself. While that does exist and may be relevant for some spectroscopic work, here we are looking at the two-photon absorption from two light sources.
\[ \left < \Psi_{f} \left | \hat{H} \right | \Psi_{i} \right > = \]
\[ \small{\frac{q^{2}\textrm{cos }(\omega_{1}t)\textrm{cos }(\omega_{2} t)}{4m^{2}\hbar^{2}}\frac{\textrm{exp}(-i\omega_{i}t)}{\omega_{i} - \omega_{f}} \left ( \frac{ \left< \Psi_{f} \left | (\hat{L}_{x} +2\hat{S}_{x}) \right | \Psi_{l} \right > \left< \Psi_{l} \left | (\hat{L}_{x} +2\hat{S}_{x}) \right | \Psi_{i} \right > +\left< \Psi_{f} \left | (\hat{L}_{x} +2\hat{S}_{x}) \right | \Psi_{l} \right > \left< \Psi_{l} \left | (\hat{L}_{x} +2\hat{S}_{x}) \right | \Psi_{i} \right >}{\omega_{i} - \omega_{l}} \right )} \hspace{1cm} \label{31}\]
Selection Rules
Just as before, our selection rules stem from the magnetic dipole Hamiltonian:
\[\hat{H}_{DM} = -\frac{q}{2m}(\hat{L_{x}} + 2\hat{S_{x}})B\textrm{cos}(\omega t) \hspace{1cm} \label{32} \]
Here, as before, the sinusoid part is even and thus will have no effect on the selection rules. We must look at the operators to determine the selection rules.
Because neither \(\hat{L}_{x}\) or \(\hat{S}_{x}\) have any effect on the value of \(l\) the selection rule for \(\Delta l\) is 0. However both \(\hat{L}_{x}\) and \(\hat{S}_{x}\) can change their corresponding \(m_{l}\) and \(m_{s}\) values by one unit. For \(m_{s}\) this corresponds to changing the spin of the electron. If the magnetic field is perpendicular to the spin of the system, then the \(\Delta m_{s}\) can also have a value of 0. If we extrapolate this to a two photon system then the same \(m_{s}\) values should still apply given that even if it is changed by 1 by the first photon, it can change back by -1 or remain in the \(+\frac{1}{2}\) state as those are the only two options. Therefore, we should expect the same selection rules for \(\Delta m_{s} = 0, \pm1\) in a two-photon system.
Modern Research Interests
Two-photon absorption has traditionally been a large part of the spectroscopy field. However, it was only within the past decade that biomedical applications have returned it to the spotlight. Two-photon absorption, and potentially all nonlinear absorptions, allow for unprecedented depth in medical imaging technology. Traditional single photon methods result in an enormous amount of scattering from the biological tissue samples. However, these nonlinear optics allow for the assignment of the scattered photons to their origins.
Much of the research in this area is focused on maximizing the depth and clarity of the signal for this potentially non-intrusive medical procedure. Several parameters have been looked at including excitation wavelength, beam size, pulse width, and pulse frequency. As of now the largest depths achievable are around 1 mm.
References
- Cohen-Tannoudji, Claude & Diu, Bernard & Laloe, Franck; 2005; Quantum Mechanics; Paris, France; Hermann
- Eberly, Joseph & Lambropoulos, Peter; 1977; Multiphoton Processes; Rochester, New York; John Wiley & Sons
- Garrett, C. G. B., Laboratories, B. T., & Hill, M. 1961. Two-Photon Excitation in CaF\(_{2}\)Eu\(^{2+}\), 7(6), 229–232.
- Helmchen and Denk, “Deep Tissue Two-photon Microscopy.”, Nature Methods, 2005, 2, 932-940
- Loudon, Rodney; (1983); The quantum theory of light; New York; Oxford Publishing
- Masters, Barry R.; English translation of: Göppert, M. (1929). Über die Wahrscheinlichkeit des Zusammenwirkens zweier Lichtquanten in einem Elementarakt. (2010)., 1929, 273–294.
- Tsukerblat, Boris; Group Theory in Chemistry and Spectroscopy: A Simple Guide to Advanced Usage; 2006; Mineola, New York; Dover Publications
Problems
- Derive the expression for the quadrupole contribution to the probability of a two-photon transition.
- Find the third iteration of the Hamiltonian from the Perturbation adjustment using the iterative equation.
- Use this third iteration to find the quantum mechanical selection rules for the electric dipole contribution to a three-photon process.

