Dipole moments
- Page ID
- 1659
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The intermolecular forces have important contribution in helping us to understand the interaction between atoms in same or different kind of molecules. The interaction can involve polar or non polar molecules and ions. There are three common intermolecular forces and this module will focus more in-depth the interaction involving polar molecules and interaction between polar molecules and ions.
Introduction
Dipole moment (\(\mu\)) is the measure of net molecular polarity, which is the magnitude of the charge \(Q\) at either end of the molecular dipole times the distance \(r\) between the charges.
\[\mu = Q \times r\]
Dipole moments tell us about the charge separation in a molecule. The larger the difference in electronegativities of bonded atoms, the larger the dipole moment. For example, NaCl has the highest dipole moment because it has an ionic bond (i.e. highest charge separation).
In the Chloromethane molecule (CH3Cl), chlorine is more electronegative than carbon, thus attracting the electrons in the C—Cl bond toward itself (Figure 1). As a result, chlorine is slightly negative and carbon is slightly positive in C—Cl bond. Since one end of C-Cl is positive and the other end is negative, it is described as a polar bond. To indicate the increased in electron density, the dipole is represented by an arrow with a cross at one end. The cross end of the arrow represents the positive end and the point of the arrow represents the negative end of the dipole.
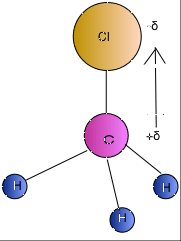
The vector will point from plus to minus charge and run parallel with the bond between 2 atoms. The symbol δ indicates the partial charge of an individual atom. In addition, the direction of vector implies the physical movement of electrons to an atom that has more electronegativity when 2 atoms are separated by a distance of r. In other words, the electrons will spend more time around atom that has larger electronegativity.
| Compound | Dipole Moment (Debyes) |
|---|---|
| NaCl | 9.0 (measured in the gas phase) |
| CH3Cl | 1.87 |
| H2O | 1.85 |
| NH3 | 1.47 |
| CO2 | 0 |
| CCl4 | 0 |
Polar molecules and Dipole-Dipole Interaction
A polar molecule is a molecule where one end has a positive electrical charge and the other end has a negative charge due to the arrangement or geometry of its atoms. Because polar molecules have a positive and negative charge ends, the positive charge end of a molecule will attract to the negative end of adjacent molecule with the same or different kind of molecule. The attraction beween two polar molecules is called dipole-dipole interaction. The attraction between two dipoles create a very strong intermolecular force, which have great influence in the evaporation of liquid and condensation of gas.
Since water are polar molecules, the interaction between water molecules are so strong that it takes a lot of energy to break the bond between the water molecules. Therefore, the boiling point of polar substances are higher than those of nonpolar substance due to stronger intermolecular force among polar molecules.
Polar molecules and Ions Interaction
When a polar molecule is mixed with ion, the positive charge end of the polar molecule will be attracted to the negative charge called anion on the ion. Also, the positive charge called cation on the ion will be attracted to the negative charge end of the polar molecule. This ion-dipole interaction is stronger than the dipole-dipole interaction between polar molecules, but is weaker than the ion-ion interaction.
Since ions and polar molecule have positive and negative charge, we can use Coulomb's law to evaluate the force between them
\[ F = k_e \dfrac{q_1q_2}{r^2}\]
with
- \(q_1\) and \(q_2\) are the charges on atoms
- \(k_e\) is the proportionality constant
- \(r_{12}\) is the distance between 2 separated charges
The strength of ion-dipole interaction is based on the distance between ion and polar molecule, the charge of the ion, and dipole magnitude. The closer ion and polar molecule are, the stronger the intermolecular force is between polar molecule and ion. An ion with higher charge will make the attraction stronger. Last, a greater magnitude of dipole will cause stronger attraction.
References
- Fay, McMurry. Chemistry Fourth Edition, Pearson Education, New Jersey, 2004
- Kotz, Treichel, Weaver. Chemistry and Chemical Reactivity, Thomson Brooks/Cole, 2006

