Overview of Intermolecular Forces
- Page ID
- 1507
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Intermolecular forces are forces between molecules. Depending on its strength, intermolecular forces cause the forming of three physical states: solid, liquid and gas. The physical properties of melting point, boiling point, vapor pressure, evaporation, viscosity, surface tension, and solubility are related to the strength of attractive forces between molecules. These attractive forces are called Intermolecular Forces. The amplitude of interaction is important in the interpretation of the various properties listed above.
Introduction
There are four types of intermolecular forces. Most of the intermolecular forces are identical to bonding between atoms in a single molecule. Intermolecular forces just extend the thinking to forces between molecules and follows the patterns already set by the bonding within molecules.
Coulombic Forces
The forces holding ions together in ionic solids are electrostatic forces. Opposite charges attract each other. These are the strongest intermolecular forces. Ionic forces hold many ions in a crystal lattice structure. According to Coulomb’s law:
\[ V=-\dfrac{q_1 q_2}{4 \pi \epsilon r} \tag{1}\]
- \(q\) is the charges.
- \(r\) is the distance of separation.
Based on Coulomb’s law, we can find the potential energy between different types of molecules.
Dipole Forces
Polar covalent molecules are sometimes described as "dipoles", meaning that the molecule has two "poles". One end (pole) of the molecule has a partial positive charge while the other end has a partial negative charge. The molecules will orientate themselves so that the opposite charges attract principle operates effectively.
In the figure below, hydrochloric acid is a polar molecule with the partial positive charge on the hydrogen and the partial negative charge on the chlorine. A network of partial + and - charges attract molecules to each other.

\[ V=-\dfrac{3}{2}\dfrac{I_A I_B}{I_A+I_B}\dfrac{\alpha_A \alpha_B}{r^6} \tag{3}\]
Dipole-Dipole Interactions
When a polar molecule encounters another polar molecule, the positive end of one molecule is attracted to the negative end of the other polar molecule. Many molecules have dipoles, and their interaction occur by dipole-dipole interaction. For example: SO2 ↔SO2. (approximate energy: 15 kJ/mol). Polar molecules have permanent dipole moments, so in this case, we consider the electrostatic interaction between the two dipoles:
\[ V=-\dfrac{2}{3}\dfrac{\mu_1^2 \mu_2^2}{(4\pi\epsilon_0)^2 r^6} \tag{4}\]
µ is the permanent dipole moment of the molecule 1 and 2.
Ion-Dipole Interactions
Ion-Dipole interaction is the interaction between an ion and polar molecules. For example, the sodium ion/water cluster interaction is approximately 50 KJ/mol.
\[ Na^+ ↔ (OH_2)_n \tag{5}\]
Because the interaction involves in the charge of the ion and the dipole moment of the polar molecules, we can calculate the potential energy of interaction between them using the following formula:
\[ V=-\dfrac{q\mu}{(4\pi\epsilon_0) r^2} \tag{6}\]
- r is the distance of separation.
- q is the charge of the ion ( only the magnitude of the charge is shown here.)
- \(\mu\) is the permanent dipole moment of the polar molecule.
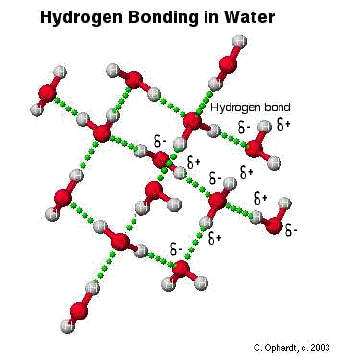
Hydrogen Bonding
The hydrogen bond is really a special case of dipole forces. A hydrogen bond is the attractive force between the hydrogen attached to an electronegative atom of one molecule and an electronegative atom of a different molecule. Usually the electronegative atom is oxygen, nitrogen, or fluorine. In other words - The hydrogen on one molecule attached to O or N that is attracted to an O or N of a different molecule.
In the graphic below, the hydrogen is partially positive and attracted to the partially negative charge on the oxygen or nitrogen. Because oxygen has two lone pairs, two different hydrogen bonds can be made to each oxygen. This is a very specific bond as indicated. Some combinations that are not hydrogen bonds include: hydrogen to another hydrogen or hydrogen to a carbon.
Induced Dipole Forces
Forces between essentially non-polar molecules are the weakest of all intermolecular forces. "Temporary dipoles" are formed by the shifting of electron clouds within molecules. These temporary dipoles attract or repel the electron clouds of nearby non-polar molecules.
The temporary dipoles may exist for only a fraction of a second but a force of attraction also exist for that fraction of time. The strength of induced dipole forces depends on how easily electron clouds can be distorted. Large atoms or molecules with many electrons far removed from the nucleus are more easily distorted. Review - Non-Polar Bonds

London Dispersion force
London Dispersion Force, also called induced dipole-induced dipole, is the weakest intermolecular force. It is the interaction between two nonpolar molecules. For example: interaction between methyl and methyl group: (-CH3 ↔ CH3-). (approximate energy: 5 KJ/mol)
When two non polar molecules approach each other, attractive and repulsive forces between their electrons and nuclei will lead to distortions in these electron clouds, which mean they are induced by the neighboring molecules, and this leads to the interaction. We can calculate the potential energy between the two identical nonpolar molecule as followed formula:
\[ V=-\dfrac{3}{4} \dfrac{\alpha^2 I}{r^6} \tag{2}\]
- α is the polarizability of nonpolar molecule.
- r is the distance between the two molecule.
- I = the first ionization energy of the molecule.
Negative sign indicates the attractive interaction. For two nonidentical nonpolar molecules A and B, we have the formula:
Problems
- Two HBr molecules (u= 0.78 D) are separate by 300pm in air. Calculate the dipole-dipole interaction energy in KJ/mol if they are oriented from end to end.
- Calculate the potential energy of interaction of a sodium ion that is at 3 Amstrong from HCl molecule with a dipole moment of 1.08 D.
- Calculate the potential energy of interaction between two He atoms separated by 5 Amstrong in the air. (polarizability = 0.20x 10-30 m3 . I = 2373 KJ/mol)
Solution
- 1D=3.3356x10-30Cm; 300pm=3 Amstrong= 3x10-10m. V=-2.7 KJ/mol
- -35 KJ/mol
- -0.0045 KJ/mol
References
- Kotz, Treichel, Weaver. Chemistry and Chemical reactivity, sixth ed. Thompson, 2006.
- Donald Allan McQuarrie, John Douglas Simon. Physical Chemistry: a molecular approach. University Science Books, 1997.

