19: Electrochemistry

These are homework exercises to accompany the Textmap created for "General Chemistry: Principles and Modern Applications " by Petrucci et al. Complementary General Chemistry question banks can be found for other Textmaps and can be accessed here. In addition to these publicly available questions, access to private problems bank for use in exams and homework is available to faculty only on an individual basis; please contact Delmar Larsen for an account with access permission.

Chemical reactions can be used to produce electricity. This electricity can be used in several different ways, and is applied in a variety of methods in our everyday lives. In studying theoretical cells and reactions, we can get a better understanding of the flow of electrons. The following practice problems are to assist in your mastery of the topic of Electrochemistry.

Q19.1A

From the following observations, estimate the \(\mathrm{E^\circ}\) from the half reaction \(\mathrm{M^+(aq) + e^- \rightarrow M(s)}\):

1. The metal \(\ce{M}\) reacts with \(\ce{H2SO4(aq)}\); but not with \(\ce{HI(aq)}\); \(\ce{M}\) displaces \(\ce{Au+(aq)}\), but not \(\ce{Fe^3+(aq)}\).
2. The metal \(\ce{M}\) reacts with \(\ce{HI(aq)}\), producing \(\ce{H2(g)}\), but displaces neither \(\ce{Al^3+(aq)}\) nor \(\ce{Na+(aq)}\).

S19.1A

1. If the metal dissolves in \(\ce{H2SO4}\), it has a reduction potential that is smaller than \(\mathrm{E^\circ_{SO_4^{2-} (aq) / SO_2 (g)} = 0.17\:V}\). If it does not dissolve in \(\ce{HI}\), it has a reduction potential that is larger than \(\mathrm{E^\circ_{H^+ (aq) / H_2 (g)} = 0\:V}\). If it displaces \(\ce{Au+(aq)}\) from solution, then it has a reduction potential smaller than \(\mathrm{E^\circ_{Au^+ (aq) / Au (s)} = 1.68\:V}\). But if it does not displace \(\ce{Fe^3+(aq)}\) from solution, then its reduction potential is larger than

\(\mathrm{E^\circ_{Fe^{3+}(aq) / Fe^{2+}(s)} = 0.769\: V}\).

Therefore, \(\mathrm{0\:V < E^\circ < 0.17\: V}\).

2. If the metal dissolves in \(\ce{HI (aq)}\), it has a reduction potential that is smaller than \(\mathrm{E^\circ_{H^+(aq)/H_2(g)}=0\:V}\). If it does not displace \(\ce{Al^3+ (aq)}\) from solution, its reduction potential is larger than \(\mathrm{E^\circ_{Al^{3+} (aq) / Al (s)}= -1.676\:V}\). If it also does not displace \(\ce{Na+ (aq)}\) from solution, its reduction potential is larger than \(\mathrm{E^\circ_{Na^+(aq)/Na(s)} = -2.7144\:V}\). Therefore, \(\mathrm{-1.7676\: V < E^\circ < 0\: V}\).

Q19.1B

Estimate the \(\mathrm{E^\circ}\) for half reaction \(\mathrm{M^{2+}(aq)+2e^- \rightarrow M(s)}\)_. Metal \(\ce{M}\) reacts with \(\ce{HF(aq)}\), but not with \(\ce{HCl (aq)}\); \(\ce{M}\) displaces \(\ce{Fe^3+(aq)}\), but not \(\ce{Sn^4+(aq)}\).

S19.1B

\(\mathrm{+0.13\:V < E^{\circ} < +0.77\:V}\)

When \(\ce{M}\) react (including displace) with any substance, its \(\mathrm{E^\circ}\) is less than that substance's \(\mathrm{E^\circ}\) and when it doesn't react, its \(\mathrm{E^\circ}\) is more than that substance's. Thus the answer is: \(\mathrm{+0.13\:V < E^{\circ} < +0.77\:V}\).

Q19.1C

For the half reaction, \(\mathrm{M^{2+}(aq) +2e^- \rightarrow M(s)}\), what range of \(\mathrm{E_0}\) is possible if:

\(\ce{M}\) displaces \(\ce{MnO4- (aq)}\), but not \(\ce{AgCl(s)}\). \(\ce{M}\) is unable to react with \(\ce{HCl}\), but reacts with \(\ce{HNO3}\).

S19.1C

Since the reaction can displace \(\ce{MnO4- (aq)}\), it would be able to have a standard reaction up to +0.56. However, since it cannot displace \(\ce{AgCl(s)}\), its standard reaction potential would be above +0.2223.

Therefore:
\(\mathrm{+0.2223\: V < E_0 < +0.560\: V}\)

Q19.1D

From the observation listed, estimate the value of \(\mathrm{E^\circ}\) for the half reaction.
\(\mathrm{M^{2+} (aq) + 2e^{2-} \rightarrow M(s)}\)

1. The metal \(\ce{M}\) reacts with \(\ce{HNO3}\), and \(\ce{M}\) can replace \(\ce{Ag+}\) but not \(\ce{Cu^2+}\).
2. The metal reacts with \(\ce{HNO3}\) and it can not produce \(\ce{H2}\); however, it can interact with \(\ce{Fe}\).

S19.1D

1. \(\mathrm{0.223 < x < 0.340}\)
2. \(\mathrm{-0.440<x< 0}\)

Q19.1E

Using the table of Standard Reduction Potential and the following clues, determine the metal \(\ce{M}\).

1. \(\ce{M}\) will be oxidized by \(\ce{F2(g)}\), but will be reduced by \(\ce{Fe^2+(aq)}\)
2. \(\ce{M}\) will reduce \(\ce{Br2(l)}\), but will oxidize \(\ce{I2(s)}\)

S19.1E

1. Because \(\ce{M}\) will be oxidized by \(\ce{F2(g)}\) and reduced by \(\ce{Fe^3+(aq)}\) the reduction potential will be between 2.866 and 0.771.
2. Because \(\ce{M}\) will reduce \(\ce{Br2(l)}\), the reduction potential of \(\ce{M}\) must be less then 1.065. \(\ce{M}\) will have a reduction potential of 1.065 to 0.077.

Q19.1F

From the observations listed, estimate the value of \(\mathrm{E^\circ}\) for the imaginary half reaction \(\mathrm{M^{2+} + 2e^- \rightarrow M(s)}\), where \(\mathrm{M}\) is an unknown metal to be determined under the following conditions:

1. The metal \(\mathrm{M}\) reacts with \(\ce{HCl (aq)}\).
2. The metal displaces \(\ce{Fe^3+}\) but does not displace \(\ce{Sn^4+}\).
3. The metal reacts with \(\ce{HNO3 (aq)}\).
4. The metal can displace \(\ce{K+ (aq)}\).

S19.1F

1. The \(\mathrm{E^\circ}\) value will be estimated to be less than 0. In Table P2, metals listed below hydrogen (\(\ce{Pb}\) through \(\ce{Li}\)) should react with \(\ce{HCl}\). Metals with an \(\mathrm{E^\circ}\) above hydrogen will not. These metals must be able to displace \(\ce{H2(g)}\) from acidic solutions.
2. The \(\mathrm{E^\circ}\) value will be between +0.771 and +0.154. Being displaced means that the ion is forced out of solution and into metal state. The metal must be above \(\ce{Sn^4+}\) indicating it is a stronger reducing agent (more willing to give up electrons) and below \(\ce{Fe^3+}\).
3. The \(\mathrm{E^\circ}\) value must be lower than 0.956, the \(\mathrm{E^\circ}\) for \(\ce{NO3}\)_. This follows the same reasoning in 1a, but this time the metal must be able to displace \(\ce{NO (g)}\) from acidic solution. Thus, the predicted \(\mathrm{E^\circ}\) value will be lower than 0.956.
4. The \(\mathrm{E^\circ}\) must be lower than -2.924, meaning that the metal \(\ce{M}\) will get oxidized and will push the \(\ce{K+}\) ion into solution. Thus, the \(\mathrm{E^\circ}\) will be lower than -2.924.

For review on this topic, visit the page "Electrochemistry 1: Introduction".

Q19.2A

A Lithium-ion battery has a theoretical \(\mathrm{E_0}\) cell of 1.5 V. Find the \(\mathrm{E_0}\) for the reduction half-reaction:

\(\mathrm{Li^+(aq) + e^- \rightarrow Li(s)}\)

S19.2A

The \(\mathrm{E^\circ}\) for the reaction \(\mathrm{Li^+ (aq) + e^- \rightarrow Li(s)}\) equals -3.040 according to the Standard Electrode Potential Table.

Q19.2B

Use the table of Standard Reduction Potential to predict whether these reactions will happen spontaneously.

1. \(\mathrm{2Ag^+(aq) + Cu(s) \rightarrow 2Ag(s) + Cu^{2+}(aq)}\)
2. \(\mathrm{Fe^{3+}(aq) + Na(s) \rightarrow Fe^{2+}(aq) + Na^+(aq)}\)
3. \(\mathrm{Zn^{2+}(aq) + 2I^-(aq) \rightarrow Zn(s) + I_2(l)}\)

S19.2B

1. The reduction potential of \(\ce{Ag+(aq)}\) is 0.8
   The oxidation potential of \(\ce{Cu(s)}\) is -0.34
   \(\mathrm{E^\circ_{cell} = E^\circ_{Cat} + E^\circ_{An}}\): \(\mathrm{0.8 + (-0.34) = 0.46}\)
   \(\mathrm{E^\circ_{cell}}\) is positive, Yes it will happen spontaneously
2. The reduction potential of \(\ce{Fe^3+(aq)}\) is 0.77
   The oxidation potential of \(\ce{Na(s)}\) is 2.71
   \(\mathrm{E^\circ_{cell} = E^\circ_{Cat} + E^\circ_{An}}\): \(\mathrm{0.77 + 2.71 = 3.48}\)
   \(\mathrm{E^\circ_{cell}}\) is positive, Yes it will happen spontaneously
3. The reduction potential of \(\ce{Zn^2+(aq)}\) is -0.763
   The oxidation potential of is -0.54
   \(\mathrm{E^\circ_{cell} = E^\circ_{Cat} + E^\circ_{An}}\): \(\mathrm{(-0.763) + (-0.54) = -1.303}\)
   \(\mathrm{E^\circ_{cell}}\) is Negative, No it will not happen spontaneously

Q19.3A

Write the voltaic cell for the reaction between \(\ce{I2(s)}\) and \(\ce{Sn^4+(aq)}\). Determine which half reaction is the cathode and the anode and calculate the reaction standard potential.

Assuming all the reactants and products are in their standard state, use Table P2 to predict which reactions are spontaneous (in the forward direction).

1. \(\mathrm{Zn^{2+} + Cu(s) \rightarrow Cu^{2+}+ Zn(s)}\)
2. \(\mathrm{Fe^{3+} (aq) + Cu(s) \rightarrow Fe^{2+}+ Cu^{2+}(aq)}\)
3. \(\mathrm{2Fe^{2+}(aq) + Cl_2(g) \rightarrow 2Fe^{3+}(aq) +2Cl^-(aq)}\)
4. \(\mathrm{Cu^{2+} + e^- \rightarrow Cu^{2+}}\)

S19.3A

1. Half reaction:

Reduction: \(\mathrm{Zn^{2+} + Cu(s)\rightarrow Cu^{2+} + Zn(s) \quad E^\circ= -0.763\,V}\)

Oxidation: \(\mathrm{Cu(s) \rightarrow Cu^{2+} +2e^- \quad E^\circ=-0.340\,V}\)

\(\begin{align}
\mathrm{E^\circ_{cell}} & = \mathrm{E_{cathode} - E_{anode}} \\
& = -0.763 - 0.340 \\
& = -1.103\,\mathrm{V\, (Spontaneous)}
\end{align}\)

2. Half reaction:

Reduction: \(\mathrm{Fe^{3+} + e^- \rightarrow Fe^{2+} \quad E=0.771\,V}\)

Oxidation: \(\mCathrm{Cu(s) \rightarrow Cu^{2+} + 2e^- \quad E= 0.340\,V}\)

\(\begin{align}
\mathrm{E^\circ_{cell}} & = \mathrm{E_{cathode} - E_{anode}} \\
& = 0.771- 0.340 \\
& = 0.431\,\mathrm{V\, (N.S)}
\end{align}\)

3. Half reaction:

Reduction: \(\mathrm{Cl_2(g) + 2e^- \rightarrow 2Cl^- \quad E= +1.358\,V}\)

Oxidation: \(\mathrm{2Fe^{2+} \rightarrow 2Fe^{3+} + 2e^-}\)

\(\begin{align}
\mathrm{E^\circ_{cell}} & = \mathrm{E_{cathode} - E_{anode}} \\
& = 1.358-0.771\,\mathrm V \\
& = 0.587\,\mathrm{V\, (N.S)}
\end{align}\)

4. It’s already half reaction

Reduction: \(\mathrm{Cu^{2+} + e^- \rightarrow Cu^+ \quad E= +0.159\,V\, (N.S)}\)

S19.3B

\(\mathrm{I_2(s) + 2e^- \rightarrow 2I^-(aq)}\)
\(\mathrm{Sn^{4+}(aq) + 2e^- \rightarrow Sn^{2+}(aq)}\)

\(\mathrm{E^\circ: +0.535\,V\:Reduction \Rightarrow Cathode}\)
\(\mathrm{E^\circ: +0.154\,V\: Oxidation \Rightarrow Anode}\)

\(\mathrm{\Rightarrow Pt(s)|Sn^{2+}(aq),\,Sn^{4+}(aq)|| I_2(s)| 2I^- (aq)}\)

Note: \(\ce{Pt(s)}\) serves as an electrode conductor and does not affect the overall reaction. Since both the \(\ce{Sn}\) reactant and product are both aqueous solutions, \(\ce{Pt}\) or other metal conductors can be used in place.

\(\mathrm{E^\circ = E^\circ_{(cathode)} - E^\circ_{(anode)}}\)
\(\mathrm{E^\circ= (+0.535\,V)-( +0.154\,V)}\)
\(\mathrm{E^\circ= +0.0381\,V}\)

Q19.3B

Write cell reactions for the electrochemical cells diagrammed here, and use data from Table P2 to calculate \(\mathrm{E^\circ_{cell}}\) for each reaction.

1. \(\mathrm{Al(s)| Al^{3+}|| Zn^{2+}(aq)| Zn(s)}\)
2. \(\mathrm{Pt (s)| Fe^{2+}(aq), Fe^{3+}(aq)|| Cu^{2+}(aq)| Cu(s)}\)
3. \(\mathrm{Pt (s)| Cr_2O_7, Cr^{3+}(aq)|| Ag^+(aq)| Ag(s)}\)
4. \(\mathrm{O_2^-(aq)| O_2(g)|| H^+(aq)|H_2(g)| C(s)}\)

S19.3B

1. Half reaction:

Reduction: \(\mathrm{Al(s) + 3e^- \rightarrow Al^{3+} \quad E=-2.310\,V}\)

Oxidation: \(\mathrm{Zn^{2+} \rightarrow Zn(s) + 2e^- \quad E=-0.763\,V}\)

\(\begin{align}
\mathrm{E} & = \mathrm{E_{cathode} - E_{anode}} \\
& = -2.310- -0.763\,\mathrm V \\
& = 1.447\,\mathrm{V}
\end{align}\)

2. Oxidation: \(\mathrm{Fe^{3+} + e^- \rightarrow Fe^{2+} \quad E=0.771\,V}\)

Reduction: \(\mathrm{Cu(s)\rightarrow Cu^{2+} + 2e^- \quad E= 0.520\,V}\)

\(\begin{align}
\mathrm{E} & = \mathrm{E_{cathode} - E_{anode}} \\
& = 0.520- 0.771\,\mathrm V \\
& = 0.149\,\mathrm{V}
\end{align}\)

3. \(\mathrm{Cr^{6+} + 3e^- \rightarrow Cr^{3+} \quad E=1.33\,V}\)

\(\mathrm{Ag(s) \rightarrow Ag^+ + e^- \quad E=0.800\,V}\)

\(\begin{align}
\mathrm{E} & = \mathrm{E_{cathode} - E_{anode}} \\
& = \mathrm{0.800\,V-1.33\,V} \\
& = -0.53\,\mathrm{V}
\end{align}\)

4. \(\mathrm{O_2 + 4H^+ + 4e^- \rightarrow 2H_2O(l) \quad E = 1.229\,V}\)

\(\mathrm{H_2 \rightarrow 2H^+ + e^- \quad E=0\,V}\)

\(\begin{align}
\mathrm{E} & = \mathrm{E_{cathode} - E_{anode}} \\
& = 0- 1.229\,\mathrm V \\
& = -1.229\,\mathrm{V}
\end{align}\)

Q19.3C

For the electrochemical cells shown below, write the cell reactions and find \(\mathrm{E^\circ_{cell}}\) using the Standard Reduction Potential table

1. \(\mathrm{Cu(s) | Cu^{2+}(aq) || Ag^+(aq) | Ag(s)}\)
2. \(\mathrm{Cu(s) | Cu^{2+}(aq) || Fe^{2+}(aq),\,Fe^{3+}(aq) | Pt(s)}\)
3. \(\mathrm{PbO_2(s) | Pb^{2+}(aq) || Mn^{2+}(aq) | MnO_2(s)}\)
4. \(\mathrm{Cu(s) | Cu^{2+}(aq) || O_2(g) | H_2O_2(aq) | Pt(s)}\)

S19.3C

1. \(\ce{2Ag+(aq) + Cu(s) \rightarrow 2Ag(s) + Cu^2+(aq)}\)
   The reduction potential of \(\ce{Ag+(aq)}\) is 0.8
   The oxidation potential of \(\ce{Cu(s)}\) is -0.34
   \(\mathrm{E^\circ_{cell} = E^\circ_{Cat} + E^\circ_{An}}\): \(\mathrm{0.8 + (-0.34) = 0.46}\)
2. \(\ce{2Fe^3+(aq) + Cu(s) \rightarrow 2Fe^2+(aq) + Cu^2+(aq)}\)
   The reduction potential of \(\ce{2Fe^3+(aq)}\) is 0.77
   The oxidation potential of \(\ce{Cu(s)}\) is -0.34
   \(\mathrm{E^\circ_{cell} = E^\circ_{Cat} + E^\circ_{An}}\): \(\mathrm{0.77 + (-0.34) = 0.43}\)
3. \(\ce{PbO2(s) + Mn^2+(aq) \rightarrow Pb^2+(aq) + MnO2(s)}\)
   The reduction potental of \(\ce{PbO2(s)}\) is 1.455
   The oxidation potental of \(\ce{Mn^2+(aq)}\) is -1.229
   \(\mathrm{E^\circ_{cell} = E^\circ_{Cat} + E^\circ_{An}}\): \(\mathrm{1.455 + (-1.229) = 0.43}\)
4. \(\ce{Cu(s) + O2(g) + 2H3O(aq) \rightarrow H2O2(aq) + Cu^2+(aq)}\)
   The reduction potential of \(\ce{O2(g)}\) is 0.695
   The oxidation potential of \(\ce{Cu(s)}\) is -0.34
   \(\mathrm{E^\circ_{cell} = E^\circ_{Cat} + E^\circ_{An}}\): \(\mathrm{0.695 + (-0.34) = 0.355}\)

Q19.4A

Given the reaction:

\(\mathrm{2MnO_4^-(aq) + PbO(s) + 6H^+(aq) \rightarrow 2MnO_2 (s) + 5PbO_2 (s) + 3H_2O (l)}\)

\(\mathrm{E^\circ_{cell}: +1.23\,V}\)

What does \(\mathrm{E^\circ}\) \(\ce{PbO2(s)}\) equal?

S19.4A

\(\mathrm{MnO_4^- \rightarrow MnO_2 (s)}\)

\(\mathrm{PbO (s) + 6H^+(aq) \rightarrow 2MnO_2 (s) + 3H_2O (l)}\)

\(\ce{Mn}\) oxidation number:
Reactant: +7 Product: +4
\(\Rightarrow\) \(\ce{Mn}\) is the reduction reaction: \(\ce{Mn}\) is the cathode
\(\mathrm{\Rightarrow E^\circ = 1.51}\)

\(\mathrm{E^\circ_{cell}= E^\circ_{cathode} - E^\circ_{anode}}\)
\(\mathrm{1.23= 1.51- E^\circ_{anode}}\)
\(\mathrm{E^\circ_{anode}= +0.28\,V}\)

Q19.4B

Use thermal dynamic data from Appendix D to calculate a theoretical voltage of Electrolysis cell
\(\mathrm{Cu(s) + Zn^{2+}(aq) \rightarrow Cu^{2+}(aq) + Zn(s) \quad E^\circ_{cell} =-1.103\:V}\)

S19.4B

The electrolysis is not thermodynamically favored.

\(\mathrm{E_{cell} = E_{Zn^{2+}/Zn} - E_{Cu^{2+}/Cu^+} = -0.763-0.340\,V =-1.103\,V}\)

Q19.4C

Sketch a voltaic cell for each of the following conditions, labeling the anode, cathode, and electron flow. Balance the redox equation if necessary. Calculate \(\mathrm{E^\circ_{cell}}\) for each cell.

1. \(\mathrm{Cu^{2+}(aq) + Sn^{2+}(aq) \rightarrow Cu(s) + Sn^{4+}(aq)}\)
2. \(\ce{Mg(s)}\) displaces \(\ce{Sn^2+(aq)}\) from solution
3. \(\ce{Zn(s)}\) donates e^- to acidic solution to form \(\ce{H2(g)}\)
4. \(\mathrm{Pb^{2+}(aq) +Sn(s) \rightarrow Pb(s) + Sn^{2+}(aq)}\)

Q19.5A

Determine whether a forward reaction is spontaneous or non-spontaneous:

1. \(\mathrm{Ag^{2+}(aq) + Cr^{2+}(aq) \rightarrow Ag^+ (aq)}\)
2. \(\mathrm{Sn^{4+}(aq) + 2I^-(aq) \rightarrow Sn^{2+} (aq) + I_2 (aq)}\)

S19.5A

1. \(\mathrm{E^\circ_{cell}= E^\circ_{cathode} - E^\circ_{anode}}\)

\(\mathrm{E^\circ_{cell}= (E^\circ_{Ag^{2+}/Ag^-}) - (E^\circ_{Cr^{3+}/Cr^{2+}})}\)
\(\mathrm{E^\circ_{cell}= 1.98\,V - (-0.424\,V)}\)
\(\mathrm{E^\circ_{cell}= +2.404\,V}\)
\(\mathrm{\Rightarrow Spontaneous}\)

2. \(\mathrm{Sn^{4+}(aq)\,reduced,\: 2I^-(aq)\,oxidized}\)

\(\mathrm{E^\circ_{cell} = (+0.154\,V) - (+0.535\,V)}\)
\(\mathrm{E^\circ_{cell} = -0.381\,V}\)
\(\Rightarrow \textrm{Non-spontaneous}\)

Q19.5B

A voltaic cell represented by the following cell diagram has \(\mathrm{E_{cell} = -0.119\: V}\)
\[\mathrm{Ag(s)| Ag^+(0.075\:M)|| Hg (?\: M) | Hg (l)}\]

S19.5B

Oxidation: \(\mathrm{2Ag(s) \rightarrow 2Ag^+(aq) +2e^-}\)

Reduction: \(\mathrm{Hg(aq) + 2e^- \rightarrow Hg(s)}\)

Overall: \(\mathrm{2Ag (s) + Hg^{2+}(aq) \rightarrow 2Ag^+(aq) + Hg(l)}\)

\(\begin{align}
\mathrm{E^\circ_{cell}} & = \mathrm{E^\circ_{cathode} - E^\circ_{anode}} \\
& = \mathrm{0.845\,V-0.800\,V} \\
& = \mathrm{0.054\,V}
\end{align}\)

\(\begin{align}
\mathrm{E^\circ_{cell}} & = \mathrm{E^\circ_{cathode} - E_{anode}} \\
& = \mathrm{0.854\,V-0.800\,V} \\
& = \mathrm{0.054\,V}
\end{align}\)

\(\mathrm{E = E^\circ_{cell} - \dfrac{0.0592\,V}{2}\log\dfrac{[Ag^+]^2}{?}}\)

\(\mathrm{-0.173\,V =-0.029\log\dfrac{[0.005625]}{x}}\)

\(\mathrm{5.844=\log\dfrac{[0.005625]}{x}}\)

\(\mathrm{x=0.706}\)

Q19.5C

Determine \(\mathrm{\Delta G^\circ}\) for the following voltaic cell reactions:

1. \(\mathrm{Pb^{2+}(aq) +Sn(s) \rightarrow Pb(s) +Sn^{2+}(aq)}\)
2. \(\mathrm{O_2(g) +2H^+(aq) + 2F^-(aq) \rightarrow H_2O_2(aq) + F_2(g)}\)
3. \(\mathrm{Br_2(l) +2Fe^{2+}(aq) \rightarrow 2Br^-(aq) + 2Fe^{3+}(aq)}\)

Q19.6A

Given the following voltaic cell diagram and using the standard gold electrode as the reduction half reaction, and metal \(\ce{M}\) as an oxidizing half reaction, find the \(\mathrm{E^\circ}\) reduction half reaction:

\(\begin{align}
& \mathrm{Au^{3+}(1\,M) +3e^- \rightarrow Au(s)} \quad && \mathrm E^\circ= +1.52 \\
& \mathrm{M^{3+}(1\,M) + 3e^-} \quad && \mathrm E^\circ= ?\end{align}\)

1. \(\mathrm{In \quad \hspace{5 pt} E^\circ = 1.858\: V}\)
2. \(\mathrm{Al \quad \hspace{3.5 pt}E^\circ = 3.20\: V}\)
3. \(\mathrm{La \quad E^\circ = 3.90\: V }\)
4. \(\mathrm{U \quad \hspace{5.5 pt}E^\circ = 3.18\: V}\)

S19.6A

\(\ce{Au}\) is the reduction half reaction
\(\mathrm{E^\circ= +1.52= E^\circ_{cathode}}\)
\(\mathrm{E^\circ_{cell}= E^\circ_{cathode} - E^\circ_{anode}}\)

1. \(\ce{In}\)

\(\mathrm{1.858 = +1.52- E^\circ_{anode}}\)
\(\mathrm{1.858 + E^\circ_{anode} = 1.52}\)
\(\mathrm{E^\circ_{anode}= -0.338\,V}\)

2. \(\ce{Al}\)

\(\mathrm{3.20=1.52 - E^\circ_{anode}}\)
\(\mathrm{3.20 + E^\circ_{anode} = 1.52}\)
\(\mathrm{E^\circ_{anode}= -1.68\,V}\)

3. \(\ce{La}\)

\(\mathrm{3.90 = 1.52 - E^\circ_{anode}}\)
\(\mathrm{3.90 + E^\circ_{anode} = 1.52}\)
\(\mathrm{E^\circ_{anode}= -2.38\,V}\)

4. \(\ce{U}\)

\(\mathrm{3.18 = 1.52 - E^\circ_{anode}}\)
\(\mathrm{3.18 + E^\circ_{anode}=1.52}\)
\(\mathrm{E^\circ_{anode}= -1.66\,V}\)

Q19.6B

In each of the following examples, write the cell diagram and cathode. Indicate the direction of the electron flow; write a balanced equation.

1. \(\mathrm{Al(s) +Cu^{2+} \rightarrow Cu(s) + Al^{3+}}\)
2. \(\mathrm{Fe^{3+} +Ag(s) \rightarrow Ag^+ + Fe^{2+}}\)
3. \(\mathrm{Cu(s) +2Fe^{3+} \rightarrow Cu^{2+} +2Fe^{2+}}\)

S19.6B

1. Half reaction:
   Reduction: \(\mathrm{Al(s) + 3e^- \rightarrow Al^{3+}\quad E=-2.310\,V}\)
   Oxidation: \(\mathrm{Zn^{2+} \rightarrow Zn(s) +2e^- \quad E=-0.763\,V}\)
   \(\begin{align}
   \mathrm E &= \mathrm{E_{cathode} - E_{anode}} \\
   &= \mathrm{-2.310--0.763\,V} \\
   &= \mathrm{1.447\,V}
   \end{align}\)
2. Oxidation: \(\mathrm{Fe^{3+} +e^- \rightarrow Fe^{2+} \quad E=0.771\,V}\)
   Reduction: \(\mathrm{Cu(s)\rightarrow Cu^{2+} +2e^- \quad E= 0.520\,V}\)
   \(\begin{align}
   \mathrm E &= \mathrm{E_{cathode} - E_{anode}} \\
   &= \mathrm{0.520- 0.771\,V} \\
   &= \mathrm{0.149\,V}
   \end{align}\)
3. Oxidation: \(\mathrm{Cu(s) \rightarrow Cu^{2+}+ 2e^- \quad E=0.340\,V}\)
   \(\mathrm{Fe^{3+} + e^- \rightarrow Fe^{2+} \quad E=0.771\,V}\)
   \(\begin{align}
   \mathrm E &= \mathrm{E_{cathode} - E_{anode}} \\
   &= \mathrm{0.771\,V-0.340\,V} \\
   &= \mathrm{0.431\,V}
   \end{align}\)

Q19.7A

Calculate \(\mathrm{\Delta G^\circ}\) for the following reactions and determine if spontaneous:

1. \(\mathrm{NO_3^-(aq) + Al(s) + 4H^+(aq) \rightarrow NO(g) + Al^{3+}(aq) + 2H_2O (l)}\)
2. \(\mathrm{F_2(g) + 2Li(s) \rightarrow 2F^- (aq) + 2Li^+ (aq)}\)

S19.7A

1. \(\mathrm{\Delta G^\circ= -nFE^\circ_{cell}}\)

\(\mathrm{E^\circ_{cell} = (E^\circ_{NO_3^-/NO^-}) - (E^\circ_{Al^{3+}/Al})}\)
\(\mathrm{E^\circ_{cell} = (0.956) -(-1.676)}\)
\(\mathrm{E^\circ_{cell} = 2.63\,V}\)

\(\mathrm{N = 3}\) since:

\(\ce{N}\) oxidation: reactant = +5 product= +2
\(\ce{Al}\) oxidation: reactant = 0 product= +3

\(\mathrm{F=96,485\,C/mol\,e^-}\)

\(\mathrm{\Delta G^\circ=-[(3)(96,485\,C/mol\,e^-)(2.63\,V)]}\)
\(\mathrm{\Delta G^\circ= -761\, kJ\, Spontaneous}\)

2. \(\mathrm{E^\circ_{cell} = (E^\circ_{F_2/F^-})- (E^\circ_{Li^+/Li})}\)

\(\mathrm{E^\circ_{cell} = 2.866 + 3.040 = 5.906\,V}\)

\(\mathrm{N = 2}\) since:
\(\mathrm{F_2 + 2e^- \rightarrow 2F^-}\)
\(\mathrm{2Li^+ + 2e^- \rightarrow 2Li(s)}\)

\(\mathrm{\Delta G^\circ= -[(2\,mol\,e^-)(96,485\,C/mol\,e^-)(5.906\,V)]}\)
\(\mathrm{\Delta G^\circ=-1,140\,kJ}\)
\(\mathrm{Spontaneous}\)

Q19.7B

Determine the value of the \(\mathrm{\Delta G^\circ}\) for the following reactions carried out in voltaic cells. [Use the equations of 22]

1. \(\mathrm{Al(s) + Cu^{2+} \rightarrow Cu(s) + Al^{3+}}\)
2. \(\mathrm{Fe^{3+} + Ag(s) \rightarrow Ag^+ + Fe^{2+}}\)
3. \(\mathrm{Cu(s) + 2Fe^{3+} \rightarrow Cu^{2+} +2Fe^{2+}(aq)}\)

S19.7B

To solve the problem, you have first write the balanced equation.

1. \(\mathrm{\Delta G^\circ} = \mathrm{-nFE^\circ_{cell}}\)

\(\hspace{22.5 pt}=\mathrm{-6\,mol*96485\,C\,mol^{-1}*2.106\,V}\)
\(\hspace{22.5 pt}=\mathrm{-1.2*10^6\, J}\)

2. \(\mathrm{\Delta G^\circ} = \mathrm{-nFE^\circ_{cell}}\)
   \(\hspace{22.5 pt}=\mathrm{-1\,mol* 96485\,C\,mol^{-1}*0.029\,V}\)
   \(\hspace{22.5 pt}=\mathrm{-2605.095\,V}\)

3. \(\mathrm{\Delta G^\circ} = \mathrm{-nFE^\circ_{cell}}\)
   \(\hspace{22.5 pt}=\mathrm{-2\,mol*96485\,C\,mol^{-1}*0.029\,V}\)
   \(\hspace{22.5 pt}=\mathrm{-83170.07\,J}\)

Q19.7

Write and balance the net reaction using the two following half reactions. Find the Voltage for this reaction

\(\mathrm{BrO^-(aq) + H_2O(l) + 2e^- \rightarrow Br^-(aq) +2OH^-(aq)}\)

\(\mathrm{Mg(s) + 2OH^-(aq) \rightarrow Mg(OH)_2(s) +2e^-}\)

Q19.8A

Find \(\mathrm{\Delta G^\circ}\) by combining the following half reactions to calculate the \(\mathrm{E^\circ}\) cell at:

\(\begin{align}
& \mathrm{Ag^{2+} + 2e^- \rightarrow Ag(s)} \\
& \mathrm{Ag^{2+}(aq) + e^- \rightarrow Ag^+(aq)} \quad & & \mathrm{E^\circ= +1.98\,V} \\
& \mathrm{Ag^+(aq) + e^- \rightarrow Ag(s)} \quad & & \mathrm{E^\circ= +0.800\,V}\end{align}\)

S19.8A

\(\begin{align}
& \mathrm{Ag^{2+}(aq) + e^- \rightarrow Ag^+(aq)} \quad & & \mathrm{\Delta G^\circ= -(1 \times F \times (1.98\,V))} \\
& \underline{\mathrm{Ag^+ (aq) + e^- \rightarrow Ag (s)}}\quad & & \underline{\mathrm{\Delta G^\circ= -(1 \times F \times (0.800\,V))}} \\
& \mathrm{Ag^{2+} (aq) + 2e^- \rightarrow Ag(s)} \quad & & \mathrm{\Delta G^\circ= -(1.98\,V)F - (0.800\,V)F} \\
& \, \quad & & \mathrm{\Delta G^\circ= (-2.78\,V)F}\end{align}\)

\(\mathrm{\Delta G^\circ= -nFE^\circ_{cell}}\)
\(\mathrm{(-2.78\,V)F = -2FE^\circ_{cell}}\)
\(\mathrm{E^\circ_{cell}=\dfrac{(-2.78\,V)F}{-2F}}\)
\(\mathrm{E^\circ_{cell}= +1.39\,V}\)

Q19.8B

For the reaction

\[\mathrm{Cr_2O_7^{2-}(aq) + 14H^+(aq) +6Ag(s) \rightarrow 2Cr^{3+} + 6Ag^+(aq) + 7H_2O(l)}\]

Use the data table to determine

1. \(\mathrm{E^\circ_{cell}}\)
2. \(\ce{K}\)
3. \(\mathrm{\Delta G^\circ}\)
4. Whether the reaction goes substantially to completion when the reactants and products are initially in their standard state.

S19.8B

1. Half reactions:

Cathode: \(\mathrm{Cr_2O_7^{2-} + 14H^+ +6e^- \rightarrow 2Cr^{3+} +H_2O \quad E= +1.33\,V}\)

Anode: \(\mathrm{Ag(s) \rightarrow Ag^+ + e^- \quad E=0.800\,V}\)

\(\begin{align}
\mathrm{E_{cell}} &= \mathrm{E_{cathode} - E_{anode}} \\
&= \mathrm{1.33-0.800\,V} \\
&= \mathrm{0.53\,V}
\end{align}\)

2. Standard conditions:

\(\begin{align}
\mathrm{\Delta G^\circ} &= \mathrm{-nFE^\circ_{cell}} \\
&=\mathrm{-6\,mol *96485\,C\,mol^{-1} *0.53\,V} \\
&=\mathrm{-30682.23\,V}
\end{align}\)

3. \(\mathrm{E_{cell} = - \dfrac{RT}{nF} \ln K}\)

\(\mathrm{K = e^{(-nFE_{\Large{cell}})/(RT)}}\)

\(\mathrm{K= 6.43*10^{54}}\)

4. The reaction can be spontaneous. \(\mathrm{\Delta G^\circ}\) is very negative.

Q19.9A

A voltaic cell with \(\mathrm{E_{cell}= 1.500\: V}\) has what \(\ce{[Ag+]}\) in the cell?

\(\mathrm{Zn(s)|Zn^{2+}(1.50\,M)||Ag^+(?\,M)|Ag(s)}\)

S19.9A

Solve for \(\mathrm{E_{cell}}\):

Oxidation reaction: \(\mathrm{Zn(s) \rightarrow Zn^{2+}(aq) + 2e^- \hspace{68 pt}\quad E^\circ=-0.763}\)

Reduction reaction: \(\mathrm{(Ag^+(aq)+e^- \rightarrow Ag(s))\times2 \hspace{47 pt}\quad E^\circ=0.800\,V}\)

Net Ionic Equation: \(\mathrm{Zn(s)+2Ag^+(aq) \rightarrow Zn^{2+}(aq) +2Ag(s) \quad E^\circ_{cell}=1.563\,V}\)

Use Nernst equation to solve for \(\ce{[Ag+]}\):

\(\mathrm{E=E^\circ_{cell}-\dfrac{0.0592}{2}\log\dfrac{[Zn^{2+}]}{[Ag^+]^2}}\)

\(\mathrm{1.500\,V = 1.563-\dfrac{0.0592}{2}\log\dfrac{1.5\,M}{x^2}}\)

\(\mathrm{\log\dfrac{1.5\,M}{x^2} = \dfrac{-2(1.500-1.563)}{0.0592}}\)

\(\mathrm{\log\dfrac{1.5\,M}{x^2} = 2.13}\)

\(\mathrm{x = 0.4222}\)

\(\mathrm{[Ag^+]= 0.4222\,M}\)

Q19.9B

Calculate \(\mathrm{E_{cell}}\) using the Nernst equation for the following cells.

1. \(\mathrm{Zn(s) | Zn^{2+}(aq)(0.1\,M) || Sn^{2+}(aq)(.8\,M) | Sn(s)}\)
2. \(\mathrm{Cu(s) | Cu^{+}(aq)(0.4\,M) || F^{-}(aq)(O.9\,M) | F_2(g)(0.5\,atm) | Pt(s)}\)

S19.9B

Step 1: Make half reactions and determine the oxidation and reduction equation. (Make sure equation is balanced!)

Step 2: Find the E° for each half reactions using the standard reduction potential table.

Step 3: Add the E° of both half reactions together to find the E°_cell.

Step 4: Determine the number of moles of electrons transferred (n).

Step 5: Calculate the reaction quotient (Q). \(Q= \frac{[Products]}{[Reactants]}\)

Step 6: Calculate the E_cell (Plug and chug). E_cell = E°_cell - \(\frac{0.0592V}{n}\)logQ at 298K.

a) \(\mathrm{Zn(s) | Zn^{2+}(aq)(0.1\,M) || Sn^{2+}(aq)(.8\,M) | Sn(s)}\)

ox: Zn_(s) → Zn²⁺_(aq) + 2e- E° : -0.763

Red: Sn²⁺_(aq) + 2e- → Sn_(s) E° : -0.137

E°_cell : -0.9

n=2

\(Q = \frac{[Zn^{2+}]}{[Sn^{2+}]} = \frac{0.1}{0.8} = 0.125\)

E_cell = E°_cell - \(\frac{0.0592V}{n}\)logQ = -0.9 - \(\frac{0.0592V}{n}\)log(0.125)

E_cell = -0.8733V

b) \(\mathrm{Cu(s) | Cu^{+}(aq)(0.4\,M) || F^{-}(aq)(O.9\,M) | F_2(g)(0.5\,atm) | Pt(s)}\)

Cu_(s) → Cu⁺_(aq) + e- E° = -0.340

2F^-_(aq) → F_2(g) + 2e- E° = -2.866

E°_cell = 2.186

n=2

\(Q = \frac{[Cu^{2+}]}{[F^{-}]} = \frac{0.4}{0.9} = 0.4444\)

E_cell = E°_cell - \(\frac{0.0592V}{n}\)logQ

= 2.186 - \(\frac{0.0592V}{n}\)log(0.4444)

E_cell = 2.196V

Q19.10A

\(\mathrm{[Zn^{2+}]= 1.2\,M}\)

What \(\ce{[Cu^2+]}\) will allow a forward spontaneous reaction?

Net Reaction: \(\mathrm{Zn(s) + Cu^{2+} \rightarrow Cu(s) + Zn^{2+} \quad E^\circ_{cell} = 1.100\,V}\)

S19.10A

Nernst equation setting \(\mathrm{E=0.000\,V}\) & \(\mathrm{[Zn^{2+}] =1.0\,M}\)

\(\mathrm{E=E^\circ_{cell}-\dfrac{0.0592}{2}\log\dfrac{[Zn^{2+}]}{[Cu^{2+}]}}\)

\(\mathrm{0.00\,V = 1.100-\dfrac{0.0592}{2}\log\dfrac{1.2\,M}{[Cu^{2+}]}}\)

\(\mathrm{\dfrac{0.00-1.100}{-0.0296} = \log\dfrac{1.2\,M}{[Cu^{2+}]}}\)

\(\mathrm{37.2=\log\dfrac{1.2\,M}{[Cu^{2+}]}}\)

\(\mathrm{[Cu^{2+}]= 8.4\times10^{-17}\,M}\)

Q19.10B

\(\mathrm{Pb(s) | Pb^{2+}(aq) (0.07\:M) || Fe^{3+}(aq) (0.64\:M) , Fe^{2+} (aq) (0.85\: M) | Pt(s)}\)

1. Will the cell reaction be spontaneous?
2. What ratio of \(\mathrm{\dfrac{[Pb^{2+}][Fe^{2+}]^2}{[Fe^{3+}]^2}}\) will reaction will not be spontaneous in either direction?

S19.10B

a. We are asked about the spontaneity of the reaction, which is determined by cell potentials.

We can get the standard cell potential of Pb and Fe from the chart.

Oxidation: Pb(s) → Pb²⁺ _(aq) +2e^- E^。_cell = -0.125V

Reduction: Fe³⁺_(aq) +e^- → Fe²⁺_(aq) E^。_{cell =} +0.771V

Then we can get the differences between the standard cell potentials by using the equation:

E^。_cell=E^。_reduction - E^。_oxidation

E_cell=+0.771V-(-0.125V) =0.896V

Then we use the Nerst Equation to get the cell potential in this reaction:

E_cell=E^。_cell －0.0592/2 ^. log [Pb²⁺][Fe²⁺]²/[Fe³⁺]²

=0.896V - 0.0596/2^. log [0.07M][0.85M]²/[0.64M]²

=0.896V

Thus the cell potential is positive, which indicates that the reaction is positive.

b. If the reaction is not spontaneous, then E_cell must less than 0.

Therefore, we can change the Nerst Equation into this form:

0 < E^°_{cell -} 0.0592/n ^. log [Pb²⁺][Fe²⁺]² / [Fe³⁺]²

-E^°_cell < - 0.0592/n ^. log [Pb^2+]][Fe²⁺]² / [Fe³⁺]²

E^°_cell < 0.0592/2 ^.log[Pb²⁺][Fe²⁺]² / [Fe³⁺]²

1250/37(E^o_cell) < log [Pb²⁺][Fe²⁺]² / [Fe³⁺]²

10^{(1250/37)(E_cell)} < [Pb²⁺][Fe²⁺]² / [Fe³⁺]²

10^{(1250/37)(0.869V)} < [Pb²⁺][Fe²⁺]² / [Fe³⁺]²

Thus the ratio that the reaction is not spontanoues is [Pb²⁺][Fe³⁺]² / [Fe³⁺]² > 10^{(1250/37)(0.869V)} or precisely [Pb²⁺][Fe³⁺]² / [Fe³⁺]² > 2.281 * 10²⁹

1. Oxidation: \(\mathrm{Pb(s) \rightarrow Pb^{2+}(aq) + 2e^-\hspace{10.5 pt}\quad E^\circ_{cell} = -0.125\: V}\)

Reduction: \(\mathrm{Fe^{3+}(aq)+e^- \rightarrow Fe^{2+}(aq)\quad E^\circ_{cell} = +0.771\: V}\)

\(\mathrm{E^\circ_{cell} = +0.771 \:V - (-0.125\: V) = 0.896\: V}\)

\(\begin{align} \mathrm{E_{cell}} & = \mathrm{E^\circ_{cell} - \dfrac{0.0592}{n}\log\dfrac{[Pb^{2+}][Fe^{2+}]^2}{[Fe^{3+}]^2}}\\
& = \mathrm{0.896 \:V - \dfrac{0.0592}{2}\log\dfrac{(0.07\:M)(0.85\:M)^2}{(0.64\:M)^2}}\\
& = \mathrm{0.869 \:V}\end{align}\)

Thus since \(\mathrm{E_{cell}}\) is positive, the reaction is spontaneous.

2. Ratio of \(\mathrm{\dfrac{[Pb^{2+}][Fe^{2+}]^2}{[Fe^{3+}]^2}}\) for reaction to not be spontaneous is when:

\(\mathrm{E_{cell}}\) is less than 0. Thus creating:

\(\mathrm{0 < E^\circ_{cell} - \dfrac{0.0592}{n}\log\dfrac{[Pb^{2+}][Fe^{2+}]^2}{[Fe^{3+}]^2}}\)

\(\mathrm{- E^\circ_{cell} < -\dfrac{0.0592}{n}\log\dfrac{[Pb^{2+}][Fe^{2+}]^2}{[Fe^{3+}]^2}}\)

\(\mathrm{E^\circ_{cell} < \dfrac{0.0592}{2}\log\dfrac{[Pb^{2+}][Fe^{2+}]^2}{[Fe^{3+}]^2}}\)

\(\mathrm{\dfrac{1250}{37}(E^\circ_{cell}) < \log \dfrac{[Pb^{2+}][Fe^{2+}]^2}{[Fe^{3+}]^2}}\)

\(\mathrm{10^{(1250/37)(E^\circ_{cell})} < \dfrac{[Pb^{2+}][Fe^{2+}]^2}{[Fe^{3+}]^2}}\)

\(\mathrm{10^{(1250/37)(0.869\: V)} < \dfrac{[Pb^{2+}][Fe^{2+}]^2}{[Fe^{3+}]^2}}\)

Or precisely for this cell reaction, ratio \(\mathrm{\dfrac{[Pb^{2+}][Fe^{2+}]^2}{[Fe^{3+}]^2} > 2.281 \times 10^{29}}\).

Q19.10A

1. \(\mathrm{Sn(s)|Sn^{2+}(0.080\:M)||Pb^{2+}(0.700\:M)|Pb(s)}\)

Given the following cell reaction, will the cell proceed spontaneously as written?

2. For what ratio of \(\mathrm{\dfrac{[Sn^{2+}]}{[Pb^{2+}]}}\) for the reaction above in a) will the cell not be spontaneous in either direction?

S19.10A

1. Find the \(\mathrm{E^\circ_{cell}}\) first by \(\mathrm{E^\circ_{(reduction)} - E^\circ_{(oxidation)}}\).

Oxidation: \(\mathrm{Sn(s) \rightarrow Sn^{2+}(0.080\:M) +2e^-}\) with an \(\mathrm{E^\circ_{cell}}\) of 0.137 V

Reduction: \(\mathrm{Pb^{2+}(0.700\:M) + 2e^- \rightarrow Pb(s)}\) with an \(\mathrm{E^\circ_{cell}}\) of -0.125

Thus the overall \(\mathrm{E^\circ_{cell}}\) is 0.012 V. But this cell has specific concentrations given, so we know to use the Nernst equation to find the exact \(\mathrm{E^\circ_{cell}}\).

Thus, the Nernst equation sets up as \(\mathrm{E_{cell} = 0.012\,V - \dfrac{0.0592}{2}\times\log\dfrac{[Sn^{2+}]}{[Pb^{2+}]}}\)

\(\mathrm{X= 0.012\,V - 0.0296 \log\dfrac{[0.080\,M]}{[0.700\,M]}}\)

\(\textrm{X = 0.0399 V}\)

Thus the \(\mathrm{E_{cell}}\) is positive, greater than 0, and will move spontaneously in the forward direction.

For review on this topic, visit the page "Electrochemistry 4: The Nernst Equation".

2. The \(\mathrm{E_{cell}}\) must be 0. In order for the cell not to be spontaneous in either direction, the cell must be at equilibrium.

Thus, we set up our Nernst equation again, this time designating the entire \(\mathrm{Q}\) as a variable (this is the ratio we are seeking) and set our \(\mathrm{E_{cell}}\) to 0.

This results in the following equation:

\(\mathrm{0 = 0.012\,V - \dfrac{0.0592}{2}\log [x]}\)

\(\mathrm{-0.012\,V = - 0.0296\log [x]}\)

\(\mathrm{2.54335 = x}\)

Thus the ratio must be 2.54 to ensure the cell is in equilibrium.

For any additional information, consult "Electrochemistry".

Q19.11A

A voltaic cell:

\(\mathrm{Ag(s)|Ag^+(saturated\:Ag_2CrO_4)||Ag^+(0.125\,M)|Ag(s)}\)

What is \(\mathrm{E_{cell}}\) if \(\mathrm{K_{sp}=1.2\times10^{-11}}\) for \(\ce{Ag2CrO4}\)?

S19.11B

First must solve for \(\mathrm{[Ag^+]}\) in saturated solution

\(\mathrm{K_{sp}= [Ag^+]^2[CrO_4^{2-}] = (2s)^2(s) = 4s^3}\)

\(\mathrm{S = \sqrt[\Large 3]{\dfrac{1.2\times10^{-11}}{4}} = 1.44\times10^{-4}\, M}\)

\(\mathrm{[Ag^+]_{anode} = 2s = 2.88\times10^{-4}\,M}\)

\(\mathrm{Ag(s)+Ag^+(0.125\,M)\rightarrow Ag(s)+Ag^+(2.88\times 10^{-4}\,M)}\)

\(\mathrm{E_{cell}=E^\circ_{cell}-\dfrac{0.0592}{2}\log\dfrac{2.88\times10^{-4}\,M}{0.125\,M}}\)

\(\mathrm{E_{cell}=0.000+0.078\,V =0.078\,V}\)

Q19.11B

Predict whether spontaneous reaction in forward direction will occur at 298K for reaction:

1. \(\mathrm{Cu(s) + Br_2(l) \rightarrow Cu^{2+}(aq)+2Br^-(aq)}\)
2. \(\mathrm{Sn^{2+}(aq) + Pb^{2+}(aq) \rightarrow Pb(s) + Sn^{4+}(aq)}\)
3. \(\mathrm{2Ag(s) + 2H^+(aq) \rightarrow 2Ag^+(aq) + H_2(g)}\)
4. \(\mathrm{2Cl_2(g)+ 2H_2O(l) \rightarrow 4HCl (aq) + O_2(g)}\)

S19.11B

Formula: \(\mathrm{E^{\circ}_{cell} = E^{\circ}_{cathode} - E^{\circ}_{anode}}\)

Oxidation occurs at anode. Reduction occurs at cathode.

Positive \(\mathrm{E^\circ_{cell}}\) = spontaneous reaction at temperature given.

1. Anode: \(\mathrm{Cu(s) \rightarrow Cu^{2+}(aq) + 2e^- \hspace{8 pt}\quad E^{\circ}_{cell} = +0.340\:V}\)

Cathode: \(\mathrm{Br_2(l) + 2e^- \rightarrow 2Br^-(aq)\quad E^{\circ}_{cell}= +1.065\:V}\)

\(\mathrm{E^{\circ}_{cell} = +1.065\:V - 0.340\:V =+0.725\:V}\). Spontaneous reaction at 298K.

2. Anode: \(\mathrm{Sn^{2+}(aq) \rightarrow Sn^{4+}(aq) + 2e^- \quad E^{\circ}_{cell}= +0.154\:V}\)

Cathode: \(\mathrm{Pb^{2+}(aq) + 2e^- \rightarrow Pb(s) \hspace{3 pt}\quad E^\circ_{cell}= -0.125\:V}\)

\(\mathrm{E^{\circ}_{cell} = -0.125\:V - 0.154\:V = -0.279\:V}\). Non-spontaneous at 298K.

3. Anode: \(\mathrm{2Ag(s) \rightarrow 2Ag^+(aq) + 2e^-\quad E^\circ_{cell} = +0.800\:V}\)

Cathode: \(\mathrm{2H^+(aq) + 2e^- \rightarrow H_2(g)\hspace{1 pt}\quad E^\circ_{cell} = 0.000\:V}\)

\(\mathrm{E^\circ_{cell} = 0.000\:V - 0.800\:V =-0.800\:V}\). Non-spontaneous at 298K.

4. Anode: \(\mathrm{2H_2O(l) \rightarrow 4H^+(aq) + O_2(g) + 4e^- \quad E^\circ_{cell} = +1.229\:V}\)

Cathode: \(\mathrm{2Cl_2(l) + 4e^- \rightarrow 4Cl^-(aq)\hspace{36 pt}\quad E^\circ_{cell}= +1.358\:V}\)

\(\mathrm{E^{\circ}_{cell} = +1.358\:V - (+1.229\:V) = +0.129\:V}\). Spontaneous reaction at 298K.

Q19.11C

All reactants and products are in their standard states, and use data from the standard electrode reduction potentials table to predict whether the reaction is spontaneous in the forward reaction:

1. \(\mathrm{Cu (s) + 2Ag^+ (aq) \rightarrow Cu^{2+} (aq) + 2Ag (s)}\)
2. \(\mathrm{2Al (s) + 3Zn^{2+} (aq) \rightarrow 2Al^{3+} (aq) + 3Zn (s)}\)
3. \(\mathrm{Fe^{2+} (aq) + Ag^+ (aq) \rightarrow Fe^{3+} (aq) + Ag (s)}\)
4. \(\mathrm{2Fe^{2+} (aq) + I_2 (s) \rightarrow 2Fe^{3+} (aq) + 2I^- (aq)}\)

S19.11C

1. Cell reaction: \(\mathrm{Cu(s) + 2Ag^+ (aq) \rightarrow 2Cu^{2+} (aq) + 2Ag (s)}\)

We must split up the overall reaction into balanced half reactions, which is why we multiply Ag by 2. We have to have equal amounts of electrons on both sides so that they cancel. The placement of electrons on the charged sides of the half reactions balances the charges to 0. We must reach 0 because the elemental versions of Cu and Ag have a charge of 0. After we form the half reactions, we must determine the cathode and the anode because E^ocell=E^o(cathode)-E^o(anode). In other words, the anode is the oxidized portion and the cathode is the reduced portion. Oxidized means we lost electrons and reduced means we gained electrons.

Oxidation: \(\mathrm{ Cu (s) \rightarrow Cu^{2+} + 2e^-}\) Lost electrons
Reduction: \(\mathrm{(Ag^+ (aq) + e^- \rightarrow Ag (s))\times2}\) Gained Electrons

\(\begin{align}
\mathrm{E^\circ_{cell}} & = \mathrm{E^\circ_{(reduction)}-E^\circ_{(oxidation)}} \\
& =\mathrm{E^\circ_{Ag^+/Ag} - E^\circ_{Cu/Cu^{2+} }} \\
& =\mathrm{0.7991-0.3394= +0.4597\:V}
\end{align}\)
These values are taken off the Reduction Half-Reactions chart. To use this chart, we must find the half reaction used and enter the value in V shown depending on the orientation listed. In this case we take the 0.7991 of Ag+ and subtract 0.3394 of Cu. Our result is a positive 0.4597 V.
The cell potential is positive, therefore the spontaneous reaction will occur in the forward reaction.

2. Cell reaction: \(\mathrm{2Al (s) + 3Zn^{2+} (aq) \rightarrow 2Al^{3+} (aq) + 3Zn (s)}\)
   
   We must split up the overall reaction into balanced half reactions, which is why we multiply Al by 2 and Zn by 3. We have to have equal amounts of electrons on both sides so that they cancel. The placement of electrons on the charged sides of the half reactions balances the charges to 0. We must reach 0 because the elemental versions of Al and Zn have a charge of 0. After we form the half reactions, we must determine the cathode and the anode because E^ocell=E^o(cathode)-E^o(anode). In other words, the anode is the oxidized portion and the cathode is the reduced portion. Oxidized means we lost electrons and reduced means we gained electrons.

Oxidation: \(\mathrm{(Al (s) \rightarrow Al^{3+} + 3e^- )\times2}\) Lost Electrons
Reduction: \(\mathrm{(Zn^{2+}(aq) +2e^-\rightarrow Zn(s) )\times3}\)
\(\begin{align} Gained Electrons
\mathrm{E^\circ_{cell}} & = \mathrm{E^\circ_{(reduction)}-E^\circ_{(oxidation)}} \\
& =\mathrm{E^\circ_{Zn^{2+}/Zn} - E^\circ_{Al/Al^{3+}}} \\
& =\mathrm{-0.7621-(-1.676)= +0.9139\:V}
\end{align}\)
These values are taken off the Reduction Half-Reactions chart. To use this chart, we must find the half reaction used and enter the value in V shown depending on the orientation listed. In this case we take the -0.7621 of Zn2+ and subtract -1.676 of Al. Our result is a positive 0.09139V.
The cell potential is positive, therefore the spontaneous reaction will occur in the forward reaction.

3. Cell reaction: \(\mathrm{Fe^{2+}(aq) + Ag^+ (aq) \rightarrow Fe^{3+} (aq) + Ag (s)}\)
   
   We must split up the overall reaction into balanced half reactions. We have to have equal amounts of electrons on both sides so that they cancel. The placement of electrons on the charged sides of the half reactions balances the charges to 0. We must reach 0 because the elemental versions of Ag and Fe have a charge of 0. After we form the half reactions, we must determine the cathode and the anode because E^ocell=E^o(cathode)-E^o(anode). In other words, the anode is the oxidized portion and the cathode is the reduced portion. Oxidized means we lost electrons and reduced means we gained electrons.

Oxidation: \(\mathrm{Fe^{2+} (aq) \rightarrow Fe^{3+} (aq) + e^- }\) Lost electrons
Reduction: \(\mathrm{Ag(s)\rightarrow Ag^+(aq) + e^-}\)
\(\begin{align} Gained electrons
\mathrm{E^\circ_{cell}} & = \mathrm{E^\circ_{(reduction)}-E^\circ_{(oxidation)}} \\
& =\mathrm{E^\circ_{Ag^+/Ag} - E^\circ_{Fe^{2+}/Fe^{3+}}} \\
& =\mathrm{0.7991-0.769= +0.0301\:V}
\end{align}\)
These values are taken off the Reduction Half-Reactions chart. To use this chart, we must find the half reaction used and enter the value in V shown depending on the orientation listed. In this case we take the 0.7991 of Ag+ and subtract 0.769 of Fe2+. Our result is a positive 0.0301V.
The cell potential is positive, therefore the spontaneous reaction will occur in the forward reaction.

4. Cell reaction: \(\mathrm{2Fe^{2+}(aq) + I_2(s) \rightarrow 2Fe^{3+}(aq) + 2I^- (aq)}\)
   
   We must split up the overall reaction into balanced half reactions, which is why we must multiply Fe by 2. We have to have equal amounts of electrons on both sides so that they cancel. The placement of electrons on the charged sides of the half reactions balances the charges to 0. We must reach 0 because the elemental versions of I and Fe have a charge of 0. After we form the half reactions, we must determine the cathode and the anode because E^ocell=E^o(cathode)-E^o(anode). In other words, the anode is the oxidized portion and the cathode is the reduced portion. Oxidized means we lost electrons and reduced means we gained electrons.

Oxidation: \(\mathrm{(Fe^{3+}(aq) + e^- \rightarrow Fe^{2+}(aq))\times2}\) Lost electrons
Reduction: \(\mathrm{I_2(s) + 2e^- \rightarrow 2I^-(aq)}\)
\(\begin{align} Gained electrons
\mathrm{E^\circ_{cell}} & = \mathrm{E^\circ_{(reduction)}-E^\circ_{(oxidation)}} \\
& =\mathrm{E^\circ_{I_2/2I^-} - E^\circ_{Fe^{2+}/Fe^{3+}}} \\
& =\mathrm{0.535-0.769= -0.234\:V}
\end{align}\)
These values are taken off the Reduction Half-Reactions chart. To use this chart, we must find the half reaction used and enter the value in V shown depending on the orientation listed. In this case we take the 0.535 of I2 and subtract 0.769 of Fe2+. Our result is a negative -0.234V. Since the half reaction for Fe2+ is flipped on the chart and yields a negative V, we must change it to a positive. This gives us the correct value for the correct direction of the reaction and results in an overall negative -0.234V.
The cell potential is negative, therefore the spontaneous reaction will not occur in the forward reaction.

Below is a partial image of the chart we must use to come to these conclusions:


Here is a link to a video that solves examples of E^o cell under nonstandard conditions for additional help:

www.youtube.com/watch?v=62rEVSBBJMw

Q19.11D

You may assume that the reactants and products in the equations are in their standard states. Use the information from Table P2 to predict if a spontaneous reaction will occur in the forward direction as drawn for the following cases.

1. \(\mathrm{ Zn (s) + Cu^{2+} \rightarrow Zn^{2+} + Cu (s)}\)
2. \(\mathrm{2Hg^{2+} (aq) + 2Br^- (aq) \rightarrow Hg_2^{2+}(aq) + Br_2 (l)}\)
3. \(\mathrm{2Fe^{2+} (aq) + Cl_2 (g) \rightarrow 2Fe^{3+}(aq) + 2Cl^-(aq)}\)

S19.11D

1. The \(\mathrm{E^{\circ}_{cell} = E^{\circ}_{(\textrm{reduction half-cell})} - E^{\circ}_{(\textrm{oxidation half-cell})} = 0.340 V - (-0.763 V)= 1.103 V}\). Because the \(\mathrm{E^\circ_{cell}}\) is positive, the direction of spontaneous change is in the forward reaction. Recognize that \(\ce{Cu^2+}\) is the stronger oxidizing agent (see Table P2) and will be more likely to be reduced. Thus, the \(\ce{Cu^2+}\) half reaction is where copper is reduced and will be the reduction half-cell. The \(\ce{Zn^2+}\)half reaction will be the oxidation half-cell because Zinc gets oxidized at the anode.
2. The \(\mathrm{E^{\circ}_{cell} = E^{\circ}_{(\textrm{reduction half-cell})} - E^{\circ}_{(\textrm{oxidation half-cell})} = 0.911 V - 1.087 V = -0.126 V}\). Because the \(\mathrm{E^\circ_{cell}}\) is negative, the direction of spontaneous change is in the reverse direction.
3. The \(\mathrm{E^{\circ}_{cell} = E^{\circ}_{(\textrm{reduction half-cell})} - E^{\circ}_{(\textrm{oxidation half-cell})} = \mathrm{1.358 V - 0.771 V= 0.587V }}\). Because the \(\mathrm{E^\circ}\) is positive, the direction of spontaneous change is in the forward direction. Recognize that the reduction of chlorine takes place at the cathode, making it the reduction half-cell. The oxidation of iron occurs at the anode, making it the oxidation half-cell.

Q19.12A

Describe what would happen to a nail that is in a mixture which demonstrates a pink color if there is a base present and a blue color in the presence of Turbull's blue \(\ce{KFe[Fe(CN)6]}\) in each situation:

1. Copper wire is wrapped around the tip of the nail
2. The center of the nail has the outer layer filed off
3. The nail is coated with \(\ce{Zn}\) (galvination)

S19.12A

1. Iron is a stronger reducing agent than copper and so blue precipitate will form in the areas not covered by copper (oxidation will occur). Hydroxide would be produced at the cathode (copper wire) and pink will form.
2. Newly exposed metal will oxidize producing a blue precipitate.
3. The zinc will oxidize rather than the iron producing hydroxide ions (pink color).

Q19.13A

An aqueous solution containing the following ions has 2.15 A of current passed through for 60 min, how much metal (in g) is formed at the cathode in each solution?

1. \(\ce{Zn^2+}\)
2. \(\ce{Al^3+}\)
3. \(\ce{Ag+}\)
4. \(\ce{Ni^2+}\)]

S19.13A

First calculate charge passed through and number of moles of electrons transferred:

\(\mathrm{Mol\:e^- = 60\:min \times\dfrac{60\:s}{1\:min}\times\dfrac{2.15\:C}{1\: s}\times\dfrac{1\:mol\:e^-}{96485\:C} = 0.08\:mol\:e^-}\)

1. \(\ce{Zn^2+}\)

\(\mathrm{0.08\:mol\:e^- \times \dfrac{1\:mol\:Zn^{2+}}{2\:mol\:e^-}\times\dfrac{1\:mol\:Zn}{1\:mol\:Zn^{2+}}\times\dfrac{65.39\:g\:Zn}{1\:mol\:Zn} = 2.62\:g\:Zn}\)

2. \(\ce{Al^3+}\)

\(\mathrm{0.08\:mol\: e^- \times \dfrac{1\:mol\: Al^{3+}}{3\: mol\: e^-} \times\dfrac{1\: mol\: Al}{1\:mol\: Al^{3+}}\times\dfrac{26.98\:g\:Al}{1\:mol\:Al} = 0.72\:g\:Al}\)

3. \(\ce{Ag+}\)

\(\mathrm{0.08\:mol\: e^- \times\dfrac{1\: mol\: Ag^+}{1\: mol\: e^-}\times\dfrac{1\: mol\: Ag}{1\: mol\:Ag^+}\times\dfrac{107.9\:g\: Al}{1\: mol\: Ag}= 8.63\:g\:Ag}\)

4. \(\ce{Ni^2+}\)

\(\mathrm{0.08\:mol\: e^- \times\dfrac{1\: mol\: Ni^{2+}}{2\: mol\: e^-} \times\dfrac{1\: mol\: Ni}{1\: mol\: Ni^{2+}}\times\dfrac{58.69\:g\: Ni}{1 \:mol\: Ni}= 2.35\:g\: Ni}\)

Q19.14A

What voltage is required for the electrolysis of the following reactions? All reactants are in standards states.

1. \(\mathrm{Zn(s) + Sn^{2+}(aq) \rightarrow Zn^{2+}(aq) + Sn(s)}\)
2. \(\mathrm{2Fe^{2+}(aq) + Hg^{2+}(aq) \rightarrow 2Fe^{3+}(aq) + Hg(l)}\)
3. \(\mathrm{Cu(s) + Sr^{2+}(aq) \rightarrow Cu^{2+}(aq) + Sr(s)}\)

S19.14A

1. Oxidation reaction: \(\mathrm{Zn(s) \rightarrow Zn^{2+}(aq) + 2e^- \hspace {37 pt}\quad E^\circ_{cell}= -0.763\:V}\)

Reduction reaction: \(\mathrm{Sn^{2+}(aq) + 2e^- \rightarrow Sn(s) \hspace {34 pt}\quad E^\circ_{cell}= -0.137\:V}\)

Net reaction: \(\mathrm{Zn(s) + Sn^{2+}(aq) \rightarrow Zn^{2+}(aq) + Sn(s) \quad E^\circ_{cell}= 0.626\:V}\)

This reaction is spontaneous

2. Oxidation reaction: \(\mathrm{2Fe^{2+} \rightarrow 2Fe^{3+} + 2e^- \hspace{74 pt}\quad E^\circ_{cell}= 0.771\:V}\)

Reduction reaction: \(\mathrm{Hg^{2+}(aq) + 2e^- \rightarrow Hg(l) \hspace{58 pt}\quad E^\circ_{cell}= 0.854\:V}\)

Net reaction: \(\mathrm{2Fe^{2+}(aq) + Hg^{2+}(aq) \rightarrow 2Fe^{3+}(aq) + Hg(l) \quad E^\circ_{cell}= 0.083\: V}\)

This reaction is spontaneous

3. Oxidation reaction: \(\mathrm{Cu(s) \rightarrow Cu^{2+}(aq) + 2e^- \hspace{53 pt}\quad E^\circ_{cell}= 0.337\:V}\)

Reduction reaction: \(\mathrm{Sr^{2+}(aq) + 2e^-(aq) \rightarrow Sr(s) \hspace{37 pt}\quad E^\circ_{cell}= -2.89\:V}\)

Net reaction: \(\mathrm{Cu(s) + Sn^{4+}(aq) \rightarrow Cu^{2+}(aq) + Sn^{2+}(aq)\quad E^\circ_{cell}= -3.227\:V}\)

Reaction requires voltages \(\mathrm{> 3.227\: V}\)

Q19.15A

\(\mathrm{N_2H_4(aq) + O_2(g) \rightarrow N_2(g) + 2H_2O(l)\quad E^\circ_{cell}=1.559\:V}\)

Calculate \(\mathrm{\Delta G^\circ_f}\) for \(\ce{[N2H4(aq)]}\)

S19.15A

Calculate \(\mathrm{\Delta G^\circ_f= -nFE^\circ_{cell} = -4\:mol\:e^- \times \dfrac{96485\: C}{1\: mol\: e^-}\times1.559\:V = -6.017\times10^5\: J = -601.7\: kJ}\)

Find \(\mathrm{\Delta G^\circ_f}\) for (\(\ce{N2H4}\)):

\(\mathrm{-601.7\:kJ = \Delta G^\circ_f[N_2(g)] + 2 \Delta G^\circ_f[H_2O(l)] - \Delta G^\circ_f[N_2H_4(aq)] - \Delta G^\circ_f[O_2(g)]}\)

\(\mathrm{-601.7\:kJ = 0.00\:kJ + 2(-237.2) + 601.7 = 127.3\: kJ}\)

For more information on calculating \({E'_{cell}}\) check out The Cell Potential.

For more info on calculating \({E_{cell}}\) check out Nernst Equation and Electrochemical Cells under Nonstandard Conditions.

Q19.16A

Find the weight of \(\ce{MnO2}\) in grams from the following overall reaction knowing that the voltmeter reading at non standard state is 0.25V, the pH of the solution is 6 and the solution is diluted to 0.6L.

\(\mathrm{Pt(s)|Cr^{3+}(0.2\:M),Cr_2O_7^{2-}(0.15\:M)||MnO_4(x\:M)|MnO_2(s)}\)

S19.16A

\(\begin{align}
& \textrm{Reduction: } \ce{2MnO4- (aq) + 8H+ (aq) + 6e- \rightarrow 2MnO2(s) + 2H2O(l)}
& & \mathrm{E^{\circ}=+1.51\:V} \\
& \textrm{Oxidation: } \ce{2Cr^3+ (aq) + 7H2O(l) \rightarrow Cr2O7^2- (aq) + 14H+ (aq) + 6e-}
& & \mathrm{E^{\circ}=+1.33\:V} \end{align}\)

\(\begin{align}
\mathrm{E^{\circ}_{cell}} & = \mathrm{E^{\circ}_{reduction}- E^{\circ}_{oxidation}} \\
& = \mathrm{1.51-1.33} \\
& = \mathrm{0.18\:V}
\end{align}\)

Apply Nernst Equation:

\(\mathrm{E_{cell}= E^{\circ}_{cell}-\dfrac{0.0592\:V}{n}\log Q}\)

\(\mathrm{0.25=0.18-\dfrac{0.0592\:V}{6}\log\dfrac{[H^+]^6[Cr_2O_7^{2-}]}{[Cr^{3+}][MnO_4^-]^2}}\)

\(\mathrm{-10.135= \log\dfrac{[H^+]^6[Cr_2O_7^{2-}]}{[Cr^{3+}][MnO_4^-]^2}}\)

\(\mathrm{7.3\times10^{-11}=\dfrac{[H^+]^6[Cr_2O_7^{2-}]}{[Cr^{3+}][MnO_4^-]^2}}\)

\(\mathrm{7.3\times10^{-11}=\dfrac{[10^{-6}]^6[0.15]}{[0.2][MnO_4^-]^2}}\)

\(\mathrm{[MnO_4^-]^2=2.2\times10^{-48}}\)

\(\mathrm{[MnO_4^-]=1.48\times10^{-24}}\)

Mass of \(\ce{MnO2}\) produced: \(\mathrm{0.6\:L\times\dfrac{1.48\times10^{-24}}{1\:L\: of\: solution}\times\dfrac{2\:mol\: MnO_2}{2\:mol\: MnO_4^-}\times\dfrac{86.94\:g\: MnO_2}{1\:mol\: MnO_2}}\)

\(\mathrm{=7.73\times10^{-23}\:g\: of\: MnO_2\: produced}\)

Q19.17A

1. Identify the value of the \(\href{/Analytical_Chemistry/Electrochemistry/Voltaic_Cells#Cell_Voltage.2fCell_Potential}{\mathrm{E^\circ_{cell}}}\) of the following reaction, and indicate if the reaction takes place spontaneous or nonspontaneously.

\(\mathrm{I_2(s)|I^-(0.6\:M)||Br_2(l)|Br^-(0.80\:M)|Pt(s)}\)

2. What is the minimum ratio of \(\mathrm{\dfrac{[Br^-]^2}{[I^-]^2}}\) for this reaction to be spontaneous?

S19.17A

1. Reduction: \(\ce{Br2(l) + 2e- \rightarrow Br- (aq)} \quad \mathrm{E^{\circ}=+1.065\:V}\)
   Oxidation: \(\ce{2I- (aq) \rightarrow I2(s) + 2e-} \quad \hspace{11 pt} \mathrm{E^{\circ}= +0.535\:V}\)
   Overall: \(\ce{Br2(l) + 2I- (aq) \rightarrow 2Br- (aq) + I2(s)}\)

\(\begin{align}
\mathrm{E^{\circ}_{cell}} & = \mathrm{E^{\circ}_{reduction}- E^{\circ}_{oxidation}} \\
& = \mathrm{1.065-0.535} \\
& = \mathrm{0.530\:V}
\end{align}\)

Apply Nernst Equation:

\(\begin{align}
\mathrm{E_{cell}} & = \mathrm{E^{\circ}_{cell}-\dfrac{0.0592\:V}{n}\log Q} \\
& = \mathrm{0.53-\dfrac{0.0592\:V}{2}\log\dfrac{[Br^-]^2}{[I^-]^2}} \\
& = \mathrm{0.53-\dfrac{0.0592\:V}{2}\log\dfrac{[0.8]^2}{[0.6]^2}} \\
& = \mathrm{0.523\:V}
\end{align}\)

Since \(\mathrm{E_{cell} > 0}\), \(\mathrm{\Delta G^\circ < 0}\). Therefore, the reaction is spontaneous.

2. Set \(\mathrm{E_{cell}= 0}\)

Apply Nernst Equation:

\(\mathrm{E_{cell}= E^{\circ}_{cell}-\dfrac{0.0592\:V}{n}\log Q}\)

\(\mathrm{0=0.53\:V-\dfrac{0.0592\:V}{2}\log\dfrac{[Br^-]^2}{[I^-]^2}}\)

\(\mathrm{17.9=\log\dfrac{[Br^-]^2}{[I^-]^2}}\)

\(\mathrm{\dfrac{[Br^-]^2}{[I^-]^2}=8.04\times10^{17}\,M}\)

Q19.19A

Write cell reactions for the electrochemical cells diagrammed, and use data from the table of standard electrode potentials to calculate \(\mathrm{E^\circ_{cell}}\) for each reaction.

1. \(\mathrm{Fe (s)|Fe^{2+} (aq)||Zn^{2+} | Zn (s)(aq)}\)
2. \(\mathrm{Na(s)|Na^+(aq)||Cl_2(g)|Cl^-(aq)}\)
3. \(\mathrm{Co(s)|Co^{2+} (aq)||Mn^{2+} (aq)|Mn(s)}\)
4. \(\mathrm{Pt(s)|Fe^{2+} (aq), Fe^{3+} (aq)||Pb^{2+}(aq)|Pb(s)}\)

S19.19A

1. Oxidation: \(\mathrm{Fe(s) \rightarrow Fe^{2+} (aq) + 2e^- \hspace{74 pt} \quad E^\circ = -(-0.440\:V)}\)

Reduction: \(\mathrm{Zn^{2+} (aq) + 2e^- \rightarrow Zn(s) \hspace{68 pt} \quad E^\circ = -0.7621\:V}\)
Net Reaction: \(\mathrm{Fe(s) + Zn^{2+} (aq) \rightarrow Fe^{2+} (aq) + Zn(s) \quad E^\circ_{cell}= -0.3321\: V}\)

2. Oxidation: \(\mathrm{(Na(s) \rightarrow Na^+ (aq) + e^-) \times 2 \hspace{83 pt}\quad E^\circ = -(-2.7144\:V)}\)

Reduction: \(\mathrm{Cl_2 (g) +2e^- \rightarrow 2Cl^-(aq) \hspace{73 pt}\quad E^\circ = 1.3601\:V}\)
Net Reaction: \(\mathrm{Na(s) + Cl_2(g) \rightarrow Na^+ (aq) + 2Cl^-(aq) \quad E^\circ_{cell}=+4.0745\:V}\)

3. Oxidation: \(\mathrm{Co(s) \rightarrow Co^{2+} (aq) + 2e^- \hspace{80 pt}\quad E^\circ= -(-0.277\:V)}\)

Reduction: \(\mathrm{Mn^{2+} (aq) + 2e^- \rightarrow Mn(s) \hspace{71 pt}\quad E^\circ = -1.182\:V}\)
Net Reaction: \(\mathrm{Co(s) + Mn^{2+} (aq) \rightarrow Co^{2+} (aq) + Mn(s) \quad E^\circ_{cell}= -0.905\:V}\)

4. Oxidation: \(\mathrm{(Fe^{2+} (aq) \rightarrow Fe^{3+} (aq) + e^-)\times2 \hspace{47 pt}\quad E^\circ= -(+0.771\:V)}\)

Reduction: \(\mathrm{Pb^{2+} (aq) + 2e^- \rightarrow Pb(s) \hspace{76 pt}\quad E^\circ= -0.125\:V}\)
Net Reaction: \(\mathrm{2Fe^{2+} + Pb^{2+}(aq) \rightarrow 2Fe^{3+} (aq) + Pb(s) \quad E^\circ_{cell} = -0.896\:V}\)

Q19.19B

Write cell reaction and calculate its \(\mathrm{E^\circ_{cell}}\)_.

1. \(\mathrm{Al(s)|Al^{3+}(aq)||Pb^{2+}(aq)|Pb(s)}\)
2. \(\mathrm{Na(s) |Na^+(aq) || Mn^{2+} (aq)| Mn(s)}\)
3. \(\mathrm{Li (s) | Li^+(aq) || F_2(g) | F^-(aq) | Pt(s)}\)
4. \(\mathrm{Pt(s)| Fe^{2+}(aq),\,Fe^{3+}(aq) || Cu^{2+}(aq) |Cu(s)}\)

S19.19B

1. Anode/Oxidation: \(\mathrm{Al(s) \rightarrow Al^{3+}(aq) + 3e^-\hspace{16 pt}\quad E^\circ_{cell} = -1.676\:V}\)

Cathode/Reduction: \(\mathrm{Pb^{2+}(aq) + 2e^- \rightarrow Pb(s)\quad E^\circ_{cell} = -0.125\:V}\)

Overall: \(\mathrm{3Pb^{2+}(aq) + 2Al(s) \rightarrow 2Al^{3+}(aq) + 3Pb(s) }\)

\(\mathrm{E^\circ_{cell} = -0.125\:V - (-1.676\:V) =+1.551\:V}\)

2. Anode: \(\mathrm{Na(s)\rightarrow Na^+(aq) + e^- \hspace{21 pt} \quad E^\circ_{cell} = -2.7144\:V}\)

   Cathode: \(\mathrm{Mn^{2+}(aq) + 2e^- \rightarrow Mn(s)\quad E^\circ_{cell} = -1.182\:V}\)

Overall: \(\mathrm{Mn^{2+}(aq) + 2Na (s) \rightarrow Mn(s) + 2Na^+(aq) }\)

\(\mathrm{E^\circ_{cell} = -1.182\:V -(-2.7144\:V) =+1.5324\:V}\)

3. Anode: \(\mathrm{Li(s) \rightarrow Li^+(aq) + e^- \hspace{21 pt}\quad E^\circ_{cell} = -3.040\:V}\)

Cathode: \(\mathrm{F_2(g) + 2e^- \rightarrow 2F^-(aq)\quad E^\circ_{cell}=+2.866\:V }\)

Overall: \(\mathrm{2Li(s) + F_2(g) + \rightarrow 2F^-(aq) + 2Li^+(aq)}\)

\(\mathrm{E^\circ_{cell} = +2.866\:V - (-3.040\:V) = +5.906\:V}\)

4. Anode: \(\mathrm{Fe^{2+} (aq) \rightarrow Fe^{3+} (aq) + e^- \hspace{9 pt}\quad E^\circ_{cell} = 0.771\:V}\)

Cathode: \(\mathrm{Cu^{2+}(aq) + 2e^- \rightarrow Cu(s)\hspace{2 pt} \quad E^\circ_{cell} = +0.340\:V}\)

Overall: \(\mathrm{Cu^{2+}(aq) + 2Fe^{2+} (aq) \rightarrow Cu(s) + 2Fe^{3+}(aq)}\)

\(\mathrm{E^\circ_{cell} = +0.340\:V - (0.771\:V) = -0.431\:V }\)

Q19.19C

Write the cell reactions for the electrochemical cells provided below. Then use data from Table Table P2 calculate \(\mathrm{E^\circ_{cell}}\) for each of the reactions.

1. \(\mathrm{Ag(s)|Ag^+ (aq)||Hg^{2+} (aq)|Hg(l)}\)
2. \(\mathrm{Al (s)|Al^{3+}(aq)||Zn^{2+} (aq)|Zn(s)}\)
3. \(\mathrm{Pt|Ce^{4+}(aq),Ce^{3+}(aq) || I^-(aq), I_2(s)| C(s)}\)
4. \(\mathrm{Mg(s)|MCg^{2+}||2H^+(aq)|H_2(g)}\)

S19.19

1. Oxidation: \(\mathrm{2Ag(s) \rightarrow 2Ag^+(aq) + 2e^-}\)

Reduction: \(\mathrm{Hg^{2+}(aq) + 2e^- \rightarrow Hg(l)}\)

Overall: \(\mathrm{2Ag(s) + Hg^{2+}(aq) \rightarrow 2Ag^+(aq) + Hg(l)}\)

\(\begin{align}\mathrm{E^{\circ}_{cell}} & = \mathrm{E^{\circ}_{(\textrm{reduction half-cell})} - E^{\circ}_{(\textrm{oxidation half-cell})}} \\ & =\mathrm{0.854\; V -(0.800\;V) = 0.054\;V} \end{align}\)

2. Oxidation: \([\mathrm{Al (s) \rightarrow Al^{3+}(aq) + 3e^-}]\times2\)

Reduction: \([\mathrm{Zn^{2+}(aq) + 2e^- \rightarrow Zn(s)}]\times3\)

Overall: \(\mathrm{2Al (s) + 3Zn^{2+}(aq) \rightarrow 2Al^{3+}(aq) + 3Zn(s)}\)

\(\begin{align}\mathrm{E^{\circ}_{cell}} & = \mathrm{E^{\circ}_{(\textrm{reduction half-cell})} - E^{\circ}_{(\textrm{oxidation half-cell})}} \\ & =\mathrm{-0.763 -(-1.676) = 0.913\;V} \end{align}\)

3. Oxidation: \(\mathrm{I_2(s) \rightarrow 2I^-(aq) + 2e^-}\)

Reduction: \([\mathrm{Ce^{4+} + e^- \rightarrow Ce^{3+}}]\times2\)

Overall: \(\mathrm{2Ce^{4+} + I_2(s) \rightarrow 2Ce^{3+}+ 2I^-(aq)}\)

\(\mathrm{E^{\circ}= 1.44 - 0.54 = 0.90\;V}\)

4. Oxidation: \(\mathrm{Mg(s) \rightarrow Mg^{2+}(aq) + 2e^-}\)

Reduction: \(\mathrm{2H^+ (aq) + 2e^- \rightarrow H_2(g)}\)

Overall: \(\mathrm{Mg(s) + 2H^+(aq) \rightarrow Mg^{2+}(aq)+ H_2(g)}\)

\(\mathrm{E^{\circ} = 0 - (-2.372) = 2.372\;V}\)

For review on this topic, visit the page "Electrochemistry 2: Galvanic cells and electrodes".

Q19.22A

For each of the following reactions below, draw a voltaic cell. In your drawing include the anode, cathode, and show the flow of electrons. Balance the equation and calculate the \(\mathrm{E^\circ_{cell}}\).

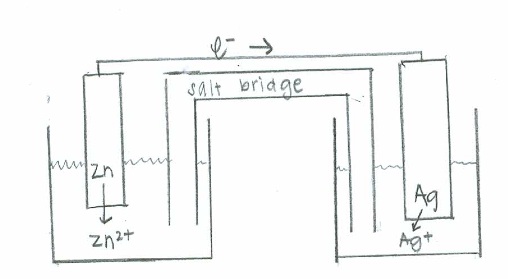
1. \(\mathrm{Zn (s) + Ag^+ (aq) \rightarrow Ag(s) + Zn^{2+}(aq)}\)
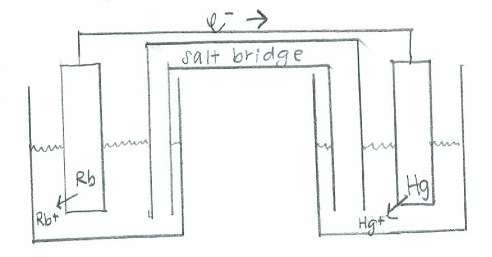
2. \(\mathrm{Rb(s) + Hg^{2+}(aq) \rightarrow Rb^+(aq) + Hg (s)}\)
3. \(\mathrm{F_2(g) + H_2O(l) \rightarrow 4F^-(aq) + O_2 (g) + H^+ (aq)}\)
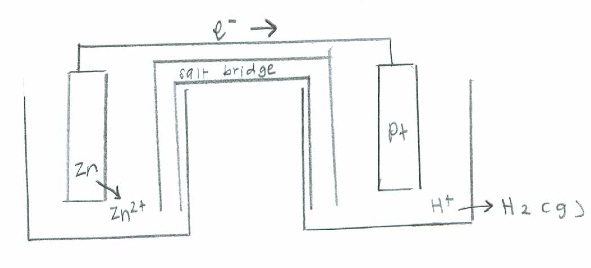
4. \(\mathrm{Zn (s) + H^+ (aq) \rightarrow Zn^{2+} (aq) + H_2 (g)}\)

S19.22A

1. Oxidation: \(\mathrm{Zn(s) \rightarrow Zn^{2+} (aq) + 2e^- \hspace{38.5 pt}\quad {E}^\circ=0.763\:V}\)

Reduction: \(\mathrm{(e^- + Ag^+(aq) \rightarrow Ag (s))\times2 \hspace{24 pt}\quad E^\circ=0.337\:V}\)

Net: \(\mathrm{Zn (s) + 2Ag^+ (aq) \rightarrow 2Ag(s) + Zn^{2+}(aq) \quad E^\circ_{cell}=1.100\:V}\)

2. Oxidation: \(\mathrm{(Rb(s) \rightarrow Rb^+(aq) + e^-)\times 2 \hspace{22 pt}\quad {E}^\circ=+2.93\:V}\)

Reduction: \(\mathrm{Hg^{2+}(aq) + 2e^- \rightarrow Hg (s) \hspace{43 pt}\quad E^\circ=0.86\:V}\)

Net: \(\mathrm{2Rb(s) + Hg^{2+}(aq)\rightarrow 2Rb^+(aq) + Hg (s) \quad E^\circ_{cell}=3.79\:V}\)

3. Oxidation: \(\mathrm{2H_2O (l) \rightarrow O_2(g) + 4H^+(aq) + 4e^- \hspace{31 pt} \quad {E}^\circ=-1.229\:V}\)

Reduction: \(\mathrm{(2e^-+F_2(g) \rightarrow 2F^-(aq))\times2 \hspace{60 pt} \quad E^\circ=2.866\:V}\)

Net: \(\mathrm{2F_2(g) + 2H_2O(l) \rightarrow 4F^-(aq) + O_2 (g) + 4H^+ (aq) \quad E^\circ_{cell}=1.637\:V}\)

4. Oxidation: \(\mathrm{Zn(s)\rightarrow Zn^{2+}(aq) + 2e^- \hspace{24 pt}\quad {E}^\circ=+0.76\:V }\)

Reduction: \(\mathrm{2H^+(aq)+ 2e^-\rightarrow H_2 (g) \hspace{26.5 pt} \quad E^\circ=0}\)

Net: \(\mathrm{Zn (s) + H^+ (aq) \rightarrow Zn^{2+} (aq) + H_2 (g) \quad E^\circ_{cell}=0.76\:V}\)

Q19.22B

Sketch a voltaic cell. Label anode and cathode. Indicate direction of electron flow, write balanced equation for reaction and calculate \(\mathrm{E^\circ_{cell}}\).

1. \(\ce{Fe^2+(aq)}\) displaced from solution by \(\ce{Li(s)}\)
2. \(\mathrm{Sn(s) + H^+(aq) + NO_3^-(aq) \rightarrow Sn^{2+}(aq) + H_2O(l) + NO(g) }\)
3. \(\mathrm{F_2(g) + H_2O(l) \rightarrow F^-(aq) + O_2(g) + H^+(aq)}\)
4. \(\mathrm{Cu(s) + F_2(g)\rightarrow Cu^{2+}(aq)+ 2F^- (aq)}\)

S19.22B

1. Anode = \(\ce{Li}\) electrode. Cathode = \(\ce{Fe}\) electrode

For voltaic cell, e^- flow from anode to cathode. Salt bridge connects the two solutions.

Anode: \(\mathrm{Li(s) \rightarrow Li^+(aq) + e^- \hspace{20 pt} \quad E^\circ_{cell} = -3.040\:V}\)

Cathode: \(\mathrm{Fe^{2+}(aq) + 2e^- \rightarrow Fe(s)\quad E^\circ_{cell} = -0.440\:V}\)

\(\mathrm{E^\circ_{cell} = -0.440\:V - (-3.040\:V) =+2.60\:V}\)

Balanced equation: \(\mathrm{2Li(s) + Fe^{2+}(aq) \rightarrow Fe(s) + 2Li^+(aq) }\)

2. Anode = \(\ce{Sn}\) electrode. Cathode = \(\ce{Pt}\) electrode

For voltaic cell, e^- flow from anode to cathode. Salt bridge connects the two solutions.

Anode: \(\mathrm{Sn(s) \rightarrow Sn^{2+}(aq) + 2e^-\hspace{113 pt}\quad E^\circ_{cell} =+0.137\:V}\)

Cathode: \(\mathrm{NO_3^-(aq) + 4H^+(aq) + 3e^- \rightarrow NO(g) + 2H_2O(l) \quad E^\circ_{cell} = +0.956\:V}\)

\(\mathrm{E^\circ_{cell} = +0.956\:V - (+0.137\:V) =+0.819\:V}\)

Balanced equation: \(\mathrm{3Sn(s) + 2NO_3^-(aq) + 8H^+(aq) \rightarrow 3Sn^{2+}(aq) +2NO(g) + 4H_2O(l)}\)

Cell diagram: \(\mathrm{Sn(s)|Sn^{2+}(aq) || H^+(aq),NO_3^-(aq)|NO(g)|Pt(s)}\)

3. Anode = \(\ce{Pt}\) electrode. Cathode = \(\ce{Pt}\) electrode

For voltaic cell, e^- flow from anode to cathode. Salt bridge connects the two solutions.

Anode: \(\mathrm{2H_2O(l) \rightarrow O_2(g) + 4H^+(aq) + 4e^-\quad E^\circ_{cell} = +1.229\:V}\)

Cathode: \(\mathrm{F_2(g) + 2e^- \rightarrow 2F^-(aq) \hspace{42 pt}\quad E^\circ_{cell} = +2.866\:V}\)

\(\mathrm{E^\circ_{cell} = +2.866\:V - (+1.229\:V) =+1.637\:V}\)

Balanced equation: \(\mathrm{2F_2(g) + 2H_2O(l) \rightarrow 4F^-(aq) + O_2(g) + 4H^+(aq)}\)

4. Anode = \(\ce{Cu}\) electrode. Cathode = \(\ce{Pt}\) electrode

For voltaic cell, e^- flow from anode to cathode. Salt bridge connects the two solutions.

Anode: \(\mathrm{Cu(s) \rightarrow Cu^{2+}(aq) + 2e^-\quad E^\circ_{cell} = +0.340\:V}\)

Cathode: \(\mathrm{F_2(g) + 2e^- \rightarrow 2F^-(aq)\quad E^\circ_{cell} = +2.866\:V }\)

\(\mathrm{E^\circ_{cell} = +2.866\:V - (+0.340\:V) = +2.526\:V}\)

Balanced equation: \(\mathrm{Cu(s) + F_2(g) \rightarrow Cu^{2+}(aq) + 2F^-(aq)}\)

Q19.22C

Identify where each reaction will take place (on the cathode or anode), balance the equation if necessary, and calculate the \(\mathrm{E^\circ_{cell}}\).

1. \(\mathrm{Fe^{3+} (aq) + Ag(s) \rightarrow Fe^{2+}(aq) + Ag^+(aq)}\)
2. \(\mathrm{Cu^{2+}(aq) + Zn(s) \rightarrow Cu(s) + Zn^{2+}(aq)}\)
3. \(\mathrm{Cd(s) + Cu^{2+}(aq) \rightarrow Cd^{2+} + Cu(s)}\)
4. \(\mathrm{Fe^{2+}(aq) + Cl_2(g) \rightarrow Fe^{3+}(aq) + 2Cl^-(aq)}\)

S19.22C

1. Reduction: \(\mathrm{Fe^{3+} (aq) + e^- \rightarrow Fe^{2+}(aq)}\) at the cathode (reduction occurs at the cathode)

Oxidation: \(\mathrm{Ag(s) \rightarrow Ag^+(aq) + e^-}\) at the anode

The equation is already balanced.

\(\mathrm{E^{\circ}_{cell} = (0.771 - 0.800) = -0.029\;V}\)

2. Reduction: \(\mathrm{Cu^{2+}(aq) + 2e^- \rightarrow Cu(s)}\) at the cathode, where reduction occurs

Oxidation: \(\mathrm{Zn(s) \rightarrow Zn^{2+}(aq) + 2e^-}\) at the anode

Reaction is already balanced

\(\mathrm{E^{\circ}_{cell} = 0.340 - (-0.763) = 1.103\;V}\)

3. Reduction: \(\mathrm{Cu^{2+}(aq) +2e^- \rightarrow Cu(s)}\) at the cathode, where reduction occurs

Oxidation: \(\mathrm{Cd(s) \rightarrow Cd^{2+} + 2e^-}\) at the anode

Reaction is already balanced

\(\mathrm{E^{\circ}_{cell}= E^{\circ}_{(right)} - E^{\circ}_{(left)} = 0.340 - 0.743 = -0.403}\)

4. Balance the equation, multiplying the iron half equation by 2 to equal the electrons

Reduction: \(\mathrm{Cl_2(g) + 2e^- \rightarrow 2Cl^-(aq)}\) at the cathode

Oxidation: \(\mathrm{2(Fe^{2+}(aq) \rightarrow 2Fe^{3+}(aq) +e^-)}\) at the anode

\(\mathrm{E^{\circ}_{cell} = 1.358 - (-0.440) = 1.798\;V}\)

For review on this topic, visit the page "Electrochemistry 2: Galvanic cells and electrodes".

Q19.25A

What are the \(\mathrm{\Delta G^\circ}\) for the reactions below?

1. \(\mathrm{Ti (s) + Cr^{2+}(aq) \rightarrow Ti^{2+}(aq) + Cr (s)}\)
2. \(\mathrm{2Cu^+(aq) + Sn^{4+} (aq) \rightarrow 2Cu^{2+}(aq) + Sn^{2+}(aq)}\)
3. \(\mathrm{2Cl_2(g) + 2H_2O(l) \rightarrow O_2(g) + 4H^+(aq) + 4Cl^-(aq)}\)

S19.25A

1. Oxidation: \(\mathrm{Ti(s)\rightarrow Ti^{2+}(aq) + 2e^- \hspace{29.5 pt}\quad {-E}^\circ=+1.63\:V}\)

Reduction: \(\mathrm{Cr^{2+}(aq) + 2e^- \rightarrow Cr (s) \hspace{30.5 pt}\quad E^\circ=-0.90\:V}\)

Net: \(\mathrm{Ti (s) + Cr^{2+}(aq) \rightarrow Ti^{2+}(aq) + Cr (s) \quad E^\circ_{cell}=0.73\:V}\)

\(\mathrm{\Delta G^\circ=-nF E^\circ_{cell}=-(2\: mole\: e^-)(96,485\: C/mol\: e^-)(0.73\:V)=-140,868.1\:J=-1.41\times10^2\:KJ}\)

2. Oxidation: \(\mathrm{Sn^{2+}(aq) \rightarrow 2e^- + Sn^{4+}(aq) \hspace{55 pt}\quad {-E}^\circ=-0.154\:V}\)

Reduction: \(\mathrm{(Cu^{2+}(aq) + e^- \rightarrow Cu^+(aq))\times2 \hspace{39 pt}\quad E^\circ=0.159\:V}\)

Net: \(\mathrm{2Cu^+(aq) + Sn^{4+} (aq) \rightarrow 2Cu^{2+}(aq) + Sn^{2+}(aq) \quad E^\circ_{cell}=0.005\:V}\)

\(\mathrm{\Delta G^\circ=-nFE^\circ_{cell}=-(2\: mole\: e^-)(96,485\: C/mol\: e^-)(0.005\:V)=-946.85\:J=-0.965\:KJ}\)

3. Oxidation: \(\mathrm{2H_2O(l) \rightarrow O_2(g) + 4H^+(aq) + 4e^- \hspace{39 pt}\quad {-E}^\circ=-1.229\:V}\)

Reduction: \(\mathrm{(Cl_2(g) + 2e^- \rightarrow 2 Cl^-(aq)) \times2 \hspace{60 pt}\quad E^\circ=1.358}\)

Net: \(\mathrm{2Cl_2(g) + 2H_2O(l) \rightarrow O_2(g) + 4H^+(aq) + 4Cl^-(aq) \quad E^\circ_{cell}=0.129\:V}\)

\(\mathrm{\Delta G^\circ=-nFE^\circ_{cell}=-(4\: mole\: e^-)(96,485\: C/mol\: e^-)(0.129\:V)= -49,786.26\: J= -4.98\times10^4\: KJ}\)

Q19.25B

Determine \(\mathrm{\Delta G^\circ}\) for reactions:

1. \(\mathrm{O_2(g) + 4H^+(aq) + 4Br^-(aq) \rightarrow 2H_2O(l) + 2Br_2(g)}\)
2. \(\mathrm{Cr_2O_7^{2-}(aq) + 14H^+(aq)+ 6K(s) \rightarrow 2Cr^{3+}(aq) + 6K^+(aq) + 7H_2O(l)}\)
3. \(\mathrm{Cu(s) + Br_2(l) \rightarrow Cu^{2+}(aq)+2Br^-(aq)}\)

S19.25B

\(\mathrm{\Delta G^\circ = -nFE^\circ_{cell}}\)

1. Oxidation: \(\mathrm{4Br^-(aq) \rightarrow 2Br_2(g) + 4e^- \hspace{39 pt}\quad E^\circ_{cell} =+1.065\:V}\)

Reduction: \(\mathrm{O_2(g) + 4e^- + 4H^+(aq)\rightarrow 2H_2O(l)\quad E^\circ_{cell} =+1.229\:V}\)

\(\mathrm{E^\circ_{cell} = +1.229\:V - +1.065\:V = 0.164\:V}\)

\(\mathrm{n = 4\;e^-}\)

\(\mathrm{F = 96,485\:C/mol\:e^-}\)

\(\mathrm{\Delta G^\circ = -(4 e^-)(96,485\:C/mol\:e^-)(0.164\:V) = - 63294.16\:J = - 63\:kJ }\)

2. Oxidation: \(\mathrm{6K(s)\rightarrow 6K^+(aq) +6e^- \hspace{134 pt}\quad E^\circ_{cell} =-2.924\:V}\)

Reduction: \(\mathrm{Cr_2O_7^{2-}(aq) + 6e^- + 14H^+(aq)\rightarrow 2Cr^{3+}(aq) + 7H_2O(l)\quad E^\circ_{cell} =+1.33\:V}\)

\(\mathrm{E^\circ_{cell} = +1.33\:V - (-2.924\:V) = 4.254\:V}\)

\(\mathrm{n = 6\:e^- }\)

\(\mathrm{F = 96,485\;C/mol\;e^-}\)

\(\mathrm{\Delta G^\circ = \dfrac{-(6\;e^-)(96,485\;C/mol\;e^-)(4.254\:V)}{1000} = -2462.68\:kJ}\)

3. Oxidation: \(\mathrm{Cu(s) \rightarrow Cu^{2+}(aq) + 2e^- \hspace{5.5 pt} \quad E^\circ_{cell} = +0.340\:V}\)

Reduction: \(\mathrm{Br_2(l) + 2e^- \rightarrow 2Br^-(aq)\quad E^\circ_{cell}= +1.065\:V}\)

\(\mathrm{E^\circ_{cell} = +1.065\:V - +0.340\:V = +0.725\:V}\)

\(\mathrm{n = 2\:e^-}\)

\(\mathrm{F = 96,485\:C/mol\:e^-}\)

\(\mathrm{\Delta G^\circ = -(2 e^-)(96,485\:C/mol\:e^-)(0.725\:V) = -139903 \:J = -139.9\:kJ}\)

Q19.25C

Find the values of \(\mathrm{\Delta G}\) for the following reactions in the voltaic cells

1. \(\mathrm{2V^{3+}(aq) + Ni(s) \rightarrow 2V^{2+}(aq) + Ni^{2+}(aq)}\)
2. \(\mathrm{2Al (s) +3Br_2(l) \rightarrow 2Al^{3+}(aq) + 6Br^-}\)
3. \(\mathrm{2Cu^{2+}(aq) + Sn^{2+} (aq) \rightarrow 2Cu + Sn^{4+}}\)

S19.25C

1. The \(\mathrm{z}\) (moles of electrons) \(\mathrm{= 2}\)

\(\begin{align} \mathrm{E^{\circ}_{cell}} & = \mathrm{E^{\circ}_{(reduction)}- E^{\circ}_{(oxidation)}} \\
& = \mathrm{-0.255 - (-0.257) = 0.002\;V} \end{align}\)

\(\mathrm{\Delta G = -zFE^{\circ}_{cell} = -{2 \: mol \: e}^- \times 96485 \: C \times 0.002 \: V=-385.94J}\)

2. The \(\mathrm{z}\) (moles of electrons) \(\mathrm{= 6}\)

\(\mathrm{E^{\circ}_{cell} = E^{\circ}_{(reduction)} - E^{\circ}_{(oxidation)} = 1.065 - (-1.676) = 2.741\;V}\)

\(\mathrm{\Delta G = -zFE^{\circ}_{cell} = -{6 \: mol \: e}^- \times 96485 \: C \times 2.741 \: V=-1.59 \times 10^6J}\)

3. The \(\mathrm{z}\) (moles of electrons transferred) \(\mathrm{= 2}\)

\(\mathrm{E^{\circ}_{cell}=0.337- 0.150 = 0.187\;V}\)

\(\mathrm{\Delta G = -zFE^{\circ}_{cell} = -{2 \: mol \: e}^- \times 96485 \: C \times 0.187 \: V=-3.61 \times 10^4 J}\)

Q19.27A

Find \(\mathrm{E^\circ}\), \(\mathrm{\Delta G^\circ}\), \(\ce{K}\), and given that the reactants and products are in their standard state, if they go to completion or not for the following reaction:

\(\mathrm{2BrO_3^-(aq) + 12H^+(aq) + 10SO_4^{2-}(aq) \rightarrow 5S_2O_8^{2-}(aq) + Br_2(l) + 6H_2O (l)}\)

S19.27A

Oxidation: \(\mathrm{(2SO_4^{2-}(aq) \rightarrow S_2O_8^{2-}(aq) + 2e^-)\times5 \hspace{127 pt}\quad {-E}^\circ=-2.01\:V}\)

Reduction: \(\mathrm{2BrO_3^-(aq) + 12H^+(aq) +10e^- \rightarrow Br_2(l) + 6H_2O (l) \hspace{67 pt}\quad E^\circ=1.478\:V}\)

Net: \(\mathrm{2BrO_3^-(aq) + 12H^+(aq) + 10SO_4^{2-}(aq) \rightarrow5S_2O_8^{2-}(aq) + Br_2(l) + 6H_2O (l) \quad E^\circ_{cell}=-0.532\:V}\)

\(\mathrm{\Delta G^\circ=-nFE^\circ_{cell}=-(10\: mole\: e^-)(96,485\: C/mol\: e^-)(-0.532\:V)=5.13\times10^2\:KJ/mol}\)

\(\mathrm{\Delta G^\circ=-RT\ln K}\)

\(\mathrm{5.13\times10^2\:KJ/mol = -(-8.314\:KJ/mol)(298.15\:K)\ln K}\)

\(\mathrm{K=8.13\times10^{-1}}\)

Since \(\ce{K}\) is small (\(\mathrm{<1}\)) the reaction will not go to completion.

Q19.27B

Find \(\mathrm{E^\circ_{cell}}\), \(\mathrm{\Delta G^\circ}\), \(\ce{K}\), and whether reaction goes to completion at 298 K and all substances at standard states for: \(\mathrm{3HClO_2(aq) + 2Cr^{3+}(aq) + 12H_2O(l)\rightarrow 3HClO(aq) + Cr_2O_7^{2-}(aq) + 8H_3O^+(aq)}\)

S19.27B

Note:

\(\mathrm{\Delta G^\circ =-nFE^\circ_{cell} }\)

\(\mathrm{\ln K_{eq} = - \dfrac{\Delta G^\circ}{RT}}\)

Large \(\mathrm{K_{eq}}\) = reaction goes to completion

Oxidation: \(\mathrm{2Cr^{3+}(aq)+ 21H_2O(l) \rightarrow Cr_2O_7^{2-}(aq) + 14H_3O^+(aq) + 6e^- \quad E^\circ_{cell} = +1.33\:V}\)
Reduction: \(\mathrm{3HClO_2(aq) + 6H_3O^+(aq) + 6e^- \rightarrow 3HClO(aq) + 9H_2O(l) \hspace{1 pt}\quad E^\circ_{cell} = +1.64\:V}\) \(\mathrm{E^\circ_{cell} = +1.64\:V - +1.33\:V =+0.31\:V}\) \(\mathrm{\Delta G^\circ = \dfrac{-(6e^-)(96,485\:C/mol\:e^-)(0.31\:V)}{1000} = -179.46\:kJ}\) \(\mathrm{\ln K_{eq} = - \dfrac{-179.46\:kJ \times 1000}{(8.3145\:J\:K^{-1}mol^{-1})(298\:K)} = 72.4}\) \(\mathrm{K = 2.86 \times 10^{31}}\) Thus since \(\ce{K}\) is very large, reaction will go to completion.

Q19.27C

In the reaction given, calculate the a) \(\mathrm{E^\circ_{cell}}\) b) \(\mathrm{\Delta G}\) c) \(\mathrm{K}\) d) and if the reaction goes towards completion when the reactants and products are in their standard states:

\(\mathrm{O_2(g) + 4I^-(aq) + 4H^+(aq) \rightarrow 2H_2O (l) +2I_2(s)}\)

S19.27C

1. \(\mathrm{E^{\circ}_{cell} = reduction - oxidation}\)

\(\hspace{20 pt}= (1.229) - (0.535)\)

\(\hspace{20 pt}= \mathrm{0.694\;V}\)

2. \(\begin{align} \mathrm{\Delta G} & = \mathrm{-zF E^{\circ}_{cell}= -\dfrac{\textrm{4 mol e}^- \times (\textrm{96485 C})}{\textrm{1 mol e}^- \times \textrm{0.694 V}}} \\ & = \mathrm{-267842\;J} \end{align}\)
3. \(\mathrm{E^\circ_{cell} = \dfrac{0.025693\;V}{z}\ln (K)}\)

\(\mathrm{0.694\;V = \dfrac{0.025693\;V}{4}\ln (K)}\)

\(\mathrm K = 8.38 \times 10^{46}\)

4. Since k is very large, the reaction will go substantially towards completion at standard states.

For review on this topic, visit the page "Electrochemistry 3: Cell potentials and thermodynamics".

Q19.31A

Calculate the theoretical cell voltage for the reaction between copper and zinc given that the overall reaction is:
\(\mathrm{Zn(s) + Cu^{2+}(aq) \rightarrow Zn^{2+}(aq) + Cu(s)}\)

S19.31A

Oxidation: \(\mathrm{Zn(s) \rightarrow Zn^{2+}(aq) + 2e^- \quad E^\circ= -(-0.763\: V)}\)
Reduction: \(\mathrm{Cu^{2+}(aq) + 2e^- \rightarrow Cu(s) \hspace{1 pt}\quad E^\circ= 0.340\: V}\)
\(\mathrm{E^\circ_{cell}= 0.763\:V + 0.340\:V = +1.103\:V}\)

Q19.31B

Calculate a theoretical voltage of silver-lead button cell at 298K. Cell reaction: \(\mathrm{Pb(s) + Ag_2O(s) \rightarrow PbO(s) + 2Ag(s) }\) \(\mathrm{\Delta G_f^\circ}\) for \(\mathrm{PbO(s) = -187.9\: kJ/mol}\) \(\mathrm{\Delta G_f^\circ}\) for \(\mathrm{Ag_2O(s) = -11.20\: kJ/mol}\) \(\mathrm{\Delta G_f^\circ}\) for \(\mathrm{2Ag(s) = 0\: kJ/mol}\) \(\mathrm{\Delta G_f^\circ}\) for \(\mathrm{Pb(s) = 0\: kJ/mol}\)

S19.31B

\(\mathrm{\Delta G^\circ = \Delta G_f^\circ[PbO(s)] + 2\Delta G_f^\circ[Ag(s)] - \Delta G_f^\circ[Pb(s)] - \Delta G_f^\circ[Ag_2O(s)]}\) \(\begin{align} \mathrm{\Delta \textrm{G of PbO(s)}} &= \mathrm{-187.9\:kJ/mol + 2(0) - 0 - (-11.20\:kJ/mol)} \\
&= \mathrm{-176.7 kJ/mol}\end{align}\) Use \(\mathrm{\Delta G^\circ =-nFE^\circ_{cell}}\) to find \(\mathrm{E^\circ_{cell}}\). \(\mathrm{E^\circ_{cell} = - \dfrac{\Delta G^\circ}{nF} = - \dfrac{(-176.7\:kJ/mol \times 1000)}{(2e^-)(96,485\:C/mol\:e^-)} = 0.9157\:V}\)

Q19.31C

From the information in appendix D, calculate the theoretical voltage for the hydrogen fuel cell reaction depicted below, and calculate the \(\mathrm{E^\circ_{cell}}\):

\(\mathrm {2H_2(g) + O_2(g) \rightarrow 2H_2O (l) }\)

S19.31C

\(\mathrm{2 \times \Delta G(H_2O) - [\Delta G(O_2) + 2\Delta G(H_2)]}\)

\(=\mathrm{2(-237.1\: KJ) - 0 + 2(0)\:KJ}\) (numbers found from appendix D in the textbook)

\(\Delta \mathrm G = -474.2 - 0\)

\(\Delta \mathrm G = -474.2\)

Then, use \(\mathrm{\Delta G}\) to calculate \(\mathrm{E^\circ_{cell}}\)

\(\mathrm{-474.2= -zF E^{\circ}_{cell} = -(2\:mol\:e^- \times \dfrac{96485\:C} {1\:mol\:e^-} \times E^{\circ}_{cell})}\)

\(\mathrm{E^{\circ}_{cell} = 0.0025\:V}\)

Q19.35A

A voltaic cell has an \(\mathrm{E_{cell}}\) value of 1.536 V. What is the concentration of \(\ce{Ag+}\) in the cell?

\(\mathrm{Zn(s) | Zn^{2+}(2.00\:M) || Ag^+(x\:M) | Ag(s)}\)

S19.35A

First, determine \(\mathrm{E^\circ_{cell}}\):
Oxidation: \(\mathrm{Zn(s) \rightarrow Zn^{2+}(aq) + 2e^- \hspace{77 pt}\quad -E^\circ= 0.763\: V}\)
Reduction: \(\mathrm{2Ag^+(aq) + 2e^- \rightarrow Ag(s) \hspace{70 pt}\quad E^\circ= 0.800\: V}\)
Net Reaction: \(\mathrm{Zn(s) + 2Ag^+(aq) \rightarrow Zn^{2+}(aq) + Ag(s) \quad E^\circ_{cell}= 1.563\: V}\)

Second, use Nernst equation to calculate \(\ce{[Ag+]}\)
\(\mathrm{E=E^\circ_{cell}-\dfrac{0.0592}{n}\log\dfrac{[Zn^{2+}]}{[Ag^+]^2}}\)
\(\mathrm{1.536=1.563-\dfrac{0.0592}{2}\log\dfrac{2}{x^2}}\)
\(\mathrm{-0.027\left (\dfrac{-2}{0.0592} \right )=log\dfrac{2}{x^2}}\)
\(\mathrm{8.168=\dfrac{2}{x^2}}\)
\(\mathrm{x^2=0.2448}\)
\(\mathrm{x=0.495=[Ag^+]}\)

Q19.35B

Find \(\ce{[H2O2(aq)]}\) in cell if the voltaic cell's \(\mathrm{E_{cell} = 1.500\:V}\). \(\mathrm{Zn(s)|Zn^{2+}(aq) (1.00\:M) || H_2O_2(aq)(x M) | H_2O(l)}\) Hint: use Nernst's Equation.

S19.35B

Anode: \(\mathrm{Zn(s) \rightarrow Zn^{2+}(aq) + 2e^- \hspace{68 pt}\quad E^\circ_{cell} = -0.763\:V}\)

Cathode: \(\mathrm{H_2O_2(aq) + 2H^+(aq) + 2e^- \rightarrow 2H_2O(l) \quad E^\circ_{cell} = +1.763\:V}\)

\(\mathrm{E^\circ_{cell} = +1.763\:V - (-0.763\:V) = 2.526\:V}\) \(\mathrm{E = E^\circ_{cell} - \dfrac{0.0592}{n} \log \dfrac{[Zn^{2+}]}{[H_2O_2]}}\) \(\mathrm{1.5\:V = 2.526\:V - \dfrac{0.0592}{2}\log\dfrac{1}{x}}\)

\(\mathrm{x = 2.18 \times 10^{-35}\:M}\)

\(\mathrm{[H_2O_2(aq)] = 2.18 \times 10^{-35}\:M}\)

Q19.35C

The voltaic cell in the following diagram has an \(\mathrm{E^\circ_{cell}= 0.5464\: V}\). Solve for the \(\mathrm{[Cl^-]}\) in the cell

\(\mathrm{Ag (s)|Ag^+(0.40\:M)||Cl^- (x\:M),\,Cl_2 (0.60\:atm)|Pt(s)}\)

S19.35C

First calculate \(\mathrm{E^\circ_{cell}}\), the theoretical potential. This value is 0.558 V. Then plug in given values to the Nernst formula

\(\mathrm{E_{cell} = E^{\circ}_{cell}-\dfrac{0.0592}{n}\times \log Q}\)

Plugging in values gives us

\(0.5465 = 0.558 - \dfrac{0.0592}{6}\times \log \dfrac{(0.40^2)(x^2)}{0.60}\)

Using algebra to isolate the variable on one side, we find that \(\mathrm{[Cl^-] = 0.50 }\).

For review on this topic, visit the page "Electrochemistry 4: The Nernst Equation".

Q19.37A

Using the Nernst equation, find \(\mathrm{E_{cell}}\) for the following cells:

1. \(\mathrm{Al(s) | Al^{3+}(0.30\:M) || Fe^{2+}(1.1\:M) | Fe(s)}\)
2. \(\mathrm{Co(s) | Co^{2+}(0.6\:M) || Fe^{3+}(1.0\:M), Fe^{2+}(0.9\:M) | Pt(s)}\)

S19.37A

1. First, determine \(\mathrm{E^\circ_{cell}}\)

Oxidation: \(\mathrm{2Al(s) \rightarrow 2Al^{3+}(aq) + 6e^- \hspace{115 pt} \quad -E^\circ_{cell}= 1.676\: V}\)
Reduction: \(\mathrm{3Fe^{2+}(aq) + 6e^- \rightarrow 3Fe(s) \hspace{110 pt} \quad E^\circ_{cell}= -0.440\: V}\)
Net Reaction: \(\mathrm{2Al(s) + 3Fe^{2+}(1.1\:M) \rightarrow 2Al^{3+}(0.30\:M) + 3Fe(s) \quad E^\circ_{cell}= 1.236\: V}\)

Second, use Nernst equation to calculate \(\mathrm{E_{cell}}\)
\(\mathrm{E_{cell}=E^\circ_{cell}-\dfrac{0.0592}{n}\log\dfrac{[Al^{3+}]^2}{[Fe^{2+}]^3}}\)
\(\mathrm{E_{cell}=1.236-\dfrac{0.0592}{6}\log\dfrac{(0.3)^2}{(1.1)^3}}\)
\(\mathrm{E_{cell}=1.248}\)

2. First, determine \(\mathrm{E^\circ_{cell}}\)

Oxidation: \(\mathrm{Co(s) \rightarrow Co^{2+}(aq) + 2e^- \hspace{131 pt}\quad {-E}^\circ_{cell}=0.277\: V}\)
Reduction: \(\mathrm{2Fe^{3+}(aq) + 2e^- \rightarrow 2Fe^{2+}(aq) \hspace{112 pt}\quad E^\circ_{cell}=0.771}\)
Net Reaction: \(\mathrm{Co(s) + 2Fe^{3+}(1.0\:M) \rightarrow Co^{2+}(0.6\:M) +2Fe^{2+}(0.9\:M) \quad E^\circ_{cell}=1.048\: V}\)

Second, use Nernst equation to calculate \(\mathrm{E_{cell}}\)
\(\mathrm{E_{cell}=E^\circ_{cell}-\dfrac{0.0592}{n}\log\dfrac{[Fe^{2+}]^2[Co^{2+}]}{[Fe^{3+}]^2}}\)
\(\mathrm{E_{cell}=1.048-\dfrac{0.0592}{2}\log\dfrac{(0.9)^2(0.6)}{(1.0)^2}}\)
\(\mathrm{E_{cell}=1.057\: V}\)

Q19.37B

Use Nernst's Equation to calculate \(\mathrm{E_{cell}}\) for:

1. \(\mathrm{Al(s) | Al^{3+}(aq) (0.20\:M) || Sn^{2+}(aq)(0.90\:M)| Sn(s)}\)
2. \(\mathrm{Zn(s) | Zn^{2+}(aq) (0.42\:M) || Cl^- (0.02\:M), Cl_2 (g,\: 0.5\: atm) | Pt(s) }\)

S19.37B

Calculate \(\mathrm{E^\circ_{cell}}\), then use Nernst equation to calculate \(\mathrm{E_{cell}}\)

1. Oxidation: \(\mathrm{Al(s) \rightarrow Al^{3+}(aq) (0.20\:M) + 3e^- \quad E^\circ_{cell} = -1.676\:V}\)

Reduction: \(\mathrm{Sn^{2+}(aq) (0.90\:M) + 2e^- \rightarrow Sn(s) \quad E^\circ_{cell} = -0.137\:V}\)

\(\mathrm{E^\circ_{cell} = -0.137\:V -(-1.676\:V) = 1.539\:V}\)

\(\mathrm{E_{cell} = E^\circ_{cell} - \dfrac{0.0592}{n} \log \dfrac{[Al^{3+}]^2}{[Sn^{2+}]^3}}\)

\(\mathrm{E_{cell} = 1.539\: V - \dfrac{0.0592}{6} \log \dfrac{(0.20\:M)^2}{(0.90\:M)^3}}\)

\(\mathrm{E_{cell} = 1.551\: V}\)

2. Oxidation: \(\mathrm{Zn(s) \rightarrow Zn^{2+}(aq) (0.42\:M) + 2e^- \hspace{33 pt} \quad E^\circ_{cell} = -0.763\:V}\)

Reduction: \(\mathrm{Cl_2 (g,\: 0.5\: atm) + 2e^- \rightarrow 2Cl^- (0.02\:M)\quad E^\circ_{cell} = +1.358\:V}\)

\(\mathrm{E^\circ_{cell} = +1.358\:V - (-0.763\:V) = 2.121\:V}\)

\(\mathrm{E_{cell} = E^\circ_{cell} - \dfrac{0.0592}{n} \log \dfrac{[Zn^{2+}][Cl^-]^2}{P_{Cl_2(g)} }}\)

\(\mathrm{E_{cell} = 2.121\:V - \dfrac{0.0592}{2} \log \dfrac{[0.42\:M][0.02\:M]^2}{0.5\:atm}}\)

\(\mathrm{E_{cell} = 2.223\:V}\)

Q19.37C

Using the Nernst equation and a list of \(\mathrm{E^\circ_{cell}}\) values, calculate the \(\mathrm{E_{cell}}\) for the following cells:

1. \(\mathrm{Al(s)| Al^{3+}(0.36\:M)||Sn^{4+}(0.086\:M),\,Sn^{2+}(0.54\:M)|Pt}\)
2. \(\mathrm{Sn(s)|Sn^{2+}(0.01\:M)||Pb^{2+}(0.700\:M)|Pb(s)}\)

S19.37C

1. \(\mathrm{E^{\circ}_{cell} = 0.154 - (-1.676) = 1.83}\)

Using the Nernst equation \(\mathrm{E_{cell} = E^{\circ}_{cell}-\dfrac{0.0592}{n}\times\log Q}\), we simply need to set up the \(\mathrm{Q}\) and establish that our \(\mathrm{n}\) (moles of electrons transferred) is 2.

Thus, the \(\mathrm{Q} = \dfrac{(0.54)(0.36)^2}{(0.086)}\) and plugging in the found \(\mathrm{E^\circ_{cell}}\) gives us an \(\mathrm{E_{cell}}\) value of 1.827 V

2. \(\mathrm{E^{\circ}_{cell} = -0.125 - (-0.137) = 0.012\:V}\)

Using the Nernst equation \(\mathrm{E_{cell} = E^{\circ}_{cell} - \dfrac{0.0592}{n}\times \log Q}\), we now need to establish our \(\mathrm{Q}\). The overall equation would be \(\mathrm{Pb^{2+}(aq) + Sn(s) \rightarrow Sn^{2+}(aq) + Pb(s)}\)

Thus, the \(\mathrm{Q}\) would be \(\dfrac{0.01}{0.700}\) and the \(\mathrm{E_{cell}}\) calculates out to 0.067V

For review on this topic, visit the page "Electrochemistry 4: The Nernst Equation".

Q19.41A

If \(\ce{[Cu^2+]}\) is maintained at 1.0 M, what is the minimum \(\ce{[Ag+]}\) for which the reaction from 19.2, given below, is spontaneous in the forward direction?

\[\mathrm{Cu(s) + 2Ag^+(aq) \rightarrow Cu^{2+}(aq) + 2Ag(s)}\]

S19.41A

Remember - in order for the reaction to be spontaneous, \(\mathrm{\Delta G<0}\).

Important equations:

\(\mathrm{E^\circ_{cell} = E^\circ_{cathode} - E^\circ_{anode}}\)
\(\mathrm{0 = E^\circ - \dfrac{RT}{nF}\ln Q \:\Rightarrow \: E^\circ= \dfrac{RT}{nF}\ln Q}\)
\(\mathrm{Q = \frac{[Cu^{2+}]}{ [Ag^+]^2}}\)

Write the equation as a cell diagram:

\(\mathrm{Cu(s) | Cu^{2+}(aq) || Ag^+(aq) | Ag(s)}\)
Oxidation: \(\mathrm{Cu(s) \rightarrow Cu^{2+}(aq) + 2e^- \hspace{19 pt}\quad E^\circ= -0.340}\)
Reduction: \(\mathrm{(Ag^+(aq) + e^- \rightarrow Ag(s))\times2 \quad E^\circ= 0.800}\)
Net reaction: \(\mathrm{Cu(s) + 2Ag^+(aq) \rightarrow Cu^{2+}(aq) + 2Ag(s)}\)
\(\mathrm{E^\circ_{cell} = 0.800 - 0.340 = 0.46\:V}\)
\(\mathrm{0.46 = \dfrac{RT}{2F}\ln\dfrac{[1]}{[Ag^+]^2}}\)
\(\mathrm{0.46 = \dfrac{RT}{2F}(\ln1-\ln[Ag^+]^2)}\)
\(\mathrm{0.46 = -\dfrac{RT}{2F}\ln[Ag^+]^2}\)
\(\mathrm{0.46 = -\dfrac{(8.3145)(298)}{2(96485)}\ln[Ag^+]^2}\)
Solve for \(\ce{[Ag^+]}\)
\(\mathrm{[Ag^+] = 1.66\times10^{-8}\: M}\)

Q19.41B

When \(\ce{[Pb^2+]}\) is maintained at 1.1 M for reaction:

\(\mathrm{Pb(s) + Cu^{2+}(aq)\rightarrow Cu(s) + Pb^{2+}(aq)}\)

1. What is the minimum \(\ce{[Cu^2+]}\) for reaction to be spontaneous in forward direction?
2. Will the displacement of \(\ce{Cu^2+(aq)}\) by \(\ce{Pb(s)}\) go to completion? Explain reasoning.

S19.41B

Oxidation: \(\mathrm{Pb(s) \rightarrow Pb^{2+}(aq) + 2e^- \hspace{4 pt} \quad E^\circ_{cell} = -0.125\:V}\) Reduction: \(\mathrm{Cu^{2+}(aq) + 2e^- \rightarrow Cu(s) \quad E^\circ_{cell} = +0.340\:V}\) \(\mathrm{E^\circ_{cell} = +0.340\:V - (-0.125\:V) = 0.465\: V}\)

1. Minimum [Cu²⁺] for spontaneous \(\mathrm{=E_{cell} =0\: V}\) (positive \(\mathrm{E_{cell}}\))

\(\mathrm{E_{cell} = E^\circ_{cell} -\dfrac{0.0592}{n} \log \dfrac{[Pb^{2+}(aq)]}{[Cu^{2+}(aq)]}}\)

\(\mathrm{0\:V = 0.465\:V - \dfrac{0.0592}{2}\log\dfrac{[1.1 M]}{x}}\)

\(\mathrm{x = 2.15 \times 10^{-16}\,M}\)

Minimum [Cu²⁺_(aq)] for spontaneous reaction \(\mathrm{= 2.15 \times 10^{-16}\, M}\)

2. Work the problem backwards,

Assume: \(\mathrm{[Cu^{2+}]_{initial} = 1.1\:M}\) and \(\mathrm{[Pb^{2+}]_{initial} = 0.0\:M}\),

then: \(\mathrm{[Cu^{2+}]_{final} = 2.15 \times 10^{-16}\: M}\) and \(\mathrm{[Pb^{2+}]_{final} = 1.1\:M}\).

Thus, reaction will go to completion.

Q19.41C

If \(\ce{[Cu^2+]}\) is maintained at 2.0 M

What is the minimum \(\ce{[Ag+]}\) must be at to push the forward direction spontaneously. Use equation \(\mathrm{Cu(s) + 2Ag^+(aq) \rightarrow Cu^{2+}(aq) + 2Ag(s)}\).

S19.41C

To push a reaction forward spontaneously, the \(\mathrm{E_{cell}}\) must be greater than 0. We find the \(\mathrm{E^\circ_{cell}}\) = 0.460 V.

Next, plug in the values given to the Nernst equation. The number of moles of electrons being transferred is 2. The equation will be set up as:

\(0 > 0.460 - \dfrac{0.0592}{2} \times \log\dfrac{2}{x^2}\)

Remember to account for coefficients in setting up the \(\mathrm{Q}\). Now solve for x \(\ce{[Ag+]}\) and we find that \(\mathrm{x = 2.4 \times 10^{-8}\, M}\).

For review on this topic, visit the page "Electrochemistry 4: The Nernst Equation".

Q19.45A

Solve for \(\mathrm{E_{cell}}\) of the following voltaic cell

\(\mathrm{Cu(s) | Cu^{2+} (0.01\:M) || Cu^{2+} (0.1\:M) | Cu(s)}\)

S19.45A

First solve for \(\mathrm{E^\circ_{cell}}\)

Oxidation: \(\mathrm{Cu(s) \rightarrow Cu^{2+} + 2e^- \quad E^\circ = -0.340}\)

Reduction: \(\mathrm{Cu^{2+}(aq) + 2e^- \rightarrow Cu(s) \quad E^\circ= +0.340}\)

\(\mathrm{E^\circ_{cell} = E^\circ_{cathode} - E^\circ_{anode}}\)

\(\mathrm{0.340-0.340 = 0}\)

Then use the Nernst Equation to solve for \(\mathrm{E_{cell}}\)

\(\begin{align}
\mathrm{E_{cell}} & = \mathrm{E^\circ_{cell} - \dfrac{0.0257}{2}\ln Q} \\
& = \mathrm{0 - \dfrac{0.0257}{2}\ln\dfrac{0.01\:M}{0.1\:M}} \\
\mathrm{E_{cell}} & = \mathrm{0.0296\:V}
\end{align}\)

Q19.45B

Voltaic cell: What is the value of \(\mathrm{E_{cell}}\) when \(\mathrm{K_{sp}}\) of \(\mathrm{Na_2CrO_4 = 1.3 \times 10^{-12}}\)? \(\mathrm{Na(s) | Na^+(aq) (satd\: Na_2CrO_4)|| Na^+ (0.130\:M) | Na(s)}\)

S19.45B

Find \(\ce{[Na+(aq)]}\) in saturated solution of \(\ce{Na2CrO4}\) \(\mathrm{K_{sp} =[Na^+]^2[CrO_4^{2-}] = (2s)^2(s) = 4s^3 = 1.3 \times 10^{-12}}\) \(\mathrm{s = 6.9 \times 10^{-5}\, M}\) Concentration cell \(\mathrm{= E^\circ_{cell} = 0\: V}\) and \(\mathrm{n = 1}\), \(\mathrm{[Na^+]_{anode} = 2s = 1.38 \times 10^{-4}\: M}\) Cell reaction: \(\mathrm{Na(s) + Na^+ (0.130\:M) \times Na(s) + Na^+(aq) (1.38 \times 10^{-4}\: M)}\) \(\mathrm{E_{cell} = E^\circ_{cell} - \dfrac{0.0592}{n}\log \dfrac{[Na^+(satd\: Na_2CrO_4)]}{[Na^+]}}\) \(\mathrm{E_{cell} = 0\:V - \dfrac{0.0592}{1}\log \dfrac{1.38 \times 10^{-4}\:M}{0.130\: M}}\) \(\mathrm{E_{cell} = 0.176\:V}\)

Q19.45C

The following voltaic cell is constructed:

\(\mathrm{Pb(s)||Pb^{2+}(satd\:PbI_2)||Pb^{2+}(0.100\:M)|Pb(s)}\). Given that the \(\mathrm{E_{cell} = 0.0567\: V}\), find the \(\mathrm{K_{sp}}\).

S19.45C

Set up the Nernst equation with the values appropriate for this equation. The moles of electrons transferred are 2. The \(\mathrm{E^\circ_{cell}}\) for this would be 0.

Thus, the Nernst equation sets up as \(\mathrm{0.0567 = E^{\circ}_{cell} - \dfrac{0.0592}{n}\times \log Q}\)

\(\mathrm{0.0567 = E^{\circ}_{cell} - \dfrac{0.0592}{n}\times \log \dfrac{x}{0.100}}\)

Solve for the value of x algebraically; this will yield an X value of 0.001215.

This value is not the answer; it is how much \(\ce{Pb^2+}\) needs to be saturated in the equation. To find the \(\mathrm{K_{sp}}\), note the stoichiometric values for \(\ce{[Pb]}\) and \(\mathrm{[I^-]^2}\). The \(\ce{Pb}\) and \(\ce{I}\) concentrations have been found. Now plug in your x value and \(\mathrm{K_{sp} = [Pb][I^-]^2}\)and \(\mathrm{K_{sp} =1.79 \times 10^{-9}}\).

For review on this topic, visit the page "Electrochemistry 4: The Nernst Equation".

Q19.59A

By referring back to figure 19-20, explain what would happen at each individual circumstance

1. zinc is wrapped around the head and tip of the iron nail
2. a hole is poked at the center of an iron nail
3. the nail is completely covered with copper

S19.59A

1. Through cathodic protection, zinc would get oxidized first. The zinc would protect the nail from oxidation.
2. Oxidation would occur even more because there would now be another head and tip. With more strained regions, the air would be able to oxidize the nail more.
3. The entire nail will be oxidized since copper isn't a sacrificial anode. It won't protect it from corrosion.

Q19.59B

What would happen to the corrosion of iron nail under phenolphtalein indicator, if:

1. Lead wire are wrapped around the nail
2. Deep scratch occurred at the iron nail
3. Galvanized nail is substituted for the iron nail

S19.59B

1. Weaker reducing agent (lower tendency to get oxidized) = less reactive metal. Since lead, \(\ce{Pb}\), is a weaker reducing agent than iron, oxidation of \(\ce{Fe(s)}\) would be enhanced into \(\ce{Fe^2+(aq)}\) - blue precipitate occurs. \(\ce{OH- (aq)}\) would be produced near the lead wire - pink color occurs (electron lost in oxidation).
2. Scratch exposes the metal, more susceptible to corrosion. Blue precipitate around the scratch should occur.
3. Zinc protect iron from corrosion as it is a stronger reducing agent (better tendency to be oxidized). Thus there should be no blue precipitate. Zinc corrodes instead. Pink color of \(\ce{OH- (aq)}\) would still continue to form.

Q19.59C

Imagine an iron nail that is corroding in a solution. Predict the appearance of the nail under the given conditions using your knowledge of corrosion in voltaic cells. Assume standard temperature conditions.

1. The head and tip of the nail are covered in magnesium.
2. The nail is galvanized, but there is a break in plating.
3. The nail is plated in copper, but there is a break in plating.

S19.59C

1. Magnesium is a sacrificial anode, meaning it is extremely willing to be oxidized. The \(\mathrm{E^\circ_{cell}}\) for magnesium is smaller than the \(\mathrm{E^\circ_{cell}}\) for iron, and it will be the metal that is targeted for oxidation. Thus, the head and tail of the nail would not corrode as long as magnesium is present.
2. If a metal is galvanized, that means it is coated with zinc, which is more active than the iron nail and will be oxidized. Even with a break in plating, the zinc is still more active and the iron won’t corrode.
3. If the metal is plated in copper, once the copper is broken, the iron is the more active metal and the nail will be oxidized and begin corrosion.

For review on this topic, visit the page "Electrochemistry 7: Electrochemical Corrosion".

Q19.63A

Calculate the amount in grams of metal that is deposited at the cathode by running a current of 3.15 A for 78 min in an electrolysis reaction for an aqueous solution containing a) \(\ce{Zn^2+}\) b) \(\ce{Sn^2+}\) c) \(\ce{Fe^3+}\) d) \(\ce{Ni^2+}\)

S19.63A

\(\mathrm{\textrm{# of mols of electrons}=\dfrac{(3.15\:A)(4680\:sec)}{(96485\:C)}=0.153\:mol\: e^-, \hspace{5 pt} since\: 78\:min \times \dfrac{60\:sec}{1\:min}}\)

1. \(\mathrm{0.153\:mol\: electrons \times \dfrac{1\:mol\: Zn}{2\:mol\: e^-} = 0.0765\:mol\: Zn \times \dfrac{65.41\:g}{1\:mol} = 5.00\:g\: Zn}\)
2. \(\mathrm{0.153\:mol\: electrons \times \dfrac{1\:mol\: Sn}{2\:mol\: e^-} = 0.0765\:mol\: Sn \times \dfrac{118.7\:g}{1\:mol} = 9.07\:g\: Sn}\)
3. \(\mathrm{0.153\:mol\: electrons \times \dfrac{1\:mol\: Fe}{3\:mol\: e^-} = 0.051\:mol\: Fe \times \dfrac{2.85\:g}{1\:mol} = 8.55\:g\: Fe}\)
4. \(\mathrm{0.153\:mol\: electrons \times \dfrac{1\:mol\: Ni}{2\:mol\: e^-} = 0.0765\:mol\: Ni \times \dfrac{58.69\:g}{1\:mol} = 4.49\:g\: Ni}\)

Q19.63B

How many grams of metal are deposited at cathode by passage of 2.30 A of current for 75 minutes in electrolysis of aqueous solution containing:

1. \(\ce{Mg^2+}\)
2. \(\ce{Sn^4+}\)
3. \(\ce{Fe^3+}\)
4. \(\ce{Ni^2+}\)

S19.63B

\(\mathrm{mol\:e^- = 75\:minutes \times \dfrac{60\:sec}{1\:min}\times \dfrac{2.30\:C}{1\:sec}\times\dfrac{1\: mol\: e^-}{96,485\:C} = 0.11\: mol\: e^- }\) \(\ce{Mr}\) for \(\mathrm{Mg = 24.31}\) \(\ce{Mr}\) for \(\mathrm{Sn = 118.71}\) \(\ce{Mr}\) for \(\mathrm{Fe = 55.85}\) \(\ce{Mr}\) for \(\mathrm{Ni = 58.69}\)

1. \(\mathrm{Mass\:Mg = 0.11\:mol\:e^- \times \dfrac{1\:mol\:Mg^{2+}}{2\:mol \:e^-}\times (Mr\:for\:Mg) = 1.34\:g\:Mg}\)
2. \(\mathrm{Mass\:Sn = 0.11\:mol\:e^- \times\dfrac{1\: mol\: Sn^{4+}}{4\: mol\: e^-}\times(Mr\: for\: Sn) = 3.26\: g\: Sn }\)
3. \(\mathrm{Mass\:Fe = 0.11\: mol\: e^- \times\dfrac{1\: mol\: Fe^{3+}}{3\: mol\: e^-}\times (Mr\: for\: Fe) = 2.05\: g\: Fe}\)
4. \(\mathrm{Mass\: Ni = 0.11\: mol\: e^- \times\dfrac{1\: mol\: Ni^{2+}}{2\: mol\: e^-}\times(Mr\: for\: Ni) = 3.23\: g\: Ni}\)

Q19.65A

Assuming all reactants and products are currently in their standard states, determine which of the following reactions occur spontaneously and which can occur only through the use of electrolysis. Also, for those that require electrolysis, determine what the minimum voltage required is.

1. \(\mathrm{Cu(s) + Zn^{2+}(aq) \rightarrow Cu^{2+}(aq) + Zn(s)}\)
2. \(\mathrm{2Al + 3Cu^{2+} \rightarrow 3Cu + 2Al^{3+}}\)
3. \(\mathrm{Zn + Cl_2(g) \rightarrow ZnCl_2(aq)}\)
4. \(\mathrm{2Fe^{3+} + 2Cl^- \rightarrow 2Fe^{2+} + Cl_2(g)}\)

S19.65A

1. Ox: \(\mathrm{Cu \rightarrow Cu^{2+} + 2e^- \hspace{47 pt}\quad E^\circ= -0.340\:V}\)

Red: \(\mathrm{Zn^{2+} + 2e^- \rightarrow Zn \hspace{42 pt}\quad E^\circ= -0.763\:V}\)
------------------------------------------------------------------------------
Overall: \(\mathrm{Cu + Zn^{2+} \rightarrow Cu^{2+} + Zn \quad E^\circ=-1.103}\)

Since voltage is negative, it requires electrolysis with an applied voltage of greater than 1.103 V

2. Red: \(\mathrm{Cu^{2+} + 2e^- \rightarrow Cu \hspace{38.5 pt} \quad E^\circ=0.340\:V}\)

Ox: \(\mathrm{Al \rightarrow Al^{3+} + 3e^- \hspace {49 pt}\quad E^\circ= 1.676\:V}\)
------------------------------------------------------------------------------
Overall: \(\mathrm{Cu^{2+} + Al \rightarrow Cu + Al^{3+} \quad E^\circ= 2.016\:V}\)

This is a spontaneous reaction under standard conditions because it has positive V.

3. Red: \(\mathrm{Cl_2 + 2e^- \rightarrow 2Cl^- \hspace{41 pt} \quad E^\circ= 1.358\:V}\)

Ox: \(\mathrm{Zn \rightarrow Zn^{2+} + 2e^- \hspace{49 pt} \quad E^\circ= 0.763\:V}\)
------------------------------------------------------------------------------
Overall: \(\mathrm{Cl_2 + Zn \rightarrow 2Cl^- + Zn^{2+} \quad E^\circ= 2.121\:V}\)

This is a spontaneous reaction under standard conditions because it has positive V.

4. Red: \(\mathrm{Fe^{3+} + e^- \rightarrow Fe^{2+} \hspace{62 pt}\quad E^\circ= 0.771\:V}\)

Ox: \(\mathrm{2Cl^- \rightarrow Cl_2(g) + 2e^- \hspace{55 pt}\quad E^\circ= -1.358\:V}\)
-------------------------------------------------------------------------------------
Overall: \(\mathrm{Fe^{3+} + 2Cl^- \rightarrow Fe^{2+} + Cl_2(g) \quad E^\circ= -0.587\:V}\)

Since the V is negative, it requires electrolysis with an applied V of greater than 0.587 V.

Q19.65B

Which of the following reactions are spontaneous under standard conditions? If the reaction is not spontaneous, determine its minimum voltage applied to undergo electrolysis.

1. \(\mathrm{Sn^{2+}(aq) + Zn^{2+} (aq) \rightarrow Zn(s)+ Sn^{4+}(aq)}\)
2. \(\mathrm{Li^+ (aq) + Fe^{2+}(aq)\rightarrow Li(s) + Fe^{3+}(aq) }\)
3. \(\mathrm{2H_2(g) + O_2(g)\:[in\: 1\: M\: H^+ (aq)] \rightarrow 2H_2O(l)}\)
4. \(\mathrm{2Al^{3+}(aq) + 3Pb(s)\rightarrow 3Pb^{2+}(aq) + 2Al(s) }\)

S19.65B

1. Anode: \(\mathrm{Sn^{2+}(aq)\rightarrow Sn^{4+}(aq) + 2e^-\quad E^\circ_{cell} = +0.154\: V}\)

Cathode: \(\mathrm{Zn^{2+}(aq) + 2e^- \rightarrow Zn(s) \hspace{6 pt} \quad E^\circ_{cell} = -0.763\: V}\)

\(\mathrm{E^\circ_{cell}= -0.763\: V - (+0.154\: V) = -0.917 \:V}\)

Minimum voltage needed to be applied to undergo electrolysis \(\mathrm{= +0.917\: V}\)

2. Anode: \(\mathrm{Fe^{2+}(aq) \rightarrow Fe^{3+}(aq) + e^- \quad E^\circ_{cell} = +0.771\: V}\)

Cathode: \(\mathrm{Li^+(aq)+ e^- \rightarrow Li(s)\hspace{14.5 pt}\quad E^\circ_{cell} = -3.040\:V}\)

\(\mathrm{E^\circ_{cell}= -3.040\:V - (+0.771\:V) = -3.811\:V}\)

Minimum voltage needed to be applied to undergo electrolysis \(\mathrm{= +3.811\: V}\)

3. Anode: \(\mathrm{2H_2(g)\rightarrow 4H^+(aq) + 4e^- \hspace{54 pt}\quad E^\circ_{cell} = +0.000\: V}\)

Cathode: \(\mathrm{O_2(g) + 4H^+ (aq) + 4e^- \rightarrow 2H_2O(l) \quad E^\circ_{cell} = +1.229\:V}\)

\(\mathrm{E^\circ_{cell}= +1.229\: V - (+0.000\: V) = +1.229\: V}\)

The reaction is spontaneous. No need undergo electrolysis.

4. Anode: \(\mathrm{Pb(s) \rightarrow Pb^{2+}(aq) + 2e^- \hspace{4.5 pt}\quad E^\circ_{cell} = -0.125\:V }\)

Cathode: \(\mathrm{Al^{3+}(aq) + 3e^- \rightarrow Al(s)\quad E^\circ_{cell} = -1.676\:V}\)

\(\mathrm{E^\circ_{cell}= -1.676\:V -(-0.125\:V) = -1.551\:V}\)

Minimum voltage needed to be applied to undergo electrolysis \(\mathrm{= +1.551\: V}\)

Q19.65C

Out of the reactions given below, which of the following can occur spontaneously only through electrolysis. For those requiring electrolysis, what is the minimum voltage required?

1. \(\mathrm{I_2(s) + Ni (s)\rightarrow 2I^- + Ni^{2+}}\)
2. \(\mathrm{Br_2(aq) + 2Fe^{2+} \rightarrow 2Br^- + 2Fe^{3+}}\)
3. \(\mathrm{Ni^{2+} + 2Cl^-(aq) \rightarrow Ni(s) + Cl_2(g)}\)
4. \(\mathrm{Cr^{2+}(aq) + Fe^{3+}(aq) \rightarrow Cr^{3+}(aq) + Fe^{2+}(aq)}\)

S19.65C

1. First, set up reduction and oxidation half reactions and calculate the \(\mathrm{E^\circ_{cell}}\) for the equation.

Reduction: \(\mathrm{I_2 + 2e^- \rightarrow 2I^-}\) and the value is 0.535

Oxidation: \(\mathrm{Ni (s) \rightarrow Ni^{2+}(aq) + 2e^-}\) with a value of -0.257

Thus, the \(\mathrm{E^\circ_{cell}}\) is \(0.535 -(-0.257) = 0.792\) and it is spontaneous under current conditions.

2. Set up reduction and oxidation half reactions and calculate the \(\mathrm{E^\circ_{cell}}\) for the equation.

Reduction: \(\mathrm{Br_2(aq) + 2e^{-} \rightarrow 2Br^-}\)

Oxidation: \(\mathrm{2Fe^{2+} \rightarrow 2e^{-}+ 2Fe^{3+}}\)

Thus, the \(\mathrm{E^\circ_{cell}}\) is 0.32 V and the \(\mathrm{E^\circ_{cell}}\) is positive, so no voltage needs to be applied and the cell is spontaneous under current conditions

3. Set up reduction and oxidation half reactions and calculate the \(\mathrm{E^\circ_{cell}}\) for the equation.

Reduction: \(\mathrm{Ni^{2+}(aq) + 2e^{-} \rightarrow Ni(s)}\)

Oxidation: \(\mathrm{2Cl^-(aq) \rightarrow Cl_2(g) + 2e^-}\)

Thus, the \(\mathrm{E^\circ_{cell}}\) is -1.59. This \(\mathrm{E^\circ_{cell}}\) is negative. This means that we would need to apply a minimum of 1.59 V to force the reaction to start, and get the \(\mathrm{E^\circ_{cell}}\) to be positive.

4. Set up reduction and oxidation half reactions and calculate the \(\mathrm{E^\circ_{cell}}\) for the equation.

Reduction: \(\mathrm{Fe^{3+}+e^{-} \rightarrow Fe^{2+}(aq)}\)

Oxidation: \(\mathrm{Cr^{2+}(aq)\rightarrow Cr^{3+}(aq)+e^{-}}\)

Thus, the \(\mathrm{E^\circ_{cell}}\) is 1.195 V so it is spontaneous at present conditions and does not need any additional voltage.

For review on this topic, visit the page "Electrochemistry 8: Electrolytic cells and electrolysis".

Q19.72A

Consider the two following reduction half reactions:

\[\mathrm{Sn^{4+} +2e^- \rightarrow Sn^{2+}}\]

\[\mathrm{Sn^{2+} +2e^- \rightarrow Sn(s)}\]

Calculate the \(\mathrm{E^\circ_{reduction}}\) for the reaction

\[\mathrm{Sn^{4+} +4e^- \rightarrow Sn (s)}\]

S19.72A

We will need to combine these equations, but we can’t simply add the \(\mathrm{E^\circ_{cell}}\) values together. We will need to convert and find the \(\mathrm{\Delta G}\) values for each equation. First, find the \(\mathrm{E^\circ_{cell}}\) of the two given half reactions: they are 0.154 V, and -0.137 V respectively from Table P2.

The \(\mathrm{\Delta G}\) of the first equation

\[ \mathrm{\Delta G^{\circ}} = \mathrm{n\, F \, E^{\circ}_{cell}}\]

Plugging in the values given will simplify to

\[\mathrm{ = -2 \, F \, (0.154) }\]

\[ \mathrm{\Delta G^{\circ}} = \mathrm{2 \, F \, (0.154)}\]

where \(\ce{F}\) is Faraday's constant.

2^nd equation \(\mathrm{ = -2 ^* F ^* (-0.137) }\)

\(\mathrm{\Delta G}\) for the desired equation \(\mathrm{= (-0.308F) V + (0.274F)V}\)

\(\mathrm{\Delta G = (-0.034F)V}\)

Now to find the \(\mathrm{E^{\circ}_{cell} = \left (\dfrac{(-0.034F)V}{4 F} \right )\, ^* \,V = -0.0085\:V = E^{\circ}_{cell}}\)

For review on this topic, visit the page "Electrochemistry 5: Applications of the Nernst Equation".

Q19.75A

In the two galvanic cells created the following variations occur:

\[\mathrm{L^{2+}(aq) + LO^{2+}(aq) + 2H^+(aq) \rightarrow 2L^{3+}(aq) + H_2O(l) \;\;\;\;\;\;\;\;\;\;E^\circ= 0.616 \:V}\]

\[\mathrm{L^{3+}(aq) + Ag^+(aq) + H_2O \rightarrow LO^{2+}(aq) + 2H^+ + Ag(s) \;\;\;\;\;\;\;\;\;\;E^\circ= 0.439\: V}\]

Use other values as well as the data presented here to determine \(\mathrm{E^\circ}\) for the half reaction:

\[\mathrm{L^{3+} + e^- \rightarrow L^{2+}}\]

S19.75A

Ox: \(\mathrm{L^{3+} + H_2O \rightarrow LO^{2+} + 2H^+ + e^- \quad {-E}^\circ_a}\)
Red: \(\mathrm{Ag^+ + e^- \rightarrow Ag(s) \hspace{61.5 pt}\quad E^\circ= 0.800\:V}\)
------------------------------------------------------------------------------------
Overall: \(\mathrm{\hspace{132.5 pt}\quad E^\circ=0.439\:V}\)

\(\mathrm{0.439\:V= {-E}_a + 0.800\:V}\)

\(\mathrm{E_a= 0.361\:V}\)

Ox: \(\mathrm{L^{2+} \rightarrow L^{3+} + e^- \hspace{69 pt}\quad {-E}^\circ_b}\)
Red: \(\mathrm{LO^{2+} + 2H^+ + e^- \rightarrow L^{3+} + H_2O \quad E^\circ= 0.361\:V}\)
------------------------------------------------------------------------------------
Overall: \(\mathrm{\hspace{128 pt}\quad E^\circ= 0.616\:V}\)

\(\mathrm{0.616\:V={-E}_b +0.361\:V}\)

\(\mathrm{E_b= -0.255\:V}\)

Q19.75B

Using reactions below, calculate \(\mathrm{E_{cell}}\) for \(\mathrm{X^{3+}(aq) + e^- \rightarrow X^{2+}(aq)}\)_.

\(\mathrm{X^{2+}(aq) + XO^{2+}(aq) + 2H^+(aq)\rightarrow 2X^{3+}(aq) + H_2O(l) \hspace{44 pt}\quad E^\circ_{cell}= 0.789\: V}\)

\(\mathrm{X^{3+}(aq) + Fe^{3+}(aq)+ H_2O(l)\rightarrow XO^{2+}(aq)+2H^+(aq)+ Fe^{2+}(aq)\quad E^\circ_{cell}= 0.243\: V}\)

S19.75B

First we must know that what are the reactions on the both side

Oxidation: \(\mathrm{X^{3+}(aq) + H_2O(l)\rightarrow XO^{2+}(aq) + 2H^+(aq) + e^- \hspace{45 pt}\quad -E^\circ_a}\)

Reduction: \(\mathrm{Fe^{3+}(aq) + e^- \rightarrow Fe^{2+}(aq) \hspace{144 pt}\quad E^\circ_{cell} = +0.771\: V}\)

Then we can get the net equation by combing these two reactions:

Net: \(\mathrm{X^{3+}(aq) + H_2O(l) + Fe^{3+}(aq) \rightarrow XO^{2+}(aq) + 2H^+(aq) + Fe^{2+}(aq)\quad E^\circ_{cell} = +0.243\:V }\)

As we know that E^°_cell = E^°_{c -} E^°_a, and in this case

\(\mathrm{E^\circ_{cell} = +0.771\:V - E^\circ_a}\)

\(\mathrm{0.243\:V = +0.771\:V - E^\circ_a}\)

\(\mathrm{E^\circ_a = 0.528\:V}\)

Thus, now we get: Oxidation: \(\mathrm{X^{2+}(aq) \rightarrow X^{3+}(aq) + e^- \hspace{94 pt}\quad -E^\circ_b}\)

Reduction: \(\mathrm{XO^{2+}(aq) + 2H^+(aq) + e^- \rightarrow X^{3+}(aq) + H_2O(l)\hspace{4 pt}\quad E^\circ_a = + 0.528\: V}\)

Net: \(\mathrm{X^{2+}(aq) + XO^{2+}(aq) + 2H^+(aq) \rightarrow 2X^{3+}(aq) + H_2O(l)\quad E^\circ_{cell} = + 0.789\: V}\)

Then we use the equation again:

\(\mathrm{E^\circ_{cell} = 0.528\:V - E^\circ_b}\) \(\mathrm{0.789\:V = 0.528\:V - E^\circ_b}\) \(\mathrm{E^\circ_b = - 0.261\:V}\) Thus \(\mathrm{X^{3+}(aq) + e^- \rightarrow X^{2+}(aq)\quad E^\circ_{cell} = - 0.261 \:V}\)

Q19.82A

A fuel cells is based on the reaction

\[\mathrm{CH_4(g) + 2O_2(g) \rightarrow CO_2(g) + 2H_2O (l)} \]

The theoretical \(\mathrm{E^\circ_{cell}}\) of this fuel cells is 0.92 V. Calculate a value of \(\mathrm{\Delta G_f^\circ}\) for \([\mathrm{CH_4(g)}]\).

S19.82A

Calculate \(\mathrm{\Delta G^\circ}\): \(\mathrm{n=8}\) (8 moles of e^- transferred)
\(\mathrm{\Delta G^\circ= -nFE^\circ_{cell}}\)
\(\begin{align}
\mathrm{\Delta G^\circ}
& = \mathrm{-8\: mol\: e^- (96845\: C/mol\: e^-) (0.92\:V)} \\
& = -7.101 \times 10^5\: \mathrm J = -710.1\: \mathrm{KJ}
\end{align}\)
Now to determine \(\mathrm{\Delta G_f^\circ}\) for \([\mathrm{CH_4(g)}]\)
\(\mathrm{-710.0\:KJ=\Delta G_f^\circ[CO_2(g)] + 2\Delta G_f^\circ[H_2O(l)] - \Delta G_f^\circ[CH_4(g)] - 2\Delta G_f^\circ[O_2(g)]}\)
\(\mathrm{-710.0\: KJ= -394.4\: KJ + 2(-237.1\: KJ) -\Delta G_f^\circ[CH_4(g)] - 0}\)
\(\mathrm{-158.5\: KJ= \Delta G_f^\circ[CH_4(g)]}\)

Q19.82B

Calculate \(\mathrm{\Delta G_f^\circ}\) for \(\ce{[CH4]}\) using \(\mathrm{E^\circ_{cell} = 1.191\: V}\) for fuel cell reaction: \(\mathrm{CH_4(g) + 2O_2(g) \rightarrow CO_2(g) + 2H_2O(l)}\) Given that:

\(\mathrm{\Delta G_f^\circ \,[CO_2(g)] = -394.4\: kJ\: mol^{-1}}\)

\(\mathrm{\Delta G_f^\circ \,[H_2O(l)] = -237.1 \:kJ \:mol^{-1}}\) \(\mathrm{\Delta G_f^\circ \,[ O_2(g) ] = 0.00\: kJ \:mol^{-1}}\)

S19.82B

\(\mathrm{\Delta G^\circ = -nFE^\circ_{cell} = \sum \Delta G_f^\circ}\) \(\mathrm{\Delta G^\circ = -(8 e^-)(96,485\:C/mol\:e^-)(1.191\:V)(1/1000\:kJ) = -919.31\: kJ/mol}\) \(\mathrm{\Delta G^\circ = \Delta G_f^\circ \,[CH_4(g)] + 2\Delta G_f^\circ \,[O_2(g)] - \Delta G_f^\circ \,[CO_2(g)] - 2 \Delta G_f^\circ \,[H_2O(l)]}\) \(\mathrm{\Delta G^\circ = \Delta G_f^\circ \,[CH_4(g)] + 2(0) - 394.4 + 2(-237.1)}\) \(\mathrm{-919.31 = \Delta G_f^\circ \,[CH_4(g)] + -868.6}\) \(\mathrm{\Delta G_f^\circ \,[CH_4(g)] = -50.71 \:kJ\: mol^{-1}}\)

Q19.82C

The \(\mathrm{E^\circ_{cell}}\) is 0.323 V for the following reaction under non-standard conditions

\[\mathrm{Zn (s) + Fe^{2+}(aq) \rightarrow Zn^{2+}(aq) + Fe(s)}\]

Calculate a \(\mathrm{\Delta G}\) value for \(\ce{[Fe^2+]}\).

S19.82C

Using the Nernst equation, we find the \(\mathrm{\Delta G}\) for the overall reaction.

The Nernst equation sets up as \(\mathrm{\Delta G = -zFE^{\circ}_{cell}}\) and we can plug in our values. The moles of electrons transferred in the reaction is 2. After plugging in 2 for \(\mathrm{z}\) and the given \(\mathrm{E^\circ_{cell}}\) along with Faraday’s constant, we find that \(\mathrm{\Delta G =-62.3283\:KJ}\).

Next, we find the \(\mathrm{\Delta G}\) stepwise by using our reaction along with a table of \(\mathrm{\Delta G}\) values found in the back of your textbook.

We must realize that the half reactions are Zn(s)->Zn 2+ +2e and 2e+ Fe2+->Fe(s). According to the table we can find the the values for the reactions in regard to their direction which are 0.763V of the cathode (Zn being oxidized) and -0.440V of the anode (Fe2+ being reduced).

This sets up as \(\mathrm{\Delta G = \Delta G[Zn^{2+}] -\Delta G[Fe^{2+}]}\) because we don’t account for the solids.

We must then plug in -62.3283 kj for Delta G and multiply by these concentrations. Solving for Fe2+, we can conclude that it's Delta G is -84.77 kj. We cannot come to this conclusion without using the Half reactions table in the back. We are also unable to find these answers without finding the overall Delta G for the reaction as a whole.

The resulting \(\ce{[Fe^2+]}\) value is -84.77 KJ so in this specific reaction, this is the desired \(\mathrm{\Delta G}\).

The link below provides additional examples of solving Nearst Equations in various forms:

www.youtube.com/watch?v=iKNFEjYDnts

For review on this topic, visit the page "Electrochemistry 8: Electrolytic cells and electrolysis".

Q19.90A

\(\ce{Pb^2+(aq)}\) and \(\ce{Ag+(aq)}\) were produced when 0.978 g sample of nitric acid was dissolved. After diluting the solution to 250.0 mL of deionized water, a silver electrode was placed in solution. The potential difference read 0.273 V. Calculate the mass of \(\ce{Ag}\) in the sample as a percent.

S19.90A

Oxidation: \(\mathrm{H_2(g) \rightarrow 2H^+(aq) + 2e^- \hspace{38 pt}\quad {-E}^\circ=0.00\:V}\)
Reduction: \(\mathrm{(Ag^+(aq) + e^- \rightarrow Ag(s) ) \times2 \hspace{23 pt}\quad E^\circ=0.800\:V}\)
Net: \(\mathrm{H_2(g) + 2Ag^+(aq) \rightarrow 2H^+(aq) + 2Ag(s) \quad E^\circ_{cell}= 0.800\:V}\)

\(\begin{align}
\mathrm{E_{cell}} & = \mathrm{E^\circ_{cell}-\dfrac{0.0592}{2}\log\dfrac{[H^+]^2}{[Ag^+]^2}} \\
& =\mathrm{0.800\:V-\dfrac{0.0592}{2}\log\dfrac{[1.00]^2}{[Ag^+]^2}=0.273\:V}
\end{align}\)
\(\mathrm{\log\dfrac{1}{[Ag^+]^{2}}=17.804}\)
\(\mathrm{[Ag^+]=1.25\times10^{-9}}\)

\(\mathrm{mass\:Ag= 250\:mL\times\dfrac{1\:L}{1000\:mL}\times\dfrac{1.25\times10^{-9}\:mol\: Ag^+}{1\:L}\times\dfrac{1\: mol\: Ag}{1\:mol\:Ag^+}\times\dfrac{107.87\: Ag}{1\: mol\: Ag}= 3.38\times10^{-8}\:g\: Ag}\)

\(\mathrm{\%\:Ag= \dfrac{3.38\times10^{-8}\: g\: Ag}{0.978\: g} \times 100 = 3.46\times10^{-6}\%}\)

Q19.90B

% of \(\ce{Ag}\) in \(\mathrm{Pb}\) was: 1.065 g sample was dissolved in nitric acid to produce \(\ce{Pb^2+}\) and \(\ce{Ag+}\). The solution was then diluted to 400 mL with water. An \(\ce{Ag}\) electrode was immersed in solution and the potential difference between electrode and SHE was 0.604 V. What was \(\mathrm{\%\: Ag}\) by mass in the Pb material?

S19.90B

Oxidation: \(\mathrm{H_2(g) \rightarrow 2H^+(aq) + 2e^- \hspace{12 pt}\quad E^\circ_{cell} = +0.00\:V}\)

Reduction: \(\mathrm{2Ag^+(aq) + 2e^- \rightarrow 2Ag(s) \quad E^\circ_{cell} = +0.800\:V }\)

\(\mathrm{E^\circ_{cell} = +0.800\:V - (+0.00\:V) = 0.800\:V}\)

\(\mathrm{E_{cell} = E^\circ_{cell} - \dfrac{0.0592}{n}\log \dfrac{[H^+]^2}{[Ag^+]^2}}\)

\(\mathrm{0.604\: V = 0.800\:V -\dfrac{0.0592}{2}\log\dfrac{[1.00]^2}{[Ag^+]^2}}\) \(\mathrm{[Ag^+] = 4.89 \times 10^{-4}\: M}\) \(\begin{align} \textrm{Mass Ag} & = \mathrm{0.400\: L\times\dfrac{[Ag^+]}{1\:L}\times\dfrac{1\: mol\: Ag}{1\:mol\: Ag^+}\times Mr\: Ag}\\
& = \mathrm{0.400\: L\times(4.89 \times 10^{-4}\: M)\times \dfrac{Ag^+}{1\: L}\times\dfrac{1\: mol\: Ag}{1\:mol\: Ag^+}\times107.87\: g}\\& = \mathrm{0.0211\: grams}\end{align}\) \(\mathrm{\% Ag = \dfrac{mass\:Ag}{mass \:of\: sample}\times 100\% = \dfrac{0.0211}{1.065}\times 100\% = 1.98\%}\)

Q19.96A

A source of \(\ce{Cu}\) is recovered from lead. The percentage of \(\ce{Cu}\) in lead is determined from the following information: A 2 gram sample is dissolved in nitric acid to make \(\ce{Cu^2+}\) and \(\ce{Pb^2+}\). A copper electrode was immersed in 750 mL of water. The potential was found to be 0.250 V. What was the % Copper recovered from the lead metal? Assume that \(\ce{Pb^2+}\) is ignored by the copper electrode.

S19.96A

Identify the oxidation/reduction reactions first.

Oxidation: \(\mathrm{H_2(g) \rightarrow 2H^+(aq) + 2e^-}\) with an \(\mathrm{E^\circ_{cell}}\) value of 0

Reduction: \(\mathrm{Cu^{2+}+2e^- \rightarrow Cu(s)}\) with an \(\mathrm{E^\circ_{cell}}\) value of 0.340

Thus the \(\mathrm{E^\circ_{cell}}\) is 0.340. We know that the \(\mathrm{E_{cell}}\) is 0.250 V so we can use the Nernst equation.

This will set up as \(\mathrm{0.250\;V = E^{\circ}_{cell} - \dfrac{0.0592}{n} \times \log Q}\)

Further values inputted will result in \(\mathrm{0.250 = 0.340 - \dfrac{0.0592}{2} \times \log \dfrac{[I]^2}{[Cu^{2+}]}}\)

Solve for the value of \(\ce{Cu^2+}\) using algebraic methods and we find that the concentration is 0.000911. We use this concentration and account for the mass in grams.

\(\begin{align} & \mathrm{0.750\;L\;(volume\;of\;solution)\times 0.000911 \times\dfrac{1\;mol\;Cu}{1\;mol\;Cu^{2+}}\times\dfrac{63.546\;g}{1\;mol\;Cu}\times\frac{1}{2}\;gram\;sample\;present \times 100\%} \\
& \mathrm{= 2.17\%\;copper\;results\;by\;mass}\end{align}\)

For review on this topic, visit the page "Electrochemistry 5: Applications of the Nernst Equation".