Standard Reduction Potential

Introduction

The standard reduction potential is in a category known as the standard cell potentials or standard electrode potentials. The standard cell potential is the potential difference between the cathode and anode. For more information view Cell Potentials. The standard potentials are all measured at 298 K, 1 atm, and with 1 M solutions.

Standard Reduction Potentials

As stated above, the standard reduction potential is the likelihood that a species will be reduced. It is written in the form of a reduction half reaction. An example can be seen below where "A" is a generic element and C is the charge.

• Standard Reduction Potential

\[ A^{C+} + C \,e^- \rightarrow A\]

For example, copper's Standard Reduction Potential of \(E^o =+0.340 \;V)\) is for this reaction:

\[ Cu^{2+} + 2 \,e^- \rightarrow Cu\]

Standard Oxidation Potentials

The standard oxidation potential is much like the standard reduction potential. It is the tendency for a species to be oxidized at standard conditions. It is also written in the form of a half reaction, and an example is shown below.

• Standard Oxidation Potential (SOP) under standard conditions:

\[ A(s) \rightarrow A^{c+} + C\,e^-\]

Copper's Standard Oxidation Potential

\[ Cu (s) \rightarrow Cu^{2+}+ 2e^- \]

\[ E_0^o (SOP) = -0.34\, V\]

The standard oxidation potential and the standard reduction potential are opposite in sign to each other for the same chemical species.

• Relation Between Standard Reduction Potential (SRP) and the Standard Oxidation Potential (SOP)

\[ E_0^o (SRP) = -E_0^o (SOP)\]

How are Standard Reduction Potentials Experimentally Determined

Standard reduction or oxidation potentials can be determined using a SHE (standard hydrogen electrode).

Figure \(\PageIndex{1}\): Standard Hydrogen Electrode

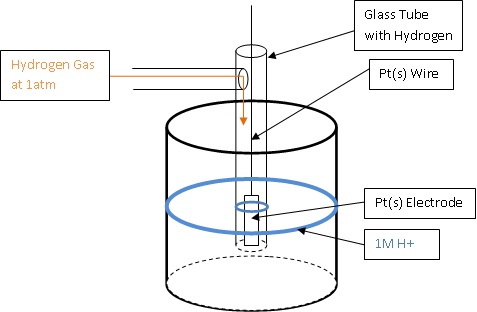
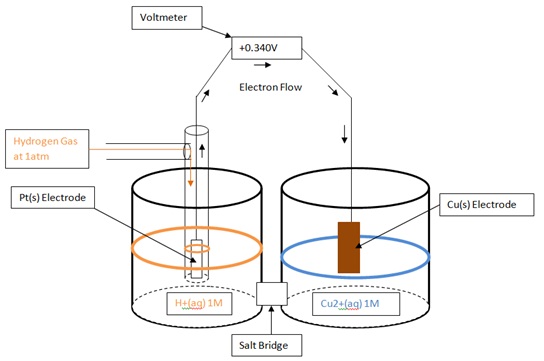
Universally, hydrogen has been recognized as having reduction and oxidation potentials of zero. Therefore, when the standard reduction and oxidation potential of chemical species are measured, it is actually the difference in the potential from hydrogen. By using a galvanic cell in which one side is a SHE, and the other side is half cell of the unknown chemical species, the potential difference from hydrogen can be determined using a voltmeter. Standard reduction and oxidation potentials can both be determined in this fashion. When the standard reduction potential is determined, the unknown chemical species is being reduced while hydrogen is being oxidized, and when the standard oxidation potential is determined, the unknown chemical species is being oxidized while hydrogen is being reduced. The following diagrams show how a standard reduction potential is determined.

• Figure (2) - Determining the Standard Reduction Potential of Copper
• Cu²⁺(aq)+2e^- → Cu(s) E= +0.34

How are Standard Reduction Potentials Applied

Standard reduction potentials are used to determine the standard cell potential. The standard reduction cell potential and the standard oxidation cell potential can be combined to determine the overall Cell Potentials of a galvanic cell. The equations that relate these three potentials are shown below:

\[ E^o_{cell} = E^o_{reduction} \text{ of reaction at cathode} + E^o_{oxidation} \text{ of reaction at anode}\]

or alternatively

\[ E^o_{cell} = E^o_{reduction} \text{ of reaction at cathode} - E^o_{reduction} \text{ of reaction at anode}\]

The Activity Series

When solving for the standard cell potential, the species oxidized and the species reduced must be identified. This can be done using an activity series. The table shown below is simply a table of standard reduction potentials in decreasing order. The species at the top have a greater likelihood of being reduced while the ones at the bottom have a greater likelihood of being oxidized. Therefore, when a species at the top is coupled with a species at the bottom, the one at the top will become reduced while the one at the bottom will become oxidized. Below is a table of standard reduction potentials.

Reduction Half-Reaction	Standard Reduction Potential (V)
F2(g)+2e^- → 2F^-(aq)	+2.87
S2O8^2^-(aq)+2e^- → 2SO4^2^-(aq)	+2.01
O2(g)+4H^+(aq)+4e^- → 2H2O(l)	+1.23
Br2(l)+2e^- → 2Br^-(aq)	+1.09
Ag^+(aq)+e^- → Ag(s)	+0.80
Fe^3^+(aq)+e^- → Fe^2^+(aq)	+0.77
I2(l) + 2e^- → 2I^-(aq)	+0.54
Cu^2^+(aq)+2e^- → Cu(s)	+0.34
Sn^4^+(aq)+2e^- → Sn^2^+(aq)	+0.15
S(s)+2H^+(aq)+2e^- → H2S(g)	+0.14
2H^+(aq)+2e^- → H2(g)	0.00
Sn^2^+(aq)+2e^- → Sn(g)	-0.14
V^3^+(aq)+e^- → V^2^+(aq)	-0.26
Fe^2^+(aq)+2e^- → Fe(s)	-0.44
Cr^3^+(aq)+3e^- → Cr(s)	-0.74
Zn^2^+(aq)+2e^- → Zn(s)	-0.76
Mn^2^+(aq)+2e^- → Mn(s)	-1.18
Na^+(aq)+e^- → Na(s)	-2.71
Li^+(aq)+e^- → Li(s)	-3.04

References

1. Petrucci, Harwood, Herring, and Madura. General Chemistry: Principles and Modern Applications. 9th ed. Upper Saddle River, New Jersey: Pearson Education, 2007.
2. Zhumdal, Zhumdal. Chemistry. 7th ed. Boston, New Jersey: Massachusetts Houghton Miffle Company, 2007.

True or False

1. Hydrogen has oxidation potentials of 0.
2. The standard oxidation potential is not much like the standard reduction potential.
3. The standard reduction cell potential and the standard oxidation cell potential can never be combined.

Solutions

1. True
2. False: the standard oxidation potential is much like the standard reduction potential
3. False: The standard reduction cell potential and the standard oxidation cell potential can be combined to determine the overall cell potential

Practice Problems

1. What does the standard reduction potential measure?
2. What are the differences between the standard reduction potential and standard oxidation potential, and how are the two related?
3. What conditions must be met for a potential to be standard?
4. When standard reduction potentials are measured, what are the potentials relative to?
5. How is a standard reduction potential measured?
6. Explain how the activity series is used.
7. Based on the activity series, which species will be oxidized and reduced: Zn²⁺ or H⁺.
8. Explain how standard reduction potentials or standard oxidation potentials are applied.
9. Draw and label a SHE.
10. The standard reduction potential of Fe³⁺ is +0.77V. What is its standard oxidation potential.

Solutions

1. Standard reduction potential measures the tendency for a given chemical species to be reduced.
2. The standard oxidation potential measures the tendency for a given chemical species to be oxidized as opposed to be reduced. For the same chemical species the standard reduction potential and standard oxidation potential are opposite in sign.
3. The cell must be at 298K, 1atm, and all solutions must be at 1M.
4. Standard reduction potentials are measured with relativity to hydrogen which has be universally set to have a potential of zero.
5. A standard reduction potential is measured using a galvanic cell which contains a SHE on one side and an unknown chemical half cell on the other side. The amount of charge that passes between the cells is measured using a voltmeter.
6. The activity series is a list of standard reduction potentials in descending order of the tendency for chemical species to be reduced. Species at the top are more likely to be reduced while species at the bottom are more likely to be oxidized.
7. H⁺ is farther up on the activity series then Zn²⁺ so H⁺ is reduced while Zn²⁺ is oxidized.
8. Standard reduction and oxidation potentials can be applied to solve for the standard cell potential of two different non hydrogen species. Examples can be seen in Cell Potentials.
9. See Figure (2).
10. The standard oxidation potential and standard reduction potential are always opposite in sign for the same species. The oxidation potential is -0.77V.

Contributors and Attributions

• Jiaxu Wang, Joslyn Wood, Esther Lee, Luvleen Brar (UCD)