10.3: Half Cells and Standard Reduction Potentials
- Page ID
- 84353
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
Much like \(G\) itself, \(E\) can only be measured as a difference, so a convention is used to set a zero to the scale. Toward this end, convention sets the reduction potential of the standard hydrogen electrode (SHE) to 0.00 V.
\[\ce{Zn \rightarrow Zn^{2+} + 2e^{-}} \nonumber \]
wtih \(E_{ox}^o = 0.763\, V\)
\[\ce{2 H^{+} + 2 e^{-} \rightarrow H2 } \nonumber \]
with \(E_{red}^o = 0.000 \,V\)
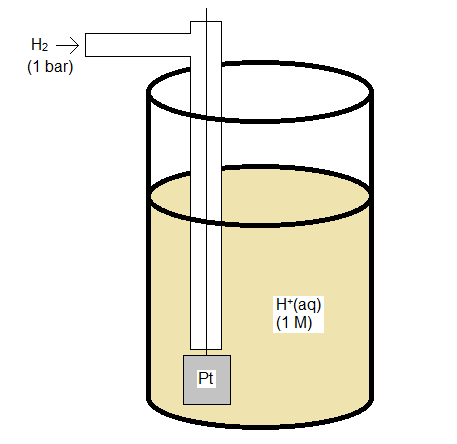
Standard Hydrogen Electrode
The standard hydrogen electrode is constructed so that H2 gas flows over an inert electrode made of platinum, and can interact with an acid solution which provides H+ for the half reaction
\[\ce{2 H^+(aq) + 2 e^{-} -> H_2(g)} \nonumber \]
Both H+ and H2 need to have unit activity (or fugacity), which if the solution and gas behave ideally means a concentration of 1 M and a pressure of 1 bar.
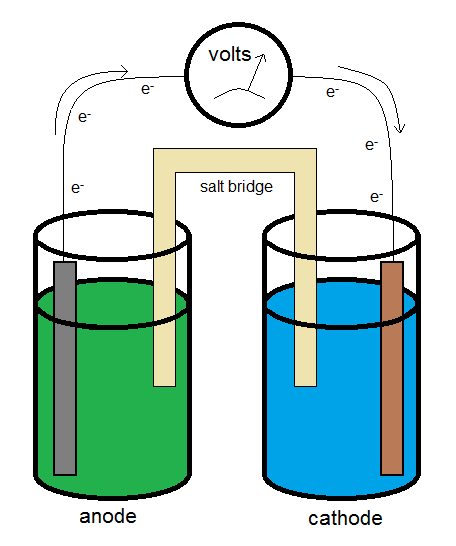
Electrochemical Cells
Standard reduction potentials can be measured relative to the convention of setting the reduction potential of the Standard Hydrogen Electrode (SHE) to zero. A number of values are shown in Table P1.
Which pair of reactants will produce a spontaneous reaction if everything is present in its standard state at 25 °C?
- \(\ce{Fe}\) and \(\ce{Cu^{2+}}\) or
- \(\ce{Fe^{2+}}\) and \(\ce{Cu}\)
Solution
The species with the standard reduction potential (Table P1) will force the other to oxidize.
From the table,
\[\ce{Cu^{2+} + 2 e^{-} \rightarrow Cu} \nonumber \]
with \(0.337\, V\)
\[ \ce{Fe^{2+} + 2 e^{-} \rightarrow Fe} \nonumber \]
with \(-0.440\, V\)
So the iron half-reaction will flip (so that iron is oxidizing) and the spontaneous reaction under standard conditions will be
\[Cu^{2+} + Fe \rightarrow Cu + Fe^{2+} \nonumber \]
with \(E^o = 0.777\, V\)
Calculating Cell Potentials
Using values measured relative to the SHE, it is fairly easy to calculate the standard cell potential of a given reaction. For example, consider the reaction
\[\ce{ 2 Ag^{+}(aq) + Cu(s) \rightarrow 2 Ag(s) + Cu^{2+}(aq)} \nonumber \]
Before calculating the cell potential, we should review a few definitions. The anode half reaction, which is defined by the half-reaction in which oxidation °Ccurs, is
\[\ce{Cu(s) \rightarrow Cu^{2+}(aq) + 2 e^{-}} \nonumber \]
And the cathode half-reaction, defined as the half-reaction in which reduction takes place, is
\[\ce{Ag^+(aq) + e- \rightarrow Ag(s)}\nonumber \]
Using standard cell notation, the conditions (such as the concentrations of the ions in solution) can be represented. In the standard cell notation, the anode is on the left-hand side, and the cathode on the right. The two are typically separated by a salt bridge, which is designated by a double vertical line. A single vertical line indicates a phase boundary. Hence for the reaction above, if the silver ions are at a concentration of 0.500 M, and the copper (II) ions are at a concentration of 0.100 M, the standard cell notation would be
Calculate the cell potential at 25 °C for the cell indicated by
\[\ce{Cu(s) | Cu^{2+}(aq, \,0.100\, M) || Ag^+ (aq,\, 0.500\, M) | Ag(s)} \nonumber \]
Solution
In order to calculate the cell potential (\(E\)), the standard cell potential must first be obtained. The standard cell potential at 25 °C is given by
\[\begin{align*} E_{cell} = E^o_{cathode} -E^o_{anode} \\[4pt] &= 0.799 \,V - 0.337\,V \\[4pt] &=0.462\,V \end{align*} \]
And for a cell at non-standard conditions, such as those indicated above, the Nernst equation can be used to calculate the cell potential. At 25 °C, The cell potential is given by
\[ \begin{align*} E_{cell} &= E^o_{cell} - \dfrac{RT}{nF} \ln \left( \dfrac{[Cu^{2+}]}{[Ag^+]} \right) \\[4pt] &= 0.462\,V - \dfrac{(8.314 \,J/(mol\,K) (298\,K) }{2(96484\,C)} \ln \left( \dfrac{0.100\,M}{0.500\,M} \right) \end{align*} \]
Noting that \(1\, J/C = 1\, V\),
\[E = 0.483\,V \nonumber \]
Calculate the cell potential at 25 °C for the cell defined by
\[Ni(s) | Ni^{2+}\, (aq, \,0.500\, M) || Cu(s) | Cu^{2+}(aq, \,0.100\, M) \nonumber \]
Solution
We will use the Nernst equation. First, we need to determine \(E^o\). Using Table P1, it is apparent that
\[ \ce{Cu^{2 }+ 2 e^{-} \rightarrow Cu } \nonumber \]
\(E^o = 0.337 \,V\)
\[\ce{ Ni^{2+} + 2 e^{-} \rightarrow Ni} \nonumber \]
with \(E^o = -0.250\, V\)
So copper, having the larger reduction potential will be the cathode half-reaction while forcing nickel to oxidize, making it the anode. So Eo for the cell will be given by
\[ \begin{align*} E_{cell} &= E^o_{cathode} -E^o_{anode} \\[4pt] &= 0.337 \,V -(-0.250\,V) \\[4pt] = 0.587\,V \end{align*} \]
And the cell potential is then given by the Nernst Equation
\[ \begin{align*} E_{cell} &= E^o_{cell} - \dfrac{RT}{nF} \ln Q \\[4pt] &= 0.587 - \dfrac{(8.314 \,J/(mol\,K) (298\,K) }{2(96484\,C)} \ln \left( \dfrac{0.500\,M}{0.100\,M} \right) \\[4pt] &= 0.566\,V \end{align*} \]
Measuring the Voltage
A typical galvanic electrochemical cell can be constructed similar to what is shown in the diagram above. The electrons flow from the anode (the electron source) to the cathode (the electron sink.) The salt bridge allows for the flow of ions to complete the circuit while minimizing the introduction of a junction potential.