10.4: Entropy of Electrochemical Cells

Last updated
Save as PDF

Page ID: 84354

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

The Gibbs function is related to entropy through its temperature dependence

\[ \left( \dfrac{\partial \Delta G}{\partial T} \right)_p = - \Delta S \nonumber \]

A similar relationship can be derived for the temperature variance of \(E^o\).

\[ nF \left( \dfrac{\partial E^o}{\partial T} \right)_p = \Delta S \label{eq2} \]

Consider the following data for the Daniel cell (Buckbeei, Surdzial, & Metz, 1969) which is defined by the following reaction

\[Zn(s) + Cu^{2+}(aq) \rightleftharpoons Zn^{2+}(aq) + Cu(s) \nonumber \]

T (°C)	0	10	20	25	30	40
Eo (V)	1.1028	1.0971	1.0929	1.0913	1.0901	1.0887

From a fit of the data to a quadratic function, the temperature dependence of

\[\left( \dfrac{\partial E^o}{\partial T} \right)_p \nonumber \]

is easily established.

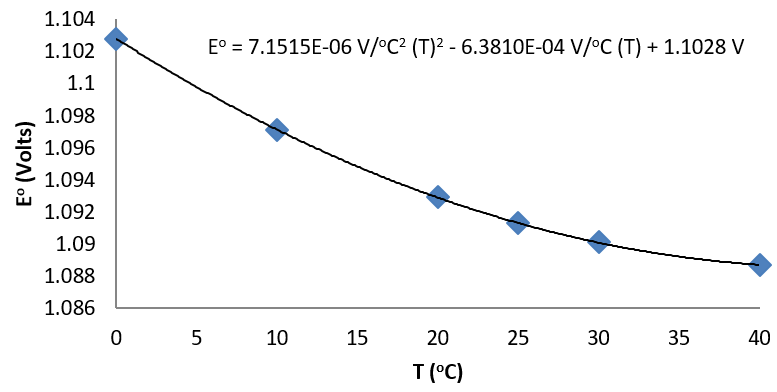
10.4.1a.png — Figure \(\PageIndex{1}\): Temperature dependence of the cell potential for a Daniel cell.

The quadratic fit to the data results in

\[\left( \dfrac{\partial E^o}{\partial T} \right)_p = 3.8576 \times 10^{-6} \dfrac{V}{°C^2}(T) - 6.3810 \times 10^{-4} \dfrac{V}{°C} \nonumber \]

So, at 25 °C,

\[\left( \dfrac{\partial E^o}{\partial T} \right)_p = -54166 \times 10^{-4} V/K \nonumber \]

noting that \(K\) can be substituted for \(°C\) since in difference they have the same magnitude. So the entropy change is calculated (Equation \ref{eq2}) is

\[ \Delta S = nF \left( \dfrac{\partial E^o}{\partial T} \right)_p = (2\,mol)(95484\,C/mol) (-5.4166 \times 10^{-4} V/K) \nonumber \]

Because

\[ 1\,C \times 1\,V = 1\,J \nonumber \]

The standard entropy change for the Daniel cell reaction at 25 °C is

\[ \Delta S = -104.5\, J/(mol\,K). \nonumber \]

It is the negative entropy change that leads to an increase in standard cell potential at lower temperatures. For a reaction such as

\[Pb(s) + 2 H^+(aq) \rightarrow Pb^{2+}(aq) + H_2(g) \nonumber \]

which has a large increase in entropy (due to the production of a gas-phase product), the standard cell potential decreases with decreasing temperature. As this is the reaction used in most car batteries, it explains why it can be difficult to start ones car on a very cold winter morning. The topic of temperature dependence of several standard cell potentials is reported and discussed by Bratsch (Bratsch, 1989).