16.5: Applications of the Nernst Equation

Learning Objectives

Make sure you thoroughly understand the following essential ideas:

• Atmospheric oxygen is a strong oxidizing agent, but in the absence of a suitable catalyst this reaction is ordinarily too slow to be observable.
• The pE is a useful index of electron availability, especially in natural waters and biological systems in which multiple redox systems are usually present.
• Solubility products can often be measured by constructing a cell in which one of the electrodes involves the sparingly soluble salt, and the net cell equation corresponds to the solubility reaction.
• Potentiometric titrations are widely used to measure concentrations of species that are readily oxidized or reduced.
• Measurement of pH is accomplished with an electrode consisting of a thin membrane of glass in which Na⁺ ions are exchanged with H⁺.
• Membrane (Donnan) potentials arise when passage of an ion across a semipermeable membrane is selectively facilitated or inhibited.
• Nerve conduction occurs not by a flow of charge through the nerve, but by a wave of depolarization resulting from the concerted action of active channels that govern the passage of ions (mainly K⁺ and Na⁺) across the membrane enclosing the nerve.

We ordinarily think of the oxidation potential being controlled by the concentrations of the oxidized and reduced forms of a redox couple, as given by the Nernst equation. Under certain circumstances it becomes more useful to think of E as an independent variable that can be used to control the value of Q in the Nernst equation. This usually occurs when two redox systems are present, one being much more concentrated or kinetically active than the other. By far the most important example of this is the way atmospheric oxygen governs the composition of the many redox systems connected with biological activity.

Oxygen and the Aquatic Environment

The presence of oxygen in the atmosphere has a profound effect on the redox properties of the aquatic environment— that is, on natural waters exposed directly or indirectly to the atmosphere, and by extension, on organisms that live in an aerobic environment.This is due, of course, to its being an exceptionally strong oxidizing agent and thus a low-lying sink for electrons from most of the elements and all organic compounds. Those parts of the environment that are protected from atmospheric oxygen are equally important because it is only here that electrons are sufficiently available to produce the "reducing" conditions that are essential for processes varying from photosynthesis to nitrogen fixation.

Example \(\PageIndex{1}\)

Estimate the redox potential of a natural water that is in equilibrium with the atmosphere at pH 7 and 298 K. What fraction of a dilute solution Fe²⁺ will be in its oxidized form Fe³⁺ in such a water?

Solution

The relevant E°s are

• 1.23 v for O₂(g) + 4H⁺ + 4e^–→ 2H₂O and
• 0.77 V for the Fe³⁺/Fe²⁺ couple.

(a) The potential (with respect to the SHE, of course) is given by the Nernst equation

which works out to E = 0.82 volt. As the Le Chatelier principle predicts, the higher pH (lower [H⁺] compared to that at the "standard" pH of zero) reduces the electron-accepting tendency of oxygen.

(b) The Nernst equation for the reduction of Fe³⁺ is E = .77–.059 log Q, in which Q is the ratio [Fe²⁺]/[Fe³⁺]. With E set by the O₂/H₂O couple, this becomes

0.82 = 0.77 – 0.059 log Q

which gives Q = 10^–0.85 or [Fe²⁺]/[Fe³⁺] = 0.14/1, so the fraction of the iron in its oxidized form is 1/1.14 = 0.88.

If we can have pH, why not pE?

As you will recall from your study of acid-base chemistry, the pH of a solution (defined as –log {H⁺}) is a measure of availablity (technically, the activity) of protons in the solution. As is explained in more detail here, protons tend to "fall" (in free energy) from filled donor levels (acids) to lower acceptor levels (bases.) Through the relation

\[[H^+] \approx K_a \dfrac{C_a}{C_b}\]

which can be rewritten as

\[\dfrac{C_a}{C_b} \approx \dfrac{[H^+]}{K_a}\]

in which the pH is treated as an independent variable that controls the ratio of the conjugate forms of any acid-base pairs in the solution:

\[\log \left(\dfrac{C_a}{C_b}\right) \approx pH – pK_a\]

In the same way, we can define the pE as the negative log of the electron activity in the solution:

\[pE = –\log{e^–}\]

of these particles (but not to their "concentrations") when we are considering their availability to donors and acceptors. We will not get into the details of how pE is actually calculated (it is of course related to the ordinary standard electrode potential). To get an idea of its significance, consider the following chart that shows the pE° values of some redox systems that are of immense importance in the aquatic environment.

Environmentally-important redox systems

• These pE values refer to typical environmental conditions with pH=7 and oxygen partial pressure of 0.21 atm. The scale below shows the free energy of a mole of electrons relative to their level in H₂O.
• The two conjugate forms of any redox pair are present in equal concentrations when the pE is at the level at which the pair is shown. At pE's above or below this level, the reduced or oxidized form will predominate.
• The sugar glucose, denoted by the general formula for carbohydrates {CH₂O}, is the source of chemical energy for most organisms. Note that it is thermodynamically stable (and thus capable of being formed by photosynthesis) only under highly reducing conditions.
• Organisms derive their metabolic free energy when electrons fall from glucose to a lower-lying acceptor on the right.
• Delivery of electrons from glucose to O₂ (8) is the source of metabolic free energy for all aerobic organisms, yielding 125 kJ per mole of electrons transferred.

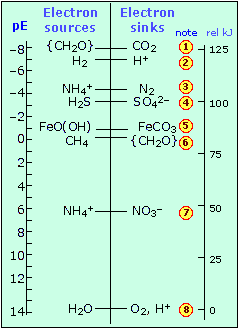
A few other points about this plot are worth noting:

• Anaerobic organisms must make do with electron-acceptors above oxygen. The poor bacteria that depend on reducing hydrogen ions (2) have it worst of all, gaining only a tiny amount of metabolic energy to produce a tiny puff of hydrogen gas.
• Reaction (3) is not much more efficient, but it is the vital first link in the process of natural nitrogen fixation that gets carried out in the protected electron-rich environment of the organisms that live in the root nodules of legumes.
• The consequences of (4) are readily apparent if you have ever noticed the rotten-egg odor of some poorly-aerated muddy soils.
• Reaction (6) is known as fermentation; it takes place in the anarobic soils of marshes and bogs (hence the nickname "marsh gas" for methane) and in the insides of animals from termites to cows, and sometimes to our embarrassment, in ourselves. Notice that glucose plays the double role of electron donor and acceptor here; this is a disproportionation reaction.
• Finally, if you have ever had much to do with babys' diapers, you have likely noticed the smell of ammonia produced as the anaerobic bacteria from within deliver electrons to nitrate ions (7). It's important to bear in mind that the reactions discussed above are mediated by living organisms; without the necessary enzymes to catalyze them, their rates are essentially zero.

For a more detailed chart, see Falling through the respiratory chain.

Analytical chemistry applications

A very large part of Chemistry is concerned, either directly or indirectly, with determining the concentrations of ions in solution. Any method that can accomplish such measurements using relatively simple physical techniques is bound to be widely exploited. Cell potentials are fairly easy to measure, and although the Nernst equation relates them to ionic activities rather than to concentrations, the difference between them becomes negligible in solutions where the total ionic concentration is less than about 10^–3 M.

The concentrations of ions in equilibrium with a sparingly soluble salt are sufficiently low that their direct determination can be quite difficult. A far simpler and common procedure is to set up a cell in which one of the electrode reactions involves the insoluble salt, and whose net cell reaction corresponds to the dissolution of the salt. For example, to determine the K_sp for silver chloride, we could use the cell

\[Ag_{(s)} | Ag^+(?\; M) || Ag^+,Cl^– | AgCl_{(s)} | Ag_{(s)}\]

whose net equation corresponds to the dissolution of silver chloride:

cathode:	AgCl(s) + e^– → Ag(s) + Cl^–(aq)	E° = +0.222 v
anode:	Ag(s) → Ag^+(aq) + e^–	E° = –(+0.799) v
net:	AgCl(s) → Ag^+ + Cl^–	E° = -0.577 v

The standard potential for the net reaction refers to a hypothetical solution in which the activities of the two ions are unity. The cell potential we actually observe corresponds to E in the Nernst equation, which is then solved for Q which gives K_sp directly.

Potentiometric titrations

In many situations, accurate determination of an ion concentration by direct measurement of a cell potential is impossible due to the presence of other ions and a lack of information about activity coefficients. In such cases it is often possible to determine the ion indirectly by titration with some other ion. For example, the initial concentration of an ion such as Fe²⁺ can be found by titrating with a strong oxidizing agent such as Ce⁴⁺. The titration is carried out in one side of a cell whose other half is a reference electrode:

Pt(s) | Fe²⁺, Fe³⁺ || reference electrode

Initially the left cell contains only Fe²⁺. As the titrant is added, the ferrous ion is oxidized to Fe³⁺ in a reaction that is virtually complete:

\[Fe^{2+} + Ce^{4+} → Fe^{3+} + Ce^{3+}\]

The cell potential is followed as the Fe²⁺ is added in small increments. Once the first drop of ceric ion titrant has been added, the potential of the left cell is controlled by the ratio of oxidized and reduced iron according to the Nernst equation

\[E = 0.68 - 0.059 \; \log \dfrac{]Fe^{3+}]}{[Fe^{2+}]}\]

which causes the potential to rise as more iron becomes oxidized.

Figure \(\PageIndex{1}\): potentiometric titration curve

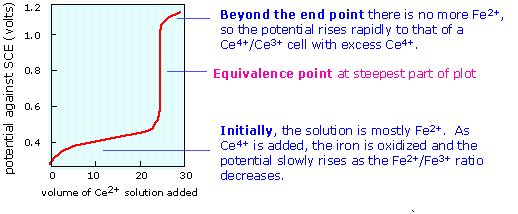
When the equivalence point is reached, the Fe²⁺ will have been totally consumed (the large equilibrium constant ensures that this will be so), and the potential will then be controlled by the concentration ratio of Ce³⁺/Ce⁴⁺. The idea is that both species of a redox couple must be present in reasonable concentrations poise an electrode (that is, to control its potential according to the Nernst equation.) If one works out the actual cell potentials for various concentrations of all these species, the resulting titration curve looks much like the familiar acid-base titration curve. The end point is found not by measuring a particular cell voltage, but by finding what volume of titrant gives the steepest part of the curve.

Measurement of pH

Since pH is actually defined in terms of hydrogen ion activity and not its concentration, a hydrogen electrode allows a direct measure of {H⁺} and thus of –log {H⁺}, which is the pH. All you need is to measure the voltage of a cell

H₂(g, 1 atm) | Pt | H⁺(? M) || reference electrode

In theory this is quite simple, but when it was first employed in the pre-electronics era, it required some rather formidable-looking apparatus (such as the L&N vibrating-reed electrometer setup from the 1920's shown here) and the use of explosive hydrogen gas. Although this arrangement (in which the reference electrode could be a standard hydrogen electrode) has been used for high-precision determinations since that time, it would be impractical for routine pH measurements of the kinds that are widely done, especially outside the research laboratory.

The glass electrode for pH measurements

In 1914 it was discovered that a thin glass membrane enclosing a solution of HCl can produce a potential that varies with the hydrogen ion activity {H⁺} in about the same way as that of the hydrogen electrode. Glass electrodes are manufactured in huge numbers for both laboratory and field measurements. They contain a built-in Ag-AgCl reference electrode in contact with the HCl solution enclosed by the membrane.

The potential of a glass electrode is given by a form of the Nernst equation very similar to that of an ordinary hydrogen electrode, but of course without the H₂:

E_membrane = A + (RT/F) ln ( {H⁺} + B )

in which A and B are constants that depend on the particular glass membrane.

The reason a glass membrane would behave in this way was not understood until around 1970. It now appears that hydrogen ions in the external solution diffuse through the glass and push out a corresponding number of the Na⁺ ions which are normally present in most glasses. These sodium ions diffuse to whichever side of the membrane has the lower concentration, where they remain mostly confined to the surface of the glass, which has a porous, gelatinous nature. It is the excess charge produced by these positive ions that gives rise to the pH-dependent potential. The first commercial pH meter was developed by Arnold Beckman (1900-2004) while he was a Chemistry professor at CalTech. He was unable to interest any of the instrumentation companies in marketing it, so he founded his own company and eventually became a multi-millionaire philanthropist.

Arnold Beckman	An early Beckman pH meter	A typical modern pH meter

Ion-selective electrodes

The function of the membrane in the glass electrode is to allow hydrogen ions to pass through and thus change its potential, while preventing other cations from doing the same thing (this selectivity is never perfect; most glass electrodes will respond to moderate concentrations of sodium ions, and to high concentrations of some others.) A glass electrode is thus one form of ion-selective electrode. Since about 1970, various other membranes have been developed which show similar selectivities to certain other ions. These are widely used in industrial, biochemical, and environmental applications.

Membrane potentials and nerve conduction

You may recall the phenomena of osmosis and osmotic pressure that are observed when two solutions having different solute concentrations are separated by a thin film or membrane whose porosity allows small ions and molecules to diffuse through, but which holds back larger particles. If one solution contains a pair of oppositely-charged ionic species whose sizes are very different, the smaller ions may pass through the semipermeable membrane while the larger ones are retained. This will produce a charge imbalance between the two solutions, with the original solution having the charge sign of the larger ion. Eventually the electrical work required to bring about further separation of charges becomes too large to allow any further net diffusion to take place, and the system settles into an equilibrium state in which a constant potential difference (usually around a volt or less) is maintained. This potential difference is usually called a membrane potential or Donnan potential after the English chemist who first described this phenomenon around 1930.

Origin of a membrane potential If the smaller ions are able to diffuse through the membrane but the larger ions cannot, a potential difference will develop between the two solutions. This membrane potential can be observed by introducing a pair of platinum electrodes.

The figure shows a simple system containing the potassium salt of a protein on one side of a membrane, and potassium chloride on the other. The proteinate anion, being too large to diffuse through the membrane, gives rise to the potential difference. The value of this potential difference can be expressed by a relation that is essentially the same as the Nernst equation, although its derivation is different. The membrane potential can be expressed in terms of the ratio of either the K⁺ or Cl^– ion activities:

The membrane surrounding most living cells contains sites or "channels" through which K⁺ ions are selectively transported so that the concentration of K⁺ inside the cell is 10-30 times that of the intracellular fluid. Taking the activity ratio as about 20, the above equation predicts that the potential difference θ_inside - θ_outside will be

which is consistent with observed values. Transport of an ion such as K⁺ from a region of low concentration into the more concentrated intercellular fluid requires a source of free energy, which is supplied by ATP under enzymatic control. The metabolic processes governing this action are often referred to as "ion pumps".

Nerve conduction

Transmission of signals through the nervous system occurs not by the movement of a charge carrier through the nerve, but by waves of differential ion concentrations that travel along the length of the nerve. These concentration gradients are reduced by protein-based ion channels and ATP-activated (and energy-consuming) ion pumps specific to K⁺ and Ca²⁺ ions.

Figure \(\PageIndex{2}\): Conduction of nerve impulses

We sometimes think of our nerves as the body's wiring, but the "electricity" that they transmit is not a flow of electrons, but a rapidly-traveling wave of depolarization involving the transport of ions through the nerve membrane. The normal potential difference between the inner and outer parts of nerve cells is about –70 mv as estimated above. Transmissin of a nerve impulse is initiated by a reduction of this potential difference to about –20 mv. This has the effect of temporarily opening the Na⁺ channel; the influx of these ions causes the membrane potential of the adjacent portion of the nerve to collapse, leading to an effect that is transmitted along the length of the nerve. As this pulse passes, K⁺ and Na⁺ pumps restore the nerve to its resting condition.

Summary

Make sure you thoroughly understand the following essential ideas which have been presented above. It is especially important that you know the precise meanings of all the highlighted terms in the context of this topic.

• Atmospheric oxygen is a strong oxidizing agent, but in the absence of a suitable catalyst this reaction is ordinarily too slow to be observable. In organisms that possess the appropriate enzymes, the reaction is sufficiently fast to control the availability of electrons to other redox systems.
• The pE is a useful index of electron availability, especially in natural waters and biological systems in which multiple redox systems are usually present. Although electrons tend to "fall" (in free energy) from sources to sinks, the outcome depends very strongly on the rates of the various reactions. This is quite different from proton-exchange (acid-base) reactions which are uniformly fast.
• Solubility products can often be measured by constructing a cell in which one of the electrodes involves the sparingly soluble salt, and the net cell equation corresponds to the solubility reaction.
• Potentiometric titrations are widely used to measure concentrations of species that are readily oxidized or reduced. The reaction must be fast and have a very large equilibrium constant. The equivalance point is detected by the rapid change in potential that occurs when control of the cell potential passes from the redox system of the analyte to that of the titrant.
• Measurement of pH is accomplished with an electrode consisting of a thin membrane of glass in which Na⁺ ions are exchanged with H⁺.
• Membrane (Donnan) potentials arise when passage of an ion across a semipermeable membrane is selectively facilitated or inhibited. The classic example is a sodium proteinate solution in which the protein anion is too large to pass through the membrane. In organisms, ion-specific channels or "pumps" have a similar effect.
• Nerve conduction occurs not by a flow of charge through the nerve, but by a wave of depolarization resulting from the concerted action of active channels that govern the passage of ions (mainly K⁺ and Na⁺) across the membrane enclosing the nerve.