14.E: Principles of Chemical Equilibria (Exercises)
- Page ID
- 11442
These are homework exercises to accompany the Textmap created for "General Chemistry: Principles and Modern Applications " by Petrucci et al. Complementary General Chemistry question banks can be found for other Textmaps and can be accessed here. In addition to these publicly available questions, access to private problems bank for use in exams and homework is available to faculty only on an individual basis; please contact Delmar Larsen for an account with access permission.
Q14.1
Looking at the following, write the balanced equation and Kc expression for each reversible reaction:
- the dissociation of water:
- the reaction between gaseous \(CO\) and \(NO_2\):
- the addition of Hydrogen Iodide to water:
Q14.2
Balance the equilibrium equation and determine the corresponding \(K_p\) expression for each reversible reaction.
- \(N_2O_4(g) \rightleftharpoons NO(g)\)
- \(Ag_2O(s) \rightleftharpoons Ag(s) + O_2(g)\)
- \(Cs_2(g) + H_2(g) \rightleftharpoons CH_4(g) + H_2S(g)\)
S14.2
a.) N2O4(g)↔2NO(g)
Kp = (PNO)2/(PN2O4)1
b.) Ag2O(s)↔2Ag(s) + (1/2)O2(g)
Kp = (PAg)2 x (PO2)1/2/(PAg2O)
c.) Cs2(g) + 4H2(g)↔CH4(g) +2 H2S(g)
Kp = (PCH4)1 x (PH2S)2/(PCs2)1 x (PH2)4
Q14.2
Based on the following, write a balanced equation and kp expression for each of the following:
- \(N_2(g)+ H_2(g) \rightleftharpoons NH_3(g)\)
- The thermal decomposition of \(CaCO_3\)
- The reaction of CO2 with a sodium hydroxide solution
Q14.3
Give the \(K_c\) expressions for the following reactions:
- \(2HI(g) + O_2(g) \rightleftharpoons 2HIO_2(g)\)
- \(ClNO_2(g) + NO(g) \rightleftharpoons NO_2(g) + ClNO(g)\)
- \(H_2(g) +I_2(g) \rightleftharpoons 2HI(g)\)
Q14.33
A mixture consisting of 0.201 mol \(H_2\), and 0.201 mol of \(I_2\) is brought to equilibrium at 500°C, in a 4.5 L flask. What are the equilibrium amounts of \(H_2\), \(I_2\), and \(HI\)? \(K_c = 50.2\) at 500°C
S14.33
Video Solution
0.201 mol H2 /4.5 L = 0.0447 M H2 (First calculate molarity)
0.201 mol I2/4.5 L = 0.0447 M I2
\[H_2 + I_2 \rightleftharpoons 2HI \] (Balance equation and set up ICE table)
| ICE TABLE | \(H_2\) | \(I_2\) | \(HI\) |
| I | 0.0447M | 0.0447 M | 0 |
| C | -X | -X | +2X |
| E | 0.0447-X | 0.0447-X | 2X |
\[K_c = \dfrac{2X}{(0.0447-X)^2}\]
\[50.2 = \dfrac{2X}{(0.0447-X)^2}\]
(use quad formula)
X=0.0264
[H2] = 0.0183 M
[I2] = 0.0183 M
[HI] = 0.0528 M
Q14.43
Cadmium metal is added to 0.500 L of 1 M an aqueous solution of \([Cr^{3+}]\). What are the concentrations of the different ionic species at equilibrium for the oxidation of \(Cd\) into \(Cd^{2+}_{(aq)}\):
\[2Cr^{3+}_{(aq)} + Cd_{(s)} \rightleftharpoons 2Cr^{2+}_{(aq)} + Cd^{2+}_{(aq)}\]
with \(K_c = 0.288\).
Solution
The ICE table is first constructed
| ICE | \([Cr^{3+}_{(aq)}]\) (M) | \(Cr^{2+}_{(aq)}\) (M) | \(Cd^{2+}_{(aq)}\) (M) |
| I | \(1\) | \(0\) | \(0\) |
| C |
\(-2x\) |
\(+2x\) |
\(+x\) |
| E | \(1-2x\) | \(2x\) | \(x\) |
Now construct the relationship for the equilibrium constant (do not include solid Cd in equilibrium):
\[K_c = \dfrac{[Cr^{2+}_{(aq)}]^2[Cd^{2+}_{(aq)}]}{[Cr^{3+}_{(aq)}]^2} \\ = \dfrac{(2x)^2(x)}{(1-2x)^2} \tag{1}\]
\[ \\ = \dfrac{4x^3}{(1-2x)^2} \tag{2}\]
Alternatively
\[ K_c (1-2x)^2 = 4x^3 \tag{3}\]
\[K_c - 4K_cx + 4K_cx^2 = 4x^3 \]
\[4x^3 - 4K_cx^2 + 4K_cx - K_c = 0 \tag{4}\]
This is unfortunately is a cubic equation and can be solved analytically, but not easily. It is typically solved either graphically or numerically. Before solving numerical, we can evaluate one alternative by assuming that \(x\) is small (\(x/2 << 1\)), then the equation 2 can be approximated and the cubic equation becomes solvable:
\[ \\ = \dfrac{4x^3}{(1-2x)^2} \approx 4x^3\]
\[ x \approx \sqrt[3]{\dfrac{K_c}{4}}\]
\[ x \approx \sqrt[3]{\dfrac{0.288}{4}} \approx 0.4160 \tag{5}\]
Unfortunately, this value for \(x\) is clearly not small and hence the approximate is incorrect. Hence, the solution requires a numerical approach to identify the roots of equation 4. By plotting \(4x^3 - 4K_cx^2 + 4K_cx - K_c\) vs. \(x\), the physical solution (i.e., root between \(x=0\) and \(x=1\)) can be resolved graphically (below).
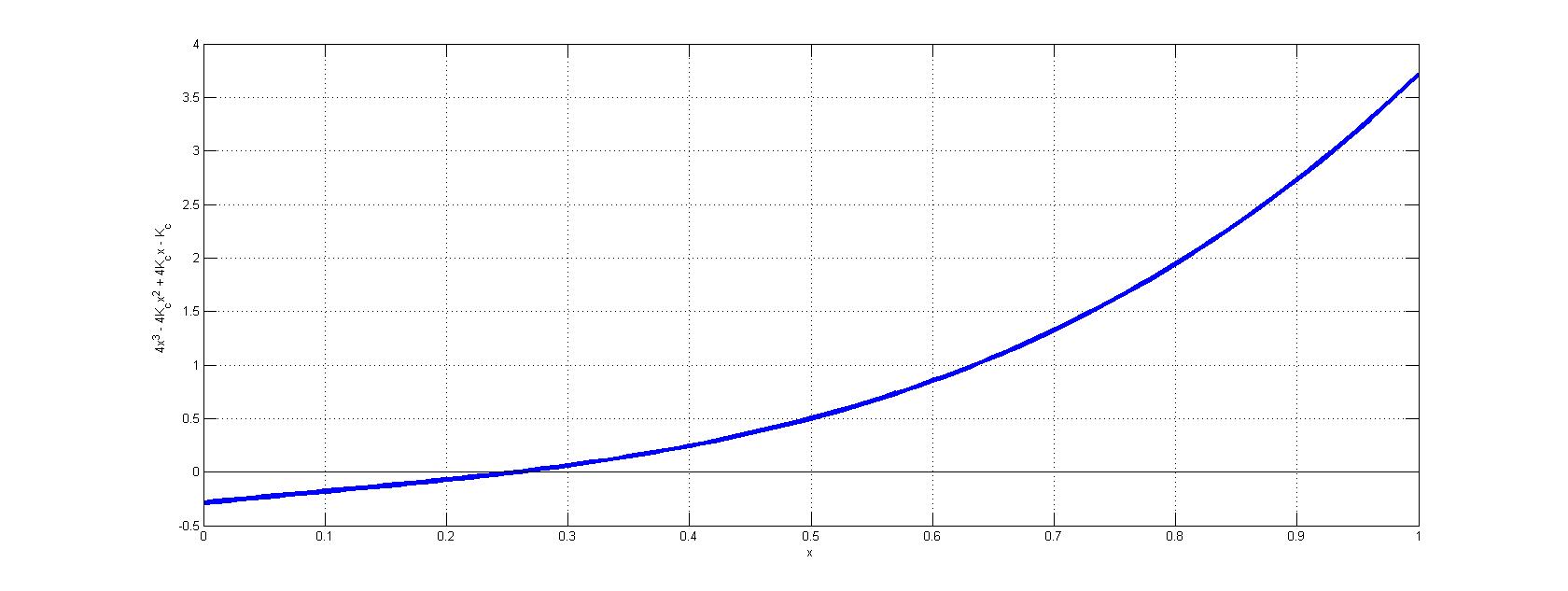 .
.
From this graph, is clear that \(x \approx 0.2571\), which is decently far off from the crude approximation in equation 5.
Q14.71
Use Le Chatelier’s Principal to explain what happens to the following reaction when you increase the temperature. Why does this happen?
N2(g) + 3 H2(g) ↔ 2 NH3(g) ΔH = −92kJ/mol
S14.71
Increasing the temperature will cause the equilibrium to shift towards the reactants (left). This is because the reaction is exothermic and releases heat. So if you add heat, more N2(g) and H2(g) will be created and balance out the reaction.
http://chemwiki.ucdavis.edu/Physical_Chemistry/Chemical_Equilibrium/Le_Chatelier's_Principle
Q14.84
For the synthesis of ammonia at 500 K,
\[N_2(g) + 3H_2 \rightleftharpoons 2NH_3(g)\]
with \(K_p = 11.08 \times 10^{-2}\). Assume that \(N_2\) and \(H_2\) are mixed in the mole ratio 1:3 and that the total pressure is maintained at 1.00 atm. What is the mole percent \(NH_3\) at equilibrium? Hint: Use this equation → Kp = ((XNH3)2/(XN2)(XH2)2 ) x (1/(Ptot)2)
S14.84
11.08 x 10^-2 = ((XNH3)2/(1)(3)2 x (1/1)2)
XNH3 = .998 mol
0.998 mol NH3/6 tot mol x100 = 16.63% mol NH3
Q14.29
Consider a mixture of 2.7 mol O2, 3.2 mol SO2, and 2.1 mol SO3. Can this mixture be maintained in a 7.2 L container where Kc=20?
Q14.31
In the reaction 2ClO2(g)+O2(g)<-->2ClO3(g), 0.241 mol ClO2, 0.197 mol O2, 0.670 mol ClO3 are simultaneously placed into a 1.7 L vessel at a temperature of 1000K.
- If Kc=2.53E2 is the mixture at equilibrium?
- If it is not in equilibrium then in what direction will the reaction shift?
Q14.33
Consider a mixture of 0.263 mol H2, and .263 mol Br2that is broughtto equilibrium at 500 degrees Celsius in a 4.0 L flask. What are concentrations at equilibrium of H2, Br2, and HBr?
Q14.35
For the reversible reaction between \(CO\) and \(CO_2\) in the gas phase
\[CO(g)+O_2(g) \rightleftharpoons CO_2(g)\]
If 0.352 mol of \(CO\) were added to 0.067 mol of \(CO_2\) in a 3 L flask at 668 K, how many moles of \(O_2(g)\) will be present at equilibrium? The \(K_c\) of this reaction is \(1.2 \times 10^3\) at 668 K.
Q14.37
Equilibrium is reached in a 2.5 L flask at 800 °C for the reaction of
\[CaCO_3(s) \rightleftharpoons CaCO(s)+ CO_2(g)\]
with \(K_c=2.68 \times 10^{-3}\)
- How many moles of \(CaCO_3(s)\) is present at equilibrium if 0.715 mols \(CaCO_3(g)\) is introduced into an empty flask?
Q14.39
Consider the reaction,Ca(OH)2 + 2 CH3COOH= Ca(CH3COO)2 + 2H2O ; Kc=4.0
A reaction occurs in a mixture of 19.3 g Ca(OH)2, 21.7 g CH3COOH, 41.2 g Ca(CH3COO)2, and 70.1 g H2O.
- In what direction will the reaction proced?
- How many grams of each will be present at equilibrium?
Q14.41
Given, the thermal decomposition of CaCO3(g) → CaO(g) + CO2(g); Kc=4.84 @300K
if 0.362 mol CaCO3 dissociatesin a 2.47 L flask at 300 K what will be the TOTAL Pressure at equilibrium?
Q14.43
write the equilibrium expression for the reaction [citrate(aq)]=.0027 M, [aconitate(aq)]=4.31E-5, and [H2O]= 53.6M. Determine whether the reaction is at equilibrium / or which direction it will proceed if not at equilibrium.
Citrate(aq)ßàaconitate(aq)+H2O(l) K=0.031
Q14.45
Based on the equation HNO3 (aq) --> H+ (aq) + NO3- (aq) ; K=3.21E11, if 2.0 M HNO3 is added to a .5 L flask then what are the resulting ion concentrations at equilibrium?
Q14.53
Based on the following equilibrium reaction 2H(g)+O(g)ßàH2O(g) ; K=35
What is the partial pressure of Oxygen?
Q14.55
Given the following situations, determine what will happen to the amount of H2that will be present in an equilibrium mixture in the reaction 3Fe(s)+4H2O(g)<-->Fe3O4(s)+4H2(g) ; ∆H˚=-150 kJ
- Decreasing the temperature of the mixture
- Introducing more Fe(s)
- Halving the volume of the container
- Adding a catalyst
63
Consider the reaction 4H2(g)+2O2(g)<-->2H2O(g) ∆H˚=271 kJ
what affect does decreasing the temperature have on
- The equilibrium production of NO(g)
- The rate at which the reaction takes place
Q14.65
Based on the reaction N2(g)+O2(g)<-->2NO(g) what will happen to the Pressure of N2 if the volume of the mixture were to be increased by decreasing the pressure by half?
Q14.71
A container of NOg) at 0.96 atm is brought into contact with 100 mL of a saturated aqueous solution with a NO2 concentration of 5.53E-2 M. If the container is 1100 ml in volume at 30˚C, then a) what will be Kc for the equilibrium? And b) If .023 mol of 250NO is added to the flask, then how many moles of 14CO2 (g) will form in the aqueous solution?
Q14.73
for the reaction V3+(aq)+Cr2+(aq)<-->V2+(aq)+Cr3+(aq) (Kc=7.2E2) with initial concentrations [V3+]=[Cr2+]=.0231 M and[V2+]=[Cr3+]=.260 M, what happens to the concentrations if the volume of the solution, 1L, is diluted to 2L with water?
Q14.75
Given the following generic reaction at 670 K what will be the total pressure at equilibrium if one starts with gas A at 0.837 atm?
\[2A(g) \rightleftharpoons 2B(g)+C(g)\]
with \(K_p=1.3 \times 10^{-4}\)
Q14.77
Calculate the equilibrium amounts of the previous equation 2A<-->2B+C with a Kc= 1.5E2 if the initial [A]= 1.3 M.
Q14.79
based on the reaction 2SO2(g)+O2(g)<-->2SO3(g) ∆H<0 , explain how each of the following will affect the amount of SO3(g)
- Increase pressure
- Increase temperature
- Increase the amount of O2(g)
Q14.84
what will be the molar mass of the resulting gaseous mixture in the reaction COCl2(g)<-->CO(g)+Cl2(g) given that Kp=4.44E-2 @122K and \(P_{tot}=2.5\,atm\)?
Q14.102
given the following equilibrium equation, A+B<-->C with equal concentrations of A and C and a Kc=1000, what must the concentration of C be at equilibrium?
Q14.104
For the reaction \[2SO_2(g)+O_2(g) \rightletharpoons 2SO_3(g)\] with \(K_p= 1.37 \times 10^{-2}\) at 1500˚C. What do you expect the relationship to be between \(K_c\) and \(K_p\)?
SolutionS
1) a) H20 <-->H++OH- ; kc=[H+][OH-]
b) Co(l)+NO2(l)<--> NO(l)+CO2(l) ; kc=[NO][CO2]/[CO][NO2]
c) HI(g)+H20(l) <-->H30+(aq)+I-(aq) ; kc=[H30+][I-]/[HI]
2) a) 1N2(g)+ 3H2(g)<-->2NH3(g) Kp= P2(NH3)/P(N2)P3(H2)
b) CaCO3 <--> CaO(s) + CO2(g) Kp= P(CO2)
c) CO2(g) + NaOH(aq)<-->NaHCO3(aq) Kp= [NaHCO3]/P(CO2)[NaOH]
3) a) Kc= [HIO2]2/[HI]2[O2]
b) Kc= [NO2][ClNO]/[ClNO2][NO]
c) Kc= [HI]2/[H2][I2]
29) 2SO2(g) + O2(g)<--> 2SO3(g)
Kc=20=(2.1/7.2)/((2.7/7.2)*(3.2/7.2))=1.75<Kc=20
Therefore the mixture cannot be maintained indefinitely.
30) The reaction will proceed towards the products because Kc is much greater than one.
31)
a) Kc=2.53E2= (.67 mol/1.7 L)/((.241 mol/1.7 L)*(.197 mol/1.7 L)) = 23.99
23.99 is not equal to 2.53E2, therefor it is not at equilibrium.
b) Kc>Q therefore there will be a shift to the right, towards the products.
33) H2(g)+Br2(g)<-->2HBr(g) Kc=50.2 @ 500 degrees C
[]I .263 .263 0
[]c -x -x +2x
[]e .263-x .263-x 0+2x 50.2= ((2x/4 L)2)/((.263-x/4 L)2)
x= .205
[H2]eq=.263-.205= .058 M
[Br2]eq=.263-.205= .058 M
[HBr]eq= 0+ .205 = .205 M
35) CO(g)+O2(g)<-->CO2(g) Kc=1.2*103
[]I .352 0 .067
[]c +x +x -x
[]e .352+x x .067-x
Kc= 1.2E3=((.067-x/3L)/((.352+x/3 L)(x/3L))
X=5.15E-4= mols O2
37)
a) CaCO3(g)<-->CaCO(g)+ CO2(g) Kc=3.8E-2
[]I .731 .731 0
[]c -x +x +x
[]e .731-x .731+x x
Kc=3.8E-2=((x/2.5L)(.731+x/2.5L))/(.731-x/2.5L)
X=.268
n(CaCO3)=.731-.268=.463 mols
n((CaCO)=.731+.268=.999 mols
n(CO2)= x = .268 mols
b) CaCO3(g)<-->CaCO(g)+ CO2(g) Kc=3.8E-2
[]I .715 0 0
[]c -x +x +x
[]e .715-x x x
Kc=3.8E-2=(x2/2.5L)/(.715-x/2.5L)
X= .147
n(CaCO3)=.715-.147=..568 mols
n((CaCO=.x= .147 mols
n(CO2)= x = .147 mols
39)Ca(OH)2 + 2 CH3COOH= Ca(CH3COO)2 + 2H2O ; Kc=4.0
a)
n(Ca(OH)2)= 19.3g/74.093 g/mol=0.260 mols
n(CH3COOH)=21.7g/60.05 g/mol=.361 mols
n(Ca(CH3COO)2)=41.2/158.1669 g/mol=.260 mols
n(H2O)=70.1/18.02 g/mol=3.89 mol
Qc=((.260)(3.89))/((.361)(.260))= 10.78
Kc=4.0<10.78=Qc
Therefore the reaction will proceed to the left, towards reactants.
b)
Ca(OH)2 + 2 CH3COOH= Ca(CH3COO)2 + 2H2O ; Kc=4.0
[]I .260 .361 .260 3.89
[]c +x +2x -x -2x
[]e .26+x .361+2x .26-x 3.89-2x
Kc=4.0=((.26-x)(3.89-2x))/((.26+x)(.361+2x))
X=0.184
Mass(Ca(OH)2)=.260+.184=.444(74.093)=32.9 g
Mass(CH3COOH)=.361+2(.184)=.729(60.05)=43.77 g
Mass(Ca(CH3COO)2)=.26-.184=.076(158.1669)=12.02 g
Mass(H2O)=3.89-2(.184)=3.522(18.02)=63.47 g
41) CaCO3(g) → CaO(g) + CO2(g); Kc=4.84
[]e .146-x x x
Kc=4.84=(x2)/(.146-x)
X= .142
Equilibrium concentrations..
[CaCO3]= .146-.142=0.004 M
[CaO]= .142 M
[CO2]= .142 M
Mtot=.288
Ptot=(.288)(.08206)(300)=7.1
43)
Q=(4.31E-5)/.00217)=.0199
K>Q and therefore the reaction will proceed to the left (Not in initially in equilibrium)
45)
HNO3 is a strong acid and therefore dissociates into its ions completely. Hence the ion concentrations at equilibrium are [H+]=2M=[NO3-]
53)
P(O)= nRT/V=1mol x .08206 L atm mol-1K-1 atm x 600 K/1 =49.2 atm
55)
a) Decreasing the temperature of the mixture
-Because the reaction is exothermic heat can be thought of as a product and therefore, if the temperature decreases, then the amount of H2O(g) will increase.
b) Introducing more Fe(s)
-There should be no change in the amount of H2(g)
c) Halving the volume of the container (increasing pressure)
-This will cause a shift from the side with the most moles of gas to the side with the least moles of gas. IN this case they are the same so there will be no change.
d) Adding a catalyst
-No change, catalysts only affect the speed at which the reaction occurs).
63)
a) Less H2O(g) formed at lower temperatures
b) The rate of the reaction slows with the decrease in temperature
65) The equilibrium will shift to the side with the most mols and therefore P(N2) should increase.
71)
a) [NO]=n/v=P/RT= .96/.0862*303=.039 M Kc=5.53E-2/.039 =1.418
NO(g)<-->NO(aq) Kc=1.418=((5.53E-2+x)/.1L)/((.062-x)/1L)
[]I .039 5.53E-2 x=.0029
+.023 -----
[]c -x +x
[]e (.062-x) 5.53E-2+x total mols (NO(g))=(1L)(.0591)=.0591 mol
total mols(NO(aq)=(.1L)(.0582)=.00582 mol
250NO mol fraction= .01/.06492 x100= 15.4%=.154
mols 250NO(g)=(.0591)(.154)=.0091
mols 250NO(aq)=(.00582)(.154)= 8.96E-
Q14.73
The redox reaction in solution
\[V^{3+}(aq)+Cr^{2+}(aq) \rightleftharpoons V^{2+}(aq)+Cr^{3+}(aq)\]
has an equilibrium constant of \(K_c=7.2 \times 10^{2}\). If the reaction were initiated with with initial concentrations \([V^{3+}]=[Cr^{2+}]=0.0231\, M\) and \([V^{2+}]=[Cr^{3+}]=0.260\, M\), what happens to the concentrations if the volume of the solution, 1L, is diluted to 1.5L with water?
Equation: V3+(aq)+Cr2+(aq)<-->V2+(aq)+Cr3+(aq) (Kc=7.2E2)
Equilib: .0231 .0231 .260 .260
Dilution: .01155 .01155 .13 .13
Change: -x -x +x +x
New eq: .01155-x .01155-x .13+x .13+x
7.2E2= (.13+x)2/(.01155-x)2
x=.0065
new concentrations :
[V3+]=[Cr2+]=.0231-.0065=.0166
V2+]=[Cr3+]=.260+.0065=.2665
Q14.75
\[2A(g)<-->2B(g)+C(g) \]
\[Kp=1.3E-4\]
[]I .837 0 0
[]c -2x +2x +x
[]e (.837-2x) 2x x
Kp=1.3E-4=((2x)2(x))/(.837-2x)2
X=.8365 atm
Ptot= P(A)+P(B)+P(C)=(.837-2(.8365))+(2(.8365))+(.8365)=3.91atm
77) 2Aßà2B+C Kc= 1.5E2 [A]= 1.3 M
[]I 1.3 M 0 0
[]c -2x +2x +x
[]e 1.3-2x 2x x
Kc=1.5E-2=(2x)2(x)/(1.3-2x)2
X=.185
Equilibrium concentrations:
[A]=1.3-.185= 1.115 M
[B]=2(.185)= .37 M
[C]=.185 M
Q14.79
a) Increase pressure
-more SO3 will be produced
b) Increase temperature
-SO3 is reduced because heat is treated as a product in exothermic reactions
c) Increase the amount of O2(g)
-more SO3 will be produced in order to use up the excess oxygen
84)
COCl2(g)<-->CO(g)+Cl2(g) given that Kp=4.44E-2 @122K
[]I P 0 0
[]c -x +x +x
[]e P-x x x
Kp=4.44E-2=(x*x)/(2.5-2x)
X=.292
Ptot=2.5 atm= P-x+x+x=P+x
P=2.5-x
P(COCL2)=2.5-2x=1.916 atm
P(CO)=P(CL2)=.292atm
Mavg= (P(CO)*M(CO)/Ptot)+(P(Cl2)*M(Cl2)/Ptot)+(P(COCl2)*M(COCl2)/Ptot)=
Mavg= 87.36 g/mol
Q102
A+BßàC Kc=1000, what must the concentration of C be at equilibrium?
K=[C]2/[A]2[B] =1000
[B]=1/1000=.001 M
104) because Kp=Kc(RT)∆n we can determine that Kp>Kc
Q1
Based on these descriptions, write a balanced equation and the corresponding expression for each reversible reaction.
- Carbonyl fluoride decomposes into gaseous carbon dioxide and gaseous carbon tetra fluoride.
- Copper metal displaces silver (I) ion from aqueous solution, producing silver metal and an aqueous solution of copper (II) ion.
- Peroxodisulfate ion oxidizes iron (II) ion to iron (III) ion in aqueous solution and is itself reduced to sulfate ion.
Q2
Based on these descriptions, write a balanced equation and the corresponding Kp expression for each reversible reaction.
- Oxygen gas oxidizes gaseous ammonia to gaseous nitrogen and water vapor.
- Hydrogen gas reduces gaseous nitrogen dioxide to gaseous ammonia and water vapor.
- Nitrogen gas reacts with the solid sodium carbon- ate and carbon to produce solid sodium cyanide and carbon monoxide gas.
Q3
Write equilibrium constant expressions, \(K_c\), for the reactions.
Q29
Can a mixture of 2.2 mol O2, 3.6 mol SO2, and 1.8 mol SO3 be maintained indefinitely in a 7.2 L flask at a temperature at which Kc = 100 in this reaction?
Q30
Is a mixture of 0.0205 mol NO2 (g) and 0.750 mol N2O4 (g) in a 5.25 L flask at 25 °C, at equilibrium? If not, in which direction will the reaction proceed toward products or reactants?
Q31
In the reaction 2 SO2(g) + O2 (g) à 2 SO3(g), 0.455 mol SO2, 0.183 mol O2, and 0.568 mol SO3 are introduced simultaneously into a 1.90 L vessel at 1000 K.
- If Kc = 2.8 * 102, is this mixture at equilibrium?
- If not, in which direction will a net change occur?
Q33
A mixture consisting of 0.150 mol H2 and 0.150 mol I2 is brought to equilibrium at 445 °C, in a 3.25 L flask. What are the equilibrium amounts of H2, I2, and HI?
Q35
Starting with 0.3500 mol CO (g) and 0.05500 mol COCl2 (g) in a 3.050 L flask at 668 K, how many moles of Cl2 (g) will be present at equilibrium?
Q37
Equilibrium is established in a 2.50 L flask at 250 degrees Celsius for the reaction
\[PCl_5(g) \rightleftharpoons PCl_3(g) + Cl_2 (g)\]
with \(K_c = 3.8 \times 10^{-2}\). How many moles of \(PCl_5\), \(PCl_3\), and \(Cl_2\) are present at equilibrium, if
- 0.550 mol each of \(PCl_5\) and \(PCl_3\) are initially introduced into the flask?
- 0.610 mol \(PCl_5\) alone is introduced into the flask?
Q39
In the following reaction, kc=4.0.
C2H5OH+CH3COOH==CH3COOC2H5+H2O
A reaction is allowed to occur in a mixture of 17.2 g C2H5OH, 23.8 g CH3COOH, 48.6 g CH3COOC2H5, and 71.2 g H2O.
- In what direction will a net change occur?
- How many grams of each substance will be present at equilibrium?
Q41
Formamide, used in the manufacture of pharmaceuticals, dyes, and agricultural chemicals, decomposes at high temperatures.
\[HCONH_2 (g) \rightleftharpoons NH_3 (g) + CO (g)\]
Kc = 4.84 at 400 K
If 0.186 mol HCONH2(g) dissociates in a 2.16 L flask at 400 K, what will be the total pressure at equilibrium?
Q43
Cadmium metal is added to 0.350 L of an aqueous solution in which [Cr3+] = 1.00 M. What are the concentrations of the different ionic species at equilibrium? What is the minimum mass of cadmium metal required to establish this equilibrium?
Q45
One sketch below represents an initial non-equilibrium mixture in the reversible reaction
SO2 (g) + Cl2 (g) == SO2Cl2 (g)
Kc = 4.0
Which of the other three sketches best represents an equilibrium mixture? Explain.
Q53
1.00 mol each of CO and Cl2 are introduced into an evacuated 1.75 L flask and the following equilibrium is established at 668 K.
CO (g) + Cl2 (g) à COCl2 (g)
Kp = 22.5
For this equilibrium, calculate (a) the partial pressure of COCl2 (g); (b) the total gas pressure.
Q55
Continuous removal of one of the products of a chemical reaction has the effect of causing the reaction to go to completion. Explain this fact in terms of Le Chatelier’s principle.
63
What effect does increasing the volume of the system have on the equilibrium condition in each of the following reactions?
Q71
Explain why the percent of molecules that dissociate into atoms in reactions of the type I2(g) == 2I (g) always increases with an increase in temperature.
Q73
Refer to Example 15-13. Suppose that 0.100 L of the equilibrium mixture is diluted to 0.250 L with water. What will be the new concentrations when equilibrium is re-established?
Q75
Starting with SO3 (g) at 1.00 atm, what will be the total pressure when equilibrium is reached in the following reaction at 700 K?
77
Derive, by calculation, the equilibrium amounts of SO2, O2, and SO3 listed in (a) Figure 15-6(c); (b) Figure 15-7(b).
79
One of the key reactions in the gasification of coal is the methanation reaction, in which methane is produced from synthesis gas a mixture of \(\ce{CO}\) and \(\ce{H2}\).
\[\ce{CO (g) + 3H2 (g) <=> CH4 (g) + H2O (g)} \nonumber\]
\(\Delta{H} = - 230 kJ\) and \(K_c = 190\) at 1000 K
- Is the equilibrium conversion of synthesis gas to methane favored at higher or lower temperatures? Higher or lower pressures?
- Assume you have 4.00 mol of synthesis gas with a 3:1 mol ratio of \(\ce{H_2 (g)}\) to \(\ce{CO (g)}\) in a 15.0 L flask. What will be the mole fraction of \(\ce{CH4 (g)}\) at equilibrium at 1000 K?
84.
For the synthesis of ammonia at 500 K,
\[N_2(g) + 3H_2 (g) \rightleftharpoons 2NH_3(g)\]
with \(K_p = 9.06 \times 10^{-2}\). Assume that \(N_2\) and \(H_2\) are mixed in the molar ratio of \(1:3\) in a \(1\) liter flask, respectively and that the total pressure is maintained at 1.00 atm. What is the mole percent \(NH_3\) at equilibrium?
102.
Equilibrium is established in the reaction \(2SO_2 (g) +O_2 (g) \rightleftharpoons 2SO_3 (g)\) at a temperature where Kc = 100. If the number of moles of SO3 (g) in the equilibrium mixture is the same as the number of moles of SO2 (g), (a) the number of moles of O2 (g) is also equal to the number of moles of SO2 (g); (b) the number of moles of O2 (g) is half the number of moles of SO2; (c) [O2] may have any of several values; (d) [O2] = 0.010 M.
104.
For the reaction
\[(2 NO_2 (g) \rightleftharpoons 2NO (g) + O_2 (g)\]
\(K_c = 1.8 \times 10^{-6}\) at 184 °C.
At 184 °C, the value of \(K_c\) for the reaction
\[NO (g) + 3/2 O_2 (g) \rightleftharpoons NO_2 (g)\]
is:
- 0.9 * 106;
- 7.5 * 102;
- 5.6 * 105;
- 2.8 * 105.
Solutions
S1
S2
Video Solution
S3
29. Cannot be maintained indefinitely in a 7.2L flask.
30. Shift forward to products.
31. No. Forward to product.
33. I2: 0.0330mol
HI: 0.234mol
35. 4.0*10-4 mol
37. (a) PCl3: 0.623mol
PCl5: 0.478mol
(b) PCl3: 0.20mol
PCl5 0.41mol
39. (a) towards left
(b) 68g
41. 5.58atm
43. 10.1g
45. b
53. (a) 30.14 atm
(b) 32.4 atm
55. Continuous removal of the product of a chemical reaction has the effect of causing the reaction to go to completion that is which makes Q less than K and reaction shift the right as result and change in pressure of a constant temperature equilibrium mixture.
63. (a) Volume
(b) No effect
(c) More reactions
71. The percent of molecules that dissociates into atoms on reaction of the I2 and 2I (g) always increase in temperature.
73. 2.98
75. 1.016 atm
S77.
- 0.27
- 0.085mol
S79
- Video Solution (Part A)
- Video Solution (Part B)
- low temperatures and high pressures favor conversation of synthesis gas to methane.
- 0.134
S84
28.06%
102
d
104. 750 (b)
1
Write a balanced equation that describes sodium chloride splits into Sodium and Chloride Ions.
\[NaCl \rightarrow Na^+ + Cl^-\]
2
Write a balanced equation that describes the decomposition of Hydrochloric Acid into its Ions.
\[HCl \rightarrow H^+ + Cl^-\]
3
Write equilibrium constant expressions, \(K_c\), for the reactions
- \(C +2H_2 \rightleftharpoons CH_4\)
- \(2Na + Cl_2 \rightleftharpoons 2NaCl \)
- \(NaHCO_3 \rightleftharpoons Na + HCO_3\)
S3
(a) Kc= [CH4]/[H2]2
(b)Kc= [NaCl]2/[Cl2]
(c) Kc=[HCO3]/[NaHCO3]
29.
There are two gases in a 4.5 L vessel. The mass of C6H16 is 6.68g and the mass of C3H8is 2.28g. What is the value of Kc for this reaction.
S29
Mol C6H16= 6.68g (1mol C6H16/88.22g C6H16)=0.0757mol
[C6H16]=0.0757mol/4.5L=0.0168M
Mol C3H8= 2.28g C3H8 x 1 mol C3H8/44.11g C3H8=0.0517mol
[C3H8]= 0.0517/4.5L= 0.0115M
Kc=[C3H8]/[C6H16]= (0.0115)/(0.0168)=0.685
30.
Is a mixture of 1.30 L of water and 3.15 mol of HCN and .001 mol of CN- in equilibrium? If not, in which direction will the shift proceed, towards products or reactants?
S30
(Ka (HCN) = 6.2e-10)
[HCN] = 3.15 mol / 1.30 L = 2.42 M [CN-] = [H+] = 7.69e-4 M
Q = [CN-] * [H+] / [HCN] = (7.69e-4)^2 / (2.42) = 2.45e-7
Q>K... therefore... reaction shifts left, towards the reactants.
31.
For the reaction in equilibrium,
\[H_2SO_4 + H_2O \rightleftharpoons HSO_4^- + H_3O^+\]
if the \(K_a\) value for \(H_2SO_4\) is \(2.42 \times 10^{-5}\), the molar concentration of \(H_2SO_4\) is 0.056 M, and the pH of the solution is 4.5, what is the concentration of \(HSO_4^-\)?
S31
[H3O+] = 10^-4.5 = 3.16e-5 M
2.42e-5 = [HSO4-] * (3.16e-5) / (.056)
[HSO4-] = .0429 M
33
In an exothermic reaction increasing the temperature shifts the equilibrium in which direction?
S33
Left, more heat is more products so it shifts towards reactants.
35
If the number of moles remains constant, a change in volume does what to the equilibrium of a system?
S35
Nothing, Keq also remains constant.
37
Using the above equilibrium reaction at 25 degrees Celsius with \(K_c= 7.1 \times 10^2\)
\[H_2 (g) + I_2 (g) \rightleftharpoons 2 HI (g)\]
- find the molarity of \(HI\), assuming an equilibrium concentration of 0.76 M \(I_2\), and 0.32 M \(H_2\)
- find the molarity of \(I_2\), assuming an equilibrium concentration of 2.36 M \(HI\), and 0.42 M \(H_2\)
S37
a) Kc= [HI]^2 / [I2] x [H2]
7.1 x 10^2 = [HI]^2 / (.76 M x .32 M)
=13.14 M HI
b) Kc= [HI]^2 / [I2] x [H2]
7.1 x 10^2= (2.36M)^2 / (.42) x [I2]
(2.36M)^2 / ((.42) x (7.1 x 10^2) = [I2]
=0.018 M I2
39
In the following equilibrium reaction, \(K_p = 3.16\):
\[2 PO_4 \rightleftharpoons 2 PO_3 + O_2\]
A reaction occurs at 273 K in a 1.0 L container with 4.56 g of \(PO_4\), 6.54 g of 2 \(PO_3\) and 1.32 g of \(O_2\).
- In what direction will a net change occur?;
- What will be the partial pressures of each substance at equilibrium?
S39
A)
n = (4.56 g PO4)(1 mol / 94.97 g) = 0.0480 mol PO4
n = (6.54 g PO3)(1 mol / 78.97 g) = .0828 mol PO3
n = (1.32 g O2)(1 mol / 32 g) = .0413 mol O2
PV=nRT
PPO4 = (.0480 mol)(.08206)(273 K) / (1.0 L) = 1.08 atm
PPO3 = (.0828 mol)(.08206)(273 K) / (1.0 L) = 1.85 atm
PO2 = (.0413 mol)(.08206)(273 K) / (1.0 L) = .925 atm
Q = (1.85)^2 * (.925) / (1.08)^2 = 2.71
2.71<3.16... Q<K... therefore... reaction shifts right, towards products.
B)
K = 3.16 = (1.85 + 2x)^2 * (.925+x) / (1.08 – 2x)^2
x = 0.0218
PPO4 = 1.08 – 2(.0218) = 1.04 atm
PPO3 = 1.85 + 2(.0218) = 1.89 atm
PO2 = .925 + .0218 = .947 atm
41.
Dinitrogen tetroxide, (\(N_2O_4\)) in combination with specific forms of hydrazine can burn on contact without a separate ignition source, make it popular as a component of rocket fuel. At high temperatures the equilibrium is:
\[N_2O_4 \rightleftharpoons 2 NO_2\]
What are the partial pressures at equilibrium at 83 Celsius and 1.1 atm, if the density of the two equilibrium products is 2.44 g/l?
S41
Knowns:
- p=1.1atm
- W= average molar mass = ?
- R= .08206 atm-L/mol-K
- T= 83+273K = 356K
Using the periodic table:
- N2O4 is 92 g/mol
- NO2 is 46 g/mol
Calculations:
p * W = density * RT
1.1 atm *W = (2.44 g/L) * (.08206 atm-L/mol-K) * (356K)
W = 64.8 g/mol
If X is the mol fraction of N2O4, then 1 - X is the mol fraction of NO2
92 g/mol * X + 46 g/mol * (1-X) = 64.8 g/mol
X = .4087
and
1-X = .5913
p(N2O4) = 0.4087 *1.1atm = .4496 atm
p(NO2) = 0.5913*1.1atm = .6504 atm
Therefore, the partial pressure of N2O4 is .4496 atm and the partial pressure of NO2 is .6504 atm.
43
What will a catalyst do to the composition of an equilibrium mixture?
Nothing, catalysts effect time, but once at equilibrium a system won’t take effect to a catalyst.
45.
For the reaction
\[H_2(g) + I_2(g) \rightleftharpoons 2 HI(g)\]
Kc = 50.3 at 731 K. Equal amounts (1.00 M each of the three components) are added to a beaker, and then the temperature is raised to 731 K.
Calculate the equilibrium concentrations.
S45
H2(g) + I2(g) = 2 HI(g)
1.00 1.00 1.00 initial concentration
-x -x 2x amount of change
1-x 1-x 1+2x equilibrium concentration
Kc=50.3 = [HI]2/[H2][I2] = (1+2x)2/(1-x)(1-x)
Therefore (1+4x+4x2)= 50.3*(1-2x-x2)=50.3-100.6x-50.3x2
-46.3x2+104.6x - 49.3 = 0
Solving the quadratic equation: The roots are: 1.589 and .670
Since x cannot be greater than 1, the only solution is x = .670.
Therefore, the equilibrium concentrations are:
[H2] = 1-.670 = .33
[I2] = 1-.670 = .33
[HI] = 1+2*.670 = 2.34
53
Determine the partial pressure of the Hydrogen in the following reaction held within a 2L flask
\[H^+ + Br^- \rightleftharpoons HBr\]
P[Br] = (nRT)/((V)) = ((1mol)(0.08206)*(668K)/(2L) = 27.4atm
55.
What is Le Chatelier’s principle?
Answer:
Le Chatelier’s principle is when a new equilibrium has occurred due to a chance of change in temperature or pressure on a chemical equilibrium. It can be known as the Equilibrium Law.
63
What affect does decreasing the volume of the system have on the equilibrium condition in each of the following reactions:
- \(2 H_2(g) + C (s) \rightleftharpoons CH_4(g)\)
- \(2 CO_2 (g) \rightleftharpoons 2 CO (g)+ O_2 (g)\)
- \(2 N_2O (g) + O_2 (g) \rightleftharpoons 4 NO (g)\)
S63
- shifts right
- shifts left
- shifts left
65
Hb(aq) + O2(aq) àHb:O2(aq) ∆H<0
How does decreasing temperature effect this system?
S65
Because the reaction is endothermic, we know that decreasing the temperature adds more to the reactants side, shifting the equilibrium towards the products.
69.
The standard enthalpy of reaction for the combustion of ethanol is 1,418kJ/mole. Write the equation:
\[C_2H_5OH(l) + 3O_2 (g) \rightleftharpoons 2CO_2 (g)+ 3H_2O(l)\]
How does pressure affect the equilibrium?
As 3 molecules of O2 give 2 molecules of CO2, increasing pressure drives the equilibrium to the right side of the reaction, as well as decrease the volume and increase the number of moles.
# 77
In a reversible reaction,
\[2Na + Cl_2 \rightleftharpoons 2NaCl\]
initial conditions indicate 2 mol \(Na\) and 1 mol \(Cl_2\). What is the expected amount of NaCl at equilibrium?
Less than 2mols, because the \(Cl_2\) is the limiting reagent at 1mol, but the theoredical yield of NaCl is 2mols, so it can never hit that point unless more Cl is added.
79.
One of the key reactions in the gasification of coal is the ethanation reaction, in which ethane is produced from synthesis gas – a mixture of CO and H2.
2CO(g) + 2H2(g) àßC2H4(g) + 2H2O (g)
DH= - 230 kJ; Kc= 178 at 1200K
- Is the equilibrium conversion of synthesis gas to methane favored at higher or lower temperatures? Higher or lower pressures? Products are favored with higher temperatures and lower pressures.
90.
Consider the following reaction:
\[PCl_3(g) + Cl_2(g) \rightleftharpoons PCl_5(g)\]
An equilibrium mixture at 345 Kelvin in a 6.50 L vessel contains:
- 1.35 mol \(PCl_3\),
- 0.450 mol \(Cl_2\), and
- 3.20 mol \(PCl_5\).
The equilibrium constant for the reaction is \(K_p = 1.21\). If 0.50 mol of PCl5 are removed from the system, what will the pressures of each species be once the reaction returns to equilibrium?
S90
PV=nRT P = nRT / V
PPCl3 = (1.35 mol)(.08206)(345 K) / (6.50 L) = 5.88 atm
PCl2 = (.450 mol)(.08206)(345 K) / (6.50 L) = 1.96 atm
PPCl5= (3.20 mol)(.08206)(345 K) / (6.50 L) = 13.9 atm
PPCl5= (3.20 - 0.50 mol)(.08206)(345 K) / (6.50 L) = 11.8 atm
1.21 = (11.8 + x) / (5.88 – x)(1.96 – x) x = 0.210
PPCl3 = 5.88 – 0.210 = 5.67 atm
PCl2= 1.96 – 0.210 = 1.75 atm
PPCl5 = 11.8 + 0.210 = 12.01 atm
103.
For the oxidation of ethanol:
\[C_2H_5OH(l) + 3O_2 (g) \rightleftharpoons 2CO_2 (g)+ 3H_2O(l)\]
How does pressure affect the equilibrium?
S103
Answer: As 3 molecules of O2 give 2 molecules of CO2, increasing pressure drives the equilibrium to the right side of the equation, as well as decreasing the volume and the number of moles.
Q1
Based on these descriptions, write a balanced equation and the corresponding \(K_c\) expression for each reversible reaction:
- Sulfur trioxide, \(SO_{3 (g)}\), decomposes into gaseous oxygen and gaseous sulfur dioxide.
- Zinc metal displaces silver(I) ion from aqueous solution, producing silver mean and an aqueous solution of zinc(II) ion.
- Oxalate ion, \(C_2O_4^-\), oxidizes copper(I) ion to copper(II) ion in aqueous solution and is itself reduced to carbon dioxide.
Solution
a)
\[2 SO_{3 (g)} \rightleftharpoons O_{2 (g)}+2 SO_{2 (g)}\]
\[K_c= \dfrac{[SO_2]^2 [O_2]}{[SO_3]^2}\]
b)
\[Zn_{(s)}+ 2Ag^+_{(aq)} \rightleftharpoons 2Ag_{(s)} + Zn^{2+}_{(aq)}\]
\[K_c= \dfrac{[Zn^{2+}]}{[Ag^+]^2} \]
c)
\[C_2O^-_{4 (aq)} + 2Cu^+_{(aq)} \rightleftharpoons 2CO_{2 (aq)}+[(Cu)]^(2+)_{(aq)}\]
\[K_c= \dfrac{ [CO_2]^2 [Cu]^{2+}} {[C_2 O_4^-][Cu^+]^2}\]
Q2
Based on these descriptions, write a balanced equation and the corresponding \(K_p\) expression for each reversible reaction:
- \(KO_{2 (s)} + CO_{2 (g)} \rightleftharpoons KCO_3 + O_{2 (g)}\)
- \(HF_{ (aq)} + H_2 O_{(l)} \rightleftharpoons H_3O^+_{(aq)} + F^-_{(aq)}\)
- \(HCl_{ (g)} + I_{2 (g)} \rightleftharpoons HI_{(g)} + Cl_{2 (g)}\)
Solution
a)
\[4KO_{2 (s)} + 2CO_{2 (g)} \rightleftharpoons 2KCO_3 + 3O_{2 (g)}\]
\[K_c = \dfrac{[O_2]^3}{[CO_2]^2}\]
b)
\[ HF_{(aq)} + H_2O_{(l)} \rightleftharpoons H_3O^+_{(aq)} + F^-_{(aq)}\]
\[K_c = \dfrac{[H_3O^+][F^-]}{[HF]}\]
c)
\[2HCl_{(g)} + I_{2 (g)} \rightleftharpoons 2HI_{(g)} + Cl_{2 (g)}\]
\[K_c = \dfrac{[HI]^2 [Cl_2]}{[HCl]}\]
Q3
Write equilibrium constant expressions, \(K_c\), for the reactions:
- \(2CO_{(g)}+ O_{2(g)} \rightleftharpoons 2CO_{2 (g)}\)
- \(Fe^{2+}_{(aq)} + 2H_2O_{(l)} \rightleftharpoons FeOH^{2+}_{(aq)} + H_3O^+_{(aq)}\)
- \(HNO_{2 (aq)} + H_2O_{(l)} \rightleftharpoons H_3O^+_{(aq)} + NO^-_{2 (aq)}\)
Solutions
\[K_c = \dfrac{[CO_2]^2}{[CO]^2[O_2]}\]
\[K_c = \dfrac{[Fe(OH)][H_3O^+]}{[Fe^{3+}]}\]
\[ K_c = \dfrac{[H_3O^+][NO_2^-]}{[HNO_2]}\]
29
Can a mixture of 3.1 mol \(CO\), 3.9 mol \(O_2\), and 2.2 mol \(CO_2\) be maintained indefinitely in a \(9.2\; L\) container at a temperature at which \(K_c = 95\) in this reaction (and why or why not):
\[2CO_{(g)} + O_{2 (g)} \rightleftharpoons 2CO_{2 (g)}\]
Solution
Q_C = ([[([(CO)]_2])]^2)/([([CO})]^2 [O_2]) = (([((2.2 mol [(CO)]_2)/(9.2 L)))]^2)/(((3.1 mol CO )/(9.2 L))^2 ((3.9 mol O_2)/(9.2 L)) ) = 1.19
1.19 < K_c = 95. Thus the mixture described cannot be maintained indefinitely. Because Q_C < K_c, the reaction will proceed toward the products until the equilibrium is established.
30
Is a mixture of 0.0196 mol \(CO_{2 (g)}\) and a 0.815 mol \(C_2O_{4 (g)}\) in a 6.15 L flask at 30°C at equilibrium? If not, in which direction will the reaction proceed: toward the reactants or products?
\[ C_2O_{4 (g)} \rightleftharpoons 2 CO_{2 (g)}\]
with
\[K_c = 7.66 \times 10^{-5}\]
Solution
\[Q = \dfrac{[CO_{2(g)}]^2}{[C_2O_{4(g)}]}\]
\[ = \dfrac{ \left( \dfrac{0.0196\; mol \; CO_2 } {6.15\; L} \right) ^2}{\dfrac{0.815\; mol\; C_2O_4}{6.15\; L}} = 7.66 \times 10^{-5}\]
\(\therefore Q = K\)
The reaction is already at equilibrium.
31
In the reaction:
\[2H_{2(g)} + O_{2(g)} \rightleftharpoons 2H_2O_{(l)}\]
if 0.05 mol \(H_2\) and 0.02 mol \(O_2\), 20 mol of \(H_2O\) are introduced simultaneously into a 1.0 L vessel.
- If \(K_c= 1.4 \times 10^{83}\) is the mixture initially at equilibrium.
- If not, in which direction will a net change occur?
Solution
a)
\[K_c =\dfrac{1}{[H_{2(g)}]^2 [O_{2(g)}]} =1.4 \times 10^{83}\]
\[Q = \dfrac{ 1}{(0.05)^2(0.02)} = 4 \times 10^5\]
\( \therefore Q \neq K_c\)
The mixture is initially not at equilibrium.
b) The reaction will experience a net change in the direction of the products because since \(Q<K\).
33
A mixture consisting of 0.5 mol \(Cu^{2+}\) and 0.5 mol \(Sn^2+\) is brought to equilibrium in a 1 L flask. What is the equilibrium concentration of \(Sn^{4+}\). The reaction proceeds as follows:
\[2Cu^{2+}_{(aq)} + Sn^{2+}_{(aq)} \rightleftharpoons 2Cu^+ + Sn^{4+}\]
wth \(K_c= 1.48\)
Solution:
An ICE table is necessary to solve this problem.
| ICE | \(2Cu^{2+}_{(aq)}\) | \(Sn^{2+}_{(aq)}\) | \(\rightleftharpoons\) | \(2Cu^+\) | \(Sn^{4+}\) |
| Initial | 0.5 mol | 0.5 mol | 0 mol | 0 mol | |
| Change | -2x | -x | +2x | +x | |
| Equilibrium | 0.5 mol - 2x | 0.5 mol - x | +2x | +x |
\[ K_c = \dfrac{(x^2)(x)}{(0.5-2x)^2(0.5-x)} = 1.48\]
\[x=0.1752\]
\[ \therefore [Sn^{4+}]=0.1752\]
35
Starting with 0.5 mol of \(PCl_{5(g)}\) and 1 mol of \(Cl_{2(g)}\), in a 2.0 L flask, how many moles of \(PCl_{3(g)}\) will be present at equilibrium?
\[PCl_{5(g)} \rightleftharpoons PCl_{3(g)} + Cl_{2 (g)}\]
with
\[K_c= 3.8 \times10^{-2}\]
Solution:
Reaction is already balanced:
\[PCl_{5(g)} = PCl_{3(g)}+ Cl_{2 (g)}\]
An ICE table is necessary to solve this problem (constructed in terms of molarity, not mol).
| ICE | \(PCl_{5(g)}\) | \(\rightleftharpoons\) | \(PCl_{3(g)}\) | \(Cl_{2 (g)}\) |
| Initial | 0.25 mol | 0 mol | 0.5 mol | |
| Change | -x | +x | +x | |
| Equilibrium | 0.25 mol - x | +x | 0.5 mol +x |
\[ K_c = 3.8 \times 10^{-2}\]
\[3.8 \times 10^{-2} =\dfrac{x(0.5+x)}{0.25-x}\]
\[x =0.0335\]
\[\therefore [PCl_3]=0.0335\; M \]
37
Equilibrium is established in a 3.0 L flask for the following reaction.
\[2H_2S_{(g)}+ CH_{4(g)} \rightleftharpoons 4H_{2(g)} +Cs_{2(g)}\]
with
\[K_c=5.27 \times 10^{-8}\]
How many moles of \(CS_{2(g)}\) and \(CH_{4(g)}\) are present at equilibrium in the two initial situations:
- If 3 mol of \(H_2S_{(g)}\) and \(CH_{4(g)}\) are initially introduced into the flask.
- If 4 mol of \(4H_{2(g)}\) and \(CS_{2(g)}\) are initially introduced into the flask.
Solution:
The reaction is already balanced
\[2H_2S_{(g)}+ CH_{4(g)} \rightleftharpoons 4H_{2(g)} +CS_{2(g)}\]
Scenario A)
An ICE table is necessary to solve this problem.
| ICE | \(2H_2S_{(g)}\) | \(CH_{4(g)}\) | \(\rightleftharpoons\) | \(4H_{2(g)} \) | \(CS_{2(g)}\) |
| Initial | 1 M | 1 M | 0 M | 0 M | |
| Change | -x | -x | +x | +x | |
| Equilibrium | 1 M - 2x | 1 M - x | +x | +x |
\[5.27 \times 10^{-8} = \dfrac{(x^5)}{(1-x)^3\]
\(x= .0343= [CS_2]\]
\(1 - 0.0343 = 0.9657 = [CH_4]\]
Scenario B)
An ICE table is necessary to solve this problem.
| ICE | \(2H_2S_{(g)}\) | \(CH_{4(g)}\) | \(\rightleftharpoons\) | \(4H_{2(g)} \) | \(CS_{2(g)}\) |
| Initial | 0 | 0 | 4/3 M | 4/3 M | |
| Change | +x | +x | -x | -x | |
| Equilibrium | +x | +x | 4/3 M - x |
4/3 M - x |
\[ 5.27 \times 10^{-8} =\dfrac{(4/3-x)^5}{x^3}\]
\[x= 1.2925= [CH_4]\]
\[4/3 - 1.2925 = 0.04083 = [CS_2]\]
39
The following reaction occurs in the presence of 10 grams of \(CH_{4(g)}\), 15 grams of \(C_2H_{2(g)}\), and 2 grams of \(H_{2(g)}\).
\[2CH_{4(g)} \rightleftharpoons C_2H_{2(g)} + 3H_{2(g)}\]
with
\[K_c= 0.154\]
What direction will a net change occur and now many grams of each substance will be present at equilibrium?
Solution:
First one must find the moles of each substance.
- 10 grams \(CH_4\)/16 grams/mol \(CH_4\)= 0.625 mol \(CH_4\)
- 15 grams \(C_2H_2\)/26 grams/mol= 0.5769 mol \(C_2H_2\)
- 2 grams \(H_2\)/2 grams/mol= 1 mol \(H_2\)
\[Q=\dfrac{0.5769 X 1^3}{(0.625)^2}= 1.454 > 0.154\]
Since \(Q>K_c\), the reaction shifts to the left.
\[2CH_{4(g)} \rightleftharpoons C_2H_{2(g)} + 3H_{2(g)}\]
An ICE table is necessary to solve this problem (in terms of moles).
| ICE | \(2CH_{4(g)}\) | \(\rightleftharpoons\) | \(C_2H_{2(g)} \) | \(3H_{2(g)}\) |
| Initial | 0.625 | 0.5769 | 1 | |
| Change | +2x | -x | -3x | |
| Equilibrium | 0.625 + 2x | 0.5769 - x |
1 - 3x |
\[0.154=\dfrac{(0.5769-x)(1-x)^3}{(0.625+x)^3}\]
\(x= 0.277\)
- \([CH_4]= 0.625+0.277= 0.902\)
- \([C_2H_2]= 0.299\)
- \([H_2]= 0.722\)
41
Gaseous hydrogen iodide is placed in a closed container, where it partially decomposes.
\[ 2HI_{(g)} \rightleftharpoons H_{2 (g)} + I_{2 (g)}\]
with
\[ K_c = 5.5 \times 10^5 \; @ \; 698\;K\]
If 0.172 mol \(HI_{(g)}\) is initially added to a 1.67 L flask at 698 K, what will be the total partial pressure at equilibrium?
Solution
- \([HI]_i =\dfrac{0.172\; mol}{1.67\; L}=0.103\; M\)
An ICE table is necessary to solve this problem (in terms of mole).
| ICE | \(2HI_{(g)} \) | \(\rightleftharpoons\) | \(H_{2 (g)}\) | \(I_{2 (g)}\) |
| Initial | 0.172 M | 0 | 0 | |
| Change | -2x | +x | +x | |
| Equilibrium | 0.172 M - 2x | +x |
+x |
\[K_c= \dfrac{[H_2][I_2]}{[HI]^2}= \dfrac{x^2}{(0.172-x)^2}=5.5 \times 10^5\]
\[ x^2=94600-5.5 \times 10^5 x 0 = x^2 + 5.5 \times 10^5 (x-94600)\]
Solving the quadratic equation:
\[x= -5.5 \times 10)^5 \pm \sqrt{\dfrac{(3.03 \times 10^11) + 378400)}{2}}=227 M,-550227 M\]
[total] = [H2] + [I2] + [2HI] = x+x+ 0.172-x = 0.172 + 227 ≈ 227 M
Ptot = (227 mol)/L× (0.08206 L atm)/(mol K)× 698K=1.3 ×[(10)]^4 atm
55
The continuous removal of reactants of a chemical reaction has the effect of causing the reaction to go backwards. Explain this in terms of Le Châtlier’s principle.
Solution
Continuous removal of the reactants has the effect of decreasing the concentrations of the reactants below their equilibrium values. Therefore, the equilibrium system is disturbed by the removal of the reactant; the system will remedy this by trying to re-establish the equilibrium to the left to generate more reactants.
63
How would decreasing the volume of the following systems affect their equilibrium?
Decreasing the volume of a system causes the equilibrium to shift towards the side whose sum of the stoichiometric coefficients of only the species in a gaseous state is smaller. If ∆n_gas is greater than 0, it shifts to the left. If ∆n_gas is less than 0, it shifts to the right.
a) CH_4 (g)+ 2 H_2 O (g) \rightleftharpoonsCO_2 (g)+ 4H_2 (g)
∆n_gas is 2, Since there are 3 moles of reactants and 5 moles of products, the reaction shifts to the left, towards the reactants.
b) CaCO_3 (s)\rightleftharpoonsCaO(s)+CO_2 (g)
∆n_gas is 1, since we only count the moles of gas, there is only one mole of gas in the products. Thus, the reaction shifts towards the reactants.
c) C(s)+O_2 (g)\rightleftharpoonsCO_2 (g)
∆n_gas is 0, since we only count the number of moles of species in their gaseous state. Thus, there is no shift in equilibrium despite change in volume.
71
Explain why dissociation diatomic elements from molecules to elements, such as the reaction O_2 (g)\rightleftharpoons2O(g), will always increase with an increase in temperature.
First, lets think about this logically. Breaking bonds, especially strong bonds in diatomic elements, requires energy. When you add more energy to the system, there is a higher amount of energy, and more bonds being broken.
Second, lets consider the equilibrium of this reaction. If we add heat to the reactants, the equilibrium shifts to the right, towards the products.
O_2 (g)+heat\rightleftharpoons2O(g)
→→ reaction shifts to products
1
Write a balanced equation & Kc expression for each reaction.
a) CH4 undergoes combustion to become gaseous carbon dioxide and liquid water
CH4 + 2O2 CO2 + 2H2O ; Kc = [CO2]/ ([CH4][O2]2)
b) Cl2O5 (g) decomposes into Cl2 and O2
2Cl2O5 (g) 2Cl2 + 5O2 ; Kc = {[Cl2]2[O2]5}/[N2O5]2
c) N2O5 decomposes into O2 and NO2
2N2O5O2 + 4NO2 ; Kc = {[NO2]4[O2]}/[N2O5]2
2
Based on the descriptions, write a balanced equation and its Kp expression for each reaction
a) SO2 (g) is converted to sulphur trioxide
2SO2(g)+ O2(g) 2SO3(g) ; Kp = (SO3)2/[(SO2)2(O2)]
b) N2 and H2 are converted to NH3
N2(g) + 3H2(g) 2NH3(g) ; Kp = (NH3)2/[N2)(H2)3
c) Solid carbon is heated with steam to produce hydrogen gas and carbon monoxide
C(s) + H2O(g) H2(g) + CO(g) ; Kp = [(H2)(CO)]/(H2O)
3
Write the Kc expression for:
a) CaCO3(s) CaO(s) + CO2(g)
Kc = [CO2]
b) N2 + O2 2NO
Kc = [NO]2/ {[N2][O2]}
c) 2NOCl 2NO + Cl2
Kc = {[NO]2[Cl2]}/[NOCl]2
29
Can a mixture of 1.5 mol CH3, 3 mol O2, 2 mol CO2, and 0.5 mol H2O be maintained in a 5 L flask (Kc = 175)? Explain.
-No. Q < K, so the reaction will shift to the right.
30
Is the following reaction in an 8 L flask at 273 K at equilibrium? Explain.
BaCl2(aq) + Na2SO4(aq) BaSO4(s) + 2NaCl(aq)
-No. Q > K, so the reactants are favored.
31
If 0.68 mol CH3OH, 0.54 mol CO, and 0.94 H2 are all added to a 5 L container at 500 K (Kc = 150), is the mixture at equilibrium? If not, which way will it shift?
No. Q < K, so it will shift to the right.
33
A mixture of 0.28 mol H2, 0.28 mol CO2, 0.22 mol CO, and 0.22 mol H2O is brough to equilibrium at 562 K in a 3.5 L flask. What are the equilibrium amounts of each? (Kc = 9.84)
CO2(g) + H2(g) CO(g) + H2O(l)
H2: 0.05657 mol
CO2: 0.05657 mol
CO: 0.080 mol
H2O: n/a
35
Starting with 0.217 mol NO2(g) and 0.423 mol O2(g) in a 2 L flask at 500 K, how many moles of NO(g) will be present at equilibrium? (Kc = 1.4 x 10-3)
NO + O2 NO2
- Moles NO: 0.008
37
How many moles of each substance will there be at equilibrium if 1 mol each of CO2 and COF2 are added?
2COF2(g) CO2(g) + CF4(g) at 300 K in a 4 L flask (Kc = 3.4 x 10-3)
COF2: 0.215 mol
CO2: 0.215 mol
CF4: 0.305 mol
39.
CS2(g) + 4H2(g) CH4(g) + 2H2S(g) (Kc= 3.5)
a) Which way will the reaction shift?
-To the right
b) How many moles of each will be present at equilibrium?
- 0.45, 0.3, 0.15, respectively
41
If 1.5 mols of PCl5 dissociate in a 2 L flask, what is the total equilibrium pressure at 375 K? (Kc = 3.0)
PCl5(g) Cl2(g) + PCl3(aq)
- 69.2 atm
43
In the reaction below, what are the concentrations of Cr3+ and Cr2+?
Pb(s) + 2Cr3+(aq) Pb2+(aq) + 2Cr2+(aq)
a) Cr3+: 2
b) Cr2+: 2
45.
One sketch below represents an initial nonequilibrium mixture in the reversible reaction:
\[ SO_2\; (g)+Cl_2\;(g) \rightleftharpoons SO_2Cl_2\;(g) \]
with
\[K_c= 4.0\]
Which of the other three sketches best represents an equilibrium mixture? Explain.
Solution
\[ [SO_2Cl_2]=4.0*[Cl_2]*[SO_2] \]
represents the best due to it having numbers of SO2Cl2,SO4,Cl2 molecules that are consistent with Kc. (b) has 12 SO2Cl2 molecules per unit volume, 1 Cl2 molecules per unit volume, 3 SO2 molecules per unit volume. They are the requisite number of each type of molecules needed to generate the excepted Kc.
53. Problem
1.11mol each of \(CO\) and \(Cl_2\) are introduced into an evacuated 2.97L flask, and the following equilibrium is established at 771 K.
\[ CO\;(g)+Cl_2\;(g) \rightleftharpoons COCl_2\; (g)\]
with
Kp=22.5
Calculate (a) the partial pressure of COCl2(g) (b) total gas pressure
Solution:
(a) P(CO)=P(Cl2)=nRT/V=1.11mol*0.08206Latmmol^-1K^-1*771K/2.97K=23.6atm
Equation: CO(g)+ Cl2(g)à COCl2 Kp=22.5
Initial: 23.6atm 23.6atm 0atm
Changes: -xatm -xatm +xatm
Equil: 23.6-xatm 23.6-xatm xatm
Kp=P(COCl2)/P(CO)P(Cl2)=22.5 x/(23.6-x)^2=x/(557.0-47.2x+x^2)
22.5(557.0-47.2x+x^2)=x=12532.5-1062x+22.5x^2=x
12532.5-1063x+22.5x^2=0
x=(-b+/-(b^2-4ac)^(1/2))/2a=(-(-1063)+/-((-1063)^2-4(22.5)(12532.5))^(1/2))/2(22.5)=69.04(too large),22.62
P(CO)=P(Cl2)=23.6atm-22.62atm=.98atm P(COCl2)=22.62 atm
(a) Ptotal=P(CO)+P(Cl2)+P(COCl2)=.98atm+.98atm+22.62atm=24.58atm
55. Problem
Explain how Le Chatelier’s pirinciple supports the fact that the continuous removal of one of the products of a chemical reaction has the effect of causing the reaction to go to completion.
Solution:
Makes Q less than K and reaction shift the right as result and change in pressure of a constant temp equilibrium mixture.
63. Problem
If the volume increases the system, what effect does it have on the equilibrium condition?
- \( C(s)+H_2O\;(g)\rightleftharpoons CO(g)+H_2\;(g) \)
- \( 4NH_3\;(g)+5O_2\;(g)\rightleftharpoons 4NO(g)+6\,H_2O(g) \)
- \( Ca(OH)_2\;(s)+CO_2\;(g) \rightleftharpoons CaCO_3(s)+H_2O(g) \)
Solution
- It shifts the right
- Shifts to the right
- No effect
71. Problem
Why the % molecules dissociate into atoms in reactions of I2(g)à2I(g) always raises with a. raise temp?
Solution:
Increasing temp adds heat and decreasing temp takes away the heat. When the temp raises, heat is absorbs increases and helps in breaking molecules into atoms. Lower temp, lower the % of dissociation and higher temp, higher % of dissociation.
73. Problem
Refer to Example 14-13. Suppose that 0.1L of the equilibrium mixture is diluted to 0.25L with water. What will be the new concentrations when equilibrium is re-established?
Solution:
Eq: Ag+(aq)+ Fe2+(aq)à Fe3+(aq)+ Ag(s) Kc=2.98
Initi: 0.31M 0.21M 0.19M
Ch: 0.12M 0.084M 0.076M
Equil: +xM +xM -xM
New: 0.12+x 0.0084+x 0.076-x
Kc=[Fe3+]/[Ag+][Fe2+]=2.98=0.076-x/(0.12+x)(0.084+x)
29.8(0.12+x)(0.084+x)=0.076-x
0.076-x=0.03+0.61x+2.98x^2 2.98x^2+1.16x-0.046=0
x=(-16.1+/-(2.59+0.55)^(1/2))/5.96=0.027,-0.57
[Fe2+]=0.084-0.57=-0.49M
[Fe2+]=0.084+0.027=0.111M [Ag+]=0.12+0.027=0.15M
[Fe3+]=0.076-0.027=0.049M
Kc=0.049M/(0.111M*0.15M)=2.94
75. Problem
Started with \(SO_3(g)\) at 1.00 atm, what will be the total pressure when equilibrium is reached in the following reaction at 700 K?
\[ 2\,SO_3\;(g) \rightleftharpoons 2\,SO_2\; (g)+O_2\;(g) \]
with
\[ K_p=1.65*10^{-5}\]
Solution:
Pressure: 2SO3(g)à 2SO2(g) + O2(g)
Initi: 1.00atm 0 0
Change: -2x +2x +x
Equil: 1.00-2x 2x x
Kp=(PSO2)^2(PO2)/(PSO3)^2
1.65*10^-5=(2x)^2(x)/(1.00-2x)^2
x=P02=0.0155atm
PSO2=2x=2(0.0155)=0.0310atm
PSO3=1.00-2x=[1.00-2(0.0155)]=[1.00-0.0310]=0.969atm
Ptot=PO2+PSO2+PSO3=(0.0115+0.0310+0.969) atm=1.016atm
77. Problem
Calculate the amount of SO2, O2, SO3 listed on (a) Figure 14-6(c); (b) Figure 14-7(b)
Solution:
(a)2SO3(g)à2SO2(g)+O2(g) Kc=1/2.8*10^2
I: 1.68mol 0.32 0.16
C: -2x +2x x
E: 1.68-2x 0.32+2x 0.16+x
3.57*10^-3=((((0.32+2x)^2)/10)*((0.16+x)/10)))/((1.68-2x)^2)/10
X=0.10755M
[SO3]=1.68-2(0.10755)=1.46mol
[SO2]=0.32+2(0.10755)=0.54mol
[O2]=0.16+0.10755=0.27mol
(b) 2SO2(g)+O2(g)à 2SO3(g) Kc=2.8*10^2
I: 0.32mol 0.16 0.68
C: -2x -x +2x
E: 0.32-2x 0.16-x 0.68+2x
Kc=[SO3]^2/[SO2]^2[O2]
2.8*10^2=((0.68+2x)^2)/(0.32-2x)^2(0.16-x)
X=0.0749M
[SO3]=0.68+2(0.0749)=0.83mol
[SO2]=0.32-2(0.0749)=0.17mol
[O2]=0.16-0.0749=0.085mol
79. Problem
Methanation reaction: methane is produced from a mixture of CO and H2.
CO(s)+3H2(g)àCH4(g)+H2O(g) change=-230kJ Kc=190 at 1000K
(a)Is the reaction favored at higher or lower temp? Higher or lower pressure? (b) 4mol of synthesis gas with a 3:1 ratio of H2(g) to CO(g) in a 15.0L flask. What is the mole fraction of CH4 at 1000k?
Solution:
(a) Reaction is exothermic. Lowering temp, shifts right and increase conversion of synthesis gas to methane. High pressure, shifts right and increase conversion of synthesis gas to methane
(b) CO(s) + 3H2(g)àCH4(g)+H2O(g)
I: 1mol/15L 3mol/15L 0 0
=0.0667M =0.2M
C: -x -3x +x +x
E: 0.0667-x 0.2-3x x x
Kc=[CH4][H20]/[CO][H2]^3
190=(x)((x)/(0.0667-x)(0.2-3x)^3
x=0.0424M
Mole fraction of CH4=equilibrium mol of CH4/total number of mol at
equilibrium
=0.0243mol/(0.0424+0.0424+0.0243+0.0728)=0.134mol
84. Problem:
Synthesis of ammounia at 500K, N2+(g)+3H2(g)à2NH3(g), Kp=8.71*10^-
2. N2 and H2 are mixed in a 1:7 ratio and total pressure is 1.00atm.Find the
mole % NH3 at equilibrium.
Solution:
Kp=(PNH3)^2/(PN2)(PH2)^3
= ((XNH3)^2/(XN2)(XH2)^3)*(1/(Ptotal)^2)
= ((XNH3)^2/1*(7)^2)*1/(1^2)
= 8.71*10^-2
(xNH3)^2/49=8.71*10^-2
(xNH3)^2=4.2679
xNH3=2.07
%Mol of NH3=mol/total mol*100%=2.07/1+7+2.07*(100%)=20.52%
102. Problem
Equilibrium is established in the reaction 2SO2(g)+O2(g)à2SO3(g) at a Temp where Kc=123. If the number of mol of SO3(g) in the equilibrium mixture is the same as the number of mol of SO2(g) (a) the number of mol of O2(g) is also equal to the number of mol of SO2(g) (b) the number of mol of O2(g) is half the number of mol of SO2 (c) [O2] may have any of several values (d) [O2]=0.008M
Solution
Kc=[SO3]^2/[SO2]^2[02]
= (x/V)^2/(x/V)^2[O2]
Kc=1/[O2]
123=1/[O2]
[O2]=0.008M
D is the correct answer
104. Problem
2NO2(g)à2NO(g)+O2(g), Kc=3.19*10^-12 at 184C. At 184C, the value of Kc for this reaction is (a) 0.9*10^6 (b) 7.5*10^2 (c) 5.6*10^5 (d) 2.8*10^5.
Solution
K’c=[NO2]/[NO][O2]^(1/2)
= 1/(Kc)^(1/2)
= 1/(3.19*10^-12)^(1/2)
=1/1.79*10^-6
= 5.6*10^5 (c) is correct
Q14.1
based on these descriptions, write a balanced equation for each reversible reaction.
- Oxygen gas oxidizes gaseous ammonia vapor to gaseous nitrogen and water vapor.
- Hydrogen gas reduces gaseous nitrogen dioxide to gaseous ammonia and water vapor.
- Liquid acetone is in equilibrium with its vapor.
S31
- 3 O2(g) + 4 NH3(g) ↔ 2 N2(g) + 6 H2O(g)
- 7 H2(g) + 2 NO2(g) ↔ 2 NH3(g) + 4 H2O(g)
- (CH3)2CO(l) ↔ (CH3)2CO(g)
Q13
For the following reactions, determine the equilibrium constant expression in terms of concentration.
- a) N2O4(g) ⇄ 2NO2(g)
- b)NH3(aq) + H2O(ℓ) ⇄ NH4+(aq) + OH-(aq)
- c)C(s) + H2O(g) ⇄ H2(g) + CO(g)
S13
a)Kc = [NO2]2/[N2O4]
b)KC=[NH4+][OH-]/[NH3]
c)KC=[H2][CO]/[H2O]
Q25
At a certain temperature 1L flask with .298mol PCl3(g) and 8.70*10^-3molPCl5(g). After the system reached equilibrium, 2*10^-3molCl2(g) was found in the flask.
Calculate equilibrium concentrations and the value of Kc and Kp assuming 298K.
PCl5 ⇄ PCl3 + Cl2
[i]8.7*10^-3mol .298 0
[c]-x +x +x=2*10^-3
[e]8.7*10^-3mol-x .298+x 2*10^-3
Kc=(.002)(.3)/.0067=.0896
Kp=Kc(RT)∆n
Kp=(.0821)(298)2-1
Kp=2.19
Q26
At 2000 K, Kc=0.154 for the reaction N2(g) + 3H2(g)⇄2NH3(g).
- Is the conversion of N2 (g) to 2NH3(g) favored at high or low pressures?
- If the equilibrium mixture is transferred from a 1.00 L flask to a 2.00L flask, will the number of moles of N2(g) increase, decrease, or remain unchanged?
- If H2 is added, which direction would the reaction shift?
S26
- High because the reactants have more moles than the products
- Increase
- Right
Q29
In the following reaction, which direction will the reaction favor if the initial concentration of O2and CO2 is 4 M, and Kc is 1.16 at 298 K?
4KO2(s) + 2CO2(g) ⇄ 2KCO3(s) + 3O2(g)
S29
Q= [O2]3 / [CO2]2
Q= 43 / 42= 4K<Q= reaction will shift left
Q49
At 338 K, pure PCl5 gas is present in a flask at a pressure of 26.7 kPa. At 473 K this is completely dissociated into PCl3 gas and Cl2 gas. Calculate the pressure in the flask at 473 K. No volume is specified, so take a convenient value, say V = 1.00 L. The equation for the reaction that occurs at 473 K is
S49
PCl5(g) ® PCl3(g) + Cl2(g)
At 338 K, moles of PCl5 gas = PV/(RT)
= (26.7 x 1.00)/(8.314 x 338) = 9.50 x 10-3 mol.
At 473 K, moles of gas present = 2 x 9.50 x 10-3 = 0.0190 mol.
Then, using the Ideal Gas Equation, the new pressure can be deduced.
P = nRT/V
= 0.0190 x 8.314 x 473/1.00 = 74.7 kPa
Q57
Predict the effects on the amount of \(NH_3\) in the following reaction
\[N_{2(g)}+3H_{2(g)} \rightleftharpoons 2NH_{3(g)}\]
with \(∆H=-46.11\)
when
- temperature is lowered
- introducing more H2
- doubling the vol. of the container.
S57
- amount will increase because this is an exothermic reaction
- amount will increase to obtain equilibrium
- amount will decrease to produce more moles of gas to fill the larger container
Q59
If the system is heated which direction will the equilibrium shift?
- 2CO2(g)⇔ 2CO(g)+O2(g) ∆Hº=566kj
- C2H4(g) + H2(g) ⇔ C2H6(g)
S59
- shifts to the right
- shifts to the left
Q61
If the volume of an equilibrium mixture of N2(g), H2 (g), and NH3 (g) is reduced by doubling the pressure, will PNH3 have increased, decreased, or remained the same when equilibrium is re established? Explain.
\[N_{2(g)}+3H_{2(g)} \rightleftharpoons 2NH_{3(g)}\]
Increase because the number of moles on the product side is less than the amount of moles on the reactant side, therefore, if there is an increase in pressure, the reaction will move toward the side with less moles.
Q63
If we increased the pressure for the following reactions, what would the effect on equilibrium be?
- 2A (g) + B (s) ⇄ 4C (g)
- 5A (g) + 2B(l) ⇄ C(s) + 4D(g)
- A(l) + 4B(g) + 2C (g) ⇄ 3D(s) + 5E(g)
S63
Pressure is the inverse of volume, so when we increase pressure, we are decreasing volume. A will result in a shift left, B will shift right, and C will shift left.

