Gas Equilibrium Constants
- Page ID
- 1370
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)\(K_c\) and \(K_p\) are the equilibrium constants of gaseous mixtures. However, the difference between the two constants is that \(K_c\) is defined by molar concentrations, whereas \(K_p\) is defined by the partial pressures of the gasses inside a closed system. The equilibrium constants do not include the concentrations of single components such as liquids and solid and they may have units depending on the nature of the reaction (although thermodynamic equilibrium constants do not).
Here are some easy steps on writing gas equilibrium constants (this is the same for finding Kc, Kp, Ksp, Q and etc.):.
- In equilibrium equations, even though the arrows point both ways (\( \rightleftharpoons \)) we usually associate the left as reactants and the right as products.
- The products are on the TOP of the fraction (the numerator).
- The reactants are on the BOTTOM of the fraction (the denominator).
- The concentrations of the products and reactants are always raised to the power of their coefficient in the balanced chemical equation.
- If any of the reactants or products are solids or liquids, their concentrations are equal to one because they are pure substances. (see Solubility Product Constant, Ksp)
The standard example of writing Gas Equilibrium Constants are:
\[ \ aA + bB \; \rightleftharpoons \; cC + dD \nonumber \]
\[ K_c = \dfrac{[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}} \nonumber \]
\[ K_p = \dfrac{(C)^{c}(D)^{d}} {(A)^{a}(B)^{b}} \nonumber \]
Consider the thermal decomposition of \( NH_4SH_{(s)} \):
\[ NH_4SH_{(s)} \rightleftharpoons NH_{3 (g)} + H_2S_{(g)} \nonumber \]
This also is related to Ksp
\[ K_c = \dfrac{[NH_{3}][H_{2}S]}{[NH_{4}SH]} \nonumber \]
but since \(NH_4SH\) is a solid, we get:
\[ K_c = \dfrac{[NH_{3}][H_{2}S]}{[1]} \nonumber \]
\[ K_c = [NH_{3}][H_{2}S] \nonumber \]
As for Kp, it is the same as Kc, but instead of brackets [ ], Kp uses parentheses ( ):
\[ K_p = \dfrac{(NH_{3})(H_{2}S)}{(NH_{4}SH)} \nonumber \]
\[ K_p = \dfrac{(NH_{3})(H_{2}S)}{(1)} \nonumber \]
\[ K_p = (NH_{3})(H_{2}S) \nonumber \]
Consider the double replacement reaction of hydrogen and iodine gas:
\[ H_2 (g) + I_2 (g) \rightleftharpoons 2HI (g) \nonumber \]
\[ K_c = \dfrac{[HI]^{2}}{[H_{2}][I_{2}]} \nonumber \]
\[ K_p = \dfrac{(HI)^{2}}{(H_{2})(I_{2})} \nonumber \]
Definition of \(K_c\) and \(K_p\)
\(K_c\) is an equilibrium constant in terms of molar concentrations and is usually defined as:
\[ K_c = \dfrac{[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}} \nonumber \]
in the general reaction,
\[ aA + bB \rightleftharpoons cC + dD\nonumber \]
If a large \(K_c\) is formed then there are more products formed. Inversely, a small \(K_c\) indicates that the reaction favors the reactants.
\(K_p\) is an equilibrium constant in terms of partial pressures. and is usually defined as:
\[ K_p = \dfrac{(C)^{c}(D)^{d}}{(A)^{a}(B)^{b}} \nonumber \]
for the general reaction
\[ aA + bB \rightleftharpoons cC + dD \nonumber \]
Homogeneous Equilibria: Reactants/Products all in a single phase. For example:
\[A_{(g)} + B_{(g)} \rightleftharpoons C_{(g)} + D_{(g)}\nonumber \]
Heterogeneous Equilibria: Reactants/Products in more than one phase. For example:
\[A_{(s)} + B_{(g)} \rightleftharpoons C_{(g)} + D_{(s)}\nonumber \]
The relationship between the two equilibrium constants are:
\[ K_p = K_c (RT)^{ \Delta{n}} \nonumber \]
or
\[K_c = \dfrac{K_p}{(RT)^{ \Delta{n}}}\nonumber \]
where,
- \( \Delta n \) = (Total moles of gas on the products side) - (Total moles of gas on the reactants side). Hence \( \Delta = (d + c) - (a + b)\nonumber \] [The lower case numbers are the exponents]
- \(R\) is the gas constant found in the ideal gas law (\(0.0821 \; \dfrac{Liter \; Atm}{Mole \; Kelvin}\))
Relating Gas Equilibrium Constants to Equilibrium (K)
The value of K depends on whether the solution being calculated for is using concentrations or partial pressures. The gas equilibrium constants relate to the equilibrium (K) because they are both derived from the ideal gas law (PV = nRT).
\(K_c\) is the concentration of the reaction, it is usually shown as:
\[ \dfrac{c[C]c[D]}{c[A]c[B]} \nonumber \]
\(K_p\) is the amount of partial pressure in the reaction, usually shown as:
\[ \dfrac{p(C)p(D)}{p(A)p(B)} \nonumber \]
As we have seen above, Kp = Kc (RT)\(\Delta{n}\),we can derive this formula from the Ideal Gas Law.
We know that Kc is in terms Molarity \(\left(\dfrac{Moles}{Liters}\right)\), and we can also arrange the Ideal Gas Law (PV = nRT) as: \(\left(\dfrac{n}{L}\right) = \left(\dfrac{P}{RT}\right)\).
We know that Partial Pressure is directly proportional to Concentration:
\(P = \left(\dfrac{n}{L}\right) * RT\) Pressure can be in units of: Pascal (Pa), Atmosphere (atm), or Torr.
Therefore we can replace Kc with Molarity: the equation become, Kp = Kc (RT)\(\Delta{n}\)
(RT)\(\Delta{n}\) = \(\dfrac{(RT)^{c}(RT)^{d}}{(RT)^{a}(RT)^{b}}\)
Also: \(\left(\dfrac{n}{L}\right) = \left(\dfrac{P}{RT}\right)\), can be shown as Kc = Kp (RT)
K is also written the same as Kc and Kp:
\(\ aA + bB \rightleftharpoons cC + dD\).
\( K = \dfrac{[C]^{c}[D]^{d}}{[A]^{a}[B]^{b}}\)
\[ 2 NOBr_{(g)} \rightleftharpoons 2 NO_{(s)} + Br_{2 (g)} \nonumber \]
Given:
- NOBr= 0.46 M
- NO= 0.1 M
- Br2 = 0.3M
To set up Kc, it is \(\dfrac{Products}{Reactants}\)
\[ Kc= \dfrac{[NO]^2 \; [Br_{2}]}{[NOBr]^2}\nonumber \]
\[ Kc =\dfrac{[0.1]^2 \; [0.3]}{[0.46]^2}\nonumber \]
Answer
Kc= 0.0142 M
N2O4 (l) is an important component of rocket fuel, At 25 °C N2O4 is a colorless gas that partially dissociates into NO2. The color of an equilibrium mixture of these 2 gasses depends on their relative proportions, which are dependent on temperature. Equilibrium is established in the reaction \( N_2O_4 (g) \rightleftharpoons 2NO_2 (g) \) at 25 °C.
Given:
- 3.00 L container
- 7.64 g N2O4
- 1.56 g NO2
What is the Kc for this reaction?
Solution
Step 1: Convert grams to moles
mol N2O4 = 7.64 g * \( \dfrac{1 mol N_2 O_4}{92.01 g} \) = 8.303 * 10-2 mol
mol NO2 = 1.56 g * \( \dfrac{1 mol NO_2}{46.01 g} \) = 3.391 * 10-2 mol
Step 2: Convert moles to Molarity (moles/L)
[N2O4] M = \(\dfrac{8.303 * 10^{-2} mol N_{2}O_{4}}{3.00 L}\) = 0.0277 M
[NO2] M = \(\dfrac{3.391 * 10^{-2} mol NO_{2}}{3.00 L}\) = 0.0113 M
Step 3: Write the Equilibrium constant for Kc:
\[K_{c} = \dfrac{[NO_{2}]^{2}}{[N_{2}O_{4}]} = \dfrac{[0.0113]^{2}}{[0.0277]} = 4.61 \times 10^{-3}\nonumber \]
Calculate Kp for the reaction
\[N_{2(g)} + O_{2(g)} \rightleftharpoons 2NO_{(g)}\nonumber \]
Given:
- N2= 0.79 moles
- O2 = 0.21 moles
- Temp = 2500 K
When equilibrium is established the mole percent of Nitrogen Oxide (NO) at 1.8%
1st step: Create an ICE table:
\[N_{2(g)} + O_{2(g)} \rightleftharpoons 2NO_{(g)}\nonumber \]
| ICE |
\(N_2\) |
\(O_2\) | \(NO\) |
|---|---|---|---|
| Initial | 0.79 mol | 0.21 mol | 0 mol |
| Change | -x | -x | +2x |
| Equilibrium | (0.79 - x) | (0.21 - x) | (2x + 0) |
2nd Step: Find the Mole Percent (%) of products
XNO= 0.018
Xtotal = (0.79-x)+(.021-x)+(2x)= 1
XNO = \(\dfrac{2x}{X_{total}}\)
0.018 = \(\dfrac{2x}{1}\)
x = 0.009
3rd Step: Set up an equation
Kp = \(\dfrac{p(NO)^{2}}{p(N_{2})p(O_{2})}\)
PV = NRT
\(P = \dfrac{\dfrac{[n(NO)(RT)]^{2}}{V^{2}}}{\dfrac{n(N_{2})(RT)}{V}\dfrac{n(O_{2})(RT)}{V}}\)
[Volume Cancels out]
\(P = \dfrac{n(NO)^{2}}{n(N_{2})n(O_{2})}\)
4th Step: Plug in values
\(K_{P} = \dfrac{(2x)^{2}}{(0.79-x)(0.21-x)}\)
x = 0.009
Kp = 2.1x10-3
How the Gas Equilibrium Constants Relate to Reaction Quotient (Q)
The process of finding the Reaction Quotient (Qc) is the same as finding Kc and Kp, where the products of the reaction is divided by the reactants of the reaction \(\left(\dfrac{Products}{Reactants}\right)\) at any time not necessarily at equilibrium.
If a problem asks you to find which way the reaction will shift in order to achieve equilibrium, and K is given, you would have to calculate for Q and compare the two numbers.
When comparing K and Q:
- K < Q : Since there are more products than reactants, the reaction will produce more reactants to reach equilibrium, the reaction favors the reactants.
- K > Q : Since there are more reactants than products, the reaction will produce more products to reach equilibrium, the reaction favors the products.
- K = Q : There is no change in the products nor reactants, so equilibrium is achieved.
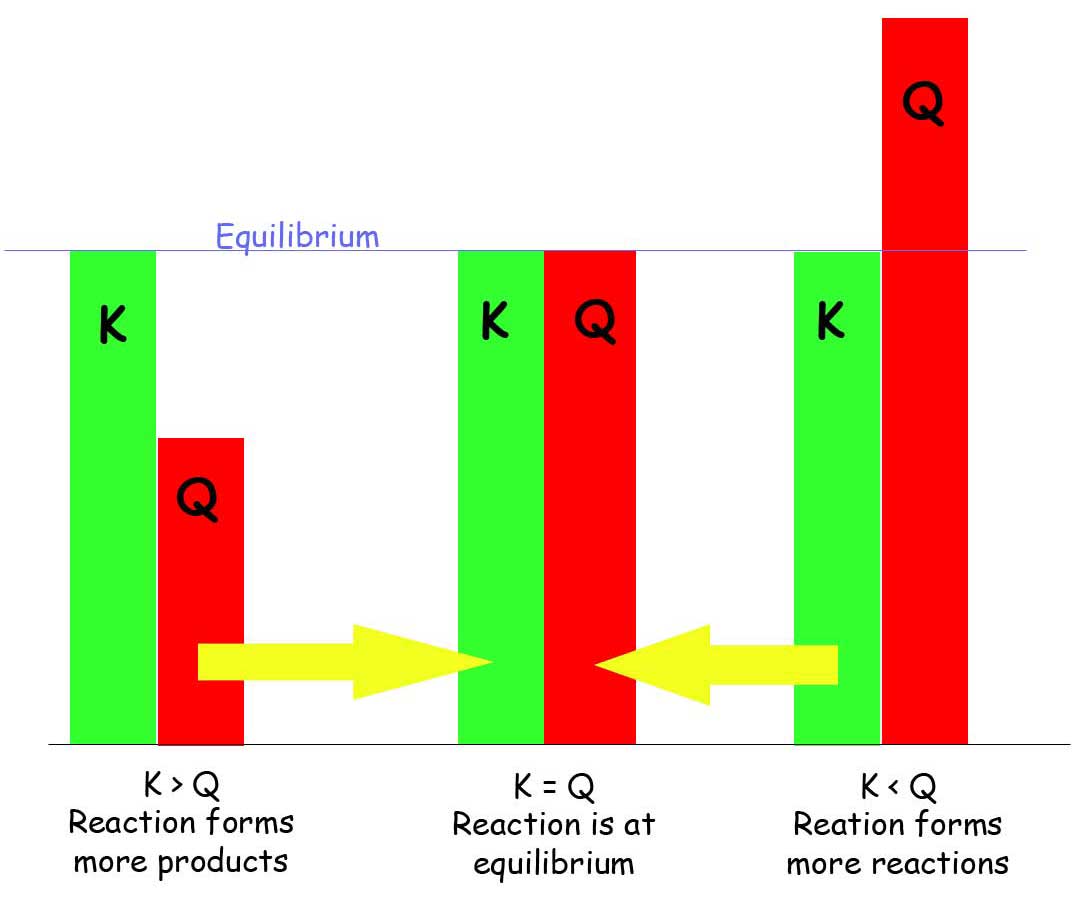
A trick to remember to which what the reaction will favor is:
Put:
K _ Q (in alphabetical order! - or it will not work)
K < Q : K \(\leftarrow\) Q
The reaction will favor the reactants because reactants are on the left of the equation.
K > Q : K \(\rightarrow\) Q
The reaction will favor the products because products are on the right of the equation.
K = Q : NO CHANGE
(See Relationship Between K and Q for more information)
\[ CO (g) + H_2O (g) \rightleftharpoons CO_2 (g) + H_2 (g) \nonumber \]
Given: Kc = 1.00 at about 1100 K
CO = 1.00 mol H2O = 1.00 mol CO2 = 2.00 mol H2 = 2.00 mol
Compared with their initial amounts, which of the substances will be present in a greater amount and which is in a lesser amount when equilibrium is established?
Solution
Step 1: Write out the expression for Qc
\[ Q_c = \dfrac{[CO_2][H_2]}{[CO][H_2O]} \nonumber \]
Step 2: Plug in the number of Molarity, since volume is not given, assume it is 1 Liters
\[ Q_c = \dfrac{[2.00][2.00]}{[1.00][1.00]} \nonumber \]
\[ Q_c = 4.00 \nonumber \]
Step 3: Compare Kc with Qc
Kc = 1.00 (unitless) Qc = 4.00 (unitless)
Kc < Qc
1.00 < 4.00
Therefore, the reaction will shift to the LEFT towards the reactants.
A mixture of hydrogen, iodine, and hydrogen iodide, each at 0.0020 M, was introduced into a container heated to 783 Kelvins. At this temperature \(K_c = 46\), Predict if more HI or less will be formed.
Solution
Step 1: Write out the reaction
\[ H_2 (g) + I_2 (g) \leftrightharpoons 2HI (g) \nonumber \]
Step 2: Write out the expression for Qc
\[ Q_c = \dfrac{[HI]^2}{[I_2][H_2]} \nonumber \]
Step 3: Plug in the Molarity given
Molarity = 0.0020 M
\[ Q_c = \dfrac{[0.0020]^{2}}{[0.0020][0.0020]} \nonumber \]
\[ Q_{c} = 1.00 \nonumber \]
Step 4: Compare Kc with Qc
Kc = 46 (unitless) Qc = 1.00 (unitless)
Kc > Qc
46 > 1.00
The reaction will shift to the RIGHT towards the products. Therefore, more HI will be produced.
References
- Petrucci, Ralph H., et al. General Chemistry: Principles and Modern Applications Ninth Edition. New Jersey: Pearson Prentice Hall, 2007. Print. (Pages 629-634 & problems/examples)
- Correia, Paiva, and Gil. "The Right Shift? A Problem in Chemical Equilibrium." Journal of Chemical Education: Journal 75.5 (2002) : 583. Web. May 1 2002. Link to this journal: pubs.acs.org/doi/abs/10.1021/ed079p583
- Rosenberg, Epstein, Krieger. College Chemistry 9th Edition. USA: The McGraw-Hill Companies, Inc. 2007
- Atkins, Peter and Jones, Loretta. Chemistry: Molecules, Matter, and Change Third Edition. USA: Second Printing, 1989. Print. (an image (modified it a little bit) and an example)
- Robinson, William R., Odom, Jerome D., and Holtzclaw, Henry F. Jr. Chemistry: Concepts and Models. Lexington, MA: D.C. Heath and Company, 1992. Print.
Problems
Below are practice problems for Kc and Kp:
Kc
1. Gaseous Hydrogen Iodide is placed in a closed container at 425 \(\circ\)C, Where it partially decomposes to Hydrogen and Iodine:
2HI (g) \(\rightleftharpoons\) H2 (g) + I2 (g)
The following are given:
[HI] = 3.53 * 10-3 M [H2] = 4.79 * 10-4 M [I2] = 4.79 * 10-4 M
What is the value of Kc at this temperature?
2. Write the Kc for the reaction and state where the reaction is Homogeneous or Heterogeneous.
a) N2 (g) + O2 (g) \(\rightleftharpoons\) 2NO (g)
b) FeO (s) + H2 (g) \(\rightleftharpoons\) Fe (s) + H2O (g)
3. Determine values of Kc from the Kp value given: (number 7 from p. 655 in the textbook)
2NO (g) + O2 (g) \(\rightleftharpoons\) 2NO2 (g); Kp = 1.48 * 104 at 184 \(\circ\)C
Kp
1. Write the Kp for the reaction and state where the reaction is Homogeneous or Heterogeneous.
a) 2C2H4 (g) + 2H2O (g) \(\rightleftharpoons\) 2C2H6 (g) + O2 (g)
b) Ti (s) + 2Cl2 (g) \(\rightleftharpoons\) TiCl4 (g)
2. Determine values of Kp from the Kc value given: (number 8 from p. 655 in the textbook)
2H2S (g) + CH4 (g) \(\rightleftharpoons\) 4H2 (g) + CS2 (g); Kc = 5.27 * 10-8 at 973 K.
3. The two common chlorides of Phosphorus, PCl3 and PCl5, both important in the production of other phosphorous compounds, coexist in equilibrium through: (number 17 from p. 655 in the textbook)
PCl3 (g) + Cl2 (g) \(\rightleftharpoons\) PCl5 (g)
At 250 \(\circ\)C, an equilibrium mixture in a 2.50 L flask contains 0.105 g PCl5, 0.220 g PCl3, and 2.12 g Cl2. What are the values of (a) Kc and (b) Kp for this reaction?
Answers
Kc
1. 2HI (g) \(\rightleftharpoons\) H2 (g) + I2 (g)
[HI] = 3.53 * 10-3 M [H2] = 4.79 * 10-4 M [I2] = 4.79 * 10-4 M
Kc = \(\dfrac{[H_{2}][I_{2}]}{[HI]^{2}}\)
Kc = \(\dfrac{[4.79 * 10^{-4} M][4.79 * 10^{-4} M]}{[3.53 * 10^{-3} M]^{2}}\)
Kc = \(\dfrac{[2.29441 * 10^{-7}] M^{2}}{[1.24609 * 10^{-5}] M^{2}}\)
Kc = 1.841 * 10-2
2. a) N2 (g) + O2 (g) \(\rightleftharpoons\) 2NO (g)
Kc = \(\dfrac{[NO]^{2}}{[N_{2}][O_{2}]}\)
The reaction is a homogeneous reaction because the reactants/products all have the same phase.
b) FeO (s) + H2 (g) \(\rightleftharpoons\) Fe (s) + H2O (g)
Kc = \(\dfrac{[H_{2}O]}{[H_{2}]}\), FeO and Fe are solids so they are no included in equilibrium constants.
The reaction is a heterogeneous reaction because the reactants/products have different phases.
3. Converting to Kc from Kp (number 7 from p. 655 in the textbook)
2NO (g) + O2 (g) \(\rightleftharpoons\) 2NO2 (g)
Kp = 1.48 * 104 at 184 \(\circ\)C
We know that Kp = Kc (RT)\(\Delta{n}\), we are given Kp but not Kc, you can rearrange the equation to: \(K_{c} = \dfrac{K_{p}}{(RT)^{-\Delta{n}}}\)
Which can also be written as: Kc = Kp (RT)-\(\Delta{n}\)
Now that we have your formula, we need to convert 184 \(\circ\)C to Kelvin, K = 184 + 273 = 457K
Kc = \(\dfrac{[NO_{2}]^{2}}{[NO]^{2}[O_{2}]}\)
-\(\Delta{n}\) = (total number of moles of products) - (total number of moles in reactants)
-\(\Delta{n}\) = (2) - (3) = -1
\(\Delta{n}\) = -(-1)
R = 0.08206 \(\dfrac{Liter \; Atm}{Mole \; Kelvin}\)
Now, plug in all the numbers we found: Kc = Kp (RT)-\(\Delta{n}\)
Kc = (1.48 * 104)[(0.08206)(457K)]-(-1)
Kc = 5.5 * 105
[it would be the same if you used this equation: Kc = Kp (RT)]
Kp
1. a) 2C2H4 (g) + 2H2O (g) \(\rightleftharpoons\) 2C2H6 (g) + O2 (g)
Kp = \(\dfrac{[C_{2}H_{6}]^{2}[O_{2}]}{[C_{2}H_{4}]^{2}[H_{2}O]^{2}}\)
The reaction is a homogeneous reaction because the reactants/products all have the same phase.
b) Ti (s) + 2Cl2 (g) \(\rightleftharpoons\) TiCl4 (g)
Kp = \(\dfrac{[TiCl_{4}]}{[Cl_{2}]^{2}}\), Ti is a solid so it is not included in equilibrium constants.
The reaction is a heterogeneous reaction because the reactants/products have different phases.
2. Find Kp, when Kc is given: (number 8 from p. 655 in the textbook)
2H2S (g) + CH4 (g) \(\rightleftharpoons\) 4H2 (g) + CS2 (g)
Kc = 5.27 * 10-8 at 973 K.
Kp = Kc (RT)\(\Delta{n}\), since Temperature is already converted to Kelvin and R = 0.08206 \(\dfrac{Liter \; Atm}{Mole \; Kelvin}\)
We need to find Delta n: Kp = \(\dfrac{[H_{2}]^{4}[CS_{2}]}{[H_{2}S]^{2}[CH_{4}O]}\)
\(\Delta{n}\) = (total number of moles of products) - (total number of moles in reactants)
\(\Delta{n}\) = (5) - (3) = 2
We can plug in our numbers: Kp = (5.27 * 10-8)[(0.08206)(973)]2
Kp = 3.6 * 10-4
3. The two common chlorides of Phosphorus, PCl3 and PCl5, both important in the production of other phosphorous compounds, coexist in equilibrium through: (number 17 from p. 655 in the textbook)
PCl3 (g) + Cl2 (g) \(\rightleftharpoons\) PCl5 (g)
At 250 \(\circ\)C, an equilibrium mixture in a 2.50 L flask contains 0.105 g PCl5, 0.220 g PCl3, and 2.12 g Cl2. What are the values of:
(a) Kc
[We need to convert grams to Molarity (mol/L), so we multiply grams with the molar mass and divide by Liters.]
PCl5 = \(\dfrac{0.105 g}{2.50 L}\) \(* \dfrac{1 mol}{137.3 g}\) (Molar Mass) = 2.0173 * 10-4 M
PCl3 = \(\dfrac{0.220 g}{2.50 L}\) \(* \dfrac{1 mol}{137.3 g}\) (Molar Mass) = 6.4093 * 10-4 M
Cl2 = \(\dfrac{2.12 g}{2.50 L}\) \(* \dfrac{1 mol}{70.9 g}\) (Molar Mass) = 0.0119605
\( K_{c} = \dfrac{[PCl_{5}]}{[Cl_{2}][PCl_{3}]}\)
\( K_{c} = \dfrac{[2.0173 * 10^{-4}]}{[0.0119605][6.4093 * 10^{-4}]}\)
Kc = 26.32
(b) Kp
Kp = Kc (RT)\(\Delta{n}\)
We need to find: \(\Delta{n}\) and K, R = 0.08206 \(\dfrac{L atm}{mol K}\)
K = 250 \(\circ\)C + 273 = 523 K
\(\Delta{n}\) = (1) - (2) = -1
Kp = (26.32) [(0.08206 )(523)](-1)
Kp = 0.6133
Contributors
- Rubi Medrano, Sharon Wei (UCD)

