Difference Between K And Q
- Page ID
- 1378
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Sometimes it is necessary to determine in which direction a reaction will progress based on initial activities or concentrations. In these situations, the relationship between the reaction quotient, \(Q_c\), and the equilibrium constant, \(K_c\), is essential in solving for the net change. With this relationship, the direction in which a reaction will shift to achieve chemical equilibrium, whether to the left or the right, can be easily calculated.
Introduction
\(K_c\) can be used calculate the final concentrations at equilibrium for a reaction using an ICE table and the natural progression of the reaction, from left to right or from right to left. However, what if you do not know which way the reaction will progress? A simple relationship between \(K_c\) and the reaction quotient, known as \(Q_c\), can help. The reaction quotient, \(Q\), expresses the relative ratio of products to reactants at a given instant. Using either the initial concentrations or initial activities of all the components of the reaction, the progression of an reaction can easily be determined.
Given the general chemical reaction
\[ aA +bB \rightleftharpoons gG +hH \]
\(Q\) may be expressed as the following equations:
\[ Q= \dfrac{a_{init}^ga_{init}^h}{a_{init}^a a_{init}^b} \]
or
\[ Q_{c}= \dfrac{[G]_{init}^g[H]_{init}^h}{[A]_{init}^a[B]_{init}^b} \]
Remember that the concentrations of liquids and solids do not change, so they are excluded from the expression. As shown above, the value of \(Q\) can be found by raising the products to the power of their coefficients, or stoichiometric factors, divided by the reactants raised to their coefficients. If the concentration of products in the numerator is much larger than that of reactants in the denominator, \(Q\) will be a large value. On the other hand, a small amount of products (small numerator) divided by a large value for the concentration of reactants (large denominator) would result in a small value for Q. The expressions for Q are very similar to those for \(K\):
\[ K= \dfrac{a_G^g a_{H}^h}{a_{A}^a a_{B}^b} \]
or
\[ K_c = \dfrac{[G]^g [H]^h}{[A]^a [B]^b} \]
To determine which direction a reaction will go towards, simply compare \(Q_c\), the initial concentration ratio, to \(K_c\), the equilibrium constant, and evaluate the results.
Q vs. K: What Does It Mean?
When you set \(Q\) against \(K\), there are five possible relationships:
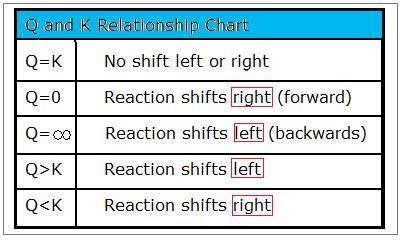
- \(Q=K\)
- \(Q=0\)
- \(Q<K\)
- \(Q= \infty\) and
- \(Q>K\).
To properly predict which way a reaction will progress, you must know these relationships.
Situation 1: Q = K
When Q=K, the system is at equilibrium and there is no shift to either the left or the right.
Take, for example, the reversible reaction shown below:
\[ CO_{(g)}+2H_{2 \; (g)} \rightleftharpoons CH_{3}OH_{(g)} \]
The value of Kc at 483 K is 14.5. If Q=14.5, the reaction is in equilibrium and will be no evolution of the reaction either forward or backwards.
Situation 2: Q < K
When Q<K, there are more reactants than products. As a result, some of the reactants will become products, causing the reaction to shift to the right.
Consider again:
\[ CO_{(g)}+2H_{2 \; (g)} \rightleftharpoons CH_{3}OH_{(g)} \]
For Q<K:
\[ CO_{(g)}+2H_{2 \; (g)} \longrightarrow CH_{3}OH_{(g)} \]
so that equilibrium may be established.
Q Equals Zero
If Q=0, then Q is less than K. Therefore, when Q=0, the reaction shifts to the right (forward). An easy way to remember this relationship is by thinking, “once you have nothing, the only thing left to do is to move forward.” If Q equals to zero, the reaction will shift forward (to the right):
\[ CO_{(g)}+2H_{2 \; (g)} \longrightarrow CH_{3}OH_{(g)} \]
Situation 3: Q > K
When Q>K, there are more products than reactants. To decrease the amount of products, the reaction will shift to the left and produce more reactants. For Q>K:
\[ CO_{(g)}+2H_{2 \; (g)} \longleftarrow CH_{3}OH_{(g)} \]
Q Equals Infinity
When Q=∞, the reaction shifts to the left (backwards). This is a variation of when Q>>>K.
\[ CO_{(g)}+2H_{2 \; (g)} \longleftarrow CH_{3}OH_{(g)} \]
Remembering the Relationship Between K and Q
An easy way to remember these relationships is by thinking of the > or < as the mouth of an alligator. The alligator will "eat" in the direction that the reaction shifts as long as \(Q\) is written before \(K\).

Handy Chart Outlining the Relationships of Q and K
Remembering these simple relationships will aid you to solving for the progression of a reaction. A chart outlining them can be found below.
Predicting the Shift of a Reaction Without Calculations
Depending on what a problem asks of you, sometimes it is unnecessary to make any calculations at all. Take, for example, the now familiar reversible reaction listed below:
\[ CO_{(g)}+2H_{2 \; (g)} \rightleftharpoons CH_{3}OH_{(g)} \]
What do you think will happen if more of the product, methanol (CH3OH), is added? Equilibrium will be disrupted, and the increase in products mean that Q>K. In order to re-establish equilibrium, the reaction will progress to the left, towards the reactants. This means some of the added methanol will break down into carbon monoxide and hydrogen gas.
\[ CO_{(g)}+2H_{2 \; (g)} \longleftarrow CH_{3}OH_{(g)} \]
Now, what if more of the reactants, carbon monoxide and hydrogen gas, are a? You should realize that this would upset the equilibrium. Q<K, because the value for the amount of reactants, or the denominator of the Q expression, has increased. To establish equilibrium again, the reaction will favor the product, so the reaction will progress to the right.
\[ CO_{(g)}+2H_{2 \; (g)} \longrightarrow CH_{3}OH_{(g)} \]
The ideas illustrated above show Le Chatelier's Principle whereby when an equilibrated system is subjected to a change in temperature, pressure, or concentration of a species in the reaction, the system responds by achieving a new equilibrium that partially offsets the impact of the change. Predicting which way a reaction will go can be the easiest thing that you will ever do in chemistry!
Example: Putting It All Together
To properly use the relationship between Q and K, you must know how to set it up. Take, for example, the reaction below:
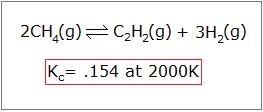
If you start with 4.00M CH4, 2.00M C2H2, and 3.00M H2, which direction will the reaction progress to reach equilibrium?

Problems
1) Consider this reaction:
\(2NOBr_{(g)} \leftrightharpoons 2NO_{(g)}+Br_{2}\)
If Kc= 0.0142 and the initial concentrations are 1.0 M NOBr, 0.2M NO, and 0.8M Br2, which way will the reaction progress to reach equilibrium?
2) What is Q and its purpose?
3) Consider the reaction following in equilibrium:
\(N_{2}O_{4 \; (g)} \leftrightharpoons 2NO_{2 \; (g)}\)
If more N2O4 is added, which way will the reaction proceed?
4) Consider the following reaction:
\(CO_{(g)}+Cl_{2 \; (g)} \leftrightharpoons COCl_{2 \; (g)}\)
With a Kc of 1.2 x 103 at 668 K, is the reaction in equilibrium when there are 5.00 mol CO(g), 2.00 mol Cl2(g), and 6.00 mol of COCl2(g) in a 3.00L flask? If not, which direction will the reaction progress to reach equilibrium?
5) Consider the following reaction:
\(H_{2 \; (g)}+I_{2 \; (g)} \leftrightharpoons 2HI_{(g)}\)
If Kc=50.2 at 718 K and the initial concentrations are 0.5 M H2, 0.15M I2, and 0.05M HI, which way will the reaction progress?
6) Consider the following reaction:
\(2COF_{2 \; (g)} \leftrightharpoons CO_{2 \; (g)}+CF_{4 \; (g)}\)
If Kc= 2.00 at 473 K and the initial concentrations are 2.0 M CO2, 4.0 M CF4, and 0.5 M COF2, which way will the reaction progress?
7) Consider the following reaction:
\(2SO_{2 \; (g)}+O_{2 \: (g)} \leftrightharpoons 2SO_{3 \; (g)}\)
Kc=100. With the initial masses of 20 g SO2, 13 g O2, and 25 g SO3 in a 5.0 L container, which way will the reaction progress.
Solutions
1) The reactions shifts to the left, towards the reactants.
NOBr= 1M, NO= 0.2M, Br2= 0.8M
\(Q_c= \dfrac {[0.2]^2 [0.8]}{[1]^2}\)
\(Q_c= 0.032\)
Therefore, Qc> Kc and the reactions shifts towards the reactants.
2) Q is a reaction quotient, which helps determine if a reaction will shift forward or backwards. As a system approaches towards equilibrium, Q approaches towards K.
3) The reaction will proceed to the right.
4) No, it is not at equilibrium. Since Q<K, the reaction will shift to the right to reach equilibrium.
5) Q = 0.033, so Q<K. The reaction will shift to the right.
6) Q = 32.0, so Q>K. The reaction will shift to the left.
7) Q = 12, so Q<K. The reaction will shift to the right.
References
- Alberty, R., A. Cornish-Bowden, et al. (1994). "Recommendations for nomenclature and tables in biochemical thermodynamics." Pure Appl. Chem 66: 1641–1666.
- Gold, J. and V. Gold (1985). "Le Chatelier's Principle and the Laws of van 't Hoff." Education in Chemistry 22: 82-85.
- Petrucci, Harwood, Herring, Madura. General Chemistry: Principles & MOdern Application. Ninth Edition. Pages 636-638.
Contributors and Attributions
- Rubi Medrano (UCD), Irene Ly (UCD)

