7.2: Intermolecular Interactions

Learning Objectives

• Name five kinds of molecular units that condensed matter can be composed of.
• Sketch out a potential energy curve, showing clearly the equilibrium separation and potential energy minimum.
• State the difference between bonded and non-bonded attractions.
• Explain the meaning and significance of the dipole moment of a molecule.
• Define induced dipole and polarizability.
• State the six kinds of intermolecular attractive forces and their relative strengths.

Liquids and solids differ from gases in that they are held together by forces that act between the individual molecular units of which they are composed. In this lesson we will take a closer look at these forces so that you can more easily understand, and in many cases predict, the diverse physical properties of the many kinds of solids and liquids we encounter in the world.

The very existence of condensed states of matter suggests that there are attractive forces acting between the basic molecular units of solids and liquids. The term molecular unit refers to the smallest discrete structural unit that makes up the liquid or solid. In most of the over 15 million chemical substances that are presently known, these structural units are actual molecules— that is, aggregates of atoms that have their own distinguishing properties, formulas, and molecular weights. But the molecular units can also be individual atoms, ions and more extended units. As with most artificial classifications, these distinctions tend to break down in extreme cases: most artificial polymers ("plastics") are composed of molecules of various sizes and shapes, some metal alloys contain identifiable molecular units, and it is not too much of a stretch to regard a diamond or a crystal of NaCl as a "molecule" in itself.

Potential Energy Curves

On the atomic or molecular scale, all particles exert both attractive and repulsive forces on each other. If the attractive forces between two or more atoms are strong enough to make them into an enduring unit with its own observable properties, we call the result a "molecule" and refer to the force as a "chemical bond".

Figure \(\PageIndex{1}\): Bonding vs. non-bonding interactions

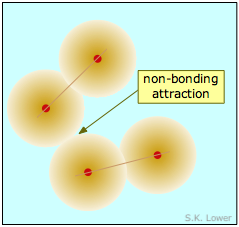
The two diatomic molecules depicted in Figure \(\PageIndex{1}\) have come into close contact with each other, but the attractive force that acts between them is not strong enough to bind them into a new molecular unit, so we call this force a non-bonding attraction. In the absence of these non-bonding attractions, all matter would exist in the gaseous state only; there would be no condensed phases.

Figure \(\PageIndex{2}\): Potential Energy curve for bonding and non-bonding interactions

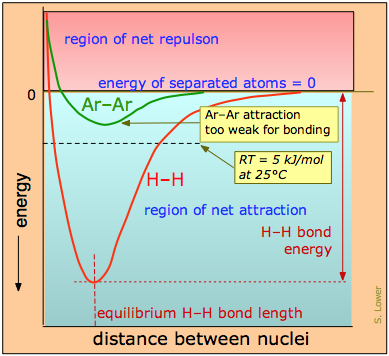
The distinction between bonding- and non-bonding attractions can be seen by comparing the potential energy plot for a pair of hydrogen atoms with that for two argon atoms (Figure \(\PageIndex{2}\)). As two hydrogen atoms are brought together, the potential energy falls to a minimum and then rises rapidly as the two electron clouds begin to repel each other. The potential energy minimum defines the energy and the average length of the H–H bond — two of its unique measurable properties.

The potential energy of a pair of argon atoms also falls as they are brought together, but not enough to hold them together. (e.g., the laws of quantum mechanics do not allow this noble gas element to form stable \(Ar_2\) molecules.) However, these non-bonding attractions enable argon to exist as a liquid and solid at low temperatures, but are unable to withstand disruptions caused by thermal energy at ordinary temperatures, so we commonly know argon as a gas.

Thermal Effects

From a classic pictures, at temperatures above absolute zero, all molecular-scale particles possess thermal energy that keeps them in constant motion (and from a quantum picture, motion does not stop even at absolute zero due to Heisenberg Uncertainly principle). The average thermal energy is given by the product of the gas constant R and the absolute temperature. At 25°C, this works out to

\[RT = (8.314 \,J \,K^{–1} mol^{–1}) (298\, K) = 2,480\, J\, mol^{–1} \approx 2.5\, kJ\, mol^{–1}\]

A functional chemical bond is much stronger than this (typically over 100 kJ/mol), so the effect of thermal motion is simply to cause the bond to vibrate; only at higher temperatures (where the value of RT is larger) will most bonds begin to break. Non-bonding attractive forces between pairs of atoms are generally too weak to sustain even a single vibration. In addition to unique distinguishing properties such as bond energy, bond length and stretching frequencies, covalent bonds usually have directional properties that depend on the orbital structures of the component atoms. The much-weaker non-bonding attractions possess none of these properties.

The shape of a potential energy curve (often approximated as a "Morse" curve) shows how repulsive and attractive forces affect the potential energy in opposite ways: repulsions always raise this energy, and attractions reduce it. The curve passes through a minimum when the attractive and repulsive forces are exactly in balance. As we stated above, all particles exert both kinds of forces on one another; these forces are all basically electrical in nature and they manifest themselves in various ways and with different strengths.

Figure \(\PageIndex{3}\): Intermolecular potential curves result from repulsion at short distances and attraction at longer distances

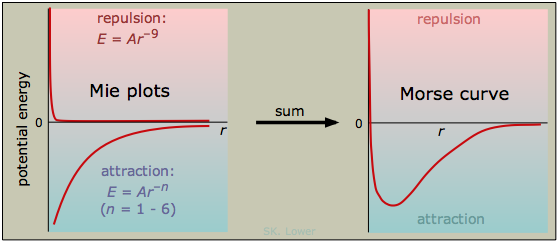
The distance corresponding to the minimum potential energy is known as the equilibrium distance. This is the average distance that will be maintained by the two particles if there are no other forces acting on them, such as might arise from the presence of other particles nearby. A general empirical expression for the interaction potential energy curve between two particles can be written as

\[ E = Ar^{-n} + Br^{-m} \label{7.2.1}\]

\(A\) and \(B\) are proportionality constants and \(n\) and \(m\) are integers. This expression is sometimes referred to as the Mie equation. The first term, \(A\), corresponds to repulsion is always positive, and \(n\) must be larger than \(m\), reflecting the fact that repulsion always dominates at small separations. The \(B\) coefficient is negative for attractive forces, but it will become positive for electrostatic repulsion between like charges. The larger the value of one of these exponents, the closer the particles must come before the force becomes significant. Table \(\PageIndex{1}\) lists the exponents for the types of interactions we will describe in this lesson.

Table \(\PageIndex{1}\): Classification of intermolecular forces

Species Involved	Type of Force	n	m
ions	Coulombic	-	1
ion - polar molecule	ion-dipole	-	2
two polar molecules	dipole-dipole	-	3
ion - nonpolar molecule	ion - induced dipole	-	4
polar and nonpolar molecule	dipole - induced dipole	-	6
nonpolar molecules	dispersion	-	6
repulsions	quantum	9	-
Note: the blue-shaded interactions are known collectively as van der Waals interactions

The Universal Repulsive Force

The value of \(n\) for the repulsive force in Figure \(\PageIndex{3}\) is 9; this may be the highest inverse-power law to be found in nature. The magnitude of such a force is negligible until the particles are almost in direct contact, but once it kicks in, it becomes very strong; if you want to get a feel for it, try banging your head into a concrete wall. Because the repulsive force is what prevents two atoms from occupying the same space, this is just what you would expect. If the repulsive force did not always win out against all attractive forces, all matter would collapse into one huge glob! The universal repulsive force arises directly from two main aspects of quantum theory.

1. First, the Heisenberg uncertainty principle tells us that the electrons situated within the confines of an atom possess kinetic energy that would exert an outward pressure were it not for the compensating attractive force of the positively-charged nucleus. But even the very slight decrease in volume that would result from squeezing the atom into a smaller space will raise this pressure so as to effectively resist this change in volume. This is the basic reason that condensed states of matter have extremely small compressibilities.
2. Working in concert with this is the Pauli exclusion principle each electron must have a different set of quantum numbers. So as two particles begin to intrude upon each other, the volume their electrons occupy gets divided up between each spin-pair, and the ones forced into higher quantum states would normally occupy even greater volumes. The effect is again to massively raise the potential energy as the particles begin to squeeze too close together.

In a wonderful article (Science 187 605-612 1975), the physicist Victor Weiskopf showed how these considerations, combined with a few fundamental constants, leads to realistic estimates of such things as the hardness and compressibility of solids, the heights of mountains, the lengths of ocean waves, and the sizes of stars.

Ion-Ion Interactions

Electrostatic attraction between electrically-charged particles is the strongest of all the intermolecular forces. These Coulombic forces (as they are often called) cause opposite charges to attract and like charges to repel.

Figure \(\PageIndex{1}\): Bonding vs. non-bonding interactions

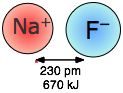
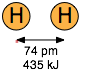
Coulombic forces are involved in all forms of chemical bonding; when they act between separate charged particles (ion-ion interactions) they are especially strong. Thus the energy required to pull a mole of Na⁺ and Cl^– ions apart in the sodium chloride crystal is greater than that needed to break the covalent bond in \(H_2\) (Figure \(\PageIndex{1}\)). The effects of ion-ion attraction are seen most directly in solids such as NaCl which consist of oppositely-charged ions arranged in two inter-penetrating crystal lattices.

According to Coulomb's Law the force between two charged particles is given by

\[ F= \dfrac{q_1q_2}{4\pi\epsilon_0 r^2} \label{7.2.2}\]

Instead of using SI units, chemists often prefer to express atomic-scale distances in picometers and charges as electron charge (±1, ±2, etc.) Using these units, the proportionality constant \(1/4\pi\epsilon\) works out to \(2.31 \times 10^{16}\; J\; pm\). The sign of \(F\) determines whether the force will be attractive (–) or repulsive (+); notice that the latter is the case whenever the two q's have the same sign.

Equation \(\ref{7.2.2}\) is an example of an inverse square law; the force falls off as the square of the distance. A similar law governs the manner in which the illumination falls off as you move away from a point light source; recall this the next time you walk away from a street light at night, and you will have some feeling for what an inverse square law means.

The stronger the attractive force acting between two particles, the greater the amount of work required to separate them. Work represents a flow of energy, so the foregoing statement is another way of saying that when two particles move in response to a force, their potential energy is lowered. This work, as you may recall if you have studied elementary mechanics, is found by integrating the negative force with respect to distance over the distance moved. Thus the energy that must be supplied in order to completely separate two oppositely-charged particles initially at a distance r₀ is given by

\[ w= - \int _{r_o} ^{\infty} \dfrac{q_1q_2}{4\pi\epsilon_0 r}dr =- \dfrac{q_1q_2}{4\pi\epsilon_0 r_o} \label{7.2.3}\]

Example \(\PageIndex{1}\)

When sodium chloride is melted, some of the ion pairs vaporize and form neutral NaCl molecules. How much energy would be released when one mole of Na⁺ and Cl^– ions are brought together in this way?

Solution

The energy released will be the same as the work required to separate

\[ \begin{align*} E &= \dfrac{(2.31 \times 10^{16} J pm) (+1) (–1)}{276\; pm} \\[4pt] &= –8.37 \times 10^{–19}\; J \end{align*} \]

The ion-ion interaction is the simplest of electrostatic interactions and other higher order interactions exists as discussed below.

Dipoles

According to Coulomb's law (Equation \(\ref{7.2.1}\)), the electrostatic force between an ion and an uncharged particle having Q = 0 should be zero. Bear in mind, however, that this formula assumes that the two particles are point charges having zero radii. A real particle such as an atom or a molecule occupies a certain volume of space. Even if the electric charges of the protons and electrons cancel out (as they will in any neutral atom or molecule), it is possible that the spatial distribution of the electron cloud representing the most loosely-bound [valence] electrons might be asymmetrical, giving rise to an electric dipole moment. There are two kinds of dipole moments:

• Permanent electric dipole moments can arise when bonding occurs between elements of differing electronegativities.
• Induced (temporary) dipole moments are created when an external electric field distorts the electron cloud of a neutral molecule.

An electric dipole refers to a separation of electric charge. An idealized electric dipole consists of two point charges of magnitude +q and –q separated by a distance r. Even though the overall system is electrically neutral, the charge separation gives rise to an electrostatic effect whose strength is expressed by the electric dipole moment given by

\[μ = q \times r \label{\(\PageIndex{5}\)}\]

Dipole moments possess both magnitude and direction, and are thus vectorial quantities; they are conventionally represented by arrows whose heads are at the negative end.

Permanent dipole moments

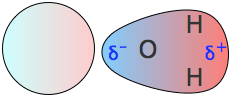
These are commonly referred to simply as "dipole moments". The most well-known molecule having a dipole moment is ordinary water. The charge imbalance arises because oxygen, with its nuclear charge of 8, pulls the electron cloud that comprises each O–H bond toward itself. These two "bond moments" add vectorially to produce the permanent dipole moment denoted by the red arrow. Note the use of the δ (Greek delta) symbol to denote the positive and negative ends of the dipoles.

Figure \(\PageIndex{5}\): Dipole Moment in water

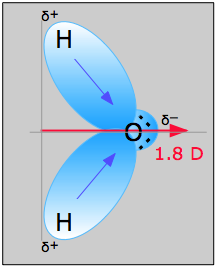
When an electric dipole is subjected to an external electric field, it will tend to orient itself so as to minimize the potential energy; that is, its negative end will tend to point toward the higher (more positive) electric potential. In liquids, thermal motions will act to disrupt this ordering, so the overall effect depends on the temperature. In condensed phases the local fields due to nearby ions or dipoles in a substance play an important role in determining the physical properties of the substance, and it is in this context that dipolar interactions are of interest to us here. We will discuss each kind of interaction in order of decreasing strength.

Induced dipoles

Even if a molecule is electrically neutral and possesses no permanent dipole moment, it can still be affected by an external electric field. Because all atoms and molecules are composed of charged particles (nuclei and electrons), the electric field of a nearby ion will cause the centers of positive and negative charges to shift in opposite directions. This effect, which is called polarization, results in the creation of a temporary, or induced dipole moment. The induced dipole then interacts with the species that produced it, resulting in a net attraction between the two particles.

The larger an atom or ion, the more loosely held are its outer electrons, and the more readily will the electron cloud by distorted by an external field. A quantity known as the polarizability expresses the magnitude of the temporary dipole that can be induced in it by a nearby charge.

Ion-Dipole interactions

A dipole that is close to a positive or negative ion will orient itself so that the end whose partial charge is opposite to the ion charge will point toward the ion. This kind of interaction is very important in aqueous solutions of ionic substances; H₂O is a highly polar molecule, so that in a solution of sodium chloride, for example, the Na⁺ ions will be enveloped by a shell of water molecules with their oxygen-ends pointing toward these ions, while H₂O molecules surrounding the Cl^– ions will have their hydrogen ends directed inward. As a consequence of ion-dipole interactions, all ionic species in aqueous solution are hydrated; this is what is denoted by the suffix in formulas such as K⁺(aq), etc.

Figure \(\PageIndex{6}\): Ion-Dipole Interaction between a sodium ion and water

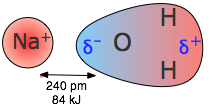
The strength of ion-dipole attraction depends on the magnitude of the dipole moment and on the charge density of the ion. This latter quantity is just the charge of the ion divided by its volume. Owing to their smaller sizes, positive ions tend to have larger charge densities than negative ions, and they should be more strongly hydrated in aqueous solution. The hydrogen ion, being nothing more than a bare proton of extremely small volume, has the highest charge density of any ion; it is for this reason that it exists entirely in its hydrated form H₃O⁺ in water.

Dipole-dipole interactions

As two dipoles approach each other, they will tend to orient themselves so that their oppositely-charged ends are adjacent. Two such arrangements are possible: the dipoles can be side by side but pointing in opposite directions, or they can be end to end. It can be shown that the end-to-end arrangement gives a lower potential energy.

Figure \(\PageIndex{7}\): Dipole-Dipole Interaction between a water molecule and a water molecule

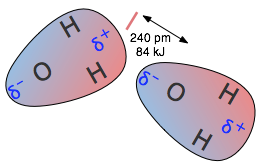
Dipole-dipole attraction is weaker than ion-dipole attraction, but it can still have significant effects if the dipole moments are large. The most important example of dipole-dipole attraction is hydrogen bonding.

Ion-induced dipole Interactions

The most significant induced dipole effects result from nearby ions, particularly cations (positive ions). Nearby ions can distort the electron clouds even in polar molecules, thus temporarily changing their dipole moments. The larger ions (especially negative ones such as SO₂^2– and ClO₄^2–) are highly polarizable, and the dipole moments induced in them by a cation can play a dominant role in compound formation.

Figure \(\PageIndex{8}\): Ion-Dipole Interaction between a sodium ion and water

Dipole-induced dipole interactions

A permanent dipole can induce a temporary one in a species that is normally nonpolar, and thus produce a net attractive force between the two particles (Figure \(\PageIndex{9}\)). This attraction is usually rather weak, but in a few cases it can lead to the formation of loosely-bound compounds. This effect explains the otherwise surprising observation that a wide variety of neutral molecules such as hydrocarbons, and even some of the noble gas elements, form stable hydrate compounds with water.

Figure \(\PageIndex{9}\): Dipole-induced dipole Interaction between a dipole and water

Dispersion (London) Forces

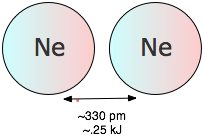
The fact that noble gas elements and completely non-polar molecules such as H₂ and N₂ can be condensed to liquids or solids tells us that there must be yet another source of attraction between particles that does not depend on the existence of permanent dipole moments in either particle (Figure \(\PageIndex{10}\)). To understand the origin of this effect, it is necessary to realize that when we say a molecule is “nonpolar”, we really mean that the time-averaged dipole moment is zero. This is the same kind of averaging we do when we draw a picture of an orbital, which represents all the locations in space in which an electron can be found with a certain minimum probability. On a very short time scale, however, the electron must be increasingly localized; not even quantum mechanics allows it to be in more than one place at any given instant. As a consequence, there is no guarantee that the distribution of negative charge around the center of an atom will be perfectly symmetrical at every instant; every atom therefore has a weak, fluctuating dipole moment that is continually disappearing and reappearing in another direction.

Figure \(\PageIndex{10}\): Dispersion Interaction between a dipole and water

Dispersion or London forces can be considered to be "spontaneous dipole - induced dipole" interactions.

Although these extremely short-lived fluctuations quickly average out to zero, they can still induce new dipoles in a neighboring atom or molecule, which helps sustain the original dipole and gives rise to a weak attractive force known as the dispersion or London force. Although dispersion forces are the weakest of all the intermolecular attractions, they are universally present. Their strength depends to a large measure on the number of electrons in a molecule. This can clearly be seen by looking at the noble gas elements in Table \(\PageIndex{2}\), whose ability to condense to liquids and freeze to solids is entirely dependent on dispersion forces.

Table \(\PageIndex{2}\): Intermolecular interactions in the noble gases

element	He	Ne	Ar	Kr	Xe
atomic number	2	10	18	36	54
boiling point, K	27	87	120	165	211
critical temperature, K	5	44	151	209.5	290
heat of vaporization, kJ mol^–1	0.08	1.76	6.51	59	12.6

It is important to note that dispersion forces are additive; if two elongated molecules find themselves side by side, dispersion force attractions will exist all along the regions where the two molecules are close. This can produce quite strong attractions between large polymeric molecules even in the absence of any stronger attractive forces.

"van der Waals" forces is a catch all Term

Although nonpolar molecules are by no means uncommon, many kinds of molecules possess permanent dipole moments, so liquids and solids composed of these species will be held together by a combination of dipole-dipole, dipole-induced dipole, and dispersion forces. These weaker forces (that is, those other than Coulombic attractions) are known collectively as van der Waals forces. These include attraction and repulsions between atoms, molecules, and surfaces, as well as other intermolecular forces. The term includes:

• force between two permanent dipoles and higher order moments like quadrupole
• force between a permanent dipole and a corresponding induced dipole
• force between two instantaneously induced dipoles (dispersion forces)

Table \(\PageIndex{3}\) shows some estimates of the contributions of the various types of van der Waals forces that act between several different types of molecules. Note particularly how important dispersion forces are in all of these examples, and how this, in turn, depends on the polarizability.

Table \(\PageIndex{3}\): Intermolecular interactions in the noble gases

Dubstance	Boiling Point °C	Dipole Moment D	Polarizability	% Dipole-induced Dipole	% Dipole-Dipole	% Dispersion
Ar	–186	0	1.6	0	0	100
CO	–190	0.1	2.0	0	0	100
HCl	–84	1.0	2.6	4.2	14.4	81.4
HBr	–67	0.8	3.6	2.2	3.3	94.5
HI	–35	0.4	5.4	0.4	0.1	99.5
NH3	–33	1.5	2.6	5.4	44.6	50.0
H2O	100	1.8	1.5	4.0	77.0	19.0