Polarizability
- Page ID
- 1663
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The term polarizability refers to the tendency of molecules to generate induced electric dipole moments when subjected to an electric field. It originates from the fact that nuclei and electrons are generally not fixed in space and that when molecules are subject to an electric field, the negatively charged electrons and positively charged atomic nuclei are subject to opposite forces and undergo charge separation. Polarizability allows us to better understand the interactions between nonpolar atoms and molecules and other electrically charged species, such as ions or polar molecules with dipole moments.
Introduction
Neutral nonpolar species have arrangements of electrons in their electron clouds that exhibit inversion symmetry through the center of the species (the electron density \(\rho(x,y,z) = \rho(-x, -y, -z)\)). When in the presence of an electric field, their electron clouds can be distorted (Figure \(\PageIndex{1}\)). The ease of this distortion is the polarizability of the atom or molecule. The created distortion of the electron cloud causes the originally nonpolar molecule or atom to acquire a dipole moment. This induced dipole moment is related to the polarizability of the molecule or atom and the strength of the electric field by the following equation:
\[μ_{ind} = \alpha E \label{1}\]
where \(E\) denotes the strength of the electric field and \(\alpha\) is the polarizability of the atom or molecule with units of C m2V-1.
In general, polarizability correlates with the interaction between electrons and the nucleus. The amount of electrons in a molecule affects how tight the nuclear charge can control the overall charge distribution. Atoms with fewer electrons will have smaller, denser electron clouds, as there is a strong interaction between the few electrons in the atoms’ orbitals and the positively charged nucleus. There is also less shielding in atoms with fewer electrons contributing to the stronger interaction of the outer electrons and the nucleus. With the electrons held tightly in place in these smaller atoms, these atoms are typically not easily polarized by external electric fields. In contrast, large atoms with many electrons, such as negative ions with excess electrons, are easily polarized. These atoms typically have very diffuse electron clouds and large atomic radii that limit the interaction of their external electrons and the nucleus.
The relationship between polarizability and the factors of electron density, atomic radii, and molecular orientation is as follows:
- The greater the number of electrons, the less control the nuclear charge has on charge distribution, and thus the increased polarizability of the atom.
- The greater the distance of electrons from nuclear charge, the less control the nuclear charge has on the charge distribution, and thus the increased polarizability of the atom.
- Molecular orientation with respect to an electric field can affect polarizability (labeled Orientation-dependent), except for molecules that are: tetrahedral, octahedral or icosahedral (labeled Orientation-independent). This factor is more important for unsaturated molecules that contain areas of electron-dense regions, such as 2,4-hexadiene. Greatest polarizability in these molecules is achieved when the electric field is applied parallel to the molecule rather than perpendicular to the molecule.
Polarizability Influences Dispersion Forces
The dispersion force is the weakest intermolecular force. It is an attractive force that arises from surrounding temporary dipole moments in nonpolar molecules or species. These temporary dipole moments arise when there are instantaneous deviations in the electron clouds of the nonpolar species. Surrounding molecules are influenced by these temporary dipole moments and a sort of chain reaction results in which subsequent weak, dipole-induced dipole interactions are created (Figure \(\PageIndex{2}\)).
These cumulative dipole-induced dipole interactions create attractive dispersion forces. Dispersion forces are the forces that make nonpolar substances condense to liquids and freeze into solids when the temperature is low enough.
Polarizability affects dispersion forces in the following ways:
- As polarizability increases, the dispersion forces also become stronger. Thus, molecules attract one another more strongly and melting and boiling points of covalent substances increase with larger molecular mass.
- Polarizability also affects dispersion forces through the molecular shape of the affected molecules. Elongated molecules with electrons that are delocalized (e.g., with double or triple bonds) will have some of those electrons easily shifted over a greater distance. This is manifested in an greater polarizability and thus greater dispersion forces.
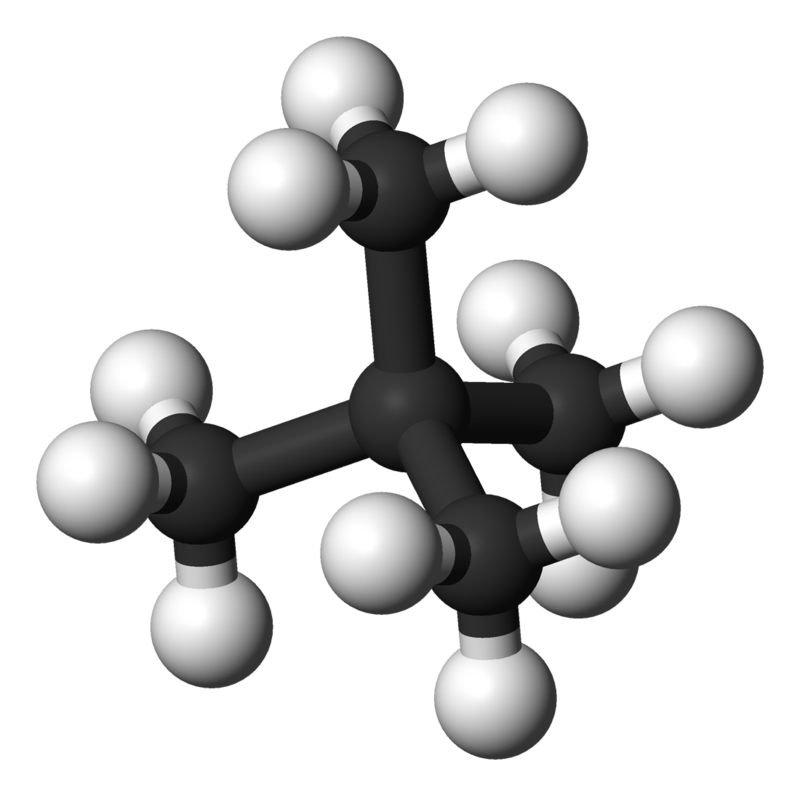
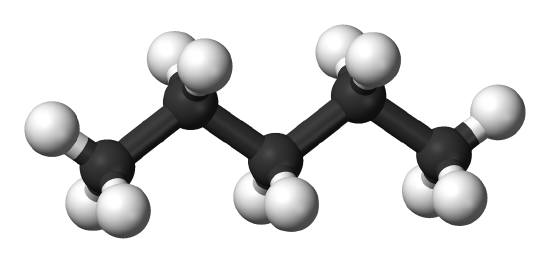
The influence of polarizability on the strength of the dispersion forces is also modulated by the 3-D structure of the molecules. For example, neo-pentane and n-pentane (Figure \(\PageIndex{3}\)) exhibit comparable polarizabilities, but have different boiling points. The lack of polar bonding in both indicates that dispersion is the dominant interaction responsible in both substances. The higher boiling point of n-pentane indicates there are stronger intermolecular interactions.
| molecule | Boiling Points (ºC) | \(\alpha\) (Å3) |
|---|---|---|
| neopentane | 9.5 | 10.24 |
| n-pentane | 36.0 | 9.879 |
Both neopentane and n-pentane would be expected to exhibits comparable dispersion forces since they have comparable polarizabilities. However, the structure of the n-pentane molecule facilitates greater dispersion forces due to more contacts between n-pentane molecules. In contrast, neopentane has a smaller dispersion force since the interactions between neopentane are reduced since neopentane is more compact and symmetrical.
The relationship between polarizability and dispersion forces can be seen in the following equation, which can be used to quantify the interaction between two like nonpolar atoms or molecules (e.g., \(\ce{A}\) with \(\ce{A}\)):
\[ V(r) = \dfrac{-3}{4} \dfrac{\alpha^2 I}{r^6} \label{2}\]
where \(r\) is the distance between the atoms or molecules, \(I\) is the first ionization energy of the atom or molecule, and \(\alpha\) is the polarizability constant expressed in units of m3.
This expression of \(\alpha\) is related to \(\alpha'\) by the following equation:
\[\alpha' = \dfrac{\alpha}{4 \pi \epsilon_o} \label{3}\]
To quantify the interaction between unlike atoms or molecules (\(\ce{A}\) and \(\ce{B}\)), Equation \(\ref{2}\) becomes:
\[ V(r) = \dfrac{-3}{2}\dfrac{I_AI_B}{I_A+I_B} \dfrac{\alpha_A \alpha_B}{r^6} \label{4}\]
References
- Petrucci, Ralph H., et al. General Chemistry: Principles and Modern Applications.Upper Saddle River, NJ: Prentice Hall, 2007
- Chang, Raymond. "Chapter 13: Intermolecular Forces/ Ion-Induced Dipole and Dipole-Induced Dipole Interactions/ Dispersion, or London, Interactions." Physical Chemistry for the Biosciences. Sansalito, CA: University Science, 2005. 495-98. Print.
- Housecroft, Catherine E., and Alan G. Sharpe. "Chapter 6: Structures and Energetics of Metallic and Ionic Solids." Inorganic Chemistry. Harlow [etc.: Prentice Hall, 2008. 173-74. Print.
- Miessler, Gary L., and Donald A. Tarr. "Chapter 6: Acid-Base and Donor-Acceptor Chemistry." Inorganic Chemistry. Upper Saddle River, NJ: Pearson Education, 2004. 183-86. Print

