Lennard-Jones Potential
- Page ID
- 1661
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Proposed by Sir John Edward Lennard-Jones, the Lennard-Jones potential describes the potential energy of interaction between two non-bonding atoms or molecules based on their distance of separation. The potential equation accounts for the difference between attractive forces (dipole-dipole, dipole-induced dipole, and London interactions) and repulsive forces.
Introduction
Imagine two rubber balls separated by a large distance. Both objects are far enough apart that they are not interacting. The two balls can be brought closer together with minimal energy, allowing interaction. The balls can continuously be brought closer together until they are touching. At this point, it becomes difficult to further decrease the distance between the two balls. To bring the balls any closer together, increasing amounts of energy must be added. This is because eventually, as the balls begin to invade each other’s space, they repel each other; the force of repulsion is far greater than the force of attraction.
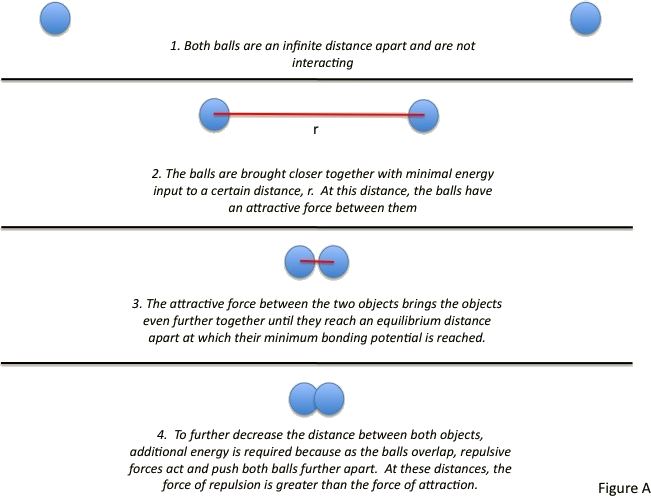
This scenario is similar to that which takes place in neutral atoms and molecules and is often described by the Lennard-Jones potential.
The Lennard-Jones Potential
The Lennard-Jones model consists of two 'parts'; a steep repulsive term, and smoother attractive term, representing the London dispersion forces. Apart from being an important model in itself, the Lennard-Jones potential frequently forms one of 'building blocks' of many force fields. It is worth mentioning that the 12-6 Lennard-Jones model is not the most faithful representation of the potential energy surface, but rather its use is widespread due to its computational expediency. The Lennard-Jones Potential is given by the following equation:
\[ V(r)= 4 \epsilon \left [ {\left (\dfrac{\sigma}{r} \right )}^{12}-{\left (\dfrac{\sigma}{r} \right )}^{6} \right] \label{1}\]
or is sometimes expressed as:
\[ V(r) = \frac{A}{r^{12}}- \dfrac{B}{r^6} \label{2}\]
where
- \(V\) is the intermolecular potential between the two atoms or molecules.
- \(\epsilon\) is the well depth and a measure of how strongly the two particles attract each other.
- \(\sigma\) is the distance at which the intermolecular potential between the two particles is zero (Figure \(\PageIndex{1}\)). \(\sigma\) gives a measurement of how close two nonbonding particles can get and is thus referred to as the van der Waals radius. It is equal to one-half of the internuclear distance between nonbonding particles.
- \(r\) is the distance of separation between both particles (measured from the center of one particle to the center of the other particle).
- \(A= 4\epsilon \sigma^{12}\), \(B= 4\epsilon \sigma^{6}\)
- Minimum value of \( \Phi_{12}(r) \) at \( r = r_{min} \).
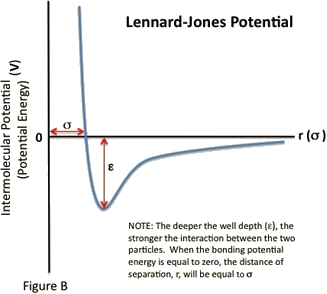
The \(\epsilon\) and \(\sigma\) values for Xenon (\(\ce{Xe}\)) are found to be 1.77 kJ/mol and 4.10 Angstroms, respectively. Determine the van der Waals radius for the Xenon atom.
Solution
Recall that the van der Waals radius is equal to one-half of the internuclear distance between nonbonding particles. Because \(\sigma\) gives a measure of how close two non-bonding particles can be, the van der Waals radius for Xenon (Xe) is given by:
r = \(\sigma\)/2 = 4.10 Angstroms/2 = 2.05 Angstroms
Bonding Potential
The Lennard-Jones potential is a function of the distance between the centers of two particles. When two non-bonding particles are an infinite distance apart, the possibility of them coming together and interacting is minimal. For simplicity's sake, their bonding potential energy is considered zero. However, as the distance of separation decreases, the probability of interaction increases. The particles come closer together until they reach a region of separation where the two particles become bound; their bonding potential energy decreases from zero to a negative quantity. While the particles are bound, the distance between their centers continue to decrease until the particles reach an equilibrium, specified by the separation distance at which the minimum potential energy is reached.
If the two bound particles are further pressed together, past their equilibrium distance, repulsion begins to occur: the particles are so close together that their electrons are forced to occupy each other’s orbitals. Repulsion occurs as each particle attempts to retain the space in their respective orbitals. Despite the repulsive force between both particles, their bonding potential energy increases rapidly as the distance of separation decreases.
Calculate the intermolecular potential between two Argon (Ar) atoms separated by a distance of 4.0 Angstroms (use \(\epsilon\)=0.997 kJ/mol and \(\sigma\)=3.40 Angstroms).
Solution
To solve for the intermolecular potential between the two Argon atoms, we use equation 2.1 where V is the intermolecular potential between two non-bonding particles.
\[ V= 4 \epsilon \left [ {\left (\dfrac{\sigma}{r} \right )}^{12}-{\left (\dfrac{\sigma}{r} \right )}^{6} \right] \nonumber\]
The data given are:
- \(\epsilon=0.997 ~\text{kJ/mol}\),
- \(\sigma=3.40 ~\text{Angstroms}\), and
- the distance of separation, \(r=4.0~\text{Angstroms}\).
We plug these values into Equation \ref{1} and solve as follows:
\[\begin{align*} V &= 4(0.997\;\text{kJ/mol}) \left[\left(\dfrac{3.40\;\text{Angstroms}}{4.0\;\text{Angstroms}}\right)^{12}-\left(\dfrac{3.40 \;\text{Angstroms}}{4.0 \;\text{Angstroms}}\right)^6\right] \\[4pt] &= 3.988(0.14-0.38) \\[4pt] & = 3.988(-0.24) \\[4pt] & = -0.96 kJ/mol \end{align*}\]
Stability and Force of Interactions
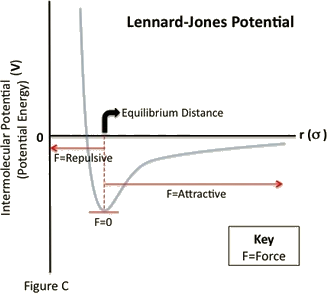
Like the bonding potential energy, the stability of an arrangement of atoms is a function of the Lennard-Jones separation distance. As the separation distance decreases below equilibrium, the potential energy becomes increasingly positive (indicating a repulsive force). Such a large potential energy is energetically unfavorable, as it indicates an overlapping of atomic orbitals. However, at long separation distances, the potential energy is negative and approaches zero as the separation distance increases to infinity (indicating an attractive force). This indicates that at long-range distances, the pair of atoms or molecules experiences a small stabilizing force. Lastly, as the separation between the two particles reaches a distance slightly greater than σ, the potential energy reaches a minimum value (indicating zero force). At this point, the pair of particles is most stable and will remain in that orientation until an external force is exerted upon it.
Two molecules, separated by a distance of 3.0 angstroms, are found to have a \(\sigma\) value of 4.10 angstroms. By decreasing the separation distance between both molecules to 2.0 angstroms, the intermolecular potential between the molecules becomes more negative. Do these molecules follow the Lennard-Jones potential? Why or why not?
Solution
Recall that \(\sigma\) is the distance at which the bonding potential between two particles is zero. On a graph of the Lennard-Jones potential, then, this value gives the x-intersection of the graph. According to the Lennard-Jones potential, any value of \(r\) greater than \(\sigma\) should yield a negative bonding potential and any value of r smaller than \(\sigma\) should yield a positive bonding potential. In this scenario, as the separation between the two molecules decreases from 3.0 angstroms to 2.0 angstroms, the bonding potential is becomes more negative. In essence however, because the starting separation (3.0 angstroms) is already less than \(\sigma\) (4.0 angstroms), decreasing the separation even further (2.0 angstroms) should result in a more positive bonding potential. Therefore, these molecules do not follow the Lennard-Jones potential.
The second part of the Lennard-Jones equation is (\(\sigma\)/r)6 and denotes attraction. Name at least three types of intermolecular interactions that represent attraction.
- Answer
-
From section 2.1, dipole-dipole, dipole-induced dipole, and London interactions are all attractive forces.
At what separation distance in the Lennard-Jones potential does a species have a repulsive force acting on it? An attractive force? No force?
- Answer
-
See Figure C. A species will have a repulsive force acting on it when r is less than the equilibrium distance between the particles. A species will have an attractive force acting on it when r is greater than the equilibrium distance between the particles. Lastly, when \(r\) is equal to t↑he equilibrium distance between both particles, the species will have no force acting upon it.
References
- Atkins, Peter and de Paula, Julio. Physical Chemistry for the Life Sciences. New York, N.Y. W. H. Freeman Company, 2006. (469-472).
- Royer, Donald J. Bonding Theory. New York, NY.:McGraw-Hill, Inc., 1968.
- Chang, Raymond. Physical Chemistry for the Biosciences. Sausalito, CA. University Science Books, 2005. (498-500)

