7.1: Matter under the Microscope

Learning Objectives

• State the major feature that characterizes a condensed state of matter.
• Describe some of the major observable properties that distinguish gases, liquid and solids, and state their relative magnitudes in these three states of matter.
• Describe the dominant forces and the resulting physical properties that distinguish ionic, covalent, metallic, and molecular solids.
• Explain the difference between crystalline and amorphous solids, and cite some examples of each.
• Name some of the basic molecular units from which solids of different type can be composed.
• What is meant by an "extended" or "infinite-molecule solid"?
• Describe some of the special properties of graphite and their structural basis.

Gases, liquids, and especially solids surround us and give form to our world. Chemistry at its most fundamental level is about atoms and the forces that act between them to form larger structural units. But the matter that we experience with our senses is far removed from this level. This unit will help you see how these macroscopic properties of matter depend on the microscopic particles of which it is composed.

Solids, Liquids and Gases

What distinguishes solids, liquids, and gases– the three major states of matter— from each other? Let us begin at the microscopic level, by reviewing what we know about gases, the simplest state in which matter can exist. At ordinary pressures, the molecules of a gas are so far apart that intermolecular forces have an insignificant effect on the random thermal motions of the individual particles. As the temperature decreases and the pressure increases, intermolecular attractions become more important, and there will be an increasing tendency for molecules to form temporary clusters. These are so short-lived, however, that even under extreme conditions, gases cannot be said to possess “structure” in the usual sense.

The contrast at the microscopic level between solids, liquids and gases is most clearly seen in the simplified schematic views above. The molecular units of crystalline solids tend to be highly ordered, with each unit occupying a fixed position with respect to the others. In liquids, the molecules are able to slip around each other, introducing an element of disorder and creating some void spaces that decrease the density. Gases present a picture of almost total disorder, with practically no restrictions on where any one molecule can be.

Having lived our lives in a world composed of solids, liquids, and gases, few of us ever have any difficulty deciding into which of these categories a given sample of matter falls. Our decision is most commonly based on purely visual cues:

• a gas has no definite boundaries other than those that might be imposed by the walls of a confining vessel.
• Liquids and solids possess a clearly delineated phase boundary that gives solids their definite shapes and whose light-reflecting properties enable us to distinguish one phase from another.
• Solids can have any conceivable shape, and their surfaces are usually too irregular to show specular (mirror-like) reflection of light. Liquids, on the other hand, are mobile; except when in the form of tiny droplets, liquids have no inherent shape of their own, but assume the shape of their container and show an approximately flat upper surface.

Our experience also tells us that these categories are quite distinct; a phase, which you will recall is a region of matter having uniform intensive properties, is either a gas, a liquid, or a solid. Thus the three states of matter are not simply three points on a continuum; when an ordinary solid melts, it usually does so at a definite temperature, without apparently passing through any states that are intermediate between a solid and a liquid.

Limiting Behavior

Although these common-sense perceptions are usually correct, they are not infallible, and in fact there are solids such as glasses and many plastics that do not have sharp melting points, but instead undergo a gradual transition from solid to liquid known as softening, and when subject to enough pressure, solids can exhibit something of the flow properties of liquids (glacial ice, for example).

Figure \(\PageIndex{1}\): Some solids can flow — slowly. Kluane Glacier in Canada's Yukon Territory. Typical glacial flow rates are 10-200 m/yr.

A more scientific approach would be to compare the macroscopic physical properties of the three states of matter, but even here we run into difficulty. It is true, for example, that the density of a gas is usually about a thousandth of that of the liquid or solid at the same temperature and pressure; thus one gram of water vapor at 100°C and 1 atm pressure occupies a volume of 1671 mL; when it condenses to liquid water at the same temperature, it occupies only 1.043 mL.

Table \(\PageIndex{1}\): Comparison of the molar volumes of neon in its three states.

Phase	Density
gas	22,400 cm^3/mol total volume (42 cm^3/mol excluded volume)
liquid	16.8 cm^3/mol
solid	13.9 cm^3/mol

Table \(\PageIndex{1}\) compares the molar volumes of neon in its three states. For the gaseous state, P = 1 atm and T = 0°C. The excluded volume is the volume actually taken up by the neon atoms according to the van der Waals equation of state model. It is this extreme contrast with the gaseous states that leads to the appellation “condensed states of matter” for liquids and solids. However, gases at very high pressures can have densities that exceed those of other solid and liquid substances, so density alone is not a sufficiently comprehensive criterion for distinguishing between the gaseous and condensed states of matter. Similarly, the density of a solid is usually greater than that of the corresponding liquid at the same temperature and pressure, but not always: you have certainly seen ice floating on water!

Example \(\PageIndex{1}\): Density of Xenon Gas

Compare the density of gaseous xenon (molar mass 131 g) at 100 atm and 0°C with that of a hydrocarbon liquid for which \(ρ = 0.104\, g/mL\) at the same temperature.

Solution

For simplicity, we will assume that xenon approximates an ideal gas under these conditions, which it really does not.

The ideal molar volume at 0° C and 1 atm is 22.4 L; at 100 atm, this would be reduced to 0.22 L or 220 mL, giving a density

\[ρ = \dfrac{131\, g}{224\, mL} = 0.58\, g/mL. \nonumber\]

In his autobiographical Uncle Tungsten, the physician/author Oliver Sacks describes his experience with xenon-filled balloons of "astonishing density — as near to 'lead balloons" as could be [imagined]. If one twirled these xenon balloons in one's hand, then stopped, the heavy gas, by its own momentum, would continue rotating for a minute, almost as if it were a liquid."

Other physical properties, such as the compressibility, surface tension, and viscosity, are somewhat more useful for distinguishing between the different states of matter. Even these, however, provide no well-defined dividing lines between the various states. Rather than try to develop a strict scheme for classifying the three states of matter, it will be more useful to simply present a few generalizations.

Table \(\PageIndex{2}\): Relative magnitudes of some properties of the three states of matter

property	gas	liquid	solid
density	very small	large	large
thermal expansion coefficient	large (= R/P)	small	small
cohesiveness	nil	small	large
surface tension	nil	medium	very large
viscosity	small	medium	very large
kinetic energy per molecule	large	small	smaller
disorder	random	medium	small

Condensed States of Matter

Some of these deal with macroscopic properties (that is, properties such as the density that relate to bulk matter), and others with microscopic properties that refer to the individual molecular units. Even the most casual inspection of the above table shows that solids and liquids possess an important commonality that distinguishes them from gases: in solids and liquids, the molecules are in contact with their neighbors. As a consequence, these condensed states of matter generally possess much higher densities than gases.

In our study of gases, we showed that the macroscopic properties of a gas (the pressure, volume, and temperature) are related through an equation of state, and that for the limiting case of an ideal gas, this equation of state can be derived from the relatively small set of assumptions of the kinetic molecular theory. To the extent that a volume of gas consists mostly of empty space, all gases have very similar properties. Equations of state work for gases because gases consist mostly of empty space, so intermolecular interactions can be largely neglected. In condensed matter, these interactions dominate, and they tend to be unique to each particular substance, so there is no such thing as a generally useful equation of state of liquids and solids.

Is there a somewhat more elaborate theory that can predict the behavior of the other two principal states of matter, liquids and solids? Very simply, the answer is "no"; despite much effort, no one has yet been able to derive a general equation of state for condensed states of matter. The best one can do is to construct models based on the imagined interplay of attractive and repulsive forces, and then test these models by computer simulation. Nevertheless, the very factors that would seem to make an equation of state for liquids and solids impossibly complicated also give rise to new effects that are easily observed, and which ultimately define the distinguishing characteristics of the gaseous, liquid, and solid states of matter. In this unit, we will try to learn something about these distinctions, and how they are affected by the chemical constitution of a substance.

Liquids

Crystalline solids and gases stand at the two extremes of the spectrum of perfect order and complete chaos. Liquids display elements of both qualities, and both in limited and imperfect ways. Liquids and solids share most of the properties of having their molecular units in direct contact as discussed in the previous section on condensed states of matter. At they same time, liquids, like gases, are fluids, meaning that their molecular units can move more or less independently of each other. But whereas the volume of a gas depends entirely on the pressure (and thus generally on the volume within which it is confined), the volume of a liquid is largely independent of the pressure. Here we offer just enough to help you see how they relate to the other major states of matter.

Solids

Of the four ancient elements of "fire, air, earth and water", it is the many forms of solids ("earths") that we encounter in daily life and which give form, color and variety to our visual world. The solid state, being the form of any substance that prevails at lower temperatures, is one in which thermal motion plays an even smaller role than in liquids. The thermal kinetic energy that the individual molecular units do have at temperatures below their melting points allows them to oscillate around a fixed center whose location is determined by the balance between local forces of attraction and repulsion due to neighboring units, but only very rarely will a molecule jump out of the fixed space allotted to it in the lattice. Thus solids, unlike liquids, exhibit long-range order, cohesiveness, and rigidity, and possess definite shapes.

Classification of solids

Most people who have lived in the world long enough to read this have already developed a rough way of categorizing solids on the basis of macroscopic properties they can easily observe; everyone knows that a piece of metal is fundamentally different from a rock or a chunk of wood. Unfortunately, nature's ingenuity is far too versatile to fit into any simple system of classifying solids, especially those composed of more than a single chemical substance.

Classification Scheme 1: According to bond type

The most commonly used classification is based on the kinds of forces that join the molecular units of a solid together. We can usually distinguish four major categories on the basis of properties such as general appearance, hardness, and melting point.

type of solid	molecular units	dominant forces	typical properties
ionic	ions	coulombic	high-melting, hard, brittle
covalent	atoms of electronegative elements	chemical bonds	non-melting (decompose), extremely hard
metallic	atoms of electropositive elements	mobile electrons	moderate-to-high melting, deformable, conductive, metallic luster
molecular	molecules	van der Waals	low-to-moderate mp, low hardness

It's important to understand that these four categories are in a sense idealizations that fail to reflect the diversity found in nature. The triangular diagram shown here illustrates this very nicely by displaying examples of binary compounds whose properties suggest that they fall somewhere other than at a vertex of the triangle.

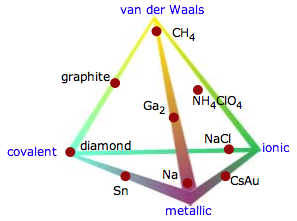
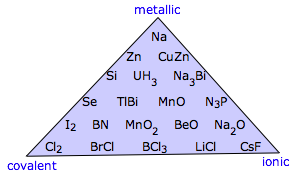
The triangle shown above excludes what is probably the largest category: molecular solids that are bound by van der Waals forces. One way of including these is to expand the triangle to a tetrahedron (the so-called Laing tetrahedron). Although this illustrates the concept, it is visually awkward to include many examples of the intermediate cases.

Classification Scheme 2: By type of Molecular Unit

Solids, like the other states of matter, can be classified according to whether their fundamental molecular units are atoms, electrically-neutral molecules, or ions. But solids possess an additional property that gases and liquids do not: an enduring structural arrangement of their molecular units. Over-simplifying only a bit, we can draw up a rough classification of solids according to the following scheme:

structure	atoms	molecules
array of discrete units	noble gas solids, metals	molecular solids
array of linked units	metals and covalent solids	"extended molecule" compounds
disordered arrangement	alternative forms of some elements (e.g. S, Se)	polymers, glasses

Classification Scheme 3: Classification by Dominant Attractive Force

Notice how the boiling points in the following selected examples reflect the major type of attractive force that binds the molecular units together. Bear in mind, however, that more than one type of attractive force can be operative in many substances.

substance	bp °C	molecular units	dominant attractive force	separation distance (pm)	attraction energy (kJ/mol)
sodium fluoride	990	Na^+ F^–	coulombic	18.8	657
sodium hydroxide	318	Na^+ OH^–	ion-dipole	21.4	90.4
water	100	H2O	dipole-dipole	23.7	20.2
neon	249	Ne	dispersion	33.0	0.26

Crystalline Solids

In a solid comprised of identical molecular units, the most favored (lowest potential energy) locations occur at regular intervals in space. If each of these locations is actually occupied, the solid is known as a perfect crystal. What really defines a crystalline solid is that its structure is composed of repeating unit cells each containing a small number of molecular units bearing a fixed geometric relation to one another. The resulting long-range order defines a three-dimensional geometric framework known as a lattice.

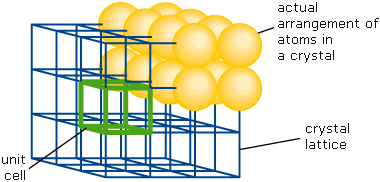
Geometric theory shows that only fourteen different types of lattices are possible in three dimensions, and that just six different unit cell arrangements can generate these lattices. The regularity of the external faces of crystals, which in fact correspond to lattice planes, reflects the long-range order inherent in the underlying structure. Perfection is no more attainable in a crystal than in anything else; real crystals contain defects of various kinds, such as lattice positions that are either vacant or occupied by impurities, or by abrupt displacements or dislocations of the lattice structure. Most pure substances, including the metallic elements, form crystalline solids. But there are some important exceptions.

Metallic Solids

In metals the valence electrons are free to wander throughout the solid, instead of being localized on one atom and shared with a neighboring one. The valence electrons behave very much like a mobile fluid in which the fixed lattice of atoms is immersed. This provides the ultimate in electron sharing, and creates a very strong binding effect in solids composed of elements that have the requisite number of electrons in their valence shells. The characteristic physical properties of metals such as their ability to bend and deform without breaking, their high thermal and electrical conductivities and their metallic sheen are all due to the fluid-like behavior of the valence electrons.

Molecular solids

Recall that a "molecule" is defined as a discrete aggregate of atoms bound together sufficiently tightly (that is, by directed covalent forces) to allow it to retain its individuality when the substance is dissolved, melted, or vaporized.

The two words italicized in the preceding sentence are important; covalent bonding implies that the forces acting between atoms within the molecule are much stronger than those acting between molecules, and the directional property of covalent bonding confers on each molecule a distinctive shape which affects a number of its properties. Most compounds of carbon — and therefore, most chemical substances, fall into this category.

Many simpler compounds also form molecules; H₂O, NH₃, CO₂, and PCl₅ are familiar examples. Some of the elements, such as H₂, O₂, O₃, P₄ and S₈ also occur as discrete molecules. Liquids and solids that are composed of molecules are held together by van der Waals forces, and many of their properties reflect this weak binding. Thus molecular solids tend to be soft or deformable, have low melting points, and are often sufficiently volatile to evaporate (sublime) directly into the gas phase; the latter property often gives such solids a distinctive odor.

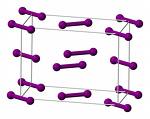
Iodine

Iodine is a good example of a volatile molecular crystal. The solid (mp 114° C , bp 184°) consists of I₂ molecules bound together only by dispersion forces. If you have ever worked with solid iodine in the laboratory, you will probably recall the smell and sight of its purple vapor which is easily seen in a closed container.

Because dispersion forces and the other van der Waals forces increase with the number of atoms, larger molecules are generally less volatile, and have higher melting points, than do the smaller ones. Also, as one moves down a column in the periodic table, the outer electrons are more loosely bound to the nucleus, increasing the polarizibility of the atom and thus its susceptibility to van der Waals-type interactions. This effect is particularly apparent in the progression of the boiling points of the successively heavier noble gas elements.

Covalent Solids

These are a class of extended-lattice compounds (see Section 6 below) in which each atom is covalently bonded to its nearest neighbors. This means that the entire crystal is in effect one super-giant “molecule”. The extraordinarily strong binding forces that join all adjacent atoms account for the extreme hardness of such substances; these solids cannot be broken or abraded without cleaving a large number of covalent chemical bonds. Similarly, a covalent solid cannot “melt” in the usual sense, since the entire crystal is its own giant molecule. When heated to very high temperatures, these solids usually decompose into their elements.

Diamond

Diamond is the hardest material known, defining the upper end of the 1-10 scale known as Mohs Hardness. Diamond cannot be melted; above 1700°C it is converted to graphite the more stable form of carbon.

Figure Rotating model of the diamond cubic crystal structure. Image used wtih pmerission (CC0; MarinaVladivostok via Wikicommons)

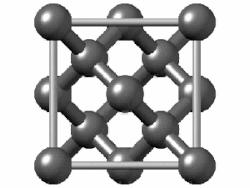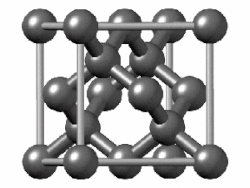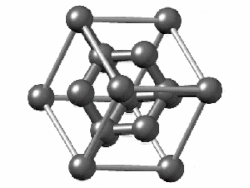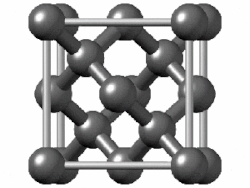
The diamond unit cell is face-centered cubic and contains 8 carbon atoms. The four darkly shaded ones are contained within the cell and are completely bonded to other members of the cell. The other carbon atoms (6 in faces and 4 at corners) have some bonds that extend to atoms in other cells. (Two of the carbons nearest the viewer are shown as open circles in order to more clearly reveal the bonding arrangement.)

Other covalent solids

Boron nitride BN is similar to carbon in that it exists as a diamond-like cubic polymorph as well as in a hexagonal form analogous to graphite. Cubic BN is the second hardest material after diamond, and finds use in industrial abrasives and cutting tools. Recent interest in BN has centered on its carbon-like ability to form nanotubes and related nanostructures.

Silicon carbide SiC is also known as carborundum. Its structure is very much like that of diamond with every other carbon replaced by silicon. On heating at atmospheric pressure, it decomposes at 2700°C, but has never been observed to melt. Structurally, it is very complex; at least 70 crystalline forms have been identified. Its extreme hardness and ease of synthesis have led to a diversity of applications — in cutting tools and abrasives, high-temperature semiconductors, and other high-temperature applications, manufacture of specialty steels, jewelry, and many more. Silicon carbide is an extremely rare mineral on the earth, and comes mostly from meteorites which are believed to have their origins in carbonaceous stars. The first synthetic SiC was made accidently by E.G. Acheson in 1891 who immediately recognized its industrial prospects and founded the Carborundum Co.

Tungsten carbide WC is probably the most widely-encountered covalent solid owing to its use in "carbide" cutting tools and as the material used to make the rotating balls in ball-point pens. It's high-melting (2870°C) form has a structure similar to that of diamond and is only slightly less hard. In many of its applications it is embedded in a softer matrix of cobalt or coated with titanium compounds.

Amorphous Solids

In some solids there is so little long-range order that the substance cannot be considered crystalline at all; such a solid is said to be amorphous. Amorphous solids possess short-range order but are devoid of any organized structure over longer distances; in this respect they resemble liquids. However, their rigidity and cohesiveness allow them to retain a definite shape, so for most practical purposes they can be considered to be solids.

Glasses refers generally to solids formed from their melts that do not return to their crystalline forms on cooling, but instead form hard, and often transparent amorphous solids. Although some organic substances such as sugar can form glasses ("rock candy"), the term more commonly describes inorganic compounds, especially those based on silica, SiO₂. Natural silica-based glasses, known as obsidian, are formed when certain volcanic magmas cool rapidly.

The difference between crystalline silica and silica glass is shown in these simplified two-dimensional projections. It is readily apparent that much of the ordered arrangement of crystalline silica is lost in the glassy form. But the glass retains enough Si–O bonds to form a hard, rigid material.

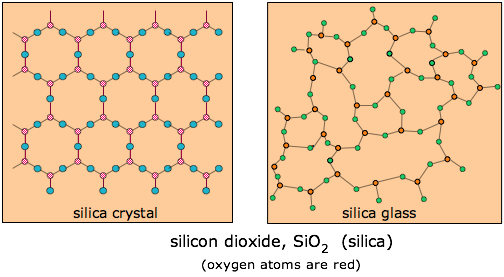
Ordinary glass is composed mostly of SiO₂, which usually exists in nature in a crystalline form known as quartz. If quartz (in the form of sand) is melted and allowed to cool, it becomes so viscous that the molecules are unable to move to the low potential energy positions they would occupy in the crystal lattice, so that the disorder present in the liquid gets “frozen into” the solid. In a sense, glass can be regarded as a supercooled liquid. Glasses are transparent because the distances over which disorder appears are small compared to the wavelength of visible light, so there is nothing to scatter the light and produce cloudiness.

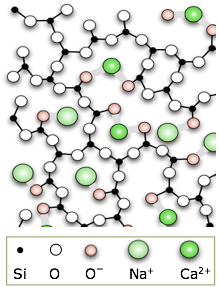
Ordinary glass is made by melting silica sand to which has been added some calcium and sodium carbonates. These additives reduce the melting point and make it more difficult for the SiO2 molecules to arrange themselves into crystalline order as the mixture cools. Glass is believed to have first been made in the Middle East at least as early as 3000 BCE. Its workability and ease of coloring has made it one of mankind's most important and versatile materials.

Types of molecular units

Molecules

Molecules, not surprisingly, are the most common building blocks of pure substances. Most of the 15-million-plus chemical substances presently known exist as distinct molecules. Chemists commonly divide molecular compounds into "small" and "large-molecule" types, the latter usually falling into the class of polymers (see below.) The dividing line between the two categories is not very well defined, and tends to be based more on the properties of the substance and how it is isolated and purified.

Atoms

We usually think of atoms as the building blocks of molecules, so the only pure substances that consist of plain atoms are those of some of the elements — mostly the metallic elements, and also the noble-gas elements. The latter do form liquids and crystalline solids, but only at very low temperatures. Although the metallic elements form crystalline solids that are essentially atomic in nature, the special properties that give rise to their "metallic" nature puts them into a category of their own. Most of the non-metallic elements exist under ordinary conditions as small molecules such as O₂ or S₆, or as extended structures that can have a somewhat polymeric nature. Many of these elements can form more than one kind of structure, each one stable under different ranges of temperature and pressure. Multiple structures of the same element are known as allotropes, although the more general term polymorph is now preferred.

Ions

Ions, you will recall, are atoms or molecules that have one or more electrons missing (positive ions) or in excess (negative ions), and therefore possess an electric charge. A basic law of nature, the electroneutrality principle, states that bulk matter cannot acquire more than a trifling (and chemically insignificant) net electric charge. So one important thing to know about ions is that in ordinary matter, whether in the solid, liquid, or gaseous state, any positive ions must be accompanied by a compensating number of negative ions. Ionic substances such as sodium chloride form crystalline solids that can be regarded as made of ions. These solids tend to be quite hard and have high melting points, reflecting the strong forces between oppositely-charged ions. Solid metal oxides, such as CaO and MgO which are composed of doubly-charged ions don't melt at all, but simply dissociate into the elements at very high temperatures.

Polymers

Plastics and natural materials such as rubber or cellulose are composed of very large molecules called polymers; many important biomolecules are also polymeric in nature. Owing to their great length, these molecules tend to become entangled in the liquid state, and are unable to separate to form a crystal lattice on cooling. In general, it is very difficult to get such substances to form anything other than amorphous solids.

Extended solids

actually exist in their solid forms as linked assemblies of these basic units arranged in chains or layers that extend indefinitely in one, two, or three dimensions. Thus the very simple models of chemical bonding that apply to the isolated molecules in gaseous form must be modified to account for bonding in some of these solids. The terms "one-dimensional" and "two-dimensional", commonly employed in this context, should more accurately be prefixed by "quasi-"; after all, even a single atom occupies three-dimensional space!

One-dimensional solids

Atoms of some elements such as sulfur and selenium can bond together in long chains of indefinite length, thus forming polymeric, amorphous solids. The most well known of these is the amorphous "plastic sulfur" formed when molten sulfur is cooled rapidly by pouring it into water.These are never the most common (or stable) forms of these elements, which prefer to form discrete molecules.

Rubber-like strands of plastic sulfur formed by pouring hot molten sulfur into cold water. After a few days, it will revert to ordinary crystalline sulfur. But small molecules can also form extended chains. Sulfur trioxide is a gas above room temperature, but when it freezes at 17°C the solid forms long chains in which each S atom is coordinated to four oxygen atoms.

Multi-dimensional solids

Many inorganic substances form crystalline solids which are built up from parallel chains in which the basic formula units are linked by weak bonds involving dipole-dipole and dipole-induced dipole interactions. Neighboring chains are bound mainly by dispersion forces.

Solid copper (II) chloride consists of multiple CuCl₂ units joined into long chains by covalent bonding. The chains are held together laterally by weaker van der Waals forces (mainly dispersion and ion-induced dipole). Each copper atom resides at the center of an imaginary octahedron whose vertices are defined by chlorine atoms in adjacent chains.

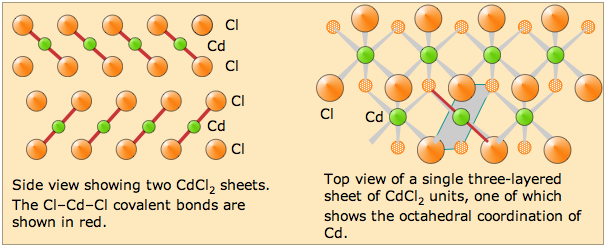
Layer or sheet-like structures

Solid cadmium chloride is a good example of a layer structure. The Cd and Cl atoms occupy separate layers; each of these layers extends out in a third dimension to form a sheet. The CdCl₂ crystal is built up from stacks of these layers held together by van der Waals forces.

Figure: \(\ce{CdCl2}\) lattice. Each Cd atom is covalently bonded to two chlorine atoms in adjacent layers; all other "bonds" are weak van der Waals attractions.

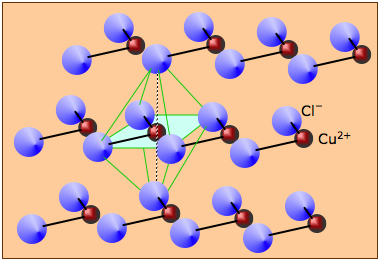
It's worth pointing out that although salts such as CuCl₂ and CdCl₂ are dissociated into ions when in aqueous solution, the solids themselves should not be regarded as "ionic solids". See also this section of the lesson on ionic solids.

Graphite

Graphite is a polymorph of carbon and its most stable form. It consists of sheets of fused benzene rings stacked in layers. The spacing between layers is sufficient to admit molecules of water vapor and other atmospheric gases which become absorbed in the interlamellar spaces and act as lubricants, allowing the layers to slip along each other. Thus graphite itself often has a flake-like character and is commonly used as a solid lubricant, although it loses this property in a vacuum.

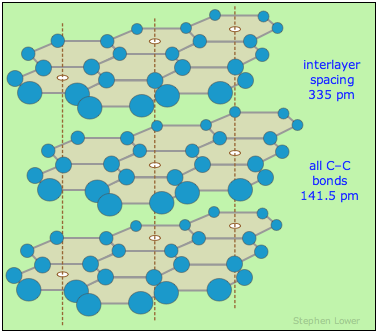
As would be expected from its anistropic structure, the electric and thermal conductivity of graphite are much greater in directions parallel to the layers than across the layers. The melting point of 4700-5000°C makes graphite useful as a high-temperature refractory material.

Graphite is the most common form of relatively pure carbon found in nature. Its name comes from the same root as the Greek word for "write" or "draw", reflecting its use as pencil "lead" since the 16th century. (The misnomer, which survives in common use, is due to its misidentification as an ore of the metallic element of the same name at a time long before modern chemistry had developed.)

Graphene

Graphene is a two-dimensional material consisting of a single layer of graphite — essentially "chicken wire made of carbon" that was discovered in 2004. Small fragments of graphene can be obtained by several methods; one is to attach a piece of Scotch Tape™ to a piece of graphite and then carefully pull it off (a process known as exfoliation.) Fragments of graphene are probably produced whenever one writes with a pencil.

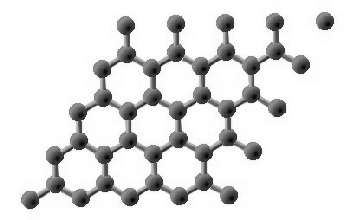
Graphene has properties that are uniquely different from all other solids. It is the strongest known material, and it exhibits extremely high electrical conductivity due to its massless electrons which are apparently able to travel at relativistic velocities through the layer.