6.6: Real Gases and Critical Phenomena
- Page ID
- 3565
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Make sure you thoroughly understand the following essential concepts that have been presented above.
- Real gases are subject to the effects of molecular volume (intermolecular repulsive force) and intermolecular attractive forces.
- The behavior of a real gas approximates that of an ideal gas as the pressure approaches zero.
- The effects of non-ideal behavior are best seen when the PV product is plotted as a function of P. You should be able to identify the regions of such a plot in which attractive and repulsive forces dominate.
- Each real gas has its own unique equation of state. Various general equations of state have been devised in which adjustable constants are used to approximate the behavior of a particular gas.
- The most well-known equation of state is that of van der Waals. Although you need not memorize this equation, you should be able to explain the significance of its terms.
The "ideal gas laws" as we know them do a remarkably good job of describing the behavior of a huge number chemically diverse substances as they exist in the gaseous state under ordinary environmental conditions, roughly around 1 atm pressure and a temperature of 300 K. But when the temperature is reduced, or the pressure is raised, the relation PV = constant that defines the ideal gas begins to break down, and its properties become unpredictable; eventually the gas condenses into a liquid. Why is this important? It is of obvious interest to a chemical engineer who needs to predict the properties of the gases involved in a chemical reaction carried out at several hundred atmospheres pressure. This is especially so when we consider that some of the basic tenets of the ideal gas model have to be abandoned in order to explain such properties as
- the average distance between collisions (the molecules really do take up space!)
- at sufficiently high pressures and low temperatures, intermolecular attractions assume control and the gas condenses to a liquid;
- the viscosity of a gas flowing through a pipe (the molecules do get temporarily "stuck" on the pipe surface, and are therefore affected by intermolecular attractive forces.)
Even so, many of the common laws such as Boyle's and Charles' continue to describe these gases quite well even under conditions where these phenomena are evident. Under ordinary environmental conditions (moderate pressures and above 0°C), the isotherms of substances we normally think of as gases don't appear to differ very greatly from the hyperbolic form
\[\dfrac{PV}{RT} = \text{constant} \label{6.6.1}\]
However, over a wider range of conditions, things begin to get more complicated. Thus isopentane (Figure \(\PageIndex{1}\)) behaves in a reasonably ideal manner above 210 K, but below this temperature the isotherms become somewhat distorted, and at 185 K and below they cease to be continuous, showing peculiar horizontal segments in which reducing the volume does not change the pressure.
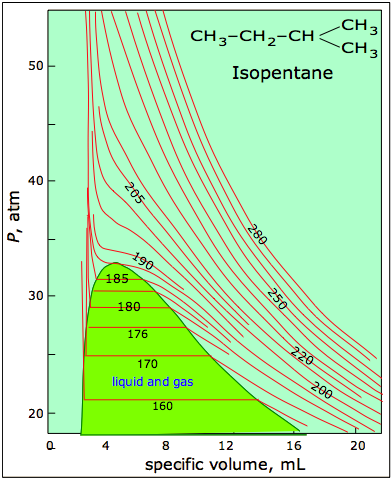
Within this region, any attempt to compress the gas simply "squeezes" some of it into the liquid state whose greater density exactly compensates for the smaller volume, thus maintaining the pressure at a constant value. It turns out that real gases eventually begin to follow their own unique equations of state, and ultimately even cease to be gases. In this unit we will see why this occurs, what the consequences are, and how we might modify the ideal gas equation of state to extend its usefulness over a greater range of temperatures and pressures.
Effects of Intermolecular Forces
According to Boyle's law, the product PV is a constant at any given temperature, so a plot of PV as a function of the pressure of an ideal gas yields a horizontal straight line. This implies that any increase in the pressure of the gas is exactly counteracted by a decrease in the volume as the molecules are crowded closer together. But we know that the molecules themselves are finite objects having volumes of their own, and this must place a lower limit on the volume into which they can be squeezed. So we must reformulate the ideal gas equation of state as a relation that is true only in the limiting case of zero pressure:
\[\lim_{P \rightarrow 0} PV=nRT \label{6.6.2}\]
So what happens when a real gas is subjected to a very high pressure? The outcome varies with both the molar mass of the gas and its temperature, but in general we can see the the effects of both repulsive and attractive intermolecular forces:
- Repulsive forces: As a gas is compressed, the individual molecules begin to get in each other's way, giving rise to a very strong repulsive force acts to oppose any further volume decrease. We would therefore expect the PV vs P line to curve upward at high pressures, and this is in fact what is observed for all gases at sufficiently high pressures.
- Attractive forces: At very close distances, all molecules repel each other as their electron clouds come into contact. At greater distances, however, brief statistical fluctuations in the distribution these electron clouds give rise to a universal attractive force between all molecules. The more electrons in the molecule (and thus the greater the molecular weight), the greater is this attractive force. As long as the energy of thermal motion dominates this attractive force, the substance remains in the gaseous state, but at sufficiently low temperatures the attractions dominate and the substance condenses to a liquid or solid.
The universal attractive force described above is known as the dispersion, or London force. There may also be additional (and usually stronger) attractive forces related to charge imbalance in the molecule or to hydrogen bonding. These various attractive forces are often referred to collectively as van der Waals forces. A plot of PV/RT as a function of pressure is a very sensitive indicator of deviations from ideal behavior, since such a plot is just a horizontal line for an ideal gas. Figures \(\PageIndex{2}\) and \(\PageIndex{3}\) demonstrate how these plots vary with the nature of the gas and with temperature, respectively.
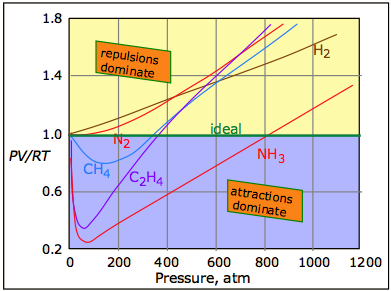
Intermolecular attractions, which generally increase with molecular weight, cause the PV product to decrease as higher pressures bring the molecules closer together and thus within the range of these attractive forces; the effect is to cause the volume to decrease more rapidly than it otherwise would. The repulsive forces always eventually win out. However, as the molecules begin to intrude on each others' territory, the stronger repulsive forces cause the curve to bend upward.
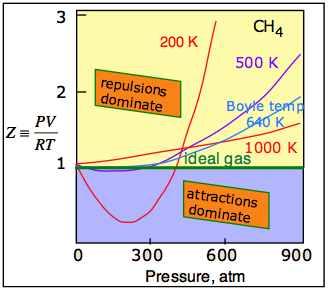
The temperature makes a big difference! At higher temperatures, increased thermal motions overcome the effects of intermolecular attractions which normally dominate at lower pressures (Figure \(\PageIndex{3}\)). So all gases behave more ideally at higher temperatures. For any gas, there is a special temperature (the Boyle temperature) at which attractive and repulsive forces exactly balance each other at zero pressure. As you can see in this plot for methane, some of this balance does remain as the pressure is increased.
The van der Waals Equation of State
How might we modify the ideal gas equation of state to take into account the effects of intermolecular interactions? The first and most well known answer to this question was offered by the Dutch scientist J.D. van der Waals (1837-1923) in 1873. The ideal gas model assumes that the gas molecules are merely points that occupy no volume; the "V" term in the equation is the volume of the container and is independent of the nature of the gas.

van der Waals recognized that the molecules themselves take up space that subtracts from the volume of the container (Figure \(\PageIndex{4}\)), so that the “volume of the gas” V in the ideal gas equation should be replaced by the term (\(V–b\)), in which \(b\) relates to the excluded volume, typically of the order of 20-100 cm3 mol–1. The excluded volume surrounding any molecule defines the closest possible approach of any two molecules during collision. Note that the excluded volume is greater then the volume of the molecule, its radius being half again as great as that of a spherical molecule.
The other effect that van der Waals needed to correct for are the intermolecular attractive forces. These are ignored in the ideal gas model, but in real gases they exert a small cohesive force between the molecules, thus helping to hold the gas together and reducing the pressure it exerts on the walls of the container.
Because this pressure depends on both the frequency and the intensity of collisions with the walls, the reduction in pressure is proportional to the square of the number of molecules per volume of space, and thus for a fixed number of molecules such as one mole, the reduction in pressure is inversely proportional to the square of the volume of the gas. The smaller the volume, the closer are the molecules and the greater will be the effect. The van der Walls equation replaces the \(P\) term in the ideal gas equation with \(P + (a / V^2)\) in which the magnitude of the constant a increases with the strength of the intermolecular attractive forces.
The complete van der Waals equation of state can be written as
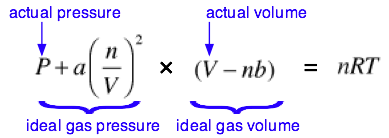
Although most students are not required to memorize this equation, you are expected to understand it and to explain the significance of the terms it contains. You should also understand that the van der Waals constants \(a\) and \(b\) must be determined empirically for every gas. This can be done by plotting the P-V behavior of the gas and adjusting the values of \(a\) and \(b\) until the van der Waals equation results in an identical plot. The constant a is related in a simple way to the molecular radius; thus the determination of \(a\) constitutes an indirect measurement of an important microscopic quantity.
|
Substance
|
molar mass (g) |
a (L2-atm mole–2)
|
b (L mol–1)
|
|---|---|---|---|
| hydrogen H2 | 2 | 0.244 | 0.0266 |
| helium He | 4 | 0.034 | 0.0237 |
| methane CH4 | 16 | 2.25 | 0.0428 |
| water H2O | 18 | 5.46 | 0.0305 |
| nitrogen N2 | 28 | 1.39 | 0.0391 |
| carbon dioxide CO2 | 44 | 3.59 | 0.0427 |
| carbon tetrachloride CCl4 | 154 | 20.4 | 0.1383 |
The van der Waals equation is only one of many equations of state for real gases. More elaborate equations are required to describe the behavior of gases over wider pressure ranges. These generally take account of higher-order nonlinear attractive forces, and require the use of more empirical constants. Although we will make no use of them in this course, they are widely employed in chemical engineering work in which the behavior of gases at high pressures must be accurately predicted.
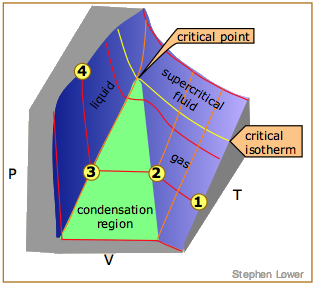
Condensation and the Critical Point
The most striking feature of real gases is that they cease to remain gases as the temperature is lowered and the pressure is increased. Figure \(\PageIndex{6}\) illustrates this behavior; as the volume is decreased, the lower-temperature isotherms suddenly change into straight lines. Under these conditions, the pressure remains constant as the volume is reduced. This can only mean that the gas is “disappearing" as we squeeze the system down to a smaller volume. In its place, we obtain a new state of matter, the liquid. In the green-shaded region, two phases, liquid, and gas, are simultaneously present. Finally, at very small volume all the gas has disappeared and only the liquid phase remains. At this point the isotherms bend strongly upward, reflecting our common experience that a liquid is practically incompressible.
To better understand this plot, look at the isotherm labeled  . As the gas is compressed from
. As the gas is compressed from  to
to  , the pressure rises in much the same way as Boyle's law predicts. Compression beyond
, the pressure rises in much the same way as Boyle's law predicts. Compression beyond  , however, does not cause any rise in the pressure. What happens instead is that some of the gas condenses to a liquid. At
, however, does not cause any rise in the pressure. What happens instead is that some of the gas condenses to a liquid. At  , the substance is entirely in its liquid state. The very steep rise to
, the substance is entirely in its liquid state. The very steep rise to corresponds to our ordinary experience that liquids have very low compressibilities. The range of volumes possible for the liquid diminishes as the critical temperature is approached.
corresponds to our ordinary experience that liquids have very low compressibilities. The range of volumes possible for the liquid diminishes as the critical temperature is approached.
The Critical Point
Liquid and gas can coexist only within the regions indicated by the green-shaded area in the diagram above. As the temperature and pressure rise, this region becomes more narrow, finally reaching zero width at the critical point. The values of P, T, and V at this juncture are known as the critical constants Pc , Tc , and Vc . The isotherm that passes through the critical point is called the critical isotherm. Beyond this isotherm, the gas and liquids become indistinguishable; there is only a single fluid phase, sometimes referred to as a supercritical liquid (Figure \(\PageIndex{7}\)).
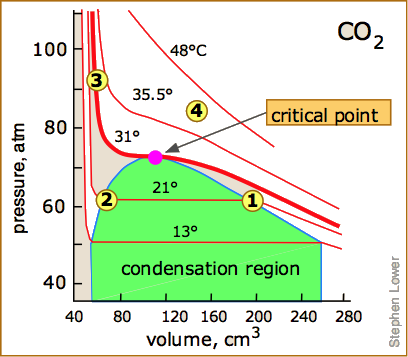
At temperatures below 31°C (the critical temperature), CO2 acts somewhat like an ideal gas even at a rather high pressure ( ). Below 31°, an attempt to compress the gas to a smaller volume eventually causes condensation to begin. Thus at 21°C, at a pressure of about 62 atm (
). Below 31°, an attempt to compress the gas to a smaller volume eventually causes condensation to begin. Thus at 21°C, at a pressure of about 62 atm ( ), the volume can be reduced from 200 cm3 to about 55 cm3 without any further rise in the pressure. Instead of the gas being compressed, it is replaced with the far more compact liquid as the gas is essentially being "squeezed" into its liquid phase. After all of the gas has disappeared (
), the volume can be reduced from 200 cm3 to about 55 cm3 without any further rise in the pressure. Instead of the gas being compressed, it is replaced with the far more compact liquid as the gas is essentially being "squeezed" into its liquid phase. After all of the gas has disappeared ( ), the pressure rises very rapidly because now all that remains is an almost incompressible liquid. Above this isotherm (
), the pressure rises very rapidly because now all that remains is an almost incompressible liquid. Above this isotherm ( ), CO2 exists only as a supercritical fluid.
), CO2 exists only as a supercritical fluid.
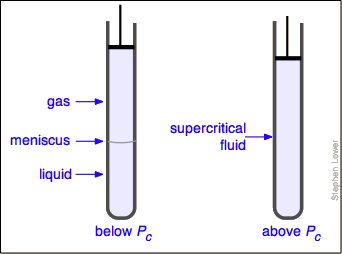
What happens if you have some liquid carbon dioxide in a transparent cylinder at just under its Pc of 62 atm, and you then compress it slightly? Nothing very dramatic until you notice that the meniscus has disappeared. By successively reducing and increasing the pressure, you can "turn the meniscus on and off".
One intriguing consequence of the very limited bounds of the liquid state is that you could start with a gas at large volume and low temperature, raise the temperature, reduce the volume, and then reduce the temperature so as to arrive at the liquid region at the lower left, without ever passing through the two-phase region, and thus without undergoing condensation!
Supercritical fluids
The supercritical state of matter, as the fluid above the critical point is often called, possesses the flow properties of a gas and the solvent properties of a liquid. The density of a supercritical fluid can be changed over a wide range by adjusting the pressure; this, in turn, changes its solubility, which can thus be optimized for a particular application. The picture at the right shows a commercial laboratory device used for carrying out chemical reactions under supercritical conditions.
Supercritical carbon dioxide is widely used to dissolve the caffeine out of coffee beans and as a dry-cleaning solvent. Supercritical water has recently attracted interest as a medium for chemically decomposing dangerous environmental pollutants such as PCBs. Supercritical fluids are being increasingly employed as as substitutes for organic solvents (so-called "green chemistry") in a range of industrial and laboratory processes. Applications that involve supercritical fluids include extractions, nano particle and nano structured film formation, supercritical drying, carbon capture and storage, as well as enhanced oil recovery studies.


