6.7: Solving Equilibrium Problems

Ladder diagrams are a useful tool for evaluating chemical reactivity and for providing a reasonable estimate of a chemical system’s composition at equilibrium. If we need a more exact quantitative description of the equilibrium condition, then a ladder diagram is insufficient; instead, we need to find an algebraic solution. In this section we will learn how to set‐up and solve equilibrium problems. We will start with a simple problem and work toward more complex problems.

A Simple Problem: The Solubility of Pb(IO₃)₂

If we place an insoluble compound such as Pb(IO₃)₂ in deionized water, the solid dissolves until the concentrations of Pb²⁺ and $\text{IO}_3^-$ satisfy the solubility product for Pb(IO₃)₂. At equilibrium the solution is saturated with Pb(IO₃)₂, which means simply that no more solid can dissolve. How do we determine the equilibrium concentrations of Pb²⁺ and $\text{IO}_3^-$, and what is the molar solubility of Pb(IO₃)₂ in this saturated solution?

When we first add solid Pb(IO₃)₂ to water, the concentrations of Pb²⁺ and $\text{IO}_3^-$ are zero and the reaction quotient, Q_r, is

$$Q_r = \left[\mathrm{Pb}^{2+}\right]\left[\mathrm{IO}_{3}^{-}\right]^{2}=0 \nonumber$$

As the solid dissolves, the concentrations of these ions increase, but Q_r remains smaller than K_sp. We reach equilibrium and “satisfy the solubility product” when Q_r = K_sp.

We begin by writing the equilibrium reaction and the solubility product expression for Pb(IO₃)₂.

$$\mathrm{Pb}\left(\mathrm{IO}_{3}\right)_{2}(s)\rightleftharpoons \mathrm{Pb}^{2+}(a q)+2 \mathrm{IO}_{3}^{-}(a q) \nonumber$$

e $$K_{\mathrm{sp}}=\left[\mathrm{Pb}^{2+}\right]\left[\mathrm{IO}_{3}^{-}\right]^{2}=2.5 \times 10^{-13} \label{6.1}$$

As Pb(IO₃)₂ dissolves, two $\text{IO}_3^-$ ions form for each ion of Pb²⁺. If we assume that the change in the molar concentration of Pb²⁺ at equilibrium is x, then the change in the molar concentration of $\text{IO}_3^-$ is 2x. The following table helps us keep track of the initial concentrations, the change in con‐ centrations, and the equilibrium concentrations of Pb2+ and $\text{IO}_3^-$.

concentrations	Pb(IO3)2 (s)	$\rightleftharpoons$	Pb^2^+ (aq)	+	2$\text{IO}_3^-$ (aq)
initial	solid		0		0
change	solid		+x		+ 2x
equilibrium	solid		x		2x

Because a solid, such as Pb(IO₃)₂ , does not appear in the solubility product expression, we do not need to keep track of its concentration. Remember, however, that the K_sp value applies only if there is some solid Pb(IO₃)₂ present at equilibrium.

Substituting the equilibrium concentrations into Equation $\ref{6.1}$ and solving gives

$$(x)(2 x)^{2}=4 x^{3}=2.5 \times 10^{-13} \nonumber$$

$$x=3.97 \times 10^{-5} \nonumber$$

Substituting this value of x back into the equilibrium concentration expressions for Pb²⁺ and $\text{IO}_3^-$ gives their concentrations as

$$\left[\mathrm{Pb}^{2+}\right]=x=4.0 \times 10^{-5} \mathrm{M} \text { and }\left[\mathrm{IO}_{3}^{-}\right]=2 x=7.9 \times 10^{-5} \nonumber$$

Because one mole of Pb(IO₃)₂ contains one mole of Pb²⁺, the molar solubility of Pb(IO₃)₂ is equal to the concentration of Pb²⁺, or $4.0 \times 10^{-5}$ M.

We can express a compound’s solubility in two ways: as its molar solubility (mol/L) or as its mass solubility (g/L). Be sure to express your answer clearly.

Exercise 6.7.1

Calculate the molar solubility and the mass solubility for Hg₂Cl₂, given the following solubility reaction and K_sp value.

$$\mathrm{Hg}_{2} \mathrm{Cl}_{2}(s)\rightleftharpoons \mathrm{Hg}_{2}^{2+}(a q)+2 \mathrm{Cl}^{-}(a q) \quad K_{\mathrm{sp}}=1.2 \times 10^{-8} \nonumber$$

Answer

When Hg₂Cl₂ dissolves, two Cl^– are produced for each ion of $\text{Hg}_2^{2+}$. If we assume x is the change in the molar concentration of $\text{Hg}_2^{2+}$, then the change in the molar concentration of Cl^– is 2x. The following table helps us keep track of our solution to this problem.

concentration	Hg2Cl2 (s)	$\rightleftharpoons$	$\text{Hg}_2^{2+}$ (aq)	+	Cl^–(aq)
initial	solid		0		0
change	solid		+x		+2x
equilibrium	solid		x		2x

Substituting the equilibrium concentrations into the K_sp expression forHg₂Cl₂ gives

$$K_{\mathrm{sp}}=\left[\mathrm{Hg}_{2}^{2+}\right]\left[\mathrm{Cl}^{-}\right]^{2}=(x)(2 \mathrm{x})^{2}=4 x^{3}=1.2 \times 10^{-18} \nonumber$$

$$x=6.69 \times 10^{-7} \nonumber$$

Substituting x back into the equilibrium expressions for $\text{Hg}_2^{2+}$ and Cl^– gives their concentrations as

$$\left[\mathrm{Hg}_{2}^{2+}\right]=x=6.7 \times 10^{-7} \ \mathrm{M} \quad\left[\mathrm{Cl}^{-}\right]=2 x=1.3 \times 10^{-6} \ \mathrm{M} \nonumber$$

The molar solubility is equal to [$\text{Hg}_2^{2+}$], or $6.7 \times 10^{-7}$ mol/L.

A More Complex Problem: The Common Ion Effect

Calculating the solubility of Pb(IO₃)₂ in deionized water is a straightforward problem because the solid’s dissolution is the only source of Pb²⁺ and $\text{IO}_3^-$. But what if we add Pb(IO₃)₂ to a solution of 0.10 M Pb(NO₃)₂? Before we set‐up and solve this problem algebraically, think about the system’s chemistry and decide whether the solubility of Pb(IO₃)₂ will increase, decrease, or remain the same. Beginning a problem by thinking about the likely answer is a good habit to develop. Knowing what answers are reasonable will help you spot errors in your calculations and give you more confidence that your solution to a problem is correct. Because the solution already contains a source of Pb²⁺, we can use Le Châtelier’s principle to predict that the solubility of Pb(IO₃)₂ is smaller than that in our previous problem.

We begin by setting up a table to help us keep track of the concentrations of Pb²⁺ and $\text{IO}_3^-$ as this system moves toward and reaches equilibrium.

concentrations	Pb(IO3)2 (s)	$\rightleftharpoons$	Pb^2^+ (aq)	+	2$\text{IO}_3^-$ (aq)
initial	solid		0.10		0
change	solid		+x		+ 2x
equilibrium	solid		0.10 + x		2x

Substituting the equilibrium concentrations into Equation $\ref{6.1}$

$$(0.10+x)(2 x)^{2}=2.5 \times 10^{-13} \nonumber$$

and multiplying out the terms on the equation’s left side leaves us with

$$4 x^{3}+0.40 x^{2}=2.5 \times 10^{-13} \label{6.2}$$

This is a more difficult equation to solve than that for the solubility of Pb(IO₃)₂ in deionized water, and its solution is not immediately obvious. We can find a rigorous solution to Equation $\ref{6.2}$ using computational software packages and spreadsheets, some of which are described in Chapter 6.10.

There are several approaches to solving cubic equations, but none are computationally easy using just paper and pencil.

How might we solve Equation $\ref{6.2}$ if we do not have access to a computer? One approach is to use our understanding of chemistry to simplify the problem. From Le Châtelier’s principle we know that a large initial concentration of Pb²⁺ will decrease significantly the solubility of Pb(IO₃)₂. One reasonable assumption is that the initial concentration of Pb²⁺ is very close to its equilibrium concentration. If this assumption is correct, then the following approximation is reasonable

$$\left[\mathrm{Pb}^{2+}\right]=0.10+x \approx 0.10 \nonumber$$

Substituting this approximation into Equation $\ref{6.1}$ and solving for x gives

$$(0.10)(2 x)^{2}=0.4 x^{2}=2.5 \times 10^{-13} \nonumber$$

$$x=7.91 \times 10^{-7} \nonumber$$

Before we accept this answer, we must verify that our approximation is reasonable. The difference between the actual concentration of Pb²⁺, which is 0.10 + x M, and our assumption that the concentration of Pb²⁺ is 0.10 M is $7.9 \times 10^{-7}$, or $7.9 \times 10^{-4}$ % of the assumed concentration. This is a negligible error. If we accept the result of our calculation, we find that the equilibrium concentrations of Pb²⁺ and $\text{IO}_3^-$ are

$$\left[\mathrm{Pb}^{2+}\right]=0.10+x \approx 0.10 \ \mathrm{M} \text { and }\left[\mathrm{IO}_{3}^{-}\right]=2 x=1.6 \times 10^{-6} \ \mathrm{M} \nonumber$$

$$\begin{aligned} \% \text { error } &=\frac{\text { actual }-\text { assumed }}{\text { assumed }} \times 100 \\ &=\frac{(0.10+x)-0.10}{0.10} \times 100 \\ &=\frac{7.91 \times 10^{-7}}{0.10} \times 100 \\ &=7.91 \times 10^{-4} \% \end{aligned} \nonumber$$

The molar solubility of Pb(IO₃)₂ is equal to the additional concentration of Pb²⁺ in solution, or $7.9 \times 10^{-4}$ mol/L. As expected, we find that Pb(IO₃)₂ is less soluble in the presence of a solution that already contains one of its ions. This is known as the common ion effect.

As outlined in the following example, if an approximation leads to an error that is unacceptably large, then we can extend the process of making and evaluating approximations.

One “rule of thumb” when making an approximation is that it should not introduce an error of more than ±5%. Although this is not an unreasonable choice, what matters is that the error makes sense within the context of the problem you are solving.

Example 6.7.1

Calculate the solubility of Pb(IO₃)₂ in $1.0 \times 10^{-4}$ M Pb(NO₃)₂.

Solution

If we let x equal the change in the concentration of Pb²⁺, then the equilibrium concentrations of Pb²⁺ and $\text{IO}_3^-$ are

$$\left[\mathrm{P} \mathrm{b}^{2+}\right]=1.0 \times 10^{-4}+ \ x \text { and }\left[\mathrm{IO}_{3}^-\right]=2 x \nonumber$$

Substituting these concentrations into Equation $\ref{6.1}$ leaves us with

$$\left(1.0 \times 10^{-4}+ \ x\right)(2 x)^{2}=2.5 \times 10^{-13} \nonumber$$

To solve this equation for x, let’s make the following assumption

$$\left[\mathrm{Pb}^{2+}\right]=1.0 \times 10^{-4}+ \ x \approx 1.0 \times 10^{-4} \ \mathrm{M} \nonumber$$

Solving for x gives its value as $2.50 \times 10^{-5}$; however, when we substitute this value for x back, we find that the calculated concentration of Pb²⁺ at equilibrium

$$\left[\mathrm{Pb}^{2+}\right]=1.0 \times 10^{-4}+ \ x=1.0 \times 10^{-4}+ \ 2.50 \times 10^{-5}=1.25 \times 10^{-4} \ \mathrm{M} \nonumber$$

is 25% greater than our assumption of $1.0 \times 10^{-4}$ M. This error is unreasonably large.

Rather than shouting in frustration, let’s make a new assumption. Our first assumption—that the concentration of Pb²⁺ is $1.0 \times 10^{-4}$ M—was too small. The calculated concentration of $1.25 \times 10^{-4}$ M, therefore, probably is a too large, but closer to the correct concentration than was our first assumption. For our second approximation, let’s assume that

$$\left[\mathrm{Pb}^{2+}\right]=1.0 \times 10^{-4}+ \ x=1.25 \times 10^{-4} \mathrm{M} \nonumber$$

Substituting into Equation $\ref{6.1}$ and solving for x gives its value as $2.24 \times 10^{-5}$. The resulting concentration of Pb²⁺ is

$$\left[\mathrm{Pb}^{2+}\right]=1.0 \times 10^{-4}+ \ 2.24 \times 10^{-5}=1.22 \times 10^{-4} \ \mathrm{M} \nonumber$$

which differs from our assumption of $1.25 \times 10^{-4}$ M by 2.4%. Because the original concentration of Pb²⁺ is given to two significant figure, this is a more reasonable error. Our final solution, to two significant figures, is

$$\left[\mathrm{Pb}^{2+}\right]=1.2 \times 10^{-4} \ \mathrm{M} \text { and }\left[\mathrm{IO}_{3}\right]=4.5 \times 10^{-5} \ \mathrm{M} \nonumber$$

and the molar solubility of Pb(IO₃)₂ is $2.2 \times 10^{-5}$ mol/L. This iterative approach to solving the problems is known as the method of successive approximations.

Exercise 6.7.2

Calculate the molar solubility for Hg₂Cl₂ in 0.10 M NaCl and compare your answer to its molar solubility in deionized water (see Exercise 6.7.1 ).

Answer

We begin by setting up a table to help us keep track of the concentrations $\text{Hg}_2^{2+}$ and Cl^– as this system moves toward and reaches equilibrium.

concentration	Hg2Cl2 (s)	$\rightleftharpoons$	$\text{Hg}_2^{2+}$ (aq)	+	Cl^–(aq)
initial	solid		0		0.10
change	solid		+x		+2x
equilibrium	solid		x		0.1 + 2x

Substituting the equilibrium concentrations into the K_sp expression for Hg₂Cl₂ leaves us with a difficult to solve cubic equation.

$$K_{\mathrm{sp}}=\left[\mathrm{Hg}_{2}^{2+}\right]\left[\mathrm{Cl}^{-}\right]^{2}=(x)(0.10+2 x)^{2}=4 x^{3}+0.40 x^{2}+0.010 x \nonumber$$

Let’s make an assumption to simplify this problem. Because we expect the value of x to be small, let’s assume that

$$\left[\mathrm{Cl}^{-}\right]=0.10+2 x \approx 0.10 \nonumber$$

This simplifies our problem to

$$K_{\mathrm{sp}}=\left[\mathrm{Hg}_{2}^{2+}\right]\left[\mathrm{Cl}^{-}\right]^{2}=(x)(0.10)^{2}=0.010 x=1.2 \times 10^{-18} \nonumber$$

which gives the value of x as $1.2 \times 10^{-16}$ M. The difference between the actual concentration of Cl^–, which is (0.10 + 2x) M, and our assumption that it is 0.10 M introduces an error of $2.4 \times 10^{-13}$ %. This is a negligible error. The molar solubility of Hg₂Cl₂ is the same as the concentration of $\text{Hg}_2^{2+}$, or $1.2 \times 10^{-16}$ M. As expected, the molar solubility in 0.10 M NaCl is less than $6.7 \times 10^{-7}$ mol/L, which is its solubility in water (see solution to Exercise 6.7.1 ).

A Systematic Approach to Solving Equilibrium Problems

Calculating the solubility of Pb(IO₃)₂ in a solution of Pb(NO₃)₂ is more complicated than calculating its solubility in deionized water. The calculation, however, is still relatively easy to organize and the simplifying assumptions are fairly obvious. This problem is reasonably straightforward because it involves only one equilibrium reaction and one equilibrium constant.

Determining the equilibrium composition of a system with multiple equilibrium reactions is more complicated. In this section we introduce a systematic approach to setting‐up and solving equilibrium problems. As shown in Table 6.7.1 , this approach involves four steps.

Table 6.7.1 . Systematic Approach to Solving Equilibrium Problems

Step 1 Write all relevant equilibrium reactions and equilibrium constant expressions.

Step 2 Count the unique species that appear in the equilibrium constant expressions; these are your unknowns. You have enough information to solve the problem if the number of unknowns equals the number of equilibrium constant expressions. If not, add a mass balance equation and/or a charge balance equation. Continue adding equations until the number of equations equals the number of unknowns.

Step 3 Combine your equations and solve for one unknown. Whenever possible, simplify the algebra by making appropriate assumptions. If you make an assumption, set a limit for its error. This decision influences your evaluation of the assumption.

Step 4 Check your assumptions. If any assumption proves invalid, return to the previous step and continue solving. The problem is complete when you have an answer that does not violate any of your assumptions.

In addition to equilibrium constant expressions, two other equations are important to this systematic approach to solving an equilibrium problem. The first of these equations is a mass balance equation, which simply is a statement that matter is conserved during a chemical reaction. In a solution of acetic acid, for example, the combined concentrations of the conjugate weak acid, CH₃COOH, and the conjugate weak base, CH₃COO^–, must equal acetic acid’s initial concentration, $C_{\text{CH}_3\text{COOH}}$.

$$C_{\mathrm{CH}_{\mathrm{3}} \mathrm{COOH}}=\left[\mathrm{CH}_{3} \mathrm{COOH}\right]+\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right] \nonumber$$

You may recall from Chapter 2 that this is the difference between a formal concentration and a molar concentration. The variable C represents a formal concentration.

The second equation is a charge balance equation, which requires that the total positive charge from the cations equal the total negative charge from the anions. Mathematically, the charge balance equation is

$$\sum_{i=1}^{n}\left(z^{+}\right)_{i}\left[{C^{z}}^+\right]_{i} = -\sum_{j=1}^{m}(z^-)_{j}\left[{A^{z}}^-\right]_{j} \nonumber$$

where [C^z+]_i and [A^z-]_j are, respectively, the concentrations of the i^th cation and the j^th anion, and (z⁺)_i and (z^–)_j are the charges for the i^th cation and the j^th anion. Every ion in solution, even if it does not appear in an equilibrium reaction, must appear in the charge balance equation. For example, the charge balance equation for an aqueous solution of Ca(NO₃)₂ is

$$2 \times\left[\mathrm{Ca}^{2+}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{+}\right]+\left[\mathrm{NO}_{3}^-\right] \nonumber$$

Note that we multiply the concentration of Ca²⁺ by two and that we include the concentrations of H₃O⁺ and OH^–.

A charge balance is a conservation of a charge. The minus sign in front of the summation term on the right side of the charge balance equation ensures that both summations are positive. There are situations where it is impossible to write a charge balance equation because we do not have enough information about the solution’s composition. For example, suppose we fix a solution’s pH using a buffer. If the buffer’s composition is not specified, then we cannot write a charge balance equation.

Example 6.7.2

Write mass balance equations and a charge balance equation for a 0.10 M solution of NaHCO₃.

Solution

It is easier to keep track of the species in solution if we write down the reactions that define the solution’s composition. These reactions are the dissolution of a soluble salt

$$\mathrm{NaHCO}_{3}(s) \rightarrow \mathrm{Na}^{+}(a q)+\mathrm{HCO}_{3}^{-}(a q) \nonumber$$

and the acid–base dissociation reactions of $\text{HCO}_3^-$ and H₂O

$$\mathrm{HCO}_{3}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{CO}_{3}^{2-}(a q) \nonumber$$

$$\mathrm{HCO}_{3}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{H}_{2} \mathrm{CO}_{3}(a q) \nonumber$$

$$2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber$$

The mass balance equations are

$$0.10 \mathrm{M}=\left[\mathrm{H}_{2} \mathrm{CO}_{3}\right]+\left[\mathrm{HCO}_{3}^{-}\right]+\left[\mathrm{CO}_{3}^{2-}\right] \nonumber$$

$$0.10 \ \mathrm{M}=\left[\mathrm{Na}^{+}\right] \nonumber$$

and the charge balance equation is

$$\left[\mathrm{Na}^{+}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{-}\right]+\left[\mathrm{HCO}_{3}^-\right]+2 \times\left[\mathrm{CO}_{3}^{2-}\right] \nonumber$$

Exercise 6.7.3

Write appropriate mass balance and charge balance equations for a solution containing 0.10 M KH₂PO₄ and 0.050 M Na₂HPO₄.

Answer

To help us determine what ions are in solution, let’s write down all the reaction needed to prepare the solutions and the equilibrium reactions that take place within these solutions. These reactions are the dissolution of two soluble salts

$$\mathrm{KH}_{2} \mathrm{PO}_{4}(s) \longrightarrow \mathrm{K}^{+}(a q)+\mathrm{H}_{2} \mathrm{PO}_{4}^{-}(a q) \nonumber$$

$$\mathrm{NaHPO}_{4}(s) \longrightarrow \mathrm{Na}^{+}(a q)+\mathrm{HPO}_{4}^{2-}(a q) \nonumber$$

and the acid–base dissociation reactions for $\text{H}_2\text{PO}_4^-$, $\text{HPO}_4^{2-}$. and H₂O.

$$\mathrm{H}_{2} \mathrm{PO}_{4}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons\mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{HPO}_{4}^{2-}(a q) \nonumber$$

$$\mathrm{H}_{2} \mathrm{PO}_{4}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{H}_{3} \mathrm{PO}_{4}(a q) \nonumber$$

$$\mathrm{HPO}_{4}^{2-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{PO}_{4}^{3-}(a q) \nonumber$$

$$2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber$$

Note that we did not include the base dissociation reaction for $\text{HPO}_4^{2-}$ because we already accounted for its product, $\text{H}_2\text{PO}_4^-$, in another reaction. The mass balance equations for K⁺ and Na⁺ are straightforward

$$\left[\mathrm{K}^{+}\right]=0.10 \ \mathrm{M} \text { and }\left[\mathrm{Na}^{+}\right]=0.10 \ \mathrm{M} \nonumber$$

but the mass balance equation for phosphate takes a bit more thought. Both $\text{H}_2\text{PO}_4^-$ and $\text{HPO}_4^{2-}$ produce the same ions in solution. We can, therefore, imagine that the solution initially contains 0.15 M KH₂PO₄, which gives the following mass balance equation.

$$\left[\mathrm{H}_{3} \mathrm{PO}_{4}\right]+\left[\mathrm{H}_{2} \mathrm{PO}_{4}^-\right]+\left[\mathrm{HPO}_{4}^{2-}\right]+\left[\mathrm{PO}_{4}^{3-}\right]=0.15 \ \mathrm{M} \nonumber$$

The charge balance equation is

$$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]+\left[\mathrm{K}^{+}\right]+\left[\mathrm{Na}^{+}\right] =\left[\mathrm{H}_{2} \mathrm{PO}_{4}^{-}\right]+2 \times\left[\mathrm{HPO}_{4}^{2-}\right] +3 \times\left[\mathrm{PO}_{4}^{3-}\right]+\left[\mathrm{OH}^{-}\right] \nonumber$$

pH of a Monoprotic Weak Acid

To illustrate the systematic approach to solving equilibrium problems, let’s calculate the pH of 1.0 M HF. Two equilibrium reactions affect the pH. The first, and most obvious, is the acid dissociation reaction for HF

$$\mathrm{HF}(a q)+\mathrm{H}_{2} \mathrm{O}(l) \rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{F}^{-}(a q) \nonumber$$

for which the equilibrium constant expression is

$$K_{\mathrm{a}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{F}^{-}\right]}{[\mathrm{HF}]}=6.8 \times 10^{-4} \label{6.3}$$

The second equilibrium reaction is the dissociation of water, which is an obvious yet easily neglected reaction

$$2 \mathrm{H}_{2} \mathrm{O}(l) \rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber$$

$$K_{w}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=1.00 \times 10^{-14} \label{6.4}$$

Counting unknowns, we find four: [HF], [F^–], [H₃O⁺], and [OH^–]. To solve this problem we need two additional equations. These equations are a mass balance equation on hydrofluoric acid

$$C_{\mathrm{HF}}=[\mathrm{HF}]+\left[\mathrm{F}^{-}\right]=1.0 \mathrm{M} \label{6.5}$$

and a charge balance equation

$$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{-}\right]+\left[\mathrm{F}^{-}\right] \label{6.6}$$

With four equations and four unknowns, we are ready to solve the problem. Before doing so, let’s simplify the algebra by making two assumptions.

Assumption One. Because HF is a weak acid, we know that the solution is acidic. For an acidic solution it is reasonable to assume that

$$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]>>\left[\mathrm{OH}^{-}\right] \nonumber$$

which simplifies the charge balance equation to

$$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{F}^{-}\right] \label{6.7}$$

Assumption Two. Because HF is a weak acid, very little of it dissociates to form F^–. Most of the HF remains in its conjugate weak acid form and it is reasonable to assume that

$$[\mathrm{HF}]>>\left[\mathrm{F}^{-}\right] \nonumber$$

which simplifies the mass balance equation to

$$C_{\mathrm{HF}}=[\mathrm{HF}]=1.0 \ \mathrm{M} \label{6.8}$$

For this exercise let’s accept an assumption if it introduces an error of less than ±5%.

Substituting Equation $\ref{6.7}$ and Equation $\ref{6.8}$ into Equation $\ref{6.3}$, and solving for the concentration of H₃O⁺ gives us

$$\mathrm{K}_{\mathrm{a}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{F}^{-}\right]}{[\mathrm{HF}]}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\mathrm{C}_{\mathrm{HF}}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{2}}{\mathrm{C}_{\mathrm{HF}}}=6.8 \times 10^{-4} \nonumber$$

$$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\sqrt{K_{\mathrm{a}} C_{\mathrm{HF}}}=\sqrt{\left(6.8 \times 10^{-4}\right)(1.0)}=2.6 \times 10^{-2} \nonumber$$

Before accepting this answer, we must verify our assumptions. The first assumption is that [OH^–] is significantly smaller than [H₃O⁺]. Using Equation $\ref{6.4}$, we find that

$$\left[\mathrm{OH}^{-}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}=\frac{1.00 \times 10^{-14}}{2.6 \times 10^{-2}}=3.8 \times 10^{-13} \nonumber$$

Clearly this assumption is acceptable. The second assumption is that [F^–] is significantly smaller than [HF]. From Equation $\ref{6.7}$ we have

$$\left[\mathrm{F}^{-}\right]=2.6 \times 10^{-2} \ \mathrm{M} \nonumber$$

Because [F^–] is 2.60% of C_HF, this assumption also is acceptable. Given that [H₃O⁺] is $2.6 \times 10^{-2}$ M, the pH of 1.0 M HF is 1.59.

How does the calculation change if we require that the error introduced in our assumptions be less than ±1%? In this case we no longer can assume that [HF] >> [F^–] and we cannot simplify the mass balance equation. Solving the mass balance equation for [HF]

$$[\mathrm{HF}]=C_{\mathrm{HF}}-\left[\mathrm{F}^{-}\right]=C_{\mathrm{HF}}-\left[\mathrm{H}_{3} \mathrm{O}^{+}\right] \nonumber$$

and substituting into the K_a expression along with Equation $\ref{6.7}$ gives

$$K_{\mathrm{a}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{2}}{C_{\mathrm{HF}}-\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]} \nonumber$$

Rearranging this equation leaves us with a quadratic equation

$$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{2}+K_{\mathrm{a}}\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]-K_{\mathrm{a}} C_{\mathrm{HF}}=0 \nonumber$$

which we solve using the quadratic formula

$$x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a} \nonumber$$

where a, b, and c are the coefficients in the quadratic equation

$$a x^{2}+b x+c=0 \nonumber$$

Solving a quadratic equation gives two roots, only one of which has chemical significance. For our problem, the equation’s roots are

$$x=\frac{-6.8 \times 10^{-4} \pm \sqrt{\left(6.8 \times 10^{-4}\right)^{2}-(4)(1)\left(-6.8 \times 10^{-4}\right)}}{(2)(1)} \nonumber$$

$$x=\frac{-6.8 \times 10^{-4} \pm 5.22 \times 10^{-2}}{2} \nonumber$$

$$x=2.57 \times 10^{-2} \text { or }-2.64 \times 10^{-2} \nonumber$$

Only the positive root is chemically significant because the negative root gives a negative concentration for H₃O⁺. Thus, [H₃O⁺] is $2.57 \times 10^{-2}$ M and the pH is 1.59.

You can extend this approach to calculating the pH of a monoprotic weak base by replacing K_a with K_b, replacing C_HF with the weak base’s concentration, and solving for [OH^–] in place of [H₃O⁺].

Exercise 6.7.4

Calculate the pH of 0.050 M NH₃. State any assumptions you make in solving the problem, limiting the error for any assumption to ±5%. The K_b value for NH₃ is $1.75 \times 10^{-5}$.

Answer

To determine the pH of 0.050 M NH₃, we need to consider two equilibrium reactions: the base dissociation reaction for NH₃

$$\mathrm{NH}_{3}(a q)+\mathrm{H}_{2} \mathrm{O}(l) \rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{NH}_{4}^{+}(a q) \nonumber$$

and water’s dissociation reaction.

$$2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber$$

These two reactions contain four species whose concentrations we need to consider: NH₃, $\text{NH}_4^+$, H₃O⁺, and OH^–. We need four equations to solve the problem—these equations are the K_b equation for NH₃

$$K_{\mathrm{b}}=\frac{\left[\mathrm{NH}_{4}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{NH}_{3}\right]}=1.75 \times 10^{-5} \nonumber$$

the K_w equation for H₂O

$$K_{w}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right] \nonumber$$

a mass balance equation on ammonia

$$C_{\mathrm{NH}_{3}}=0.050 \ \mathrm{M}=\left[\mathrm{NH}_{3}\right]+\left[\mathrm{NH}_{4}^{+}\right] \nonumber$$

and a charge balance equation

$$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]+\left[\mathrm{NH}_{4}^{+}\right]=\left[\mathrm{OH}^{-}\right] \nonumber$$

To solve this problem, we will make two assumptions. Because NH₃ is a base, our first assumption is

$$\left[\mathrm{OH}^{-}\right]>>\left[\mathrm{H}_{3} \mathrm{O}^{+}\right] \nonumber$$

which simplifies the charge balance equation to

$$\left[\mathrm{NH}_{4}^{+}\right]=\left[\mathrm{OH}^{-}\right] \nonumber$$

Because NH₃ is a weak base, our second assumption is

$$\left[\mathrm{NH}_{3}\right]>>\left[\mathrm{NH}_{4}^{+}\right] \nonumber$$

which simplifies the mass balance equation to

$$C_{\mathrm{NH}_{3}}=0.050 \ \mathrm{M}=\left[\mathrm{NH}_{3}\right] \nonumber$$

Substituting the simplified charge balance equation and mass balance equation into the K_b equation leave us with

$$K_{\mathrm{b}}=\frac{\left[\mathrm{NH}_{4}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{NH}_{3}\right]}=\frac{\left[\mathrm{OH}^{-}\right]\left[\mathrm{OH}^{-}\right]}{C_{\mathrm{NH}_3}}=\frac{\left[\mathrm{OH}^{-}\right]^{2}}{C_{\mathrm{NH_3}}}=1.75 \times 10^{-5} \nonumber$$

$$\left[\mathrm{OH}^{-}\right]=\sqrt{K_{\mathrm{b}} C_{\mathrm{NH_3}}}=\sqrt{\left(1.75 \times 10^{-5}\right)(0.050)}=9.35 \times 10^{-4} \nonumber$$

Before we accept this answer, we must verify our two assumptions. The first assumption is that the concentration of OH^– is significantly greater than the concentration of H₃O⁺. Using K_w, we find that

$$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{OH}^{-}\right]}=\frac{1.00 \times 10^{-14}}{9.35 \times 10^{-4}}=1.07 \times 10^{-11} \nonumber$$

Clearly this assumption is acceptable. Our second assumption is that the concentration of NH₃ is significantly greater than the concentration of $\text{NH}_4^+$. Using our simplified charge balance equation, we find that

$$\left[\mathrm{NH}_{4}^{+}\right]=\left[\mathrm{OH}^{-}\right]=9.35 \times 10^{-4} \nonumber$$

Because the concentration of $\text{NH}_4^+$ is 1.9% of $C_{\text{NH}_3}$, our second assumption also is reasonable. Given that [H₃O⁺] is $1.07 \times 10^{-11}$, the pH is 10.97.

pH of a Polyprotic Acid or Base

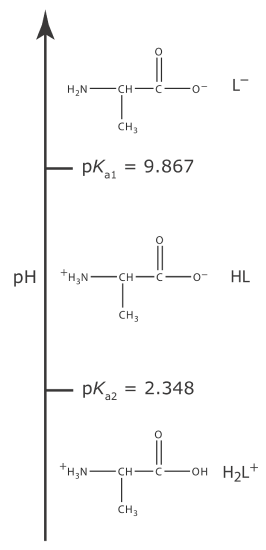
A more challenging problem is to find the pH of a solution that contains a polyprotic weak acid or one of its conjugate species. As an example, consider the amino acid alanine, whose structure is shown in Figure 6.7.1 . The ladder diagram in Figure 6.7.2 shows alanine’s three acid–base forms and their respective areas of predominance. For simplicity, we identify these species as H₂L⁺, HL, and L^–.

Figure 6.7.1 . Structure of the amino acid alanine, which has pKa values of 2.348 (–COOH) and 9.867 (–NH2).

Figure 6.7.2 . Ladder diagram for alanine.

pH of 0.10 M Alanine Hydrochloride (H₂L⁺)

Alanine hydrochloride is the salt of the diprotic weak acid H₂L⁺ and Cl^–. Because H₂L⁺ has two acid dissociation reactions, a complete systematic solution to this problem is more complicated than that for a monoprotic weak acid. The ladder diagram in Figure 6.7.2 helps us simplify the problem. Because the areas of predominance for H₂L⁺ and L^– are so far apart, we can assume that a solution of H₂L⁺ will not contain a significant amount of L^–. As a result, we can treat H₂L⁺ as though it is a monoprotic weak acid. Calculating the pH of 0.10 M alanine hydrochloride, which is 1.72, is left to the reader as an exercise.

pH of 0.10 M Sodium Alaninate (L^–)

The alaninate ion is a diprotic weak base. Because L^– has two base dissociation reactions, a complete systematic solution to this problem is more complicated than that for a monoprotic weak base. Once again, the ladder diagram in Figure 6.7.2 helps us simplify the problem. Because the areas of predominance for H₂L⁺ and L^– are so far apart, we can assume that a solution of L^– will not contain a significant amount of H₂L⁺. As a result, we can treat L^– as though it is a monoprotic weak base. Calculating the pH of 0.10 M sodium alaninate, which is 11.42, is left to the reader as an exercise.

pH of 0.10 M Alanine (HL)

Finding the pH of a solution of alanine is more complicated than our previous two examples because we cannot ignore the presence of either H₂L⁺ or L^–. To calculate the solution’s pH we must consider alanine’s acid dissociation reaction

$$\mathrm{HL}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{L}^{-}(a q) \nonumber$$

and its base dissociation reaction

$$\mathrm{HL}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{H}_{2} \mathrm{L}^{+}(a q) \nonumber$$

and, as always, we must also consider the dissociation of water

$$2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber$$

This leaves us with five unknowns—[H₂L⁺], [HL], [L^–], [H₃O⁺], and [OH^–]—for which we need five equations. These equations are K_a2 and K_b2 for alanine

$$K_{\mathrm{a} 2}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{L}^{-}\right]}{[\mathrm{HL}]} \nonumber$$

$$K_{\mathrm{b} 2}=\frac{K_{\mathrm{w}}}{K_{\mathrm{a1}}}=\frac{\left[\mathrm{OH}^{-}\right]\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]}{[\mathrm{HL}]} \nonumber$$

the K_w equation

$$K_{\mathrm{w}}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right] \nonumber$$

a mass balance equation for alanine

$$C_{\mathrm{HL}}=\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]+[\mathrm{HL}]+[\mathrm{L}^{-}] \nonumber$$

and a charge balance equation

$$\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=[\mathrm{OH}^-]+[\mathrm{L^-}] \nonumber$$

Because HL is a weak acid and a weak base, it seems reasonable to assume that little of it will dissociate and that

$$[\mathrm{HL}]>>\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]+[\mathrm{L}^-] \nonumber$$

which allows us to simplify the mass balance equation to

$$C_{\mathrm{HL}}=[\mathrm{HL}] \nonumber$$

Next we solve K_b2 for [H₂L⁺]

$$\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]=\frac{K_{\mathrm{w}}[\mathrm{HL}]}{K_{\mathrm{a1}}\left[\mathrm{OH}^{-}\right]}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right][\mathrm{HL}]}{K_{\mathrm{a1}}}=\frac{C_{\mathrm{HL}}\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{K_{\mathrm{a1}}} \nonumber$$

and solve K_a2 for [L^–]

$$[\mathrm{L^-}]=\frac{K_{a2}[\mathrm{HL}]}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}=\frac{K_{a2} C_{\mathrm{HL}}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]} \nonumber$$

Substituting these equations for [H₂L⁺] and [L^–], and the equation for K_w, into the charge balance equation give us

$$\frac{C_{\mathrm{HL}}\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{K_{\mathrm{a1}}}+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\frac{K_{\mathrm{w}}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}+\frac{K_{a2} C_{\mathrm{HL}}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]} \nonumber$$

which we simplify to

$$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left(\frac{C_{\mathrm{HL}}}{K_{\mathrm{a1}}}+1\right)=\frac{1}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}\left(K_{\mathrm{w}}+K_{a2} C_{\mathrm{HL}}\right) \nonumber$$

$$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{2}=\frac{\left(K_{\mathrm{a} 2} C_{\mathrm{HL}}+K_{\mathrm{w}}\right)}{\frac{C_{\mathrm{HL}}}{K_{\mathrm{a1}}}+1}=\frac{K_{\mathrm{a1}}\left(K_{\mathrm{a2}} C_{\mathrm{HL}}+K_{\mathrm{w}}\right)}{C_{\mathrm{HL}}+K_{\mathrm{a1}}} \nonumber$$

$$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\sqrt{\frac{\left(K_{\mathrm{a1}} K_{a2} C_{\mathrm{HL}}+K_{\mathrm{a1}} K_{\mathrm{w}}\right)}{C_{\mathrm{HL}}+K_{\mathrm{a1}}}} \nonumber$$

We can further simplify this equation if K_a1K_w << K_a1K_a2C_HL, and if K_a1 << C_HL, leaving us with

$$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\sqrt{K_{\mathrm{a1}} K_{\mathrm{a} 2}} \nonumber$$

For a solution of 0.10 M alanine the [H₃O⁺] is

$$\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\sqrt{\left(4.487 \times 10^{-3}\right)\left(1.358 \times 10^{-10}\right)}=7.806 \times 10^{-7} \ \mathrm{M} \nonumber$$

or a pH of 6.11.

Exercise 6.7.5

Verify that each assumption in our solution for the pH of 0.10 M alanine is reasonable, using ±5% as the limit for the acceptable error.

Answer

In solving for the pH of 0.10 M alanine, we made the following three assumptions: (a) [HL] >> [H₂L⁺] + [L^–]; (b) K_a1K_w << K_a1K_a2C_HL; and (c) K_a1 << C_HL. Assumptions (b) and (c) are easy to check. The value of K_a1 ($4.487 \times 10^{-3}$) is 4.5% of C_HL (0.10), and K_a1Kw ($4.487 \times 10^{-17}$) is 0.074% of K_a1K_a2C_HL ($6.093 \times 10^{-14}$). Each of these assumptions introduces an error of less than ±5%.

To test assumption (a) we need to calculate the concentrations of H₂L⁺ and L^–, which we accomplish using the equations for K_a1 and K_a2.

$$\left[\mathrm{H}_{2} \mathrm{L}^{+}\right]=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right][\mathrm{HL}]}{K_{\mathrm{a1}}}=\frac{\left(7.807 \times 10^{-7}\right)(0.10)}{4.487 \times 10^{-3}}=1.74 \times 10^{-5} \nonumber$$

$$\left[\mathrm{L}^{-}\right]=\frac{K_{a 2}[\mathrm{HL}]}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}=\frac{\left(1.358 \times 10^{-10}\right)(0.10)}{7.807 \times 10^{-7}}=1.74 \times 10^{-5} \nonumber$$

Because these concentrations are less than ±5% of CHL, the first assumption also is acceptable.

Effect of Complexation on Solubility

One method for increasing a precipitate’s solubility is to add a ligand that forms soluble complexes with one of the precipitate’s ions. For example, the solubility of AgI increases in the presence of NH₃ due to the formation of the soluble $\text{Ag(NH}_3)_2^+$ complex. As a final illustration of the systematic approach to solving equilibrium problems, let’s calculate the molar solubility of AgI in 0.10 M NH₃.

We begin by writing the relevant equilibrium reactions, which includes the solubility of AgI, the acid–base chemistry of NH₃ and H₂O, and the metal‐ligand complexation chemistry between Ag⁺ and NH₃.

$$\begin{array}{c}{\operatorname{AgI}(s)\rightleftharpoons\operatorname{Ag}^{+}(a q)+\mathrm{I}^{-}(a q)} \\ {\mathrm{NH}_{3}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{NH}_{4}^{+}(a q)} \\ {2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q)} \\ {\mathrm{Ag}^{+}(a q)+2 \mathrm{NH}_{3}(a q) \rightleftharpoons \mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}(a q)}\end{array} \nonumber$$

This leaves us with seven unknowns—[Ag⁺], [I^–], [NH₃], [$\text{NH}_4^+$ ], [OH^–], [H₃O⁺], and [$\text{Ag(NH}_3)_2^+$]—and a need for seven equations. Four of the equations we need to solve this problem are the equilibrium constant expressions

$$K_{\mathrm{sp}}=\left[\mathrm{Ag}^{+}\right]\left[\mathrm{I}^{-}\right]=8.3 \times 10^{-17} \label{6.9}$$

$$K_{\mathrm{b}}=\frac{\left[\mathrm{NH}_{4}^{+}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{NH}_{3}\right]}=1.75 \times 10^{-5} \label{6.10}$$

$$K_{\mathrm{w}}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=1.00 \times 10^{-14} \label{6.11}$$

$$\beta_{2}=\frac{\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]}{\left[\mathrm{Ag}^{+}\right]\left[\mathrm{NH}_{3}\right]^{2}}=1.7 \times 10^{7} \label{6.12}$$

We still need three additional equations. The first of these equations is a mass balance for NH₃.

$$C_{\mathrm{NH}_{3}}=\left[\mathrm{NH}_{3}\right]+\left[\mathrm{NH}_{4}^{+}\right]+2 \times\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right] \label{6.13}$$

In writing this mass balance equation we multiply the concentration of $\text{Ag(NH}_3)_2^+$ by two since there are two moles of NH₃ per mole of $\text{Ag(NH}_3)_2^+$. The second additional equation is a mass balance between iodide and silver. Because AgI is the only source of I^– and Ag⁺, each iodide in solution must have an associated silver ion, which may be Ag⁺ or $\text{Ag(NH}_3)_2^+$ ; thus

$$\left[\mathrm{I}^{-}\right]=\left[\mathrm{Ag}^{+}\right]+\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right] \label{6.14}$$

Finally, we include a charge balance equation.

$$\left[\mathrm{Ag}^{+}\right]+\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]+\left[\mathrm{NH}_{4}^{+}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=[\mathrm{OH}^-]+[\mathrm{I}^-] \label{6.15}$$

Although the problem looks challenging, three assumptions greatly simplify the algebra.

Assumption One. Because the formation of the $\text{Ag(NH}_3)_2^+$ complex is so favorable ($\beta_2$ is $1.7 \times 10^7$), there is very little free Ag⁺ in solution and it is reasonable to assume that

$$\left[\mathrm{Ag}^{+}\right]<<\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right] \nonumber$$

Assumption Two. Because NH₃ is a weak base we may reasonably assume that most uncomplexed ammonia remains as NH₃; thus

$$\left[\mathrm{NH}_{4}^{+}\right]<<\left[\mathrm{NH}_{3}\right] \nonumber$$

Assumption Three. Because K_sp for AgI is significantly smaller than $\beta_2$ for $\text{Ag(NH}_3)_2^+$, the solubility of AgI probably is small enough that very little ammonia is needed to form the metal–ligand complex; thus

$$\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]<<\left[\mathrm{NH}_{3}\right] \nonumber$$

As we use these assumptions to simplify the algebra, let’s set ±5% as the limit for error.

Assumption two and assumption three suggest that the concentration of NH₃ is much larger than the concentrations of either $\text{NH}_4^+$ or $\text{Ag(NH}_3)_2^+$, which allows us to simplify the mass balance equation for NH₃ to

$$C_{\mathrm{NH}_{3}}=\left[\mathrm{NH}_{3}\right] \label{6.16}$$

Finally, using assumption one, which suggests that the concentration of $\text{Ag(NH}_3)_2^+$ is much larger than the concentration of Ag⁺, we simplify the mass balance equation for I^– to

$$\left[\mathrm{I}^{-}\right]=\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right] \label{6.17}$$

Now we are ready to combine equations and to solve the problem. We begin by solving Equation $\ref{6.9}$ for [Ag⁺] and substitute it into $\beta_2$ (Equation $\ref{6.12}$), which leaves us with

$$\beta_{2}=\frac{\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right][\mathrm{I}^-]}{K_{\mathrm{sp}}\left[\mathrm{NH}_{3}\right]^{2}} \label{6.18}$$

Next we substitute Equation $\ref{6.16}$ and Equation $\ref{6.17}$ into Equation $\ref{6.18}$, obtaining

$$\beta_{2}=\frac{\left[\mathrm{I}^{-}\right]^{2}}{K_{\mathrm{sp}}\left(C_{\mathrm{NH}_3}\right)^{2}} \label{6.19}$$

Solving Equation $\ref{6.19}$ for [I^–] gives

$$\left[\mathrm{I}^{-}\right]=C_{\mathrm{NH}_3} \sqrt{\beta_{2} K_{s p}} = \\ (0.10) \sqrt{\left(1.7 \times 10^{7}\right)\left(8.3 \times 10^{-17}\right)}=3.76 \times 10^{-6} \ \mathrm{M} \nonumber$$

Because one mole of AgI produces one mole of I^–, the molar solubility of AgI is the same as the [I^–], or $3.8 \times 10^{-6}$ mol/L.

Before we accept this answer we need to check our assumptions. Substituting [I^–] into Equation $\ref{6.9}$, we find that the concentration of Ag⁺ is

$$\left[\mathrm{Ag}^{+}\right]=\frac{K_{\mathrm{p}}}{[\mathrm{I}^-]}=\frac{8.3 \times 10^{-17}}{3.76 \times 10^{-6}}=2.2 \times 10^{-11} \ \mathrm{M} \nonumber$$

Substituting the concentrations of I^– and Ag+ into the mass balance equation for iodide (Equation $\ref{6.14}$), gives the concentration of $\text{Ag(NH}_3)_2^+$ as

$$\left[\operatorname{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]=[\mathrm{I}^-]-\left[\mathrm{Ag}^{+}\right]=3.76 \times 10^{-6}-2.2 \times 10^{-11}=3.76 \times 10^{-6} \ \mathrm{M} \nonumber$$

Our first assumption that [Ag⁺] is significantly smaller than the [$\text{Ag(NH}_3)_2^+$] is reasonable.

Substituting the concentrations of Ag⁺ and $\text{Ag(NH}_3)_2^+$ into Equation $\ref{6.12}$ and solving for [NH₃], gives

$$\left[\mathrm{NH}_{3}\right]=\sqrt{\frac{\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]}{\left[\mathrm{Ag}^{+}\right] \beta_{2}}}=\sqrt{\frac{3.76 \times 10^{-6}}{\left(2.2 \times 10^{-11}\right)\left(1.7 \times 10^{7}\right)}}=0.10 \ \mathrm{M} \nonumber$$

From the mass balance equation for NH3 (Equation $\ref{6.12}$) we see that [$\text{NH}_4^+$] is negligible, verifying our second assumption that $[\text{NH}_4^+]$ is significantly smaller than [NH₃]. Our third assumption that [$\text{Ag(NH}_3)_2^+$] is significantly smaller than [NH₃] also is reasonable.

Did you notice that our solution to this problem did not make use of Equation $\ref{6.15}$, the charge balance equation? The reason for this is that we did not try to solve for the concentration of all seven species. If we need to know the reaction mixture’s complete composition at equilibrium, then we will need to incorporate the charge balance equation into our solution.