6.4: Equilibrium Constants for Chemical Reactions

Several types of chemical reactions are important in analytical chemistry, either in preparing a sample for analysis or during the analysis. The most significant of these are precipitation reactions, acid–base reactions, complexation reactions, and oxidation–reduction reactions. In this section we review these reactions and their equilibrium constant expressions.

Another common name for an oxidation–reduction reaction is a redox reaction, where “red” is short for reduction and “ox” is short for oxidation.

Precipitation Reactions

In a precipitation reaction, two or more soluble species combine to form an insoluble precipitate. The most common precipitation reaction is a metathesis reaction in which two soluble ionic compounds exchange parts. For example, if we add a solution of lead nitrate, Pb(NO₃)₂, to a solution of potassium chloride, KCl, a precipitate of lead chloride, PbCl₂, forms. We usually write a precipitation reaction as a net ionic equation, which shows only the precipitate and those ions that form the precipitate; thus, the precipitation reaction for PbCl₂ is

\[\mathrm{Pb}^{2+}(a q)+2 \mathrm{Cl}^{-}(a q) \rightleftharpoons \mathrm{PbCl}_{2}(s) \nonumber\]

When we write the equilibrium constant for a precipitation reaction, we focus on the precipitate’s solubility; thus, for PbCl₂, the solubility reaction is

\[\mathrm{PbCl}_{2}(s)\rightleftharpoons \mathrm{Pb}^{2+}(a q)+2 \mathrm{Cl}^{-}(a q) \nonumber\]

and its equilibrium constant, or solubility product, K_sp, is

\[K_{\mathrm{sp}}=\left[\mathrm{Pb}^{2+}\right]\left[\mathrm{Cl}^{-}\right]^{2} \label{6.1}\]

Even though it does not appear in the K_sp expression, it is important to remember that Equation \ref{6.1} is valid only if PbCl₂(s) is present and in equilibrium with Pb²⁺ and Cl^–. You will find values for selected solubility products in Appendix 10.

Acid–Base Reactions

A useful definition of acids and bases is that independently introduced in 1923 by Johannes Brønsted and Thomas Lowry. In the Brønsted‐Lowry definition, an acid is a proton donor and a base is a proton acceptor. Note the connection between these definitions—defining a base as a proton acceptor implies there is an acid available to donate the proton. For example, in reaction \ref{6.2} acetic acid, CH₃COOH, donates a proton to ammonia, NH₃, which serves as the base.

\[\mathrm{CH}_{3} \mathrm{COOH}(aq)+\mathrm{NH}_{3}(aq) \rightleftharpoons \mathrm{NH}_{4}^{+}(aq)+\mathrm{CH}_{3} \mathrm{COO}^{-}(aq) \label{6.2}\]

When an acid and a base react, the products are a new acid and a new base. For example, the acetate ion, CH₃COO^–, in reaction \ref{6.2} is a base that can accept a proton from the acidic ammonium ion, \(\text{NH}_4^+\), forming acetic acid and ammonia. We call the acetate ion the conjugate base of acetic acid, and we call the ammonium ion the conjugate acid of ammonia.

Strong and Weak Acids

The reaction of an acid with its solvent (typically water) is an acid dissociation reaction. We divide acids into two categories—strong and weak—based on their ability to donate a proton to the solvent. A strong acid, such as HCl, almost completely transfers its proton to the solvent, which acts as the base.

\[\mathrm{HCl}(a q)+\mathrm{H}_{2} \mathrm{O}(l) \rightarrow \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{Cl}^{-}(a q) \nonumber\]

We use a single arrow (\(\rightarrow\)) in place of the equilibrium arrow (\(\rightleftharpoons\)) because we treat HCl as if it dissociates completely in an aqueous solution. In water, the common strong acids are hydrochloric acid (HCl), hydroiodic acid (HI), hydrobromic acid (HBr), nitric acid (HNO₃), perchloric acid (HClO₄), and the first proton of sulfuric acid (H₂SO₄).

The strength of an acid is a function of the acid and the solvent. For example, HCl does not act as a strong acid in methanol. In this case we use the equilibrium arrow when writing the acid–base reaction.

\[\mathrm{HCl}+\mathrm{CH}_{3} \mathrm{OH}\rightleftharpoons \mathrm{CH}_{3} \mathrm{OH}_{2}^{+}+\mathrm{Cl}^{-} \nonumber\]

A weak acid, of which aqueous acetic acid is one example, does not completely donate its acidic proton to the solvent. Instead, most of the acid remains undissociated with only a small fraction present as the conjugate base.

\[\mathrm{CH}_{3} \mathrm{COOH}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{CH}_{3} \mathrm{COO}^{-}(a q) \nonumber\]

The equilibrium constant for this reaction is an acid dissociation constant, K_a, which we write as

\[K_{a}=\frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]}=1.75 \times 10^{-5} \nonumber\]

The magnitude of K provides information about a weak acid's relative strength, with a smaller K_a corresponding to a weaker acid. The ammonium ion, \(\text{NH}_4^+\), for example, has a K_a of \(5.702 \times 10^{-10}\) and is a weaker acid than acetic acid.

Earlier we noted that we omit pure solids and pure liquids from equilibrium constant expressions. Because the solvent, H₂O, is not pure, you might wonder why we have not included it in acetic acid’s K_a expression. Recall that we divide each term in an equilibrium constant expression by its standard state value. Because the concentration of H₂O is so large—it is approximately 55.5 mol/L—its concentration as a pure liquid and as a solvent are virtually identical. The ratio

\[\frac{\left[\mathrm{H}_{2} \mathrm{O}\right]}{\left[\mathrm{H}_{2} \mathrm{O}\right]^{\circ}} \nonumber\]

is essentially 1.00.

A monoprotic weak acid, such as acetic acid, has only a single acidic proton and a single acid dissociation constant. Other acids, such as phosphoric acid, have multiple acidic protons, each characterized by an acid dissociation constant. We call such acids polyprotic. Phosphoric acid, for example, has three acid dissociation reactions and three acid dissociation constants.

\[\mathrm{H}_{3} \mathrm{PO}_{4}(a q)+\mathrm{H}_{2} \mathrm{O}(l) \rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{H}_{2} \mathrm{PO}_{4}^{-}(a q) \nonumber\]

\[K_{\mathrm{al}}=\frac{\left[\mathrm{H}_{2} \mathrm{PO}_{4}^{-}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\left[\mathrm{H}_{3} \mathrm{PO}_{4}\right]}=7.11 \times 10^{-3} \nonumber\]

\[\mathrm{H}_{2} \mathrm{PO}_{4}^-(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{HPO}_{4}^{2-}(a q) \nonumber\]

\[K_{a 2}=\frac{\left[\mathrm{HPO}_{4}^{2-}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\left[\mathrm{H}_{2} \mathrm{PO}_{4}^-\right]}=6.32 \times 10^{-8} \nonumber\]

\[\mathrm{HPO}_{4}^{2-}(a q)+\mathrm{H}_{2} \mathrm{O}({l})\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{PO}_{4}^{3-}(a q) \nonumber\]

\[K_{\mathrm{a} 3}=\frac{\left[\mathrm{PO}_{4}^{3-}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\left[\mathrm{HPO}_{4}^{2-}\right]}=4.5 \times 10^{-13} \nonumber\]

The decrease in the acid dissociation constants from K_a1 to K_a3 tells us that each successive proton is harder to remove. Consequently, H₃PO₄ is a stronger acid than \(\text{H}_2\text{PO}_4^-\), and \(\text{H}_2\text{PO}_4^-\) is a stronger acid than \(\text{HPO}_4^{2-}\).

Strong and Weak Bases

The most common example of a strong base is an alkali metal hydroxide, such as sodium hydroxide, NaOH, which completely dissociates to produce hydroxide ion.

\[\mathrm{NaOH}(s) \rightarrow \mathrm{Na}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber\]

A weak base, such as the acetate ion, CH₃COO^–, only partially accepts a proton from the solvent, and is characterized by a base dissociation constant, K_b. For example, the base dissociation reaction and the base dissociation constant for the acetate ion are

\[\mathrm{CH}_{3} \mathrm{COO}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{CH}_{3} \mathrm{COOH}(a q) \nonumber\]

\[K_{\mathrm{b}}=\frac{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]}=5.71 \times 10^{-10} \nonumber\]

A polyprotic weak base, like a polyprotic acid, has more than one base dissociation reaction and more than one base dissociation constant.

Amphiprotic Species

Some species can behave as either a weak acid or as a weak base. For example, the following two reactions show the chemical reactivity of the bicarbonate ion, \(\text{HCO}_3^-\), in water.

\[\mathrm{HCO}_{3}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{CO}_{3}^{2-}(a q) \label{6.3}\]

\[\mathrm{HCO}_{3}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{H}_{2} \mathrm{CO}_{3}(a q) \label{6.4}\]

A species that is both a proton donor and a proton acceptor is called amphiprotic. Whether an amphiprotic species behaves as an acid or as a base depends on the equilibrium constants for the competing reactions. For bicarbonate, the acid dissociation constant for reaction \ref{6.3}

\[K_{a 2}=\frac{\left[\mathrm{CO}_{3}^{2-}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\left[\mathrm{HCO}_{3}^{-}\right]}=4.69 \times 10^{-11} \nonumber\]

is smaller than the base dissociation constant for reaction \ref{6.4}.

\[K_{\mathrm{b} 2}=\frac{\left[\mathrm{H}_{2} \mathrm{CO}_{3}\right]\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{HCO}_{3}^{-}\right]}=2.25 \times 10^{-8} \nonumber\]

Because bicarbonate is a stronger base than it is an acid, we expect that an aqueous solution of \(\text{HCO}_3^-\) is basic.

Dissociation of Water

Water is an amphiprotic solvent because it can serve as an acid or as a base. An interesting feature of an amphiprotic solvent is that it is capable of reacting with itself in an acid–base reaction.

\[2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \label{6.5}\]

We identify the equilibrium constant for this reaction as water’s dissociation constant, K_w,

\[K_{w}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=1.00 \times 10^{-14} \label{6.6}\]

at a temperature of 24^oC. The value of K_w varies substantially with temperature. For example, at 20^oC K_w is \(6.809 \times 10^{-15}\), while at 30^oC K_w is \(1.469 \times 10^{-14}\). At 25^oC, K_w is \(1.008 \times 10^{-14}\), which is sufficiently close to \(1.00 \times 10^{-14}\) that we can use the latter value with negligible error.

An important consequence of Equation \ref{6.6} is that the concentration of H₃O⁺ and the concentration of OH^– are related. If we know [H₃O⁺] for a solution, then we can calculate [OH^–] using Equation \ref{6.6}.

Example 6.4.1

What is the [OH^–] if the [H₃O⁺] is \(6.12 \times 10^{-5}\) M?

Solution

\[\left[\mathrm{OH}^{-}\right]=\frac{K_{w}}{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}=\frac{1.00 \times 10^{-14}}{6.12 \times 10^{-5}}=1.63 \times 10^{-10} \nonumber\]

The pH Scale

Equation \ref{6.6} allows us to develop a pH scale (\(\text{pH} = - \log [\text{H}_3\text{O}^+]\)) that indicates a solution’s acidity. When the concentrations of H₃O⁺ and OH^– are equal a solution is neither acidic nor basic; that is, the solution is neutral. Letting

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{-}\right] \nonumber\]

substituting into Equation \ref{6.6}

\[K_{w}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{2}=1.00 \times 10^{-14} \nonumber\]

and solving for [H₃O⁺] gives

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\sqrt{1.00 \times 10^{-14}}=1.00 \times 10^{-7} \nonumber\]

A neutral solution of water at 25^oC has a hydronium ion concentration of \(1.00 \times 10^{-7}\) M and a pH of 7.00. In an acidic solution the concentration of H₃O⁺ is greater than that for OH^–, which means that

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]>1.00 \times 10^{-7} \mathrm{M} \nonumber\]

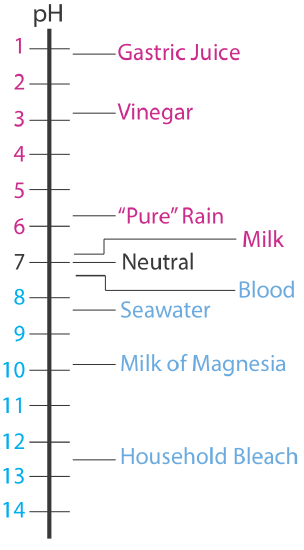
The pH of an acidic solution, therefore, is less than 7.00. A basic solution, on the other hand, has a pH greater than 7.00. Figure 6.4.1 shows the pH scale and pH values for some representative solutions.

Figure 6.4.1 . Scale showing the pH value for representative solutions. Milk of Magnesia is a saturated solution of Mg(OH)₂.

Tabulating Values for K_a and K_b

A useful observation about weak acids and weak bases is that the strength of a weak base is inversely proportional to the strength of its conjugate weak acid. Consider, for example, the dissociation reactions of acetic acid and acetate.

\[\mathrm{CH}_{3} \mathrm{COOH}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \ \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{CH}_{3} \mathrm{COO}^{-}(a q) \label{6.7}\]

\[\mathrm{CH}_{3} \mathrm{COO}^{-}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{OH}^{-}(a q)+\mathrm{CH}_{3} \mathrm{COOH}(a q) \label{6.8}\]

Adding together these two reactions gives the reaction

\[2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q) \nonumber\]

for which the equilibrium constant is K_w. Because adding together two reactions is equivalent to multiplying their respective equilibrium constants, we may express K_w as the product of K_a for CH3COOH and K_b for CH3COO^–.

\[K_{\mathrm{w}}=K_{\mathrm{a}, \mathrm{CH}_{3} \mathrm{COOH}} \times K_{\mathrm{b}, \mathrm{CH}_{3} \mathrm{COO}^{-}} \nonumber\]

For any weak acid, HA, and its conjugate weak base, A^–, we can generalize this to the following equation

\[K_{\mathrm{w}}=K_{\mathrm{a}, \mathrm{HA}} \times K_{\mathrm{b}, \mathrm{A}^{-}} \label{6.9}\]

where HA and A^– are a conjugate acid–base pair. The relationship between K_a and K_b for a conjugate acid–base pair simplifies our tabulation of acid and base dissociation constants. Appendix 11 includes acid dissociation constants for a variety of weak acids. To find the value of K_b for a weak base, use Equation \ref{6.9} and the K_a value for its corresponding weak acid.

A common mistake when using Equation \ref{6.9} is to forget that it applies to a conjugate acid–base pair only.

Example 6.4.2

Using Appendix 11, calculate values for the following equilibrium constants.

1. K_b for pyridine, C₅H₅N
2. K_b for dihydrogen phosphate, \(\text{H}_2\text{PO}_4^-\)

Solution

\[\text { (a) } K_{\mathrm{b}, \mathrm{C}_5 \mathrm{H}_{5} \mathrm{N}}=\frac{K_{\mathrm{w}}}{K_{\mathrm{a}, \mathrm{C}_{\mathrm{5}} \mathrm{H}_{5} \mathrm{NH}^{+}}}=\frac{1.00 \times 10^{-14}}{5.90 \times 10^{-6}}=1.69 \times 10^{-9} \nonumber\]

\[\text { (b) } K_{\mathrm{b}, \mathrm{H}_2 \mathrm{PO}_{4}^- }=\frac{K_{\mathrm{w}}}{K_{\mathrm{a}, \mathrm{H}_{\mathrm{3}} \mathrm{PO}_{4} }}=\frac{1.00 \times 10^{-14}}{7.11 \times 10^{-3}}=1.41 \times 10^{-12} \nonumber\]

When finding the K_b value for a polyprotic weak base, be careful to choose the correct K_a value. Remember that Equation \ref{6.9} applies to a conjugate acid–base pair only. The conjugate acid of \(\text{H}_2\text{PO}_4^-\) is H₃PO₄, not \(\text{HPO}_4^{2-}\).

Exercise 6.4.1

Using Appendix 11, calculate K_b values for hydrogen oxalate, \(\text{HC}_2\text{O}_4^-\), and for oxalate, \(\text{C}_2\text{O}_4^{2-}\).

Answer

The K_b for hydrogen oxalate is

\[K_{\mathrm{b}, \mathrm{HC}_{2} \mathrm{O}_{4}^-}=\frac{K_{\mathrm{w}}}{K_{\mathrm{a}, \mathrm{H}_{2} \mathrm{C}_{2} \mathrm{O}_{4}}}=\frac{1.00 \times 10^{-14}}{5.60 \times 10^{-2}}=1.79 \times 10^{-13} \nonumber\]

and the K_b for oxalate is

\[K_{\mathrm{b}, \mathrm{C}_{2} \mathrm{O}_{4}^{2-}}=\frac{K_{\mathrm{w}}}{K_{\mathrm{a}, \mathrm{HC}_{2} \mathrm{O}_{\mathrm{4}}^-}}=\frac{1.00 \times 10^{-14}}{5.42 \times 10^{-5}}=1.85 \times 10^{-10} \nonumber\]

As we expect, the K_b value for \(\text{C}_2\text{O}_4^{2-}\) is larger than that for \(\text{HC}_2\text{O}_4^-\).

Complexation Reactions

A more general definition of acids and bases was proposed in 1923 by G. N. Lewis. The Brønsted‐Lowry definition of acids and bases focuses on an acid’s proton‐donating ability and a base’s proton‐accepting ability. Lewis theory, on the other hand, uses the breaking and the forming of covalent bonds to describe acids and bases. In this treatment, an acid is an electron pair acceptor and a base in an electron pair donor. Although we can apply Lewis theory to the treatment of acid–base reactions, it is more useful for treating complexation reactions between metal ions and ligands.

The following reaction between the metal ion Cd²⁺ and the ligand NH₃ is typical of a complexation reaction.

\[\mathrm{Cd}^{2+}(a q)+4: \mathrm{NH}_{3}(a q)\rightleftharpoons \mathrm{Cd}\left( : \mathrm{NH}_{3}\right)_{4}^{2+}(a q) \label{6.10}\]

The product of this reaction is a metal–ligand complex. In writing this reaction we show ammonia as :NH₃, using a pair of dots to emphasize the pair of electrons that it donates to Cd²⁺. In subsequent reactions we will omit this notation.

Metal-Ligand Formation Constants

We characterize the formation of a metal–ligand complex by a formation constant, K_f. For example, the complexation reaction between Cd²⁺ and NH₃, reaction \ref{6.10}, has the following equilibrium constant.

\[K_{f}=\frac{\left[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)_{4}^{2+}\right]}{\left[\mathrm{Cd}^{2+}\right]\left[\mathrm{NH}_{3}\right]^{4}}=5.5 \times 10^{7} \label{6.11}\]

The reverse of reaction \ref{6.10} is a dissociation reaction, which we characterize by a dissociation constant, K_d, that is the reciprocal of K_f.

Many complexation reactions occur in a stepwise fashion. For example, the reaction between Cd²⁺ and NH₃ involves four successive reactions.

\[\mathrm{Cd}^{2+}(a q)+\mathrm{NH}_{3}(a q) \rightleftharpoons \mathrm{Cd}\left(\mathrm{NH}_{3}\right)^{2+}(a q) \label{6.12}\]

\[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)^{2+}(a q)+\mathrm{NH}_{3}(a q)\rightleftharpoons \mathrm{Cd}\left(\mathrm{NH}_{3}\right)_{2}^{2+}(a q) \label{6.13}\]

\[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)_{2}^{2+}(a q)+\mathrm{NH}_{3}(a q)\rightleftharpoons \mathrm{Cd}\left(\mathrm{NH}_{3}\right)_{3}^{2+}(a q) \label{6.14}\]

\[\mathrm{Cd}\left(\mathrm{NH}_{3}\right)_{3}^{2+}(a q)+\mathrm{NH}_{3}(a q)\rightleftharpoons \mathrm{Cd}\left(\mathrm{NH}_{3}\right)_{4}^{2+}(a q) \label{6.15}\]

To avoid ambiguity, we divide formation constants into two categories. A stepwise formation constant, which we designate as K_i for the i^th step, describes the successive addition of one ligand to the metal–ligand complex from the previous step. Thus, the equilibrium constants for reactions \ref{6.12}–\ref{6.15} are, respectively, K₁, K₂, K₃, and K₄. An overall, or cumulative formation constant, which we designate as \(\beta_i\), describes the addition of i ligands to the free metal ion. The equilibrium constant in Equation \ref{6.11} is correctly identified as \(\beta_4\), where

\[\beta_{4}=K_{1} \times K_{2} \times K_{3} \times K_{4} \nonumber\]

In general

\[\beta_{n}=K_{1} \times K_{2} \times \cdots \times K_{n}=\prod_{i=1}^{n} K_{i} \nonumber\]

Stepwise and overall formation constants for selected metal–ligand complexes are in Appendix 12.

Metal-Ligand Complexation and Solubility

A formation constant describes the addition of one or more ligands to a free metal ion. To find the equilibrium constant for a complexation reaction that includes a solid, we combine appropriate K_sp and K_f expressions. For example, the solubility of AgCl increases in the presence of excess chloride ions as the result of the following complexation reaction.

\[\operatorname{AgCl}(s)+\mathrm{Cl}^{-}(a q)\rightleftharpoons\operatorname{Ag}(\mathrm{Cl})_{2}^{-}(a q) \label{6.16}\]

We can write this reaction as the sum of three other equilibrium reactions with known equilibrium constants—the solubility of AgCl, which is described by its K_sp reaction

\[\mathrm{AgCl}(s) \rightleftharpoons \mathrm{Ag}^{+}(a q)+\mathrm{Cl}^{-}(a q) \nonumber\]

and the stepwise formation of \(\text{AgCl}_2^-\), which is described by K₁and K ₂ reactions.

\[\mathrm{Ag}^{+}(a q)+\mathrm{Cl}^{-}(a q) \rightleftharpoons \operatorname{Ag} \mathrm{Cl}(a q) \nonumber\]

\[\operatorname{AgCl}(a q)+\mathrm{Cl}^{-}(a q) \rightleftharpoons \operatorname{AgCl}_{2}^{-}(a q) \nonumber\]

The equilibrium constant for reaction \ref{6.16}, therefore, is \(K_\text{sp} \times K_1 \times K_2\).

Example 6.4.3

Determine the value of the equilibrium constant for the reaction

\[\mathrm{PbCl}_{2}(s)\rightleftharpoons \mathrm{PbCl}_{2}(a q) \nonumber\]

Solution

We can write this reaction as the sum of three other reactions. The first of these reactions is the solubility of PbCl₂(s), which is described by its K_sp reaction.

\[\mathrm{PbCl}_{2}(s)\rightleftharpoons \mathrm{Pb}^{2+}(a q)+2 \mathrm{Cl}^{-}(a q) \nonumber\]

The remaining two reactions are the stepwise formation of PbCl₂(aq), which are described by K₁ and K₂.

\[\mathrm{Pb}^{2+}(a q)+\mathrm{Cl}^{-}(a q)\rightleftharpoons \mathrm{PbCl}^{+}(a q) \nonumber\]

\[\mathrm{PbCl}^{+}(a q)+\mathrm{Cl}^{-}(a q)\rightleftharpoons \mathrm{PbCl}_{2}(a q) \nonumber\]

Using values for K_sp, K₁, and K₂ from Appendix 10 and Appendix 12, we find that the equilibrium constant is

\[K=K_{\mathrm{sp}} \times K_{1} \times K_{2}=\left(1.7 \times 10^{-5}\right) \times 38.9 \times 1.62=1.1 \times 10^{-3} \nonumber\]

Exercise 6.4.2

What is the equilibrium constant for the following reaction? You will find appropriate equilibrium constants in Appendix 10 and Appendix 12.

\[\operatorname{Ag} \mathrm{Br}(s)+2 \mathrm{S}_{2} \mathrm{O}_{3}^{2-}(a q)\rightleftharpoons\operatorname{Ag}\left(\mathrm{S}_{2} \mathrm{O}_{3}\right)_2^{3-}(a q)+\mathrm{Br}^{-}(a q) \nonumber\]

Answer

We can write the reaction as a sum of three other reactions. The first reaction is the solubility of AgBr(s), which we characterize by its K_sp.

\[\operatorname{AgBr}(s)\rightleftharpoons\operatorname{Ag}^{+}(a q)+\mathrm{Br}^{-}(a q) \nonumber\]

The remaining two reactions are the stepwise formation of \(\text{Ag(S}_2\text{O}_3)_2^{3-}\), which we characterize by K₁ and K₂.

\[\mathrm{Ag}^{+}(a q)+\mathrm{S}_{2} \mathrm{O}_{3}^{2-}(a q)\rightleftharpoons\operatorname{Ag}\left(\mathrm{S}_{2} \mathrm{O}_{3}\right)^{-}(a q) \nonumber\]

\[\operatorname{Ag}\left(\mathrm{S}_{2} \mathrm{O}_{3}\right)^{-}(a q)+\mathrm{S}_{2} \mathrm{O}_{3}^{2-}(a q)\rightleftharpoons\operatorname{Ag}\left(\mathrm{S}_{2} \mathrm{O}_{3}\right)_{2}^{3-}(a q) \nonumber\]

Using values for K_sp, K₁, and K₂ from Appendix 10 and Appendix 12, we find that the equilibrium constant for our reaction is

\[K=K_{sp} \times K_{1} \times K_{2}=\left(5.0 \times 10^{-13}\right)\left(6.6 \times 10^{8}\right)\left(7.1 \times 10^{4}\right)=23 \nonumber\]

Oxidation–Reduction (Redox) Reactions

An oxidation–reduction reaction occurs when electrons move from one reactant to another reactant. As a result of this transfer of electrons, the reactants undergo a change in oxidation state. Those reactant that increases its oxidation state undergoes oxidation, and the reactant that decreases its oxidation state undergoes reduction. For example, in the following redox reaction between Fe³⁺ and oxalic acid, H₂C₂O₄, iron is reduced because its oxidation state changes from +3 to +2.

\[2 \mathrm{Fe}^{3+}(a q)+\mathrm{H}_{2} \mathrm{C}_{2} \mathrm{O}_{4}(a q)+2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \\ {2 \mathrm{Fe}^{2+}(a q)+2 \mathrm{CO}_{2}(g)+2 \mathrm{H}_{3} \mathrm{O}^{+}(a q)} \label{6.17}\]

Oxalic acid, on the other hand, is oxidized because the oxidation state for carbon increases from +3 in H₂C₂O₄ to +4 in CO₂.

We can divide a redox reaction, such as reaction \ref{6.17}, into separate half‐reactions that show the oxidation and the reduction processes.

\[\mathrm{H}_{2} \mathrm{C}_{2} \mathrm{O}_{4}(a q)+2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons 2 \mathrm{CO}_{2}(g)+2 \mathrm{H}_{3} \mathrm{O}^{+}(a q)+2 e^{-} \nonumber\]

\[\mathrm{Fe}^{3+}(a q)+e^{-} \rightleftharpoons \mathrm{Fe}^{2+}(a q) \nonumber\]

It is important to remember, however, that an oxidation reaction and a reduction reaction always occur as a pair. We formalize this relationship by identifying as a reducing agent the reactant that is oxidized, because it provides the electrons for the reduction half‐reaction. Conversely, the reactant that is reduced is an oxidizing agent. In reaction \ref{6.17}, Fe³⁺ is the oxidizing agent and H₂C₂O₄ is the reducing agent.

The products of a redox reaction also have redox properties. For example, the Fe²⁺ in reaction \ref{6.17} is oxidized to Fe³⁺ when CO₂ is reduced to H₂C₂O₄. Borrowing some terminology from acid–base chemistry, Fe²⁺ is the conjugate reducing agent of the oxidizing agent Fe³⁺, and CO₂ is the conjugate oxidizing agent of the reducing agent H₂C₂O₄.

Thermodynamics of Redox Reactions

Unlike precipitation reactions, acid–base reactions, and complexation reactions, we rarely express the equilibrium position of a redox reaction with an equilibrium constant. Because a redox reaction involves a transfer of electrons from a reducing agent to an oxidizing agent, it is convenient to consider the reaction’s thermodynamics in terms of the electron.

For a reaction in which one mole of a reactant undergoes oxidation or reduction, the net transfer of charge, Q, in coulombs is

\[Q=n F \nonumber\]

where n is the moles of electrons per mole of reactant, and F is Faraday’s constant (96485 C/mol). The free energy, ∆G, to move this charge, Q, over a change in potential, E, is

\[\triangle G=E Q \nonumber \]

The change in free energy (in kJ/mole) for a redox reaction, therefore, is

\[\Delta G=-n F E \label{6.18}\]

where ∆G has units of kJ/mol. The minus sign in Equation \ref{6.18} is the result of a different convention for assigning a reaction’s favorable direction. In thermodynamics, a reaction is favored when ∆G is negative, but an oxidation‐reduction reaction is favored when E is positive. Substituting Equation \ref{6.18} into equation 6.2.3

\[-n F E=-n F E^{\circ}+R T \ln Q_r \nonumber\]

and dividing by –nF, leads to the well‐known Nernst equation

\[E=E^{\circ}-\frac{R T}{n F} \ln Q_r \nonumber\]

where E^o is the potential under standard‐state conditions. Substituting appropriate values for R and F, assuming a temperature of 25 ^oC (298 K), and switching from ln to log gives the potential in volts as

\[E=E^{\mathrm{o}}-\frac{0.05916}{n} \log Q_r \label{6.19}\]

Standard Potentials

A redox reaction’s standard potential, E^o, provides an alternative way of expressing its equilibrium constant and, therefore, its equilibrium position. Because a reaction at equilibrium has a ∆G of zero, the potential, E, also is zero at equilibrium. Substituting these values into Equation \ref{6.19} and rearranging provides a relationship between E ^o and K

\[E^{\circ}=\frac{0.05916}{n} \log K \label{6.20}\]

A standard potential is the potential when all species are in their standard states. You may recall that we define standard state conditions as follows: all gases have unit partial pressures, all solutes have unit concentrations, and all solids and liquids are pure.

We generally do not tabulate standard potentials for redox reactions. Instead, we calculate E^o using the standard potentials for the corresponding oxidation half‐reaction and reduction half‐reaction. By convention, standard potentials are provided for reduction half‐reactions. The standard potential for a redox reaction, E^o, is

\[E^{\circ}=E_{red}^{\circ}-E_{ox}^{\circ} \nonumber\]

where \(E_{red}^{\circ}\) and \(E_{ox}^{\circ}\) are the standard reduction potentials for the reduction half‐reaction and the oxidation half‐reaction.

Because we cannot measure the potential for a single half‐reaction, we arbitrarily assign a standard reduction potential of zero to a reference half‐reaction

\[2 \mathrm{H}_{3} \mathrm{O}^{+}(a q)+2 e^{-}\rightleftharpoons 2 \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{H}_{2}(g) \nonumber\]

and report all other reduction potentials relative to this reference. Appendix 13 contains a list of selected standard reduction potentials. The more positive the standard reduction potential, the more favorable the reduction reaction is under standard state conditions. For example, under standard state conditions the reduction of Cu²⁺ to Cu (E^o = +0.3419 V) is more favorable than the reduction of Zn²⁺ to Zn (E^o = –0.7618 V).

Example 6.4.4

Calculate (a) the standard potential, (b) the equilibrium constant, and (c) the potential when [Ag⁺] = 0.020 M and [Cd²⁺] = 0.050 M, for the following reaction at 25^oC.

\[\mathrm{Cd}(s)+2 \mathrm{Ag}^{+}(a q)\rightleftharpoons2 \mathrm{Ag}(s)+\mathrm{Cd}^{2+}(a q) \nonumber\]

Solution

(a) In this reaction Cd is oxidized and Ag⁺ is reduced. The standard cell potential, therefore, is

\[E^{\circ} = E^{\circ}_{\text{Ag}^+/ \text{Ag}} - E^{\circ}_{\text{Cd}^{2+}/ \text{Cd}} = 0.7996 - (-0.4030) = 1.2026 \ \text{V} \nonumber\]

(b) To calculate the equilibrium constant we substitute appropriate values into Equation \ref{6.20}.

\[E^{\circ}=1.2026 \ \mathrm{V}=\frac{0.05916 \ \mathrm{V}}{2} \log K \nonumber\]

Solving for K gives the equilibrium constant as

\[\begin{array}{l}{\log K=40.6558} \\ {K=4.527 \times 10^{40}}\end{array} \nonumber\]

(c) To calculate the potential when [Ag⁺] is 0.020 M and [Cd²⁺] is 0.050M, we use the appropriate relationship for the reaction quotient, Q_r, in Equation \ref{6.19}.

\[\begin{array}{c}{E=E^{\circ}-\frac{0.05916 \ \mathrm{V}}{n} \log \frac{\left[\mathrm{Cd}^{2+}\right]}{\left[\mathrm{Ag}^{+}\right]^{2}}} \\ {E=1.2026 \ \mathrm{V}-\frac{0.05916 \ \mathrm{V}}{2} \log \frac{0.050}{(0.020)^{2}}=1.14 \ \mathrm{V}}\end{array} \nonumber\]

Exercise 6.4.3

For the following reaction at 25^oC

\[5 \mathrm{Fe}^{2+}(a q)+\mathrm{MnO}_{4}^{-}(a q)+8 \mathrm{H}^{+}(a q) \rightleftharpoons 5 \mathrm{Fe}^{3+}(a q)+\mathrm{Mn}^{2+}(a q)+4 \mathrm{H}_{2} \mathrm{O}(l) \nonumber\]

calculate (a) the standard potential, (b) the equilibrium constant, and (c) the potential under these conditions: [Fe²⁺] = 0.50 M, [Fe³⁺] = 0.10 M, [\(\text{MnO}_4^{-}\)] = 0.025 M, [Mn²⁺] = 0.015 M, and a pH of 7.00. See Appendix 13 for standard state reduction potentials.

Answer

The two half‐reactions are the oxidation of Fe²⁺ and the reduction of \(\text{MnO}_4^-\).

\[\mathrm{Fe}^{2+}(a q) \rightleftharpoons \mathrm{Fe}^{3+}(a q)+e^{-} \nonumber\]

\[\mathrm{MnO}_{4}^{-}(a q)+8 \mathrm{H}^{+}(a q)+5 e^{-} \rightleftharpoons \mathrm{Mn}^{2+}(a q)+4 \mathrm{H}_{2} \mathrm{O}(l) \nonumber\]

From Appendix 13, the standard state reduction potentials for these half‐reactions are

\[E_{\text{Fe}^{3+}/\text{Fe}^{2+}}^{\circ} = 0.771 \ \text{V and } E_{\text{MnO}_4^-/\text{Mn}^{2+}}^{\circ} = 1.51 \ \text{V} \nonumber\]

(a) The standard state potential for the reaction is

\[E^{\circ} = E_{\text{MnO}_4^-/\text{Mn}^{2+}}^{\circ} - E_{\text{Fe}^{3+}/\text{Fe}^{2+}}^{\circ} = 1.51 \ \text{V} - 0.771 \ \text{V } = 0.74 \ \text{V} \nonumber\]

(b) To calculate the equilibrium constant we substitute appropriate values into Equation \ref{6.20}.

\[E^{\circ}=0.74 \ \mathrm{V}=\frac{0.05916}{5} \log K \nonumber\]

Solving for K gives its value as \(3.5 \times 10^{62}\).

(c) To calculate the potential under these non‐standard state conditions, we make appropriate substitutions into the Nernst equation.

\[E=E^{\circ}-\frac{R T}{n F} \ln \frac{\left[\mathrm{Mn}^{2+}\right]\left[\mathrm{Fe}^{3+}\right]^{5}}{\left[\mathrm{MnO}_{4}^{-}\right]\left[\mathrm{Fe}^{2+}\right]^{5}\left[\mathrm{H}^{+}\right]^{8}} \nonumber\]

\[E=0.74-\frac{0.05916}{5} \log \frac{(0.015)(0.10)^{5}}{(0.025)(0.50)^{5}\left(1 \times 10^{-7}\right)^{8}}=0.12 \ \mathrm{V} \nonumber\]

When writing precipitation, acid–base, and metal–ligand complexation reactions, we represent acidity as H₃O⁺. Redox reactions more commonly are written using H⁺ instead of H₃O⁺. For the reaction in Exercise 6.4.3 , we could replace H⁺ with H₃O⁺ and increase the stoichiometric coefficient for H₂O from 4 to 12.