6.8: Buffer Solutions

Adding as little as 0.1 mL of concentrated HCl to a liter of H₂O shifts the pH from 7.0 to 3.0. Adding the same amount of HCl to a liter of a solution that 0.1 M in acetic acid and 0.1 M in sodium acetate, however, results in a negligible change in pH. Why do these two solutions respond so differently to the addition of HCl?

A mixture of acetic acid and sodium acetate is one example of an acid–base buffer. To understand how this buffer works to limit the change in pH, we need to consider its acid dissociation reaction

\[\mathrm{CH}_{3} \mathrm{COOH}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons\mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{CH}_{3} \mathrm{COO}^{-}(a q) \nonumber\]

and its corresponding acid dissociation constant

\[K_{a}=\frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]}=1.75 \times 10^{-5} \label{6.1}\]

Taking the negative log of the terms in Equation \ref{6.1} and solving for pH leaves us with the result shown here.

\[\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]} \nonumber\]

\[\mathrm{pH}=4.76+\log \frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]} \label{6.2}\]

You may recall that we developed these same equations in Chapter 6.6 when we introduced ladder diagrams.

Buffering occurs because of the logarithmic relationship between pH and the concentration ratio of acetate and acetic acid. Here is an example to illustrate this point. If the concentrations of acetic acid and acetate are equal, the buffer’s pH is 4.76. If we convert 10% of the acetate to acetic acid, by adding a strong acid, the ratio [CH₃COO^–]/[CH₃COOH] changes from 1.00 to 0.818, and the pH decreases from 4.76 to 4.67—a decrease of only 0.09 pH units.

The ratio [CH₃COO^–]/[CH₃COOH] becomes 0.9/1.1 = 0.818 and the pH becomes

\[\mathrm{pH}=4.76+\log (0.818)=4.67 \nonumber\]

Systematic Solution to Buffer Problems

Equation \ref{6.2} is written in terms of the equilibrium concentrations of CH₃COOH and of CH₃COO^–. A more useful relationship relates a buffer’s pH to the initial concentrations of the weak acid and the weak base. We can derive a general buffer equation by considering the following reactions for a weak acid, HA, and the soluble salt of its conjugate weak base, NaA.

\[\begin{array}{c}{\mathrm{NaA}(s) \rightarrow \mathrm{Na}^{+}(a q)+\mathrm{A}^{-}(a q)} \\ {\mathrm{HA}(a q)+\mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{A}^{-}(a q)} \\ {2 \mathrm{H}_{2} \mathrm{O}(l)\rightleftharpoons \mathrm{H}_{3} \mathrm{O}^{+}(a q)+\mathrm{OH}^{-}(a q)}\end{array} \nonumber\]

Because the concentrations of Na⁺, A^–, HA, H₃O⁺, and OH^– are unknown, we need five equations to define the solution’s composition. Two of these equations are the equilibrium constant expressions for HA and H₂O.

\[K_{a}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]} \label{6.3}\]

\[K_{w}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right] \nonumber\]

The remaining three equations are mass balance equations for HA and Na⁺

\[C_{\mathrm{HA}}+C_{\mathrm{NaA}}=[\mathrm{HA}]+\left[\mathrm{A}^{-}\right] \label{6.4}\]

\[C_{\mathrm{NaA}}=\left[\mathrm{Na}^{+}\right] \label{6.5}\]

and a charge balance equation

\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]+\left[\mathrm{Na}^{+}\right]=\left[\mathrm{OH}^{-}\right]+\left[\mathrm{A}^{-}\right] \label{6.6}\]

Substituting Equation \ref{6.5} into Equation \ref{6.6} and solving for [A^–] gives

\[\left[\mathrm{A}^{-}\right]=C_{\mathrm{NaA} }-\left[\mathrm{OH}^{-}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right] \label{6.7}\]

Next, we substitute Equation \ref{6.7} into Equation \ref{6.4}, which gives the concentration of HA as

\[[\mathrm{HA}]=C_{\mathrm{HA}}+\left[\mathrm{OH}^{-}\right]-\left[\mathrm{H}_{3} \mathrm{O}^{+}\right] \label{6.8}\]

Finally, we substitute Equation \ref{6.7} and Equation \ref{6.8} into Equation \ref{6.3} and solve for pH to arrive at a general equation for a buffer’s pH.

\[\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{C_{\mathrm{NaA} }-\left[\mathrm{OH}^{-}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}{C_{\mathrm{HA}}+\left[\mathrm{OH}^{-}\right]-\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]} \nonumber\]

If the initial concentrations of the weak acid, C_HA, and the weak base, C_NaA. are significantly greater than [H₃O⁺] and [OH^–], then we can simplify the general equation to the Henderson–Hasselbalch equation.

\[\mathrm{pH}=\mathrm{p} K_{\mathrm{a}}+\log \frac{C_{\mathrm{NaA}}}{C_{\mathrm{HA}}} \label{6.9}\]

As outlined below, the Henderson–Hasselbalch equation provides a simple way to calculate the pH of a buffer, and to determine the change in pH upon adding a strong acid or strong base.

Lawrence Henderson (1878‐1942) first developed a relationship between [H₃O⁺], [HA], and [A^–] while studying the buffering of blood. Kurt Hasselbalch (1874‐1962) modified Henderson’s equation by transforming it to the logarithmic form shown in Equation \ref{6.9}. The assumptions that lead to Equation \ref{6.9} result in a minimal error in pH (<±5%) for larger concentrations of HA and A^–, for concentrations of HA and A^– that are similar in magnitude, and for weak acid’s with pK_a values closer to 7. For most problems in this textbook, Equation \ref{6.9} provides acceptable results. Be sure, however, to test your assumptions. For a discussion of the Henderson–Hasselbalch equation, including the error inherent in Equation \ref{6.9}, see Po, H. N.; Senozan, N. M. “The Henderson–Hasselbalch Equation: Its History and Limitations,” J. Chem. Educ. 2001, 78, 1499–1503.

Example 6.8.1

Calculate the pH of a buffer that is 0.020 M in NH₃ and 0.030 M in NH₄Cl. What is the pH after we add 1.0 mL of 0.10 M NaOH to 0.10 L of this buffer?

Solution

The acid dissociation constant for \(\text{NH}_4^+\) is \(5.70 \times 10^{-10}\), which is a pK_a of 9.24. Substituting the initial concentrations of NH₃ and NH₄Cl into Equation \ref{6.9} and solving, we find that the buffer’s pH is

\[\mathrm{pH}=9.24+\log \frac{0.020}{0.030}=9.06 \nonumber\]

With a pH of 9.06, the concentration of H₃O⁺ is \(8.71 \times 10^{-10}\) and the concentration of OH^– is \(1.15 \times 10^{-5}\). Because both of these concentrations are much smaller than either \(C_{\text{NH}_3}\) or \(C_{\text{NH}_4\text{Cl}}\), the approximations used to derive Equation \ref{6.9} are reasonable.

Adding NaOH converts a portion of the \(\text{NH}_4^+\) to NH₃ following reaction

\[\mathrm{NH}_{4}^{+}(a q)+\mathrm{OH}^{-}(a q) \rightleftharpoons \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{NH}_{3}(a q) \nonumber\]

Because this reaction’s equilibrium constant is so large (it is equal to (K_b)^-1 or \(5.7 \times 10^4\)), we may treat the reaction as if it goes to completion. The new concentrations of \(\text{NH}_4^+\) and NH₃ are

\[C_{\mathrm{NH}_{4}^{+}}=\frac{\operatorname{mol} \ \mathrm{NH}_{4}^{+}- \ \mathrm{mol} \mathrm{OH}^{-}}{V_{\mathrm{total}}} \nonumber\]

\[C_{\mathrm{NH}_4^+}=\frac{(0.030 \ \mathrm{M})(0.10 \ \mathrm{L})-(0.10 \ \mathrm{M})\left(1.0 \times 10^{-3} \ \mathrm{L}\right)}{0.10 \ \mathrm{L}+1.0 \times 10^{-3} \ \mathrm{L}}=0.029 \ \mathrm{M} \nonumber\]

\[C_{\mathrm{NH}_{3}}=\frac{\mathrm{mol} \ \mathrm{NH}_{3}+\mathrm{mol} \ \mathrm{OH}^{-}}{V_{\mathrm{total}}} \nonumber\]

\[C_{\mathrm{NH}_3}=\frac{(0.020 \ \mathrm{M})(0.10 \ \mathrm{L})+(0.10 \ \mathrm{M})\left(1.0 \times 10^{-3} \ \mathrm{L}\right)}{0.10 \ \mathrm{L}+1.0 \times 10^{-3} \ \mathrm{L}}=0.021 \ \mathrm{M} \nonumber\]

Substituting these concentrations into the equation 6.60 gives a pH of

\[\mathrm{pH}=9.24+\log \frac{0.021}{0.029}=9.10 \nonumber\]

Note that adding NaOH increases the pH from 9.06 to 9.10. As we expect, adding a base makes the pH more basic. Checking to see that the pH changes in the right direction is one way to catch a calculation error.

Exercise 6.8.1

Calculate the pH of a buffer that is 0.10 M in KH₂PO₄ and 0.050 M in Na₂HPO₄. What is the pH after we add 5.0 mL of 0.20 M HCl to 0.10 L of this buffer. Use Appendix 11 to find the appropriate K_a value.

Answer

The acid dissociation constant for \(\text{H}_2\text{PO}_4^-\) is \(6.32 \times 10^{-8}\), or a pK_a of 7.199. Substituting the initial concentrations of \(\text{H}_2\text{PO}_4^-\) and \(\text{HPO}_4^{2-}\) into Equation \ref{6.9} and solving gives the buffer’s pH as

\[\mathrm{pH}=7.199+\log \frac{\left[\mathrm{HPO}_{4}^{2-}\right]}{\left[\mathrm{H}_{2} \mathrm{PO}_{4}^{-}\right]}=7.199+\log \frac{0.050}{0.10}=6.898 \approx 6.90\nonumber\]

Adding HCl converts a portion of \(\text{HPO}_4^{2-}\) to \(\text{H}_2\text{PO}_4^-\) as a result of the following reaction

\[\mathrm{HPO}_{4}^{2-}(a q)+\mathrm{H}_{3} \mathrm{O}^{+}(a q)\rightleftharpoons \mathrm{H}_{2} \mathrm{O}(l)+\mathrm{H}_{2} \mathrm{PO}_{4}^{-}(a q) \nonumber\]

Because this reaction’s equilibrium constant is so large (it is \(1.59 \times 10^7\)), we may treat the reaction as if it goes to completion. The new concentrations of \(\text{H}_2\text{PO}_4^-\) and \(\text{HPO}_4^{2-}\) are

\[C_{\mathrm{H}_{2} \mathrm{PO}_{4}^{4-}}=\frac{\mathrm{mol} \ \mathrm{H}_{2} \mathrm{PO}_{4}^{-}+\mathrm{mol} \ \mathrm{HCl}}{V_{\mathrm{total}}} \nonumber\]

\[C_{\mathrm{H}_{2} \mathrm{PO}_{4}^{4-}}=\frac{(0.10 \ \mathrm{M})(0.10 \ \mathrm{L})+(0.20 \ \mathrm{M})\left(5.0 \times 10^{-3} \ \mathrm{L}\right)}{0.10 \ \mathrm{L}+5.0 \times 10^{-3} \ \mathrm{L}}=0.105 \ \mathrm{M} \nonumber\]

\[C_{\mathrm{HPO}_{4}^{2-}}=\frac{\mathrm{mol} \ \mathrm{HPO}_{4}^{2-}-\mathrm{mol} \ \mathrm{HCl}}{V_{\mathrm{total}}} \nonumber\]

\[C_{\mathrm{HPO}_{4}^{2-}}=\frac{(0.05 \ \mathrm{M})(0.10 \ \mathrm{L})-(0.20 \ \mathrm{M})\left(5.0 \times 10^{-3} \ \mathrm{L}\right)}{0.10 \ \mathrm{L}+5.0 \times 10^{-3} \ \mathrm{L}}=0.0381 \ \mathrm{M} \nonumber\]

Substituting these concentrations into Equation \ref{6.9} gives a pH of

\[\mathrm{pH}=7.199+\log \frac{\left[\mathrm{HPO}_{4}^{2-}\right]}{\left[\mathrm{H}_{2} \mathrm{PO}_{4}^-\right]}=7.199+\log \frac{0.0381}{0.105}=6.759 \approx 6.76 \nonumber\]

As we expect, adding HCl decreases the buffer’s pH by a small amount, dropping from 6.90 to 6.76.

We can use a multiprotic weak acid to prepare buffers at as many different pH’s as there are acidic protons, with the Henderson–Hasselbalch equation applying in each case. For example, for malonic acid (pK_a1 = 2.85 and pK_a2 = 5.70) we can prepare buffers with pH values of

\[\begin{array}{l}{\mathrm{pH}=2.85+\log \frac{C_{\mathrm{HM}^{-}}}{C_{\mathrm{H}_{2} \mathrm{M}}}} \\ {\mathrm{pH}=5.70+\log \frac{C_{\mathrm{M}^{2-}}}{C_{\mathrm{HM}^-}}}\end{array} \nonumber\]

where H₂M, HM^– and M^2– are malonic acid’s different acid–base forms.

Although our treatment of buffers is based on acid–base chemistry, we can extend buffers to equilibria that involve complexation or redox reactions. For example, the Nernst equation for a solution that contains Fe²⁺ and Fe³⁺ is similar in form to the Henderson‐Hasselbalch equation.

\[E=E_{\mathrm{Fe}^{3+} / \mathrm{Fe}^{2+}}^{\circ}-0.05916 \log \frac{\left[\mathrm{Fe}^{2+}\right]}{\left[\mathrm{Fe}^{3+}\right]} \nonumber\]

A solution that contains similar concentrations of Fe²⁺ and Fe³⁺ is buffered to a potential near the standard state reduction potential for Fe³⁺. We call such solutions redox buffers. Adding a strong oxidizing agent or a strong reducing agent to a redox buffer results in a small change in potential.

Representing Buffer Solutions with Ladder Diagrams

A ladder diagram provides a simple way to visualize a solution’s predominate species as a function of solution conditions. It also provides a convenient way to show the range of solution conditions over which a buffer is effective. For example, an acid–base buffer exists when the concentrations of the weak acid and its conjugate weak base are similar. For convenience, let’s assume that an acid–base buffer exists when

\[\frac{1}{10} \leq \frac{\left[\mathrm{CH}_{3} \mathrm{COO}^{-}\right]}{\left[\mathrm{CH}_{3} \mathrm{COOH}\right]} \leq \frac{10}{1} \nonumber\]

Substituting these ratios into the Henderson–Hasselbalch equation

\[\begin{aligned} \mathrm{pH} &=\mathrm{p} K_{\mathrm{a}}+\log \frac{1}{10}=\mathrm{p} K_{\mathrm{a}}-1 \\ \mathrm{pH} &=\mathrm{p} K_{\mathrm{a}}+\log \frac{10}{1}=\mathrm{p} K_{\mathrm{a}}+1 \end{aligned} \nonumber\]

shows that an acid–base buffer works over a pH range of pK_a ± 1.

Using the same approach, it is easy to show that a metal‐ligand complexation buffer for ML_n exists when

\[\mathrm{pL}=\log K_{n} \pm 1 \text { or } \mathrm{pL}=\log \beta_{n} \pm \frac{1}{n} \nonumber\]

where K_n or \(\beta_n\) is the relevant stepwise or overall formation constant. For an oxidizing agent and its conjugate reducing agent, a redox buffer exists when

\[E=E^{\circ} \pm \frac{1}{n} \times \frac{R T}{F}=E^{\circ} \pm \frac{0.05916}{n}\left(\text { at } 25^{\circ} \mathrm{C}\right) \nonumber\]

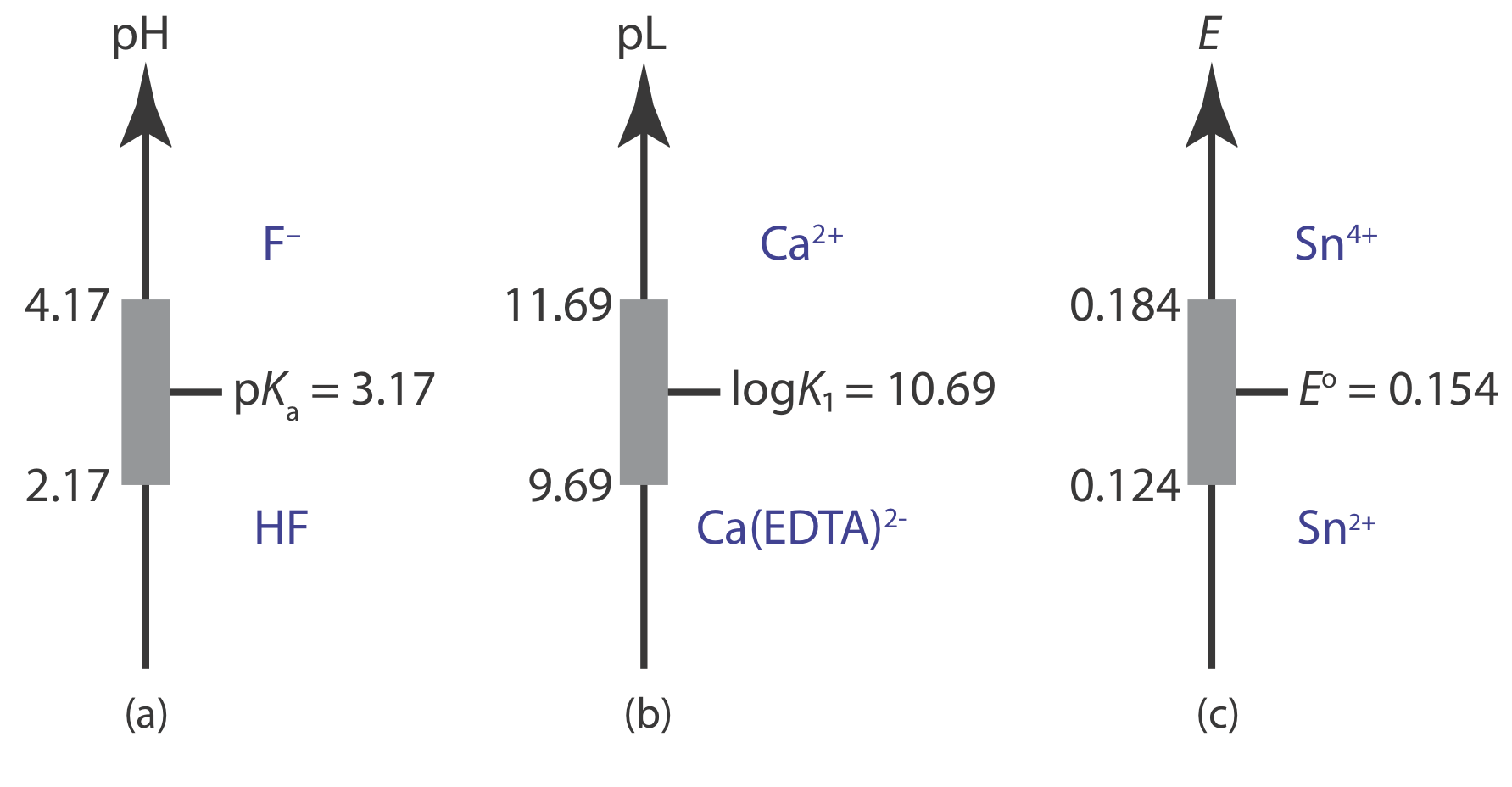
Figure 6.8.1 shows ladder diagrams with buffer regions for several equilibrium systems.

Figure 6.8.1 . Ladder diagrams showing buffer regions shaded in grey for (a) an acid–base buffer of HF and F^–; (b) a metal–ligand complexation buffer of Ca²⁺ and Ca(EDTA)^2–; and (c) an oxidation–reduction (redox) buffer of Sn⁴⁺ and Sn²⁺.

Preparing a Buffer

Buffer capacity is the ability of a buffer to resist a change in pH when we add to it a strong acid or a strong base. A buffer’s capacity to resist a change in pH is a function of the concentrations of the weak acid and the weak base, as well as their relative proportions. The importance of the weak acid’s concentration and the weak base’s concentration is obvious. The more moles of weak acid and weak base a buffer has, the more strong base or strong acid it can neutralize without a significant change in its pH.

Although a higher concentration of buffering agents provides greater buffer capacity, there are reasons for using smaller concentrations, including the formation of unwanted precipitates and the tolerance of biological systems for high concentrations of dissolved salts.

The relative proportions of a weak acid and a weak base also affects how much the pH changes when we add a strong acid or a strong base. A buffer that is equimolar in weak acid and weak base requires a greater amount of strong acid or strong base to bring about a one unit change in pH. Consequently, a buffer is most effective against the addition of strong acids or strong bases when its pH is near the weak acid’s pK_a value.

Buffer solutions are often prepared using standard “recipes” found in the chemical literature [see, for example, (a) Bower, V. E.; Bates, R. G. J. Res. Natl. Bur. Stand. (U. S.) 1955, 55, 197– 200; (b) Bates, R. G. Ann. N. Y. Acad. Sci. 1961, 92, 341–356; (c) Bates, R. G. Determination of pH, 2nd ed.; Wiley‐Interscience: New York, 1973]. In addition, there are computer programs and on‐line calculators to aid in preparing buffers [(a) Lambert, W. J. J. Chem. Educ. 1990, 67, 150–153; (b) http://www.bioinformatics.org/JaMBW/5/4/index.html.]. Perhaps the simplest way to make a buffer, however, is to prepare a solution that contains an appropriate conjugate weak acid and weak base, measure its pH, and then adjust the pH to the desired value by adding small portions of either a strong acid or a strong base.

A good “rule of thumb” when choosing a buffer is to select one whose reagents have a pK_a value close to your desired pH.