6.9: Activity Effects

Careful measurements on the metal–ligand complex Fe(SCN)²⁺ suggest its stability decreases in the presence of inert ions [Lister, M. W.; Rivington, D. E. Can. J. Chem. 1995, 33, 1572–1590]. We can demonstrate this by adding an inert salt to an equilibrium mixture of Fe³⁺ and SCN^–. Figure 6.9.1 a shows the result of mixing together equal volumes of 1.0 mM FeCl₃ and 1.5 mM KSCN, both of which are colorless. The solution’s reddish–orange color is due to the formation of Fe(SCN)²⁺.

\[\mathrm{Fe}^{3+}(a q)+\mathrm{SCN}^{-}(a q) \rightleftharpoons \mathrm{Fe}(\mathrm{SCN})^{2+}(a q) \label{6.1}\]

Figure 6.9.1 . The effect of a inert salt on a reaction’s equilibrium position is shown by the solutions in these two beakers. The beaker on the left contains equal volumes of 1.0 mM FeCl₃ and 1.5 mM KSCN. The solution’s color is due to the formation of the metal–ligand complex Fe(SCN)²⁺. Adding 10 g of KNO₃ to the beaker on the left produces the result shown on the right. The lighter color suggests that there is less Fe(SCN)²⁺ as a result of the equilibrium in reaction \ref{6.1} shifting to the left.

Adding 10 g of KNO₃ to the solution and stirring to dissolve the solid, produces the result shown in Figure 6.9.1 b. The solution’s lighter color suggests that adding KNO₃ shifts reaction \ref{6.1} to the left, decreasing the concentration of Fe(SCN)²⁺ and increasing the concentrations of Fe³⁺ and SCN^–. The result is a decrease in the complex’s formation constant, K₁.

\[K_{1}=\frac{\left[\mathrm{Fe}(\mathrm{SCN})^{2+}\right]}{\left[\mathrm{Fe}^{3+}\right]\left[\mathrm{SCN}^{-}\right]} \label{6.2}\]

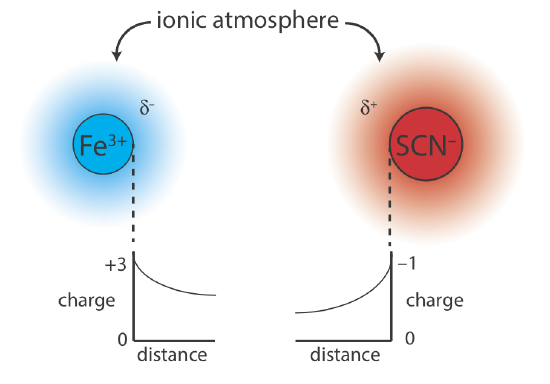
Why should adding an inert electrolyte affect a reaction’s equilibrium position? We can explain the effect of KNO₃ on the formation of Fe(SCN)²⁺ if we consider the reaction on a microscopic scale. The solution in Figure 6.9.1 b contains a variety of cations and anions: Fe³⁺, SCN^–, K⁺, \(\text{NO}_3^-\), H₃O⁺, and OH^–. Although the solution is homogeneous, on average, there are slightly more anions in regions near the Fe³⁺ ions, and slightly more cations in regions near the SCN^– ions. As shown in Figure 6.9.2 , each Fe³⁺ ion and each SCN^– ion is surrounded by an ionic atmosphere of opposite charge (\(\delta^–\) and \(\delta^+\)) that partially screen the ions from each other. Because each ion’s apparent charge at the edge of its ionic atmosphere is less than its actual charge, the force of attraction between the two ions is smaller. As a result, the formation of Fe(SCN)²⁺ is slightly less favorable and the formation constant in Equation \ref{6.2} is slightly smaller. Higher concentrations of KNO₃ increase \(\delta^–\) and \(\delta^+\), resulting in even smaller values for the formation constant.

Figure 6.9.2 . Ions of Fe³⁺ and SCN^– are surrounded by ionic atmospheres with net charges of \(\delta^–\) and \(\delta^+\). Because of these ionic atmospheres, each ion’s apparent charge at the edge of its ionic atmosphere is less than the ion’s actual charge.

Ionic Strength

To factor the concentration of ions into the formation constant for Fe(SCN)²⁺, we need a way to express that concentration in a meaningful way. Because both an ion’s concentration and its charge are important, we define the solution’s ionic strength, \(\mu\) as

\[\mu=\frac{1}{2} \sum_{i=1}^{n} c_{i} z_{i}^{2} \nonumber\]

where c_i and z_i are the concentration and charge of the i^th ion.

Example 6.9.1

Calculate the ionic strength of a solution of 0.10 M NaCl. Repeat the calculation for a solution of 0.10 M Na₂SO₄.

Solution

The ionic strength for 0.10 M NaCl is

\[\begin{array}{c}{\mu=\frac{1}{2}\left\{\left[\mathrm{Na}^{+}\right] \times(+1)^{2}+\left[\mathrm{Cl}^{-}\right] \times(-1)^{2}\right\}} \\ {\mu=\frac{1}{2}\left\{(0.10) \times(+1)^{2}+(0.10) \times(-1)^{2}\right\}=0.10 \ \mathrm{M}}\end{array} \nonumber\]

For 0.10 M Na₂SO₄ the ionic strength is

\[\begin{array}{c}{\mu=\frac{1}{2}\left\{\left[\mathrm{Na}^{+}\right] \times(+1)^{2}+\left[\mathrm{SO}_{4}^{2-}\right] \times(-2)^{2}\right\}} \\ {\mu=\frac{1}{2}\left\{(0.20) \times(+1)^{2}+(0.10) \times(-2)^{2}\right\}=0.30 \ \mathrm{M}}\end{array} \nonumber\]

In calculating the ionic strengths of these solutions we are ignoring the presence of H₃O⁺ and OH^–, and, in the case of Na₂SO₄, the presence of \(\text{HSO}_4^-\) from the base dissociation reaction of \(\text{SO}_4^{2-}\). In the case of 0.10 M NaCl, the concentrations of H₃O⁺ and OH^– are \(1.0 \times 10^{-7}\), which is significantly smaller than the concentrations of Na⁺ and Cl^–. Because \(\text{SO}_4^{2-}\) is a very weak base (K_b = \(1.0 \times 10^{-12}\)), the solution is only slightly basic (pH = 7.5), and the concentrations of H₃O⁺, OH^–, and \(\text{HSO}_4^-\) are negligible. Although we can ignore the presence of H₃O⁺, OH^–, and \(\text{HSO}_4^-\) when we calculate the ionic strength of these two solutions, be aware that an equilibrium reaction can generate ions that might affect the solution’s ionic strength.

Note that the unit for ionic strength is molarity, but that a salt’s ionic strength need not match its molar concentration. For a 1:1 salt, such as NaCl, ionic strength and molar concentration are identical. The ionic strength of a 2:1 electrolyte, such as Na₂SO₄, is three times larger than the electrolyte’s molar concentration.

Activity and Activity Coefficients

Figure 6.9.1 shows that adding KNO₃ to a mixture of Fe³⁺ and SCN^– decreases the formation constant for Fe(SCN)²⁺. This creates a contradiction. Earlier in this chapter we showed that there is a relationship between a reaction’s standard‐state free energy, ∆G^o, and its equilibrium constant, K.

\[\triangle G^{\circ}=-R T \ln K \nonumber\]

Because a reaction has only one standard‐state, its equilibrium constant must be independent of solution conditions. Although ionic strength affects the apparent formation constant for Fe(SCN)²⁺, reaction \ref{6.1} must have an underlying thermodynamic formation constant that is independent of ionic strength.

The apparent formation constant for Fe(SCN)²⁺, as shown in Equation \ref{6.2}, is a function of concentrations. In place of concentrations, we define the true thermodynamic equilibrium constant using activities. The activity of species A, a_A, is the product of its concentration, [A], and a solution‐dependent activity coefficient, \(\gamma_A\)

\[a_{A}=[A] \gamma_{A} \nonumber\]

The true thermodynamic formation constant for Fe(SCN)²⁺, therefore, is

\[K_{1}=\frac{a_{\mathrm{Fe}(S \mathrm{CN})^{2+}}}{a_{\mathrm{Fe}^{3+}} \times a_{\mathrm{SCN}^-}}=\frac{\left[\mathrm{Fe}(\mathrm{SCN})^{2+}\right] \gamma_{\mathrm{Fe}(\mathrm{SCN})^{2+}}}{\left[\mathrm{Fe}^{3+}\right] \gamma_{\mathrm{Fe}^{3+}}\left[\mathrm{SCN}^{-}\right] \gamma_{\mathrm{SCN}^{-}}} \nonumber\]

Unless otherwise specified, the equilibrium constants in the appendices are thermodynamic equilibrium constants.

A species’ activity coefficient corrects for any deviation between its physical concentration and its ideal value. For a gas, a pure solid, a pure liquid, or a non‐ionic solute, the activity coefficient is approximately one under most reasonable experimental conditions.

For a gas the proper terms are fugacity and fugacity coefficient, instead of activity and activity coefficient.

For a reaction that involves only these species, the difference between activity and concentration is negligible. The activity coefficient for an ion, however, depends on the solution’s ionic strength, the ion’s charge, and the ion’s size. It is possible to estimate activity coefficients using the extended Debye‐Hückel equation

\[\log \gamma_{A}=\frac{-0.51 \times z_{A}^{2} \times \sqrt{\mu}}{1+3.3 \times \alpha_{A} \times \sqrt{\mu}} \label{6.3}\]

where z_A is the ion’s charge, \(\alpha_A\) is the hydrated ion’s effective diameter in nanometers (Table 6.2), \(\mu\) is the solution’s ionic strength, and 0.51 and 3.3 are constants appropriate for an aqueous solution at 25^oC. A hydrated ion’s effective radius is the radius of the ion plus those water molecules closely bound to the ion. The effective radius is greater for smaller, more highly charged ions than it is for larger, less highly charged ions.

Table 6.9.1 . Effective Diameters (\(\alpha\)) for Selected Ions

ion	effective diameter (nm)
H3O^+	0.9
Li^+	0.6
Na^+, \(\text{IO}_3^-\), \(\text{HSO}_3^-\), \(\text{HCO}_3^-\), \(\text{H}_2\text{PO}_4^-\)	0.45
OH^–, F^–, SCN^–, HS^–, \(\text{ClO}_3^-\), \(\text{ClO}_4^-\), \(\text{MnO}_4^-\)	0.35
K^+, Cl^–, Br^–, I^–, CN^–, \(\text{NO}_2^-\), \(\text{NO}_3^-\)	0.3
Cs^+, Tl^+, Ag^+, \(\text{NH}_4^+\)	0.25
Mg^2^+, Be^2+	0.8
Ca^2^+, Cu^2+, Zn^2^+, Sn^2+, Mn^2^+, Fe^2+, Ni^2^+, Co^2+	0.6
Sr^2^+, Ba^2+, Cd^2+, Hg^2+, S^2–	0.5
Pb^2+, \(\text{SO}_4^{2-}\), \(\text{SO}_3^{2-}\)	0.45
\(\text{Hg}_2^{2+}\), \(\text{SO}_4^{2-}\), \(\text{S}_22\text{O}_3^{2-}\), \(\text{CrO}_4^{2-}\), \(\text{HPO}_4^{2-}\)	0.40
Al^3^+, Fe^3+, Cr^3^+	0.9
\(\text{PO}_4^{3-}\), \(\text{Fe(CN)}_6^{3-}\)	0.4
Zr^4^+, Ce^4+, Sn^4^+	1.1
\(\text{Fe(CN)}_6^{4-}\)	0.5
Source: Kielland, J. J. Am. Chem. Soc. 1937, 59, 1675–1678.

Several features of Equation \ref{6.3} deserve our attention. First, as the ionic strength approaches zero an ion’s activity coefficient approaches a value of one. In a solution where \(\mu = 0\), an ion’s activity and its concentration are identical. We can take advantage of this fact to determine a reaction’s thermodynamic equilibrium constant by measuring the apparent equilibrium constant for several increasingly smaller ionic strengths and extrapolating back to an ionic strength of zero. Second, an activity coefficient is smaller, and the effect of activity is more important, for an ion with a higher charge and a smaller effective radius. Finally, the extended Debye‐Hückel equation provides a reasonable estimate of an ion’s activity coefficient when the ionic strength is less than 0.1. Modifications to Equation \ref{6.3} extend the calculation of activity coefficients to higher ionic strengths [Davies, C. W. Ion Association, Butterworth: London, 1962].

Including Activity Coefficients When Solving Equilibrium Problems

Earlier in this chapter we calculated the solubility of Pb(IO₃)₂ in deionized water, obtaining a result of \(4.0 \times 10^{-5}\) mol/L. Because the only significant source of ions is from the solubility reaction, the ionic strength is very low and we can assume that \(\gamma \approx 1\) for both Pb²⁺ and \(\text{IO}_3^-\). In calculating the solubility of Pb(IO₃)₂ in deionized water, we do not need to account for ionic strength. But what if we need to know the solubility of Pb(IO₃)₂ in a solution that contains other, inert ions? In this case we need to include activity coefficients in our calculation.

Example 6.9.2

Calculate the solubility of Pb(IO₃)₂ in a matrix of 0.020 M Mg(NO₃)₂.

Solution

We begin by calculating the solution’s ionic strength. Since Pb(IO₃)₂ is only sparingly soluble, we will assume we can ignore its contribution to the ionic strength; thus

\[\mu=\frac{1}{2}\left\{(0.020)(+2)^{2}+(0.040)(-1)^{2}\right\}=0.060 \ \mathrm{M} \nonumber\]

Next, we use Equation \ref{6.3} to calculate the activity coefficients for Pb²⁺ and \(\text{IO}_3^-\).

\[\log \gamma_{\mathrm{Pb}^{2+}}=\frac{-0.51 \times(+2)^{2} \times \sqrt{0.060}}{1+3.3 \times 0.45 \times \sqrt{0.060}}=-0.366 \nonumber\]

\[\gamma_{\mathrm{Pb}^{2+}}=0.431 \nonumber\]

\[\log \gamma_{\mathrm{IO}_{3}^{-}}=\frac{-0.51 \times(-1)^{2} \times \sqrt{0.060}}{1+3.3 \times 0.45 \times \sqrt{0.060}}=-0.0916 \nonumber\]

\[\gamma_{\mathrm{IO}_{3}^-}=0.810 \nonumber\]

Defining the equilibrium concentrations of Pb²⁺ and \(\text{IO}_3^-\) in terms of the variable x

Concentrations	Pb(IO3)2 (s)	\(\rightleftharpoons\)	Pb^2^+ (aq)	+	2\(\text{IO}_3^-\) (aq)
initial	solid		0		0
change	solid		+x		+2x
equilibrium	solid		x		2x

and substituting into the thermodynamic solubility product for Pb(IO₃)₂ leaves us with

\[K_{\mathrm{sp}}=a_{\mathrm{Pb}^{2+}} \times a_{\mathrm{IO}_{3}^-}^{2}=\gamma_{\mathrm{Pb}^{2+}}\left[\mathrm{Pb}^{2+}\right] \times \gamma_{\mathrm{IO}_3^-}^{2}\left[\mathrm{IO}_{3}^{-}\right]^{2}=2.5 \times 10^{-13} \nonumber\]

\[K_{\mathrm{sp}}=(0.431)(x)(0.810)^{2}(2 x)^{2}=2.5 \times 10^{-13} \nonumber\]

\[K_{\mathrm{sp}}=1.131 x^{3}=2.5 \times 10^{-13} \nonumber\]

Solving for x gives \(6.0 \times 10^{-5}\) and a molar solubility of \(6.0 \times 10^{-5}\) mol/L for Pb(IO₃)₂. If we ignore activity, as we did in our earlier calculation, we report the molar solubility as \(4.0 \times 10^{-5}\) mol/L. Failing to account for activity in this case underestimates the molar solubility of Pb(IO₃)₂ by 33%.

The solution’s equilibrium composition is

\[\begin{array}{c}{\left[\mathrm{Pb}^{2+}\right]=6.0 \times 10^{-5} \ \mathrm{M}} \\ {\left[\mathrm{IO}_{3}^{-}\right]=1.2 \times 10^{-4} \ \mathrm{M}} \\ {\left[\mathrm{Mg}^{2+}\right]=0.020 \ \mathrm{M}} \\ {\left[\mathrm{NO}_{3}^{-}\right]=0.040 \ \mathrm{M}}\end{array} \nonumber\]

Because the concentrations of both Pb²⁺ and \(\text{IO}_3^-\) are much smaller than the concentrations of Mg²⁺ and \(\text{NO}_3^-\) our decision to ignore the contribution of Pb²⁺ and \(\text{IO}_3^-\) to the ionic strength is reasonable.

How do we handle the calculation if we can not ignore the concentrations of Pb²⁺ and \(\text{IO}_3^-\) when calculating the ionic strength. One approach is to use the method of successive approximations. First, we recalculate the ionic strength using the concentrations of all ions, including Pb²⁺ and \(\text{IO}_3^-\). Next, we recalculate the activity coefficients for Pb²⁺ and \(\text{IO}_3^-\) using this new ionic strength and then recalculate the molar solubility. We continue this cycle until two successive calculations yield the same molar solubility within an acceptable margin of error.

Exercise 6.9.1

Calculate the molar solubility of Hg₂Cl₂ in 0.10 M NaCl, taking into account the effect of ionic strength. Compare your answer to that from Exercise 6.7.2 in which you ignored the effect of ionic strength.

Answer

We begin by calculating the solution’s ionic strength. Because NaCl is a 1:1 ionic salt, the ionic strength is the same as the concentration of NaCl; thus \(\mu\) = 0.10 M. This assumes, of course, that we can ignore the contributions of \(\text{Hg}_2^{2+}\) and Cl^– from the solubility of Hg₂Cl₂.

Next we use Equation \ref{6.3} to calculate the activity coefficients for \(\text{Hg}_2^{2+}\) and Cl^–.

\[\log \gamma_{\mathrm{Hg}_{2}^{2+}}=\frac{-0.51 \times(+2)^{2} \times \sqrt{0.10}}{1+3.3 \times 0.40 \times \sqrt{0.10}}=-0.455 \nonumber\]

\[\gamma_{\mathrm{H} \mathrm{g}_{2}^{2+}}=0.351 \nonumber\]

\[\log \gamma_{\mathrm{Cl}^{-}}=\frac{-0.51 \times(-1)^{2} \times \sqrt{0.10}}{1+3.3 \times 0.3 \times \sqrt{0.10}}=-0.12 \nonumber\]

\[\gamma_{\mathrm{Cl}^-}=0.75 \nonumber\]

Defining the equilibrium concentrations of \(\text{Hg}_2^{2+}\) and Cl^– in terms of the variable x

concentrations	Hg2Cl2 (s)	\(\rightleftharpoons\)	\(\text{Hg}_2^{2+}\) (aq)	+	2Cl^– (aq)
initial	solid		0		0.10
change	solid		+x		+2x
equilibrium	solid		x		0.10 + 2x

and substituting into the thermodynamic solubility product for Hg₂Cl₂, leave us with

\[K_{\mathrm{sp}}=a_{\mathrm{Hg}_{2}^{2+}}\left(a_{\mathrm{Cl}^-}\right)^{2} = \gamma_{\mathrm{Hg}_{2}^{2+}}\left[\mathrm{Hg}_{2}^{2+}\right]\left(\gamma_{\mathrm{Cl}^{-}}\right)^{2}\left[\mathrm{Cl}^{-}\right]^{2}=1.2 \times 10^{-18} \nonumber\]

Because the value of x likely is small, let’s simplify this equation to

\[(0.351)(x)(0.75)^{2}(0.1)^{2}=1.2 \times 10^{-18} \nonumber\]

Solving for x gives its value as \(6.1 \times 10^{-16}\). Because x is the concentration of \(\text{Hg}_2^{2+}\) and 2x is the concentration of Cl^–, our decision to ignore their contributions to the ionic strength is reasonable. The molar solubility of Hg₂Cl₂ in 0.10 M NaCl is \(6.1 \times 10^{-16}\) mol/L. In Exercise 6.7.2, where we ignored ionic strength, we determined that the molar solubility of Hg₂Cl₂ is \(1.2 \times 10^{-16}\) mol/L, a result that is \(5 \times\) smaller than the its actual value.

As Example 6.9.2 and Exercise 6.9.1 show, failing to correct for the effect of ionic strength can lead to a significant error in an equilibrium calculation. Nevertheless, it is not unusual to ignore activities and to assume that the equilibrium constant is expressed in terms of concentrations. There is a practical reason for this—in an analysis we rarely know the exact composition, much less the ionic strength of aqueous samples or of solid samples brought into solution. Equilibrium calculations are a useful guide when we develop an analytical method; however, it only is when we complete an analysis and evaluate the results that can we judge whether our theory matches reality. In the end, work in the laboratory is the most critical step in developing a reliable analytical method.

This is a good place to revisit the meaning of pH. In Chapter 2 we defined pH as

\[\mathrm{pH}=-\log \left[\mathrm{H}_{3} \mathrm{O}^{+}\right] \nonumber\]

Now we see that the correct definition is

\[\begin{array}{c}{\mathrm{pH}=-\log a_{\mathrm{H}_{3} \mathrm{O}^{+}}} \\ {\mathrm{pH}=-\log \gamma_{\mathrm{H}_{3} \mathrm{O}^{+}}\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]}\end{array} \nonumber\]

Failing to account for the effect of ionic strength can lead to a significant error in the reported concentration of H₃O⁺. For example, if the pH of a solution is 7.00 and the activity coefficient for H₃O⁺ is 0.90, then the concentration of H₃O⁺ is \(1.11 \times 10^{-7}\) M, not \(1.00 \times 10^{-7}\) M, an error of +11%. Fortunately, when we develop and carry out an analytical method, we are more interested in controlling pH than in calculating [H₃O⁺]. As a result, the difference between the two definitions of pH rarely is of significant concern.