Extra Credit 47
- Page ID
- 83444
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Q 19.25B
Determine \(\Delta G^o\) for the following reactions:
a.\(O_2(g)+4H^+(aq)+4Br^−(aq)→2H_2O(l)+2Br_2(g)\)
b.\(Cr_2O_2^{−7}(aq)+14H^+(aq)+6K(s)→2Cr^{3+}(aq)+6K^+(aq)+7H_2O(l)\)
c.\(Cu(s)+Br_2(l)→Cu^{2+}(aq)+2Br^−(aq)\)
A 19.25B
For these sorts of questions, we will be using the Nernst equation. The Nernst equation (see below) is a way to convert Standard Electrode Potential to \(\Delta G^o\) using n, the moles of electrons, F, Faraday's constant, and \(E^o_{cell}\), which we obtain by finding the oxidation and reduction half reactions, looking at a table to find the corresponding Standard Reduction Potentials, and subtracting reduction-oxidation.
a. \(\Delta G^o = -nFE^o_{cell}\)
Write out oxidation and reduction half steps.
Oxidation: \(4Br^-(aq) \rightarrow 2Br_2(g)+4e^-\) Standard Reduction potential: +1.07
Reduction: \(O_2(g)+4H^+(aq) +4e^-\rightarrow 2H_2O(l)\) Standard Reduction Potential: +1.23
We now subtract the standard reduction potential (SRP) for the oxidation from the SRP for the reduction half reaction: 1.23-1.07=0.16
We can see that both half reactions have 4 electrons, so this is the moles of electrons transferred, n.
We now can plug this into our equation:
\(\Delta G^o=-4*(96,485)*.16=-61750.4\) J/mol
b. We repeat these steps as above.
Oxidation: \(6K(s)→6K^+(aq)+6e^−\) Standard Reduction Potential: -2.92
Reduction:\(Cr_2O_2^{−7}(aq)+6e^−+14H^+(aq)→2Cr^{3+}(aq)+7H_2O(l)\) Standard Reduction Potential: +1.33
Now we subtract: 1.33-(-2.92)=4.25
n=6
\(\Delta G^o = -6*(96485)*(4.25)=2460367.5\) J/mol or 2,460.368 kJ/mol
c. We repeat for the last equation:
Oxidation: \(Cu(s)→Cu^{2+}(aq)+2e^−\) Standard Reduction Potential: +0.34
Reduction: \(Br_2(l)+2e^−→2Br^−(aq)\) Standard Reduction Potential: +1.07
Both half reactions have 2 electrons, so it is balanced, and n=2.
SRP Reduction - SRP Oxidation: 0.73
\(\Delta G^o=-2*(96485)*(.73)=140868.1\) J/mol
Q20.5B
Show the possible Lewis structure for each ligands
- CO32-
- C2O42-
- NH3
A20.5B
The idea behind drawing a Lewis structure is to find the total number of valence electrons in the molecule based on the constituent atoms and the net charge, then to use the octet rule to fill the outer shells for every atom in the structure.
a. \(CO_3^{2-}\)
Carbon is in group 4A, so it has 4 valence electrons. Oxygen is in group 6A, so it has 6 valence electrons. We have three oxygen atoms in \(CO_3^{2-}\), so we have a further 6*3=18 valence electrons. Lastly, the net charge is 2-, so we add two more electrons. Our total number of electrons that we have to show in the structure is 4+18+2=24. Now, recall that single bonds represent 2 electrons of this total, double bonds represent 4 electrons, and triple bonds represent 6 electrons. Additionally, we can draw a lone pair if need be. Carbon, needing 8 valence electrons, will have 4 bonds. Each oxygen will have at least one bond. One oxygen will have a double bond to the central carbon atom. The remaining valence electrons for each oxygen will be accounted for by lone pairs to fill the octet. Thus we have:

We can count the valence electrons to be sure: 4 bonds=8 electrons. Then # of lone pairs= 8 = 16 electrons. 8+16=24 electrons, which is what we needed. Lastly, because there is a net charge, you must indicate this by placing a bracket around the Lewis structure and indicating the charge. Note that the double bond need not be on that particular oxygen atom; it could be oriented in any direction, and indeed may change. To indicate this, you should draw all three variations of the Lewis structure, or dotted lines to each oxygen to indicate the possibility of a double bond.
b. \(C_2O_4^{2-}\)
We shall proceed as before to find the Lewis structure. Carbon is in group 4A, so it has 4 valence electrons. We have two carbons, for a total of 8 electrons. Oxygen is in group 6A, so it contains 6 valence electrons. We have 4 oxygen atoms, for a total of 24 electrons. Finally, the net charge is 2-, so we will add 2 more electrons. Our total should be 8+24+2=34 valence electrons represented in the structure. There is no central carbon atom this time, as there are 2 carbon atoms, but because there are 2 carbons and 4 oxygens, we can draw the structure symmetrically, with the carbons bound to each other and two other oxygen atoms:
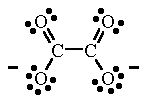
Again to check: each carbon atom has 4 bonds, for a full octet. Total number of bonds: 7=14 electrons. Number of lone pairs: 10= 20 electrons. So we have 14+20=34 total valence electrons shown, which is accurate. This image uses a different method of indicating net charge, as you may have noticed. Instead of brackets, it just places a - charge on each side of the atom- the meaning is the same. As before, the double bonds are not static; there is another resonance structure.
c. \(NH_3\)
Nitrogen is in group 5A, so it has 5 valence electrons. Hydrogen is in group 1A, so it has 1 valence electron. We have 3 hydrogen atoms for 3 valence electrons. There is a net charge of 0 on this molecule, so our total number of valence electrons remains 5+3=8. Nitrogen will be the central atom. Now, hydrogen is a special atom. It does not follow the octet rule. Rather, it only has 2 valence electrons in its shell. Typically, this will be filled by a single bond to another atom. So we will have all 3 hydrogen atoms bonded to the central nitrogen atom, with 2 electrons unaccounted for, which we will use in the form of a lone pair to fill nitrogen's octet:

And if we count valence electrons, we get 3 bonds=6 electrons, 1 lone pair=2 electrons, 6+2=8 electrons total.
Q21.19A
When \(Fe^{2+}\) is linked to strong-field ligands in an octahedral complex, it has no unpaired electrons and is diamagnetic. However, when \(Fe^{2+}\) is bounded to a weak field ligand it has 4 unpaired electrons and is paramagnetic. What accounts for this difference?
A21.19A
Firstly, let us see how many d-electrons \(Fe^{2+}\) has: if we count in to the transition metals, we see that it is the 6th. It therefore has 6 d-electrons, with 2 \(4s^1\) electrons. However, the 2+ charge means that the \(4s^1\) electrons will be removed, leaving the 6 d-electrons. So \(Fe^{2+}\) has 6 d-electrons.
Strong-field ligands induce a greater \(\Delta_o\), or crystal field splitting energy for octahedral complexes. Recall that electrons are paired when \(\Delta_o>P\), where P is spin-pairing energy. In this case, strong-field ligands cause the electrons to pair up in the lower orbitals, as it takes less energy to pair up than for the electrons to jump to a higher energy level. Therefore, all 6 electrons fill the 3 lower \(t_2g\) orbitals first, leaving none unpaired.
The weak-field ligand causes \(\Delta_o\) to be less than P, so it takes less energy to jump to a higher energy level than to pair up. Therefore, all 5 orbitals will be filled before the last electron pairs up with one in the \(t_2g\) orbitals, leaving 4 unpaired.
Q24.27A
Using Table A, determine whether each set is zero-order, first-order, or third-order.
|
I |
II |
III |
|||
|---|---|---|---|---|---|
|
Time, s |
[Reactant], M |
Time, s |
[Reactant], M |
Time, s |
[Reactant], M |
|
0 |
4.00 |
0 |
4.00 |
0 |
4.00 |
|
10 |
3.20 |
10 |
3.52 |
10 |
3.00 |
|
20 |
2.68 |
20 |
3.03 |
20 |
2.00 |
|
30 |
2.28 |
30 |
2.49 |
30 |
1.00 |
|
40 |
2.00 |
40 |
2.01 |
40 |
0.00 |
|
50 |
1.80 |
50 |
1.76 |
|
|
|
60 |
1.60 |
60 |
1.52 |
|
|
|
70 |
1.47 |
70 |
1.24 |
|
|
|
80 |
1.33 |
80 |
0.99 |
|
|
A24.27A
This question is dealing with the kinetics of reactions. Let's think about the defining characteristics for each order of reaction:
Zero order reaction: \([A]=[A]_o-kt\) Meaning concentration decreases linearly with time.
First order reaction: \(ln[A]=ln[A]_o-kt\) Meaning the natural log of concentration decreases linearly with time.
Second order reaction: \(1/[A]=1/[A]_o +kt\) Meaning 1/concentration increases linearly with time.
I. Let us look at the column for [reaction] and see how it is changing with time. It is not a zero order reaction because we do not see right away that the reactant concentration is decreasing consistently. Now let's take this to Excel and plug in some values, looking at the graphs we make. We will make a graph for ln[A] vs. time and 1/[A] vs. time:
From these graphs, which were made by plugging in the values to a spreadsheet and then creating the formula columns (=LN() and =1/()), we produced these graphs. It is now easy to tell that this, phase I, is a 2nd order reaction, as it increases linearly with time. You could achieve the same effect by calculating ln[A] for the first few values, seeing if they decreased linearly. Then calculate 1/[A], again seeing if it increases linearly.
II. Again, we do not see that the concentration values are decreasing linearly with time, so we shall again go to the spreadsheet (or calculator):
This one is slightly more difficult to interpret, but 1/[A] is clearly sloping upward; ln[A] has on average a linear negative slope. Therefore, it will be a first order reaction.
III. We can glance at this last column and see that every ten seconds, the reactant concentration decreases by 1 M. Therefore, this is linearly decreasing with respect to time, and it is a 0 order reaction.
Q25.10C
Complete the following nuclear equations
- \(^{24}_{12}Mg+? \rightarrow ^{25}_{11}Na+^1_1H\)
- \(^{60}_{28}Ni+^1_0n \rightarrow ^{57}_{26}Fe+?\)
- \(?+ ^2_1H \rightarrow ^{243}_{95}Am+^0_{-1}\beta\)
- \(^{247}_{97}Bk+? \rightarrow ^{254}_{102}No+5^1_0n\)
- \(^{239}_{93}Np+? \rightarrow ^{246}_{99}Es+6^1_0n\)
A25.10C
Remember that each of the above equations is set up in the form \(^A_ZX\), where A is the mass number (the sum of protons and neutrons in the nucleus), Z is the atomic number (number of protons/positive charges), and X is the element symbol. The goal for these types of problems is to balance the sums of A and Z on both sides of the equation by replacing the question mark with either an elementary particle of the right mass/charge, or an isotope of an element that will complete the equation.
a. Let's first find A on both sides of the equation: we take the sums of the A values for the reactants and products and set them equal to each other. Therefore, our equation becomes 24+?=25+1 or 24+?=26. The number that should go in this blank is 2.
Let's solve for Z, the number of protons/charge of the particle. Again, we sum up the two sides and solve with basic algebra for the unknown value. In this case, the equation is 12+?=11+1 or 12+?=12. The number that fills this blank is 0, implying that our particle has a charge of 0.
Now we must make up a mass number of 2 with a charge of 0. The only way to do this is to fill the blank with 2 neutrons, which each have a mass number of 1 and a charge of 0. So the equation becomes \(^{24}_{12}Mg+2^1_0n \rightarrow ^{25}_{11}Na+^1_1H\)
If you add the mass numbers and charges of the reactants and products, they should now be equal.
b. We use the same method for the rest of the parts:
Equation for mass number, A: 60+1 = 57+A
A=4
Equation for atomic number, Z: 28+0 = 26+Z
Z=2
Therefore, the missing particle has a mass number of 4 and an atomic number of 2. This is an alpha particle or helium nucleus, \(^4_2He\)
c. Equation for A: A+2 = 243+0
A=241
Equation for Z: Z+1 = 95+(-1)
Z=93
In this case, Z=93 is the atomic number, meaning we must look at a periodic table to determine what the element should be. Which element has an atomic number of 93? Neptunium, Np. Specifically, \(^{241}_{93}Np\)
d. Equation for A: 247+A = 254+(5*1)
A=12
Equation for Z: 97+Z = 102+(5*0)
Z=5
Therefore, the atom is Boron: \(^{12}_5B\)
e. Equation for A: 239+A = 246+(6*1)
A=13
Equation for Z: 93+Z = 99+(6*0)
Z=6
Therefore, the missing reactant is \(^{13}_6C\)
Q25.41E
Calculate the following questions regarding \(^{35}S\) isotope, given its half life is 88 days:
- What is the decay constant for \(^{35}S\)(in s-1)?
- How many atoms will disintegrate per second (the activity) of a 2.00 mg sample of \(^{35}S\) sample?
- After 176 days, what mass of the initial 2.00 mg sample will remain?
- What is the sample's rate of radioactive decay after 176 days?
A25.41E
a. Recall that radioactive decay is a first order reaction, subject to this equation:
\(\lambda= ln2/(t_{1/2})\)
So for part (a), we need to calculate for \(\lambda\), the rate constant. We simply plug in 88 for \(t_{1/2}\), to obtain \(\lambda=0.00787667\)
b. To find the activity of a 2.00 mg sample, we use the equation A=\(\lambda\)N, where N is the number of atoms in the sample. So we need to convert 2 mg of sulfur to atoms using molar mass and Avogadro's number:
(.002g Sulfur/32.066 g/mol)*(Avogadro's number) = 3.756*10^19 atoms in our sample.
Now we multiply by the decay constant, \(\lambda\)=0.00787667 to get 2.958*10^17 atoms disintegrating. But this is in units of \(days^{-1}\), as that was what our decay constant used. We need per second. So we divide this number by number of seconds in a day, 86400, and get 3.424*10^12 atoms disintegrating per second.
c. To determine how much of the initial amount remains, we should convert 176 days to half-lives of \(^{35}S\), because we are doing a radioactive decay problem. 176/88= 2 half lives. Now recall that for each half life that passes, one half of the original amount decays away. So after 1 half life, 1 mg would remain, and after 2 half lives, 0.5 mg would remain. Another way to write this is \(N=N_o(0.5)^{t}\), where N is the current amount, \(N_o\) is the original amount, and t is the number of half lives that pass. Therefore, our answer is \(2mg*(0.5)^2\)=0.5mg
d. The rate of decay after 176 days, or after 2 half lives, is determined by the equation: \(A=kN\) because activity is directly proportional to the number of atoms in a sample.
Therefore, we need to know how many atoms are present in the sample: as in part (b), we will use molar mass and Avogadro's number to calculate how many atoms are present: from part (c), we have 0.5 mg or 0.0005g.
\(\frac{.0005g}{32.066g/mol}\) = .00001559 mol S * Avogadro's number = 9.39*10^18 atoms remaining after 176 days.
We now multiply by our decay constant, \(\lambda\):
9.39*10^18 * 0.00787667=7.3962*10^16 disintegrations/day.
Divide by the number of seconds in a day, 86400, to obtain 8.56*10^11 disintegrations/second
Q21.2.26
Using the information provided, predict whether each reaction is favorable and the amount of energy released or required in megaelectronvolts and kilojoules per mole.
- alpha decay of oxygen-16
- alpha decay to produce chromium-52
A21.2.26
a. Typically, elements with mass numbers over 200 will undergo alpha decay. Furthermore, oxygen-16 has an even number of protons and neutrons, and a ratio between them of 1. For such a low atomic number, this is fairly stable. Therefore, it would require an input of energy to initiate this reaction, i.e. it is not favorable. Let us calculate the energy required:
First, we should write out the reaction: \(^{16}_{8}O \rightarrow ^4_2He + ^{12}_6C\)
Next, we use the masses of reactants and products, and find what the change in mass is, which will then be converted into energy according to Einstein's famous equation.
Total mass of reactants: Oxygen-16 has 8 protons and 16-8=8 neutrons and 8 electrons. Therefore, it has a mass of 8(1.007276)+8(1.008665)=16.127528 amu
Total mass of products: Carbon-12, by definition, has an atomic mass of 12 amu. An alpha particle has a mass of 4.001506 amu. So total=16.001506 amu
Difference: 16.127528 amu- 16.001506 amu = 0.126022 amu
This needs to be converted to kilograms, but for 1 mole of oxygen-16, that .126022 amu is actually 0.126022 g, or .000126022 kg, by definition of an amu
Now substitute this for m in Einstein's equation \(E=mc^2\):
E (in joules) = 0.000126022 kg*\((\frac{2.998*10^8 m}{s^2})^2\)= 1.1327 * \(10^{13}\) J/mol or 1.1327*\(10^{10}\)kJ/mol
Another handy way to convert this is due to the fact that 1 amu difference converts to 931 MeV. So for one atom of oxygen-16: 0.126022*931\(\frac{MeV}{amu}\) = 117.32648 MeV. Multiplied by Avogadro's number, we get 7.0654*\(10^{25}\)MeV/mol
b. Balancing the nuclear reaction, the equation of the reaction should look like this: \(^{56}_{26}Fe\rightarrow ^{52}_{24}Cr+^4_2He\)
Iron-56 is generally quite stable, so alpha decay is unlikely, making this an unfavored reaction. Let's calculate how much energy is required to induce this reaction, proceeding as before:
Total mass of reactants: Iron-56 has 26 protons and 30 neutrons. 26(1.007276)+30(1.008665)=56.449126 amu
Total mass of products: Chromium-52 has 24 protons and 28 neutrons: 24(1.007276)+28(1.008665)=52.417244 amu + 4.001506 amu = 56.41875 amu
Difference: 56.449126 amu - 56.41875 amu = 0.030376 amu.
We perform the same calculations as before:
0.030376 amu becomes 0.030376 kg/mol
0.030376*2.998*\(10^8 \frac{m}{s^2}\)=9.1067*\(10^6\)J/mol or 9.1067*\(10^3\)kJ/mol
Alternatively, 0.030376 amu*931\(\frac{MeV}{amu}\)=28.28 MeV * Avogadro's number = 1.703*\(10^{25}\)MeV
Q20.5.1
State whether you agree or disagree with this reasoning and explain your answer: Standard electrode potentials arise from the number of electrons transferred. The greater the number of electrons transferred, the greater the measured potential difference. If 1 mol of a substance produces 0.76 V when 2 mol of electrons are transferred—as in Zn(s) → Zn2+(aq) + 2e−—then 0.5 mol of the substance will produce 0.76/2 V because only 1 mol of electrons is transferred.
A20.5.1
This is absolutely false, as there is still the same potential, regardless of how many electrons are actually flowing across the reaction or in the cell.
\(E_o\) values don't rely on stoichiometric coefficients, as they are an intensive, not extensive, value.
For further reading on the topic, see:
[A]=[A]0−kt

