Energetics of Nuclear Reactions

Nuclear reactions are associated with changes in both mass and energy. In this module, the relationship between these two concepts are examined on a nuclear level.

Mass Defect and Binding Energy

Albert Einstein’s mass-energy equivalence relates energy and mass in nuclear reactions:

\[ E=mc^2 \label{Einstein} \]

Each time an energy change occurs, there is also a mass change that is related by the constant c² (the speed of light squared). Compared to the amount of energy due to the nuclear reaction, energy changes in chemical reactions are small, making the mass change insignificant for chemical reactions. However, on a nuclear level, there is a significant amount of energy change in comparison and therefore a discernible mass change. In Albert Einstein’s mass-energy equivalence (Equation \ref{Einstein}), “m” is the net change in mass in kilograms and “c” is a constant (the speed of light) in meters per second. Two common units to express nuclear energy are joules (\(J\)) and megaelectronvolts (\(MeV\)).

\[1.6022 \times 10^{-13}\, J = 1 \,MeV\]

The energy equivalent of 1 atomic mass unit (u), via Equation \ref{Einstein}, is:

\[\text{1 atomic mass unit (u)} = 1.4924 \times 10^{-10} J = 931.5\, MeV\]

By knowing the mass change in amu, the energy released can be directly calculated using these conversion factors, which have already taken into account mass conversions and the value of \(c^2\). Keep in mind that the sum of mass-energy equivalents of reactants and products must equal each other. Figure \(\PageIndex{1}\) provides an example of a mass defect. That is, the sum of the mass of the individual protons and neutrons differs from the overall mass of the nucleus. The nucleus weighs less than the masses of the individual subatomic particles.

Figure \(\PageIndex{1}\): There is a "mass deficient" in all nuclei (except 1H), where the sum of the masses of the individual nucleons is always greater than the mass of the nucleus. This corresponds to a nuclear binding energy via Einstein's formula (Equation \ref{Einstein}). (CC BY-NC; Ümit Kaya)

The sum of the mass and energy of the reactants are equivalent to the sum of the mass and energy of the products.

Where does this mass go when a nucleus is formed? Recall Einstein's mass-energy equivalence and how matter and energy are essentially different configurations of one another. Mass is lost and as a result, energy is released as the nucleons come together to form the nucleus. This energy is known as the nuclear binding energy. Einstein's mass-energy equivalence can be rewritten in the following terms:

\[\text{Nuclear Binding Energy} = \text{Mass Defect} \times c^2\]

or

\[E = Δm \times c^2 \label{Einstein2}\]

The mass is converted into the energy required to bind the protons and neutrons together to make a nuclei. Nuclear binding energy is also the defined as the energy required to break apart a nucleus.

Note that Δm can be either positive or negative (depends on where you set your zero point), but for our purposes, it will not really matter, and we should simply always use a positive mass deficit and say that is the energy released.

One additional thing to keep in mind is what a nucleus is and what a nucleon is. A nucleus (plural nuclei) is the center of the atom, and is composed of nucleon (which are both the protons and neutrons: a nucleon is what makes up the nuclei). This means the nucleus of an atom of Carbon-14 (¹⁴C)would contain 14 nucleons a nucleus of Uranium-238 (²³⁸U) would contain 238 nucleons etc.

Releasing Binding Energy

The mass number 60 is the maximum binding energy for each nucleon. (In other words, nuclei of mass number of approximately 60 require the most energy to dismantle). This means that the binding energy increases when small nuclei join together to form larger nuclei in a process known as nuclear fusion. For nuclei with mass numbers greater than 60, the heavier nuclei will break down into smaller nuclei in a process known as nuclear fission.

Figure \(\PageIndex{2}\): Binding energy curve (average binding energy per nucleon in MeV against number of nucleons in nucleus) for a number of relatively common (abundant) isotopes (not chosen systematically). A few important ones for the purposes of nuclear fusion and nuclear fission are marked, as well as iron-56, which sits at the highest point on this graph and cannot yield energy from fusion or fission. (Public Domain; Fastfission).

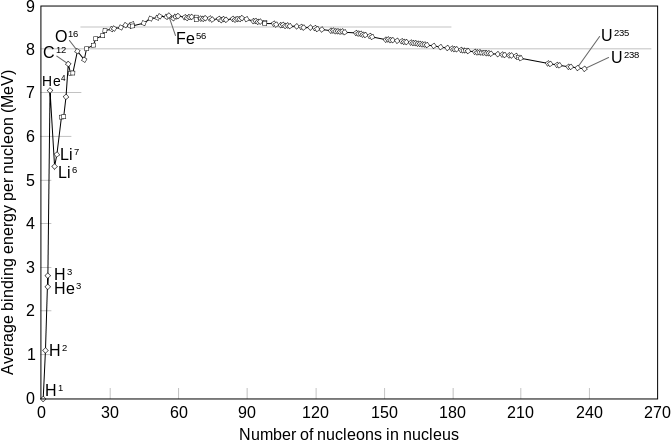
For fusion processes, the binding energy per nucleon will increase and some of the mass will be converted and released as energy (Figure \(\PageIndex{1}\)). Fission processes also release energy when heavy nuclei decompose into lighter nuclei. The driving force behind fission and fusion is for an atomic nuclei to become more stable. So nuclei with a mass number of approximately 60 will be the most stable, which explains why iron is the most stable element in the universe. Elements with mass numbers around 60 will also be stable elements, while elements with extremely large atomic masses will be unstable.

• Fusion of elements lighter than iron may release energy to generate nuclei with greater binding energy (per nucleon).
• Fission of elements heavier than iron may release energy to generate nuclei with greater binding energy (per nucleon).

Nuclear fusion can release more energy than nuclear fission, especially when fusing small nuclei like hydrogen and helium into bigger nuclei.

Exercise \(\PageIndex{1}\)

A certain nuclear reaction gives off 22.1 MeV. Calculate the energy released in Joules.

Answer

This is a simple conversion problem. Use 1.6022 x 10^-13J = 1MeV.

22.1 Mev x 1.6022 x 10^-13J/1 MeV = 3.54 x 10^-12 J

Exercise \(\PageIndex{2}\)

Suppose that the nuclear mass of ¹⁴N is reported as 13.998947 amu. Calculate the binding energy per nucleon.

Answer

Nitrogen-14 has 7 protons and 7 neutrons. The combined mass of the subatomic particles is

7 * (proton mass) + 7 * (neutron mass)
7 * (1.00728 amu) + 7 * (1.00866 amu ) = 14.11158 amu

The reported mass of Nitrogen is 13.998947 amu, so the mass defect (difference) is

14.11158 amu - 13.998947 amu = 0.112633 amu

Using Equation \ref{Einstein2},

E = ((0.112633g/1mol)(1kg/1000g)(1mol/6.022*10²³nuclei)(1nuclei/14nucleon)) x c² = 1.24 x 10^-12 J/nucleon

Exercise \(\PageIndex{3}\)

You have a pebble with a mass of 1.0 gram. If all of the mass was suddenly turned into energy, how much energy would be released?

Answer

The mass-energy equivalent of 1.0 gram is

E = .001 kg x ( 2.9979x10⁸ m/s )² = 9.0 x 10¹³ J.

This is roughly equal to the energy released by the Fat Man atomic bomb! Note that this problem tells us that it doesn't matter what's turned into the energy, if it happens, it will release the same amount of energy.

References

1. Petrucci, Ralph H., et al. "Energetics of Nuclear Reactions.” General Chemistry: Principles & Modern Applications. New Jersey: Pearson Education, Inc, 2007. 1052-1054.
2. Bloomfield, Louis A. How Things Work: The Physics of Everyday Life, Second Edition. New York: John Wiley & Sons, Inc., 2001 442-450
3. P. Khare, A. Swarup. "The Mass Difference and Nuclear Binding Energy." Engineering Physics: Fundamentals and Modern Applications: Massachusetts: Jones and Bartlett, 2010. 317