Nuclear Magic Numbers
- Page ID
- 1483
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Nuclear Stability is a concept that helps to identify the stability of an isotope. The two main factors that determine nuclear stability are the neutron/proton ratio and the total number of nucleons in the nucleus.
Introduction
A isotope is an element that has same atomic number but different atomic mass compared to the periodic table. Every element has a proton, neutron, and electron. The number of protons is equal to the atomic number, and the number of electrons is equal the protons, unless it is an ion. To determine the number of neutrons in an element you subtract the atomic number from the atomic mass of the element. Atomic mass is represented as (\(A\)) and atomic number is represented as (\(Z\)) and neutrons are represented as (\(N\)).
\[A=N + Z \label{1}\]
The principal factor for determining whether a nucleus is stable is the neutron to proton ratio. Elements with (\(Z<20\)) are lighter and these elements' nuclei and have a ratio of 1:1 and prefer to have the same amount of protons and neutrons.
Carbon has three isotopes that scientists commonly used: \( \ce{^12C}\), \( \ce{^13C}\), \( \ce{^14C}\). What is the the number of neutron, protons, total nucleons and \(N:Z\) ratio for the \( \ce{^12C}\) nuclide?
Solution
For this specific isotope, there are 12 total nucleons (\(A\)). From the periodic table, we can see that \(Z\) for carbon (any of the isotopes) is 6, therefore \(N=A-Z\) (from Equation \ref{1}):
\[12-6=6 \nonumber\]
The N:P ratio therefore is 6:6 or a 1:1. In fact 99% of all carbon in the earth is this isotope.
Identify the number of neutron, protons, total nucleons and N:Z ratio in the \( \ce{^12_8O}\) nuclide?
Elements that have atomic numbers from 20 to 83 are heavy elements, therefore the ratio is different. The ratio is 1.5:1, the reason for this difference is because of the repulsive force between protons: the stronger the repulsion force, the more neutrons are needed to stabilize the nuclei.
Neutrons help to separate the protons from each other in a nucleus so that they do not feel as strong a repulsive force from other.
Isotope Stability
The graph of stable elements is commonly referred to as the Band (or Belt) of Stability. The graph consists of a y-axis labeled neutrons, an x-axis labeled protons, and a nuclei. At the higher end (upper right) of the band of stability lies the radionuclides that decay via alpha decay, below is positron emission or electron capture, above is beta emissions and elements beyond the atomic number of 83 are only unstable radioactive elements. Stable nuclei with atomic numbers up to about 20 have an neutron:proton ratio of about 1:1 (solid line).
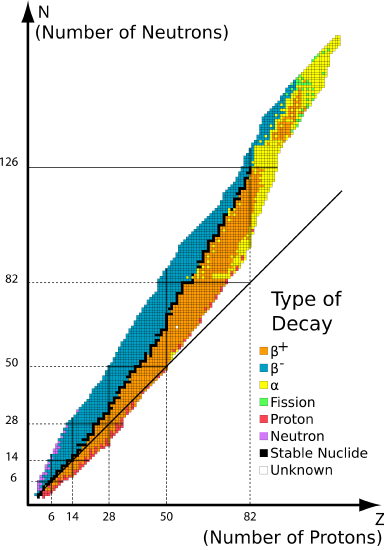
The deviation from the \(N:Z=1\) line on the belt of stability originates from a non-unity \(N:Z\) ratio necessary for total stability of nuclei. That is, more neutrons are required to stabilize the repulsive forces from a fewer number of protons within a nucleus (i.e., \(N>Z\)).
The belt of stability makes it is easy to determine where the alpha decay, beta decay, and positron emission or electron capture occurs.
- Alpha \(\alpha\) Decay: Alpha decay is located at the top of the plotted line, because the alpha decay decreases the mass number of the element to keep the isotope stable. This is accomplished by emitting a alpha particle, which is just a helium (\(\ce{He}\)) nucleus. In this decay pathway, the unstable isotope's proton number \(P\) is decreased by 2 and its neutron (\(N\)) number is decreased by 2. The means that the nucleon number \(A\) decreases by 4 (Equation \ref{1}).
- Beta \(\beta^-\) Decay: Beta \(\beta^-\) decay accepts protons so it changes the amount of protons and neutrons. the number of protons increase by 1 and the neutron number decreases by 1. This pathway occurs in unstable nuclides that have too many neutrons lie above the band of stability (blue isotopes in Figure \(\PageIndex{1}\)).
- Positron \(\beta^+\) Decay: Positron \(\beta^+\) emission and electron capture is when the isotope gains more neutrons. Positron emission and electron capture are below the band of stability because the ratio of the isotope has more protons than neutrons, think of it as there are too few protons for the amount of neutrons and that is why it is below the band of stability (yellow isotopes in Figure \(\PageIndex{1}\)).
As with all decay pathways, if the daughter nuclides are not on the Belt, then subsequent decay pathways will occur until the daughter nuclei are on the Belt.
Magic Numbers
The Octet Rule was formulated from the observation that atoms with eight valence electrons were especially stable (and common). A similar situation applies to nuclei regarding the number of neutron and proton numbers that generate stable (non-radioactive) isotopes. These "magic numbers" are natural occurrences in isotopes that are particularly stable. Table 1 list of numbers of protons and neutrons; isotopes that have these numbers occurring in either the proton or neutron are stable. In some cases there the isotopes can consist of magic numbers for both protons and neutrons; these would be called double magic numbers. The double numbers only occur for isotopes that are heavier, because the repulsion of the forces between the protons. The magic numbers are:
- proton: 2, 8, 20, 28, 50, 82, 114
- neutron: 2, 8, 20, 28, 50, 82, 126, 184
Also, there is the concept that isotopes consisting a combination of even-even, even-odd, odd-even, and odd-odd are all stable. There are more nuclides that have a combination of even-even than odd-odd. Just like there exist violations to the octet rule, many isotopes with no magic numbers of nucleons are stable.
| Proton number (Z) | Neutron Number | # of stable Isotopes |
|---|---|---|
| Even | Even | 163 |
| Even | Odd | 53 |
| Odd | Even | 50 |
| Odd | Odd | 4 |
Although rare, four stable odd-odd nuclides exist: \(\ce{^2_1H}\), \(\ce{^{6}_3Li}\), \(\ce{^{10}_5B}\), \(\ce{^{14}_7N}\)
Unstable or Stable
Here is a simple chart that can help you decide is an element is likely stable.
- Calculate the total number of nucleons (protons and neutrons) in the nuclide. If the number of nucleons is even, there is a good chance it is stable.
- Are there a magic number of protons or neutrons? 2,8,20,28,50,82,114 (protons), 126 (neutrons), 184 (neutrons) are particularly stable in nuclei.
- Calculate the N/Z ratio and use the belt of stability (Figure \(\PageIndex{1}\):) to determine the best way to get from an unstable nucleus to a stable nucleus
Using the above chart state if this isotope is alpha-emitter, stable, or unstable:
- \(\ce{^{40}_{20}Ca}\)
- \(\ce{^{54}_{25}Mn}\)
- \(\ce{^{210}_{84}Po}\)
- Answer
-
Add texts here. Do not delete this text first.
If the isotope is located above the band of stability what type of radioactivity is it? what if it was below?
- Answer
-
Based off the belt of stability:
- Stable, because this Ca isotope has 20 neutrons, which is on of the magic numbers
- Unstable, because there is an odd number (25 and 29) of protons and neutrons
- Alpha-emitter, because Z=84, which follows rule/step one on the chart
Carbon is stable
- Answer
-
Carbon is stable
Name one of the isotopes that consist of odd-odd combination in the nuclei?
- Answer
-
Hydrogen-2, Lithium-6, Boron-10, nitrogen-14
References
- Olmsted III, John and Gregory M William. Chemistry Fourth Edition. John Wiley and Sons Inc:NJ, 2006.
- Petrucci, Ralph H., William S. Harwood, F. Geoffrey Herring, Jeffry D Madura. General Chemistry. Pearson Education Inc: NJ, 2007.

