24: Kinetics

These are homework exercises to accompany the Textmap created for "General Chemistry: Principles and Modern Applications " by Petrucci et al. Complementary General Chemistry question banks can be found for other Textmaps and can be accessed here. In addition to these publicly available questions, access to private problems bank for use in exams and homework is available to faculty only on an individual basis; please contact Delmar Larsen for an account with access permission.

Q24.1A

In the reaction \(\ce{4A + 3B \rightarrow 2C + 3D}\) reaction \(\ce{A}\) is found to disappear at a rate of 5.1 X 10^-5 Ms^-1

1. What is the rate of reaction?
2. What is the rate of disappearance of \(\ce{B}\)?
3. What is the rate of formation of \(\ce{C}\)?

Kinetics

S24.1A

1. \(\mathrm{-\dfrac{1}{4} \left (\dfrac{-\Delta[A]}{\Delta t} \right ) = \dfrac{1}{4} (5.1 \times 10^{-5}\, Ms^{-1}) = 1.3 \times 10^{-5}\, Ms^{-1}}\)
2. Rate of disappearance of \(\ce{B}\) = reaction rate X coefficient of \(\ce{B}\)
   \(\mathrm{(1.3 \times 10^{-5}\,Ms^{-1})(3) = 3.9 \times 10^{-5}\, Ms^{-1}}\)
3. Rate of formation of \(\ce{C}\) = reaction rate X coefficient of \(\ce{C}\)
   \(\mathrm{(1.3 \times 10^{-5}\,Ms^{-1})(2) = 2.6 \times 10^{-5}\, Ms^{-1}}\)

Q24.1B

In the reaction \(\ce{3A + B \rightarrow 3C + 3D}\), \(\ce{A}\) has a disappearance rate of 3.4 × 10^-3 Ms^-1.

1. What is the rate of reaction at point \(\ce{A}\)?
2. What is the rate of disappearance of \(\ce{B}\)?
3. What is the rate of formation of \(\ce{C}\)?

S24.1B

For more help see: The Rate of a Chemical Reaction

1. \(\mathrm{-\dfrac{1}{3} \left( -\dfrac{\Delta[A]}{\Delta t}\right) = \dfrac13 (3.4 \times 10^{-3}\, Ms^{-1}) = 1.13 \times 10^{-3}\, Ms^{-1}}\)
2. \(\mathrm{\textrm{Rate of disappearance of B} = reaction\: rate \times coefficient\: of\: B}\)
   \(\mathrm{(1.13 \times 10^{-3}\,Ms^{-1})(1) = 1.13 \times 10^{-3}\,Ms^{-1}}\)
3. \(\mathrm{\textrm{Rate of formation of C} = reaction\: rate \times coefficient\: of\: C}\)
   \(\mathrm{(1.13 \times 10^{-3}\,Ms^{-1})(2) = 2.26 \times 10^{-3}\, Ms^{-1}}\)

Q24.1C

For the reaction \(\mathrm{3A + 2B \rightarrow C + 2D}\) reactant \(\ce{A}\) is found to disappear at the rate of 4.6 X 10^-5 Ms^-1

1. What is the rate of reaction?
2. What is the rate of disappearance of the reactant \(\ce{B}\)?
3. What is the rate of appearance for product \(\ce{D}\)?

S24.1C

1. \(\mathrm{-\dfrac{1}{3} \left(\dfrac{- \Delta[A]}{\Delta t}\right) = \dfrac{1}{3} (4.6 \times 10^{-5}\, Ms^{-1}) = 1.5 \times 10^{-5}\, Ms^{-1}}\)
2. Rate disappearance of \(\mathrm{B = (rate\: of\: reaction) \times 2(coefficient\: of\: B)}\)
   \(\mathrm{(1.5 \times 10^{-5}\,Ms^{-1})(2) = 3.1 \times 10^{-5}\, Ms^{-1}}\)
3. Same process as B) (multiply rate of reaction by 2) OR:
   Rate of appearance of \(\mathrm{D = -\dfrac{1}{3}(2)\left(\dfrac{\Delta[A]}{\Delta t}\right) = -\dfrac{2}{3}(4.6 \times 10^{-5}\, Ms^{-1}) = 3.1 \times 10^{-5}\, Ms^{-1}}\)

Q24.3A

In the reaction \(\ce{A \rightarrow B}\), \(\ce{[A]}\) is found to be 0.750 M at \(\mathrm{t = 61.2\, s}\) and 0.704 M at \(\mathrm{t = 73.5\, s}\). Determine the average rate of the reaction during this time interval.

Kinetics

S24.3A

\(\mathrm{-\dfrac{\Delta[A]}{\Delta t} = \dfrac{0.704\,M-0.750\,M}{61.2\,s-73.5\,s} = 3.7 \times 10^{-3}\, M s^{-1}}\)

Q24.3B

What is the average rate of reaction over a time interval for \(\ce{[A]}\) if it is 0.455 M at \(\mathrm{t = 80.25\, s}\) and 0.474 M at \(\mathrm{t = 82.4\, s}\)?

S24.3B

For more help see: The Rate of a Chemical Reaction

\(\mathrm{-\dfrac{\Delta[A]}{\Delta t} = \dfrac{0.474\,M-0.455\,M}{82.4\,s-80.25\,s} = 8.8 \times 10^{-3}\, Ms^{-1}}\)

Q24.3C

In the reaction \(\mathrm{A \rightarrow B}\), \(\mathrm{[A]}\) is found to be 0.675M at \(\mathrm{t = 51.1\,s}\) and 0.605M at \(\mathrm{t = 61.5\,s}\). Find the average rate of the reaction during this time interval.

S24.3C

\(\mathrm{Rate = -\left(\dfrac{\Delta[A]}{\Delta t}\right) = \dfrac{0.675\,M-0.605\,M}{61.5\,s-51.1\,s} = 0.00673 = 6.73 \times 10^{-3}\, Ms^{-1}}\)

Q24.4A

In the reaction \(\mathrm{A \rightarrow products}\), at \(\mathrm{t = 0}\), \(\mathrm{[A]=0.1563\,M}\). After 1.00 minute, \(\mathrm{[A]=0.1496\,M}\), and after 2.00 minutes, \(\mathrm{[A]=0.1431\,M}\).

1. Calculate the average rate of reaction during the first minute and during the second minute.
2. Why are these two rates not equal?

Q24.5A

In the reaction \(\mathrm{A \rightarrow products}\), 4.50 minutes after the reaction is started, \(\mathrm{[A]=0.587\,M}\). The rate of reaction at this point is \(\mathrm{rate = -\dfrac{\Delta[A]}{\Delta t} = 2.1 \times 10^{-2}\, M\, min^{-1}}\). Assume that this rate remains constant for a short period of time.

1. What is \(\mathrm{[A]}\) 6.00 minutes after the reaction is started?
2. At what time after the reaction is started with \(\mathrm{[A] = 0.56\,M}\)?

Q24.7A

For the reaction \(\mathrm{A + 2B \rightarrow 2C}\), the rate of reaction is 1.75 x 10^-5 M s^-1 at the time when \(\mathrm{[A] = 0.3575\,M}\).

1. What is the rate of formation of \(\mathrm{C}\)?
2. What will \(\mathrm{[A]}\) be 1 minute later?
3. Assume the rate remains at 1.75 x 10^-5M s^-1. How long would it take for \(\mathrm{[A]}\) to change from 0.3580 to 0.3500M?

Q24.10A

At 65°, the half-life for the first-order decomposition of \(\ce{N2O5(g)}\) is 2.35 minutes.

\(\ce{N2O5(g) \rightarrow 2NO2(g) + \dfrac{1}{2}O2(g)}\)

If 1.00g of \(\ce{N2O5}\) is introduced into an evacuated 10L flask at 65°C,

1. What is the initial partial pressure, in mmHg, of \(\ce{N2O5(g)}\)?
2. What is the initial partial pressure, in mmHg, of \(\ce{N2O5(g)}\) after 2.35 minutes?
3. What is the total gas pressure, in mmHg, after 2.35 minutes?

Q24.11A

The initial rate of the reaction \(\ce{A + B \rightarrow C + D}\) is determined for different initial conditions, with the results listed in the table.

1. What is the order of reaction with respect to \(\ce{A}\) and to \(\ce{B}\)?
2. What is the overall reaction order?
3. What is the value of the rate constant, \(\ce{k}\)?

Expt	\(\ce{[A]}\),M	\(\ce{[B]}\),M	Initial Rate, M s^-1
1	0.185	0.144	3.35 x 10^-4
2	0.185	0.288	1.35 x 10^-3
3	0.370	0.144	6.75 x 10^-4
4	0.370	0.288	2.70 x 10^-3

Q24.11B

The initial rate of the reaction \(\ce{A + B \rightarrow C + D}\) is determined for different initial conditions, with the results listed in the table:

Expt	\(\ce{[A]}\), M	\(\ce{[B]}\), M	Initial Rate, Ms^-1
1	0.331	0.203	2.205 X 10^-4
2	0.331	0.406	8.82 X 10^-4
3	0.662	0.203	4.41 X 10^-4
4	0.662	0.406	1.7 X 10^-3

1. What is the order of reaction with respect to \(\ce{A}\) and \(\ce{B}\)?

 

b. What is the overall reaction order?

c. What is the value of the rate constant \(\ce{k}\)?

S11B

1. \(\mathrm{Reaction\, 1 = 2.205 \times 10^{-4} = k \times [0.331]^m [0.203]^n}\)
   \(\mathrm{Reaction\, 2 = 8.82 \times 10^{-4} = k \times [0.331]^m [0.406]^n}\)
   \(\mathrm{Reaction\, 3 = 4.41 \times 10^{-4}= k \times [0.662]^m [0.203]^n}\)
   \(\mathrm{Reaction\, 4 = 1.7 \times 10^{-3}= k \times [0.662]^m [406]^n}\)

Order of Reaction with respect to B:

1. Find where \(\ce{A}\) is constant and \(\ce{B}\) changes (Reaction 1 and Reaction 2)
2. Divide: \(\mathrm{\dfrac{Reaction\, 2}{Reaction\, 1} = \dfrac{8.82 \times 10^{-4}}{ 2.205 \times 10^{-4}} = \dfrac{[0.331]^m [0.406]^n}{[0.331]^m[0.203]^n}}\)
   \(\mathrm{\dfrac{Reaction\, 2}{Reaction\, 1}= 4 = 2^n \rightarrow n=2}\)
3. Thus the reaction is second order with respect to \(\ce{B}\).

Order of Reaction with respect to A:

1. Find where \(\ce{B}\) is constant and \(\ce{A}\) changes (Reaction 3 and Reaction 1)
2. Divide: \(\mathrm{\dfrac{Reaction\, 3}{Reaction\, 1} = \dfrac{4.41 \times 10^{-4}}{ 2.205 \times 10^{-4}} = \dfrac{[0.406]^m[0.662]^n}{[0.203]^m[0.662]^n}}\)
   \(\mathrm{\dfrac{R3}{R1} = 2 = 2^m}\)
   \(\mathrm{m = 1}\)
3. Thus the reaction is first order with respect to \(\ce{A}\)

2. Reaction order = reaction order of A + reaction order of B = 3^rd order reaction
3. \(\mathrm{2.205 \times 10^{-4} = k \times [0.331][0.203]^2}\)
   \(\mathrm{k=1.6 \times 10^{-2}}\)

Q24.11C

Use the table below to answer the following questions:

1. Find the order of the reaction \(\ce{A}\) vs. \(\ce{B}\)
2. Find the overall order
3. Find the rate constant

EXPT	\(\ce{[A]}\),M	\(\ce{[B]}\),M	Initial Rates, Ms^-1
1	0.175	0.138	3.75 × 10^-4
2	0.175	0.185	1.25 × 10^-3
3	0.365	0.138	3.75 × 10^-4
4	0.365	0.185	1.25 × 10^-3

S24.11C

For more help see: The Rate of a Chemical Reaction

\(\mathrm{Reaction\: 1 =3.75 \times 10^{-4} = k \times [0.175]^m [0.138]^n}\)

\(\mathrm{Reaction\: 2 =1.25 \times 10^{-3} = k \times [0.175]^m [0.185]^n}\)

\(\mathrm{Reaction\: 3 =3.75 \times 10^{-4}= k \times [0.365]^m [0.138]^n}\)

\(\mathrm{Reaction\: 4 =1.25 \times 10^{-3}= k \times [0.365]^m [0.185]^n}\)

1. Order of reaction with respect to B:
   1. Find where \(\ce{A}\) is constant and \(\ce{B}\) changes (Reaction 1 and Reaction 2)
   2. Divide: \(\mathrm{\dfrac{Reaction\: 2}{Reaction\: 1} = \dfrac{1.25 \times 10^{-3}}{ 3.75 \times 10^{-4}} = \dfrac{[0.175]^m [0.185]^n}{[0.175]^m[0.138]^n}}\)
   \(\mathrm{\dfrac{Reaction\: 2}{Reaction\: 1}= 4 = 2^n \rightarrow n=2}\)
   3. Therefore the reaction is second order with respect to \(\ce{B}\).
   
   Order of reaction with respect to A:
   1. Find where \(\ce{B}\) is constant and \(\ce{A}\) changes (Reaction 3 and Reaction 1)
   2. Divide: \(\mathrm{\dfrac{Reaction\: 3}{Reaction\: 1} = \dfrac{4.41 \times 10^{-4}}{ 2.205 \times 10^{-4}} = \dfrac{[0.406]^m[0.662]^n}{[0.203]^m[0.662]^n}}\)
   \(\mathrm{\dfrac{R3}{R1} = 2 = 2^m}\)
   \(\mathrm{m = 1}\)
   3. Thus the reaction is first order with respect to \(\ce{A}\)
2. \(\mathrm{Reaction\: order = \textrm{reaction order of A} + \textrm{reaction order of B} = 3^{rd}\textrm{ order reaction}}\)
3. \(\mathrm{2.205 \times 10^{-4} = k \times [0.331][0.203]^2}\)
   \(\mathrm{k=1.6 \times 10^{-2}}\)

Q11D

The initial rate of the reaction \(\mathrm{A + B \rightarrow C + D}\) is determined for difference initial conditions, with the results listed in the table:

Expt	\(\mathrm{[A]}\), M	\(\mathrm{[B]}\), M	Initial Rates, Ms^-1
1	0.241	0.153	1.261 X 10^-4
2	0.241	0.306	5.044 X 10^-4
3	0.482	0.153	2.522 X 10^-4
4	0.482	0.306	6.741 X 10^-4

1. What is the order of the reaction with respect of \(\mathrm{A}\) and \(\mathrm{B}\)? Write out respective rate laws for \(\mathrm{A}\) and \(\mathrm{B}\)
2. What is the overall reaction order?
3. What is the value of the \(\ce{k}\), the rate constant?

S24.11D

1. m and n are the respective orders according to \(\mathrm{A}\) and \(\mathrm{B}\):
   \(\mathrm{R1 = 1.261 \times 10^{-4} = [0.241]^m[0.153]^n}\)
   \(\mathrm{R2 = 5.044 \times 10^{-4} = [0.241]^m[0.306]^n}\)
   \(\mathrm{R3 = 2.522 \times 10^{-4} = [0.482]^m[0.153]^n}\)
   \(\mathrm{R4 = 6.741 \times 10^{-4} = [0.482]^m[0.306]^n}\)
   Now utilize the rate laws / solve:
   Divide reaction 2 by reaction 1 (\(\mathrm{A}\) is constant \(\mathrm{B}\) changes concentration)
   \(\mathrm{\dfrac{R2}{R1} = \dfrac{5.044 \times 10^{-4}}{1.261 \times 10^{-4}} = \dfrac{[0.241]^m[0.306]^n}{[0.241]^m[0.151]^n}}\)
   \(\mathrm{\dfrac{R2}{R1} = 4 = 2^n}\)
   \(\mathrm{n = 2}\)
   Reaction is second order with respect to \(\mathrm{B}\). Do the same for \(\mathrm{A}\). Use reactions 3 and 1 (\(\mathrm{[B]}\) is constant, \(\mathrm{[A]}\) changes)
   \(\mathrm{\dfrac{R3}{R1} = \dfrac{2.522 \times 10^{-4}}{1.26 \times 10^{-4}} = \dfrac{[0.482]^m[0.153]^n}{[0.241]^m[0.153]^n}}\)
   \(\mathrm{\dfrac{R3}{R1} = 2 = 2^m}\)
   \(\mathrm{m = 1}\)
   Reaction is first order with respect to \(\mathrm{A}\)
2. Overall reaction order = (reaction order of A + reaction order of B) = 1 + 2 = 3rder order overall
3. Substitute in for one of the reactions
   \(\mathrm{Rate\: law = k[A][B]^2}\)
   For example use reaction 1
   Rate: \(\mathrm{1.261 \times 10^{-4} = k[A][B]^2}\)
   \(\mathrm{1.261 \times 10^{-4} = k[0.241][0.153]^2}\)
   \(\mathrm{k = 0.0224\, M^{-2}s^{-1}}\)

Q24.12A

For the reaction \(\ce{A + B \rightarrow C + D}\) the following initial rate of reaction were found. What is the rate law for this reaction?

Expt	\(\ce{[A]}\),M	\(\ce{[B]}\),M	Initial Rate, M min^-1
1	0.60	1.80	4.2 x 10^-3
2	1.80	1.80	1.3 x 10^-2
3	3.60	3.60	5.2 x 10^-2

Q24.12B

For the reaction A + B àC+ D the following initial rate of reaction were found. What is the rate law for this reaction?

Rate = 2.16 x 10^-3M²min[A]¹[B]²

Expt	[A],M	[B],M	Initial Rate, M min^-1
1	0.60	1.80	4.2 x 10^-3
2	1.80	1.80	1.3 x 10^-2
3	0.60	3.60	1.7 x 10^-2

Q24.13A

The following rates of reaction were obtained in three experiments with the reaction \(\ce{2NO(g) + Cl2(g) \rightarrow 2NOCl (g)}\).

Expt	Initial [NO], M	Initial [Cl2], M	Initial Rate of Reaction, M s^-1
1	0.0125	0.0260	2.23 x 10^-5
2	0.0125	0.0510	4.50 x 10^-5
3	0.0250	0.0260	9.05 x 10^-5

What is the rate of law of this reaction?

S24.13A

Order on [NO]= 2, rate quadruples for double in concentration
Order on [Cl2]= 1, rate doubles for double in concentration

RATE= k[NO]^2[Cl2]

Q24.13B

The following rates of reaction were obtained in three experiments with the reaction 2NO(g) + Cl₂(g) à2NOCl (g).

Expt	Initial [NO], M	Initial [Cl2], M	Initial Rate of Reaction, M s^-1
1	0.0125	0.0255	2.23 x 10^-5
2	0.0125	0.0510	4.46 x 10^-5
3	0.0250	0.0255	8.92 x 10^-5

What is the rate law of this reaction?

S24.13B

Rate = 5.597 M²sec[NO]²[Cl₂]¹

Q24.13C

The following rates of reactions were obtained in three experiments with the reaction \(\ce{2NO(g) + Cl2(g) \rightarrow 2NOCl(g)}\)

	Expt			Initial \(\ce{[NO]}\), M			Initial \(\ce{Cl2}\), M			Initial rate of reaction, Ms^-1
1	0.145	0.405	1.24 X 10^-5
2	0.145	0.81	2.48 X 10^-5
3	0.29	0.405	4.96 X 10^-5

What is the rate law for this reaction?

Kinetics

S24.13C

Order of Reaction with respect to [Cl₂]:

1. Find where \(\ce{[NO]}\) is constant and \(\ce{[Cl2]}\) changes (Reaction 1 and Reaction 2)
2. Divide: Reaction 2 by Reaction 1
   \(\mathrm{\dfrac{2.48 \times 10^{-5}}{1.24 \times 10^{-5}}= \dfrac{[0.145]^m[0.81]^n}{[0.145]^m[0.405]^n} \rightarrow 2 = 2^n}\)
3. Thus \(\ce{[Cl2]}\) is first order

Order of Reaction with respect to [NO]:

1. Find where \(\ce{[Cl2]}\) is constant and \(\ce{[NO]}\) changes (Reaction 1 and Reaction 3)
2. Divide: Reaction 3 by Reaction 1
   \(\mathrm{\dfrac{4.96 \times 10^{-5}}{1.24 \times 10^{-5}} = \dfrac{[0.29]^m [0.405]^n}{[0.145]^m[0.405]^n} \rightarrow 4=2^m}\)
3. Thus \(\ce{[NO]}\) is second order

Rate Law:

\(\mathrm{Rate\, Law = k[NO]^2[Cl_2]}\)

Q24.13D

Use the date table below to determine the rate law of the reacton: \(\ce{A + B \rightarrow 2D}\)

Experiment	Initial \(\ce{[A]}\),M	Initial \(\ce{[B]}\),M	Initial Rate of Reaction, Ms^-1
1	1.5	1.5	4.3 × 10^-3
2	1.5	3.0	8.6 × 10^-3
3	3.0	3.0	1.12 × 10^-2

S24.13D

For more help see: The Rate of a Chemical Reaction

From looking at the table, \(\ce{[A]}\) is first order and \(\ce{[B]}\) is first order

overall rxn is 2nd order

\(\mathrm{R= k[A][B]}\)

\(\mathrm{4.3E\textrm{-3}\,Ms^{-1}= k(1.5\,M)(1.5\,M)}\)

\(\mathrm{k=1.2E\textrm{-3}\,(M^{-1})(s^{-1})}\)

Q24.13E

The following rates of reactions were obtained in three experiments with the reaction \(\ce{2NO(g) + Cl2 \rightarrow 2NOCl(g)}\)

Expt	Initial \(\ce{[NO]}\), M	Initial \(\ce{[Cl2]}\), M	Initial Rate of reaction Ms^-1
1	0.362	0.730	1.45 X 10 ^-5
2	0.362	1.46	2.90 X 10^-5
3	0.724	.730	5.80 X 10^-5

What is the order of the reaction with respect of \(\ce{A}\) and \(\ce{B}\)? Write out respective rate laws for \(\ce{A}\) and \(\ce{B}\)

S24.13E

m and n are the respective orders according to \(\ce{A}\) and \(\ce{B}\):

\(\mathrm{R1 = 1.45 \times 10^{-5} = [0.362]^m[0.730]^n}\)

\(\mathrm{R2 = 2.90 \times 10^{-5} = [0.362]^m[1.46]^n}\)

\(\mathrm{R3 = 5.80 \times 10^{-5} = [0.724]^m[0.730]^n}\)

Now utilize the rate laws and solve:

Divide R2 by R1 (\(\ce{[A]}\) stays constant while \(\ce{[Cl2]}\) changes)

\(\mathrm{\dfrac{R2}{R1} = \dfrac{2.9 \times 10^{-5}}{1.45 \times 10^{-5}} = \dfrac{[0.362]^m[1.46]^n}{[0.362]^m[0.730]^n}}\)

\(\mathrm{\dfrac{R2}{R1} = 2 = 2^n}\)

\(\mathrm{n = 1}\)

First order with respect to \(\ce{Cl2}\)

Divide R3 by R1 (\(\ce{[Cl2]}\) is constant \(\ce{[NO]}\) changes)

\(\mathrm{\dfrac{R3}{R1} = \dfrac{5.8 \times 10^{-5}}{1.45 \times 10^{-5}} = \dfrac{[0.724]^m[0.730]^n}{[0.362]^m[0.730]^n}}\)

\(\mathrm{\dfrac{R3}{R1} = 4 = 2^m}\)

\(\mathrm{n = 2}\)

Second order with respect to \(\mathrm{[NO]}\)

 

\(\mathrm{Rate\: Law = k[NO]^2[Cl_2]}\)

Using the rate law we can solve for \(\ce{k}\), the rate constant

Use any set of experimental data

Lets use exp. 2

\(\mathrm{2.9 \times 10^{-5}\, Ms^{-1} = k[NO]^2[Cl_2] = k[0.362]^2[1.46]}\)

\(\mathrm{k = 1.52 \times 10^{-4}\, M^{-2}s^{-1} [NO]^2[Cl_2]}\)

Q24.14A

The following was obtained for the initial rates of reaction in the reaction \(\ce{A + 2B + C \rightarrow 2D + E}\).

Expt	Initial \(\ce{[A]}\),M	Initial \(\ce{[B]}\),M	\(\ce{[C]}\), M	Initial Rate
1	1.20	1.20	1.00	\(\ce{R1}\)
2	0.60	1.20	1.00	\(\ce{R2= \dfrac{1}{2} \times R1}\)
3	0.60	0.60	1.00	\(\ce{R3 = \dfrac{1}{4} \times R2}\)
4	1.20	1.20	0.50	\(\ce{R4 = 16 \times R3}\)
5	0.60	0.60	0.50	\(\ce{R5 = ?}\)

1. What are the reaction orders with respect to \(\ce{A}\), \(\ce{B}\), and \(\ce{C}\)?

For the reactant A, we need to compare the experiment 1 and 2, because in these two experiment, only the concentration of [A] changes.

As we can see, when we half the concentration of [A], the overall rate is halfed.

Therefore, the reaction order of [A] is 1.

For the reaction B, we can compare the experiment 2 and 3 for the same reason as before.

When the concentration of B is halfed, the overall rate is fourth of the initial rate.

Thus, we can determine that the reaction order of [B] is 1.

For the reactant C, we are going to compare the experiment 1 and 5.

We can tell that as the concentration of C is 1/2 as before, the overall initial rate is 16 times as before .

Therefore, we can say that the reaction order of [C] is －0.3.

b. What is the value of \(\ce{R5}\) in terms of \(\ce{R1}\)?

From question a, we know that the reaction order for [c] is -0.3, and the concentration of all the reactant is 1/2 as before.

Thus we can know R₅= 1/2 ^. 1/2 ^. -0.3 ^. [R₁]

Q24.14B

The following was obtained for the initial rates of reaction in the reaction A + 2B + C à2D + E.

Expt	Initial [A],M	Initial [B],M	[C], M	Initial Rate
1	1.20	1.20	1.00	R1
2	0.60	1.20	1.00	R2= ½ x R1
3	0.60	0.60	1.00	R3 = ¼ x R2
4	1.20	1.20	0.50	R4 = 16 x R3
5	0.60	0.60	0.50	R5 = ?

1. a) What are the reaction orders with respect to A, B, and C?
2. b) What is the value of R₅ in terms of R₁?

S24.14A

[A] = 1^st order

[B] = 2^nd order

[C] = 1^st order

R₅ = ½ R

Q24.15A

One of the following statements is true and the other is false regarding the first-order reaction \(\ce{A \rightarrow B + C}\). Identify the true statement and the false one, and explain your reasoning.

1. The rate of the reaction decreases as more of \(\ce{B}\) and \(\ce{C}\) form.
2. The time required for one-half of substance \(\ce{A}\) to react is directly proportional to the quantity of \(\ce{A}\) present initially.

S24.15B

1. True: Since rate = k[A]¹; if [A] decreases, the rate will drop.
   
   I believe there is a typo in the proposed reaction and it should read A---->B+C. If this is the case, then A is the only reactant that decomposes into two products. Thus, if the concentration of the only reaction decreases, the rate will decrease as a result.
   
   Since it is a first order reaction, the rate is directly proportional to the species concentration. This means that changing the concentration of the reactant will alter the rate. We have to understand that the value of k is a rate constant value which means it doesn't change. The [A] is raised to the first power so any value in the brackets will stay the same and wont be affected by the superscript.
   
   We can plug in imaginary values into the equation to make things easier, for example:
   
   If the original rate was: rate=9.0*10^-3[2.0M]^1 , we could solve it through basic multiplication and find that the rate is 0.018s^-1.
   If we decrease [A] to 1.0M: rate=9.0*10^-3[1.0M]^-1 , we would find that the rate is 0.009s^1.
   
   Lastly, if you are wondering how to find the units use this equation: k units=(concentration)^-(w-1) x (s)^-1. W is the overall order of the reaction. in this case it is 1 so:
   -(1-1)=0 therefore we won't include a concentration label. Instead we use s^-1 by itself. Sometimes the time measurement can be in other units like minutes.
2. False: Since rate = k[A]¹; as the [A] drops, the reaction rate becomes disproportional to the concentration. Reaction starts fast at high concentrations but will slow down at low [A]. As I showed above, concentrations are not directly proportional to each other but, in first order reactions, are directly proportional to the rate instead. Any change in a first order concentration, shown by the example in part 1, can result in a change in the rate in general.
   
   One thing we can do, is use a formula to calculate the time it would take to reach one half of concentration A although it wont be directly proportional to the initial concentration of the substance. Below is an example of how this can be done with different values:
   
   
   
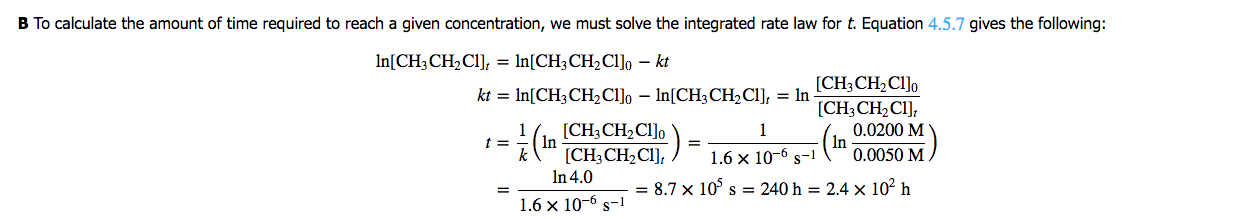
   If we determine [CH3CH2Cl]o as [A]o and [CH3CH2Cl]t as [A]t, or 1/2 [A], we can solve for t, time. If we assume [A]o to be 2.0M and [A]t to be 1/2 of 2, 1.0M, we can plug values into the formula and come to a conclusion. We would have to use the value given in part 1 for k, however.

Q24.16A

One of the following statements is true and the other is false regarding the first-order reaction \(\ce{4A \rightarrow B + C}\). Identify the true statement and the false one, and explain your reasoning.

1. A graph of \(\ce{[A]}\) versus time is a straight line.
2. The rate of the reaction is one half the rate of disappearance of \(\ce{A}\).

Q24.16B

One of the following statements is true and the other is false regarding the first-order reaction 2A àB + C. Identify the true statement and the false one, and explain your reasoning.

1. A graph of [A] versus time is a straight line.
2. The rate of the reaction is one half the rate of disappearance of A.

S24.16B

1. False: Since rate=k[A]¹; as [A] decreases, time and concentration become disproportional and graph will curve.
2. True: Since rate is dependent on balanced coefficients. [A] is actually twice the amount in rate = k[A]

Q24.17A

The first-order reaction \(\mathrm{A \rightarrow products}\) has \(\mathrm{t_{1/2} = 300\, s}\)

1. What percent of sample A remains unreacted 1000 s after the reaction starts?
2. What is the rate of reaction when \(\mathrm{[A] = 0.25\,M}\)

Kinetics

S24.17A

1. \(\mathrm{\ln(\%\, unreacted) = -kt}\)
   \(\mathrm{k = \dfrac{\ln 2}{t_{1/2}} = \dfrac{\ln 2}{300\,s} = 0.0023\, s^{-1}}\)
   \(\mathrm{ln(\%\, unreacted) = -(0.0023\,s^{-1})(1000\,s) = -2.3}\)
   \(\mathrm{e^{-2.3} = 0.1 \times 100\% = 10\%\, unreacted}\)
2. \(\mathrm{Rate = k[A]}\)
   \(\mathrm{Rate = 0.0023\,s^{-1}[0.25\,M] = 5.74 \times 10^{-4}\, Ms^{-1}}\)

Q24.17B

A first order reaction \(\ce{A \rightarrow products}\) has a half life of 120 seconds calculate the following:

1. What percentage of \(\ce{A}\) remains unreacted after 800 seconds of reaction.
2. What is the rate of reaction at \(\mathrm{[A] = 0.25\, M}\)?

S24.17B

For more help see: The Rate Law

1. \(\mathrm{t_{1/2} (first\: order) = \dfrac{\ln 2}{k}}\)
   \(\mathrm{k = \dfrac{\ln 2}{t_{1/2}} = \dfrac{\ln 2}{120\: s} = 5.77\times10^{-3}}\)
   percent unreacted defined by \(\mathrm{\dfrac{[A]_t}{[A]_0}}\)
   \(\begin{align}
   \mathrm{\dfrac{[A]_t}{[A]_0}} &= \mathrm{e^{-kt}}\\
   &= \mathrm{e^{\large{(-5.77\times10^{-3}\times800)}} \times 100 = 0.98\% \:remains\: unreached.}
   \end{align}\)
2. For a first order reaction, \(\mathrm{rate = k[C]}\)
   \(\mathrm{= 0.0046/s \times 0.25 }\)
   \(\mathrm{= 1.15\times10^{-3}\, M/s}\)

Q24.17C

The first order reaction has t_1/2 of 250s

1. What percent of a sample of \(\ce{A}\) remains unreacted 1500s after a reaction starts.
2. What if the rate of the reaction is 1/2 the rate of disappearance of \(\ce{A}\).

S24.17C

a. If t_\frac 12 = 250 seconds, and \(\mathrm{k ={0.693}{250\,s}

Q24.19A

The reaction \(\mathrm{A \rightarrow products}\) is first order in \(\ce{A}\)

1. If 4.2g \(\ce{A}\) decomposes for 45 minutes, the undecomposed \(\ce{A}\) is measured to be 1.05g. What is the half-life, \(\mathrm{t_{1/2}}\), of this reaction?
2. Starting with the same 4.2 g, what is the mass of undecomposed \(\ce{A}\) after 75 minutes?

S24.19A

1. \(\mathrm{(4.2\,g)\left (\dfrac{1}{4}\right ) = 1.05\,g \rightarrow 2}\) halflives have passed \(\mathrm{\rightarrow \dfrac{45\, minutes}{2} = t_{1/2} = 22.5\, minutes}\)
2. \(\mathrm{\dfrac{\ln[A]_t}{\ln[A]_0} = -kt}\)
   \(\mathrm{k = \dfrac{\ln 2}{t_{1/2}} = \dfrac{\ln 2}{22.5\, minutes} = 0.0308\, min^{-1}}\)
   \(\mathrm{\dfrac{\ln[A]_t}{\ln[A]_0}= (-0.0308\, min^{-1})(75\, min) = -2.31}\)
   \(\mathrm{[A]_t = [A]_0 e^{-2.31}}\)
   \(\mathrm{[A]_t = (4.2\,g)(0.09926) = 0.417\, g\, A}\)

Q24.19B

Consider another first order reaction \(\mathrm{A \rightarrow products}\).

1. 5g of \(\ce{A}\) is allowed to decompose for 45 minutes leaving 0.8 grams excess. What is the half life?
2. If we start with 1.8g of \(\ce{A}\) how much is remaining after 1 hour?

S24.19B

For more help see: The Rate Law

1. First we determine the value of \(\ce{k}\)
   \(\mathrm{ln\dfrac{[A]_t}{[A]_0}= -kt}\)
   \(\mathrm{ln\dfrac{[0.8]}{[5]}= -k(45\,min)}\)
   \(\mathrm{k= 4.07E\textrm{-2}\, min^{-1}}\)
   Next, we find the half life
   \(\begin{align}
   \mathrm t_{1/2} &= \mathrm{\dfrac{0.693}{k}}\\
   &= \mathrm{\dfrac{0.693}{4.07E\textrm{-2}}}\\
   &= \mathrm{17\, mins}
   \end{align}\)

Q24.19C

The reaction A to product is first order in \(\ce{A}\).

1. If 2.4 g of \(\ce{A}\) is allowed to decompose for 30 minutes, the mass of \(\ce{A}\) remaining undecomposed is found to be .6g. What is the halflife, t_1/2, of this reaction.
2. Starting with 2.4g of \(\ce{A}\) what is the mass of \(\ce{A}\) remaining undecomposed after 1 hour

S24.19C

1. Mass has decreased to 1/4 of the original mass. Since \(\mathrm{\left(\dfrac{1}{2}\right)\left(\dfrac{1}{2}\right) = \dfrac{1}{4}}\). 2 halflives have elapsed. As a result \(\mathrm{2 \times t_{1/2} = 30\: minutes}\)
   \(\mathrm{t_{1/2} = 15\: minutes}\)
2. \(\mathrm{k = \dfrac{0.693}{15\:minutes} = 0.0462\: min^{-1}}\)
   Use equation \(\mathrm{\dfrac{\ln[A]_t}{\ln[A]_0} = -kt}\)
   \(\mathrm{\dfrac{\ln[A]_t}{\ln[A]_0}= (-0.0462\:min^{-1})(60\: min) = -2.8}\)
   \(\mathrm{\dfrac{[A]_t}{[A]_0} = e^{-2.8}}\)
   \(\mathrm{[A]_t = [A]_0 e^{-2.8}}\)
   \(\mathrm{[A]_t = (2.4\:g)(e^{-2.8}) = 0.146\:g\: A}\)

Q24.21A

In a first order reaction, 95% of the original amount of reactant decomposes in 122 minutes. What is the half-life of this reaction?

S24.21A

In order to determine the half-life of the first-order reaction, we first need to determine the rate constant, \(\ce{k}\). \(\mathrm{[Reactant]_t=0.05}\) if \(\mathrm{[Reactant]_0=1.00}\) since only 5% of the original reactant remains after 122 minutes.

\(\mathrm{\ln \dfrac{[Reactant]_t}{[Reactant]_0}=-kt=\ln\dfrac{0.05}{1}=-2.996=-k(122\,min)}\)

\(\mathrm{k=\dfrac{-2.996}{-122\,min}=0.024555\,min^{-1}}\)

\(\mathrm{t_{1/2}=\dfrac{0.693}{k}=\dfrac{0.693}{0.024555\,min^{-1}}=28.2\,min}\)

Q24.21B

\(\mathrm{A \rightarrow products}\) is a first order reaction. 97% of reactants decompose in 137 minutes. What is the half-life, t_1/2, of this decomposition?

S24.21B

For more help see: Half-lives and Pharmacokinetics

\(\mathrm{0.03 = \dfrac{[A]_t}{[A]_0} = e^{-kt}}\)

\(\mathrm{\ln (0.03) = \ln e^{-kt}}\)

\(\mathrm{\ln (0.03) = - kt}\)

\(\mathrm{\ln (0.03) = - k (137\, minutes)}\)

\(\mathrm{= \dfrac{\ln 2}{-0.0255}}\)

Q24.21C

In the first order reaction \(\mathrm{D \rightarrow products}\) it is found that 90% of the original amount of reactant \(\ce{D}\) decomposes in 140 minutes. Find the half life of the decomposition reaction.

S24.21C

Use the equation. \(\mathrm{\dfrac{\ln[A]_t}{\ln[A]_0} = -kt}\)

\(\mathrm{100\%-90\% = 10\%\: left}\)

\(\mathrm{\dfrac{\ln[0.1]}{1.00} = -k(140\: min)}\) \(\mathrm{k = 0.0164\: min^{-1}}\)

\(\mathrm{Half\: life = \dfrac{\ln (2)}{0.0164} = 42.3\: min}\)

Q24.23A

If a first order decomposition reaction has a half-life of 107 minutes, in what amount of time will the original reactant be ¼ of its original concentration?

S24.23A

In order to determine the amount of time for this decomposition reaction to occur, we must first determine the rate constant \(\ce{k}\) by using the half-life.

\(\mathrm{t_{1/2}=\dfrac{0.693}{k}}\)

\(\mathrm{k=\dfrac{0.693}{t_{1/2}}=\dfrac{0.693}{107\,min}=0.00648\,min^{-1}}\)

\(\mathrm{\ln\dfrac{[Reactant]_t}{[Reactant]_0}=-kt=\ln\dfrac{0.25}{1}=-1.386=-0.00648\,min^{-1}t}\)

\(\mathrm{t=\dfrac{-1.386}{-0.00648\,min^{-1}}=214\,min}\)

Q24.23B

The decomposition reaction of 5g of reactant \(\ce{A}\) has a half-life of 50 minutes. Given the reaction is first order, how long will it take for reactant \(\ce{A}\) to decompose 40%?

Use the following data sets for questions 27 and 29.

Data Set 1 \(\mathrm{k= 4.56E\,\textrm{-2}}\)

Time, seconds	\(\ce{[A]}\), M
0	2.00
50	1.77
100	1.65
150	1.34
200	1.00
250	0.95
300	0.50
350	0.08

 

Data Set 2 \(\mathrm{k=5.87E\,\textrm{-2}}\)

Time, seconds	\(\ce{[A]}\), M
0	2.0
50	1.5
100	1.3
150	0.5
200	0

 

Data Set 3 \(\mathrm{k= 6.2E\,\textrm{-2}}\)

Time, seconds	\(\ce{[A]}\), M
0	2.0
50	1.8
100	0.67
150	0.57
200	0.3
250	0.2
300	0.1
350	0

S24.23B

For more help see: Half-lives and Pharmacokinetics

If 40% of reactant \(\ce{A}\) decomposes, that means that 60% of reactant \(\ce{A}\) is remaining 60% of 5g is 3g

Next we find \(\ce{k}\),

\(\mathrm{t_{1/2}= \dfrac{0.693}{k}}\)

\(\mathrm{k= 0.01386\: min^{-1}}\)

Next we solve for \(\ce{t}\),

\(\mathrm{\ln\left(\dfrac{3}{5}\right)= -(0.01386)(t)}\)

\(\mathrm{t= 36.86\: min}\)

Q24.23C

Acetoacetic acid, \(\ce{CH3COCH2COOH(aq)}\), a reagent used in organic synthesis, decomposes in acidic solution, producing acetone and carbon dioxide gas: \(\ce{CH3COCH2COOH(aq)\rightarrow CH3COCH3(aq) + CO2(g)}\)

This is a first-order decomposition with a halflife of 144 minutes.

How long with it take for a sample of acetoacetic acid to be 55% decomposed?

S24.23C

Start with the decomposed \(\mathrm{= 100\% - 55\% = 45\%}\) decomposed

\(\mathrm{\ln\dfrac{\dfrac{45}{100}[A]_0}{[A]_0} = \ln 0.45 = -kt}\)

Find the value of \(\mathrm{k \rightarrow k = \dfrac{\ln 2}{t_{1/2}} = \dfrac{\ln 2}{144\: minutes} = 0.00481\: min^{-1}}\)

Plug the \(\ce{k}\) value back in

\(\mathrm{\ln 0.45 = (-0.00481\: min^{-1})(t) }\)

\(\mathrm{t = 166\: seconds}\)

Q24.27A

Using Table A, determine whether each set is zero-order, first-order, or third-order.

Table A

I		II		III
Time, s	[Reactant], M	Time, s	[Reactant], M	Time, s	[Reactant], M
0	4.00	0	4.00	0	4.00
10	3.20	10	3.52	10	3.00
20	2.68	20	3.03	20	2.00
30	2.28	30	2.49	30	1.00
40	2.00	40	2.01	40	0.00
50	1.80	50	1.76
60	1.60	60	1.52
70	1.47	70	1.24
80	1.33	80	0.99

S24.27A

1. Data set I must be second-order because \(\mathrm{\dfrac{1}{[Reactant]_t}-\dfrac{1}{[Reactant]_0}=kt}\). For the first 40s in set I, \(\mathrm{\dfrac{1}{2.00\,M}-\dfrac{1}{4.00\,M}=0.25\,L\,mol^{-1}=k(40\,s)}\), \(\mathrm{k=0.00625\,L\,mol^{-1}\,s^{-1}}\).
   For the first 80s in set I, \(\mathrm{\dfrac{1}{1.33\,M}-\dfrac{1}{4.00\,M}=0.5\,L\,mol^{-1}=k(80\,s)}\), \(\mathrm{k=0.00625\,L\,mol^{-1}\,s^{-1}}\).
   Since both give the same rate constant, \(\ce{k}\), using the second-order kinetics equation, set I must be a second-order reaction.
2. Data set II must be first-order because the half-life is constant. The first half-life is approximately 40s because the reactant concentration goes from 4.00M to 2.01M (about half). The second half-life is also 40s because the reactant concentration goes from 2.01M to 0.99M (about half) from 40s to 80s.
3. Data set II must be zero-order because it is decomposing at a constant rate. Every single ten seconds, the reactant concentration decreases by another 1M.

Q24.27B

Which sets of data correspond to a:

1. Zero order reaction
2. First order reaction
3. Second order reaction

I		II		III
Time(s)	\(\ce{[A]}\), M	Time(s)	\(\ce{[B]}\), M	Time(s)	\(\ce{[C]}\), M
25	1	0	5	0	2.23
50	.85	25	2.5	25	1.82
75	.70	50	1.67	50	1.49
100	.55	75	1.25	75	1.21
125	.40	100	1	-	-
150	.25	-	-	-	-
200	.10	-	-	-	-

Q24.29A

With the information given in Table A, are you able to find the half-life of the first-order reaction? If so, give t_1/2.

S24.29A

Yes, we can determine the half-life of the first-order reaction of data set II.

\(\mathrm{\ln\dfrac{[Reactant]_t}{[Reactant]_0}=-kt=\ln\dfrac{2.01}{4.00}=-k(40\,s)}\), \(\mathrm{k=0.0172\,s^{-1}}\)

\(\mathrm{t_{1/2}=\dfrac{0.693}{k}=\dfrac{0.693}{0.0172\,s^{-1}}=40.3\,s}\)

Q24.33A

The reaction \(\ce{A + B \rightarrow C + D}\) is second order in \(\ce{A}\) and zero order in \(\ce{B}\). The value of \(\ce{k}\) is 0.0107 M^-1 min^-1. What is the rate of this reaction when \(\mathrm{[A] = 0.106\, M}\) and \(\mathrm{[B] = 3.73\, M}\)?

Q24.33B

The reaction \(\ce{W + X \rightarrow Y + Z}\) is zero order in \(\ce{X}\) and second order in \(\ce{W}\). The rate constant, \(\ce{k}\), is found to be 0.0115 M^-1min^-1. What is the rate of the reaction when \(\mathrm{[W]=0.095\,M}\) and \(\mathrm{[X]=2.67\,M}\)?

S24.33B

Using the rate equation, \(\mathrm{Rate=k[W]^2[X]^0=(0.0115\,M^{-1}min^{-1})(0.095\,M)^2(2.67\,M)^0=0.00109\,M/min}\).

Q33C

The reaction \(\ce{A + B \rightarrow C + D}\) is a first order in \(\ce{A}\) and first order in \(\ce{B}\). \(\ce{K}\) is equal to 0.0234 M^-1min^-1. What is the rate of this reaction when \(\mathrm{[A]=0.245\,M}\) and \(\mathrm{[B]=4.45\,M}\)?

S24.33C

For more help see: Half-lives and Pharmacokinetics

\(\begin{align}
\mathrm R &= \mathrm{k[A][B]}\\
&= \mathrm{(0.0234\,M^{-1}\, min^{-1})(0.245\,M)(4.45\,M)}\\
&= \mathrm{0.0255\,M\, min^{-1}}
\end{align}\)

Q24.33D

The reaction \(\mathrm{A + B \rightarrow C + D}\) is second order and first order with respect to \(\ce{B}\). The value of \(\ce{k}\) is .0351 M^-1min^-1. What is the rate of this reaction when \(\mathrm{[A] = 0.120\, M}\) and \(\mathrm{[B] = 4.6\,M}\)?

S24.33D

Simply substitute in the values for the rate equation to get the rate of reaction:

\(\mathrm{Rate = k[A]^2[B] = (0.0351\, M^{-1}min^{-1})[0.12]^2[4.6] = 0.0023\, M/min}\)

Q24.34A

A reaction 50% complete in 40.0 min. How long is the start will the reaction by 75% complete if it is (a) first order (b) zero order?

Q24.35A

The decomposition of \(\mathrm{HI\,(g)}\) at 500K is followed for 00s, yielding the following data; at \(\mathrm{t = 0}\), \(\mathrm{[HI] = 1.00\, M}\); at \(\mathrm{t =125\, s}\), \(\mathrm{[HI] = 0.90\,M}\); at \(\mathrm{t = 250\,s}\), \(\mathrm{[HI] = 0.81\,M}\); \(\mathrm{t = 375\,s}\), \(\mathrm{[HI] = 0.74\,M}\); at \(\mathrm{t = 500\,s}\), \(\mathrm{[HI] = 0.68\,M}\). What are the reaction order and the rate constant for the reaction:

\(\ce{HI(g) \rightarrow \dfrac{1}{2} H2(g) + \dfrac{1}{2} I2(g)}\)

Write the rate law for the reaction at 500 K.

Q35B

A decomposition reaction is observed at constant temperature for 800s, and the following data is recorded: at \(\ce{t=0}\), \(\mathrm{[Reactant]=2.00\,M}\); at \(\ce{t=200\,s}\), \(\mathrm{[Reactant]=1.80\,M}\); at \(\ce{t=400\,s}\), \(\mathrm{[Reactant]=1.62\,M}\); at \(\ce{t=600\,s}\), \(\mathrm{[Reactant]=1.48\,M}\); at \(\ce{t=800\,s}\), \(\mathrm{[Reactant]=1.36\,M}\). Please provide the reaction order, rate constant, and the rate law for this reaction at this temperature.

S24.35B

This reaction is of second-order because a plot of \(\ce{\dfrac{1}{[Reactant]}}\) vs. \(\ce{t}\) gives a straight line.

Time (s)	[Reactant] (M)	\(\ce{\dfrac{1}{[Reactant]}}\) (M^-1)
0	2.00	0.500
200	1.80	0.556
400	1.62	0.617
600	1.48	0.676
800	1.36	0.735

The rate constant, \(\ce{k}\), is given by the slope of this straight line.

\(\mathrm{k\approx \dfrac{0.617\,M^{-1}-0.500\,M^{-1}}{400\,s-0\,s}\approx 2.925E\,\textrm{-4}M^{-1}s^{-1}}\).

\(\mathrm{Rate=k[Reactant]^2}\).

Q35C

A common decomposition reaction is observed at constant temperature for 600s with the following data recorded: at \(\mathrm{t=0}\), \(\mathrm{[Reactant]=2.00\,M}\); at \(\mathrm{t=200\,s}\), \(\mathrm{[Reactant]=1.80\,M}\); at \(\mathrm{t=400\,s}\), \(\mathrm{[Reactant]=1.62\,M}\); at \(\mathrm{t=600\,s}\), \(\mathrm{[Reactant]=1.48\,M}\); at \(\mathrm{t=800\,s}\), \(\mathrm{[Reactant]=1.36\,M}\). Please provide the reaction order, rate constant, and the rate law for this reaction at this temperature.

S24.35C

For more help see:by graphing the reaction in a log vs x plot we see that it is a second order reaction.

\(\mathrm{k = \dfrac{0.617\,M^{-1}-0.500\,M^{-1}}{400\,s-0\,s} = 5.77\times10^{-3}}\)

Q24.36A

For the disproportionation of p-toluenesulfinic acid,

\(\ce{3ArSO2H \rightarrow Ar SO2SAr + ArSO3H + H2O}\)

(where \(\mathrm{Ar = \textrm{p-}CH_3C_6H_4}\)), the following data were obtained: \(\mathrm{t = 0\, min}\), \(\mathrm{[ArSO_2H] = 0.140\, M}\); \(\ce{15\, min}\), \(\ce{0.0965\, M}\); \(\ce{30\, min}\), \(\ce{0.0852\, M}\), \(\ce{45\, min}\), \(\ce{0.0740\, M}\); \(\ce{60\, min}\), \(\ce{0.0668\, M}\); \(\ce{120\, min}\), \(\ce{0.0493\, M}\); \(\ce{180\, min}\), \(\ce{0.0365\, M}\); \(\ce{300\, min}\), \(\ce{0.0196\, M}\).

1. Show that this reaction is second order
2. What is the value of the rate constant, \(\ce{k}\)?
3. At what time would \(\mathrm{[ArSO_2H] = 0.0600\,M}\)?
4. At what time would \(\mathrm{[ArSO_2H] = 0.0300\,M}\)?
5. At what time would \(\mathrm{[ArSO_2H] = 0.0150\,M}\)?

Q24.37A

For a certain decomposition reaction, the following observations have been made: at \(\mathrm{t=0\,s}\), \(\mathrm{[Reactant]=1.43\,M}\); at \(\mathrm{t=44\,s}\), \(\mathrm{[Reactant]=1.21\,M}\); at \(\mathrm{t=148\,s}\), \(\mathrm{[Reactant]=0.69\,M}\); and at \(\mathrm{t=264\,s}\), \(\mathrm{[Reactant]=0.11\,M}\). Determine the order and half-life of this reaction.

S24.37A

This reaction is of zero-order because a plot of \(\mathrm{[Reactant]}\) vs. \(\ce{t}\) gives a straight line.

The rate constant, \(\ce{k}\), is given by the slope of this straight line.

\(\mathrm{k=\dfrac{0.69\,M-1.43\,M}{148\,s-0\,s}=-0.00500\,M/s}\).

\(\mathrm{[Reactant]_t=\dfrac{[Reactant]_0}{2}=\dfrac{1.43\,M}{2}=0.715\,M}\)

\(\mathrm{t_{1/2}=\dfrac{0.715\,M}{0.00500\,M/s}=143\,s}\).

Q24.43A

Does the half-life of a reaction get longer or shorter as initial reactant concentration increases and why? Please answer for a) zero-order reactions b) second-order reactions.

S24.43A

1. \(\mathrm{t_{1/2}=\dfrac{[Reactant]_0}{2k}}\)
   In a zero-order reaction, half-life is proportional to initial reactant concentration, so the half-life of a zero-order reaction would get longer if the initial reactant concentration increased.
2. \(\mathrm{t_{1/2}=\dfrac{1}{k[Reactant]_0}}\)
   In a second-order reaction, half-life is inversely proportional to initial reactant concentration, so the half-life of a second-order reaction would get shorter if the initial reactant concentration increased.

Q24.45A

Explain why

1. A reaction rate cannot be calculated from solely the collision frequency.
2. The rate of a chemical reaction may increase dramatically with temperature, whereas the collision frequency rises a lot more slowly.
3. Introducing a catalyst to a reaction mixture can have such a significant impact on the rate of the reaction, even if the temperature is held constant.

Q24.45B

Answer the following:

1. What two factors does the rate of a reaction depend on other than the frequency of collisions?
2. Why does the rate of reaction increase dramatically with temperature?
3. What is the net effect of the addition of a catalyst?

S24.45B

1. 1) Whether or not the collisions occurring have enough energy to get over the activation energy and become products. 2) Whether or not the molecules involved in the collisions are situated properly for the reaction to occur.
2. Collision frequency does not increase dramatically with temperature; however, the percentage of molecules with enough energy to get over the activation energy and become products does.
3. The net effect of the addition of a catalyst is the decreasing of the energy barrier to products. The catalyst does so by enabling an alternative mechanism with a lower activation energy.

Q24.45C

Explain why

(a) A reaction rate cannot be calculated from the solely collision frequency.

Collision Frequency does not solely determine the rate of the reaction because in order to overcome the activation energy to react, temperature and concentrations will also dictate the rate of the reaction.

(b) The rate of a chemical reaction may increase dramatically with temperature, whereas the collision frequency rises a lot more slowly.

A rise in temperature results in higher kinetic energies in the molecules thus increasing the % chance of colliding AND reacting rather than colliding and staying inert. Having a steady collision frequency with higher kinetic energy will result in spiked rates of reactions.

(c) Introducing a catalyst to a reaction mixture can have such a significant impact on the rate of the reaction, even if the temperature is held constant.

Catalysts induce reactants to react with one another by lowering the activation energy of the chemical reaction. This can be done without any sort of flux in the enthalpy of the system.

S24.45C

Q24.46A

If even a small spark is introduced into a mixture of \(\ce{H2(g)}\) and \(\ce{O2(g)}\), a highly exothermic explosive reaction occurs. Without the spark, the mixture remains unreacted indefinitely.

1. Explain this difference in behavior.
2. Why is the nature of the reaction independent of the size of the spark?

Q24.47A

For the reversible reaction \(\ce{A + B \leftrightarrow A + B}\) the enthalpy change of the forward reaction is +11 kj/mol. The activation energy of the forward reaction is 74 kj/mol.

What is the activation energy for the reverse reaction?

Q24.47B

For a reversible reaction, the enthalpy change of the forward reaction is 37kJ/mol, and the activation energy of the forward reaction is 96kJ/mol.

1. With the information provided, are you able to determine the activation energy of the reverse reaction? If so, please determine it.
2. Provide a sketch of the potential energy vs. progress of reaction.

S24.47B

1. Yes we are able to determine the activation energy of the reverse reaction. Because the enthalpy change of the forward reaction is 37kJ/mol, the products are 37kJ/mol closer to the transition state than the reactants. The activation energy for the reverse reaction is \(\mathrm{96\,kJ/mol-37\,kJ/mol=59\,kJ/mol}\).
2. \(\mathrm{\Delta H=+37\,kJ}\)
   \(\mathrm{E_a(forward)=96\,kJ}\)
   \(\mathrm{E_a(reverse)=59\,kJ}\)

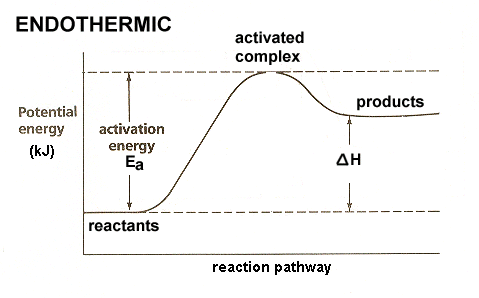
Q24.47C

For the reversible reaction \(\mathrm{A + B \leftrightarrow A + B}\) the enthalpy change of the forward reaction is +20kj/mol. The activation energy of the forward reaction is 84 kj/mol.

1. What is the activation energy of the reverse reaction?
2. Sketch the reaction plot for this reaction

Q24.48A

By an appropriate draft, indicate why there is some relationship between the enthalpy change of the activation energy for an endothermic reaction but not for the endothermic reaction.

Q24.49A

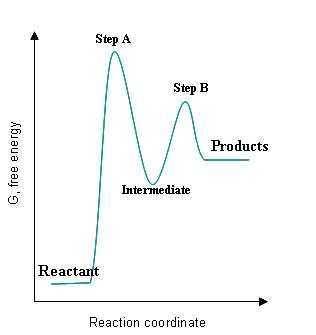
Given the following graph:

Please answer the following,

1. How can you tell where the intermediate is on the graph?
2. How can you tell where the transition state(s) is/are on the graph?
3. How can you tell where the fastest step of the reaction is on the graph?
4. How can you tell which step has the smallest rate constant?
5. How can you tell whether the steps of the reaction are exothermic or endothermic?
6. How can you tell whether the entire reaction is exothermic and endothermic?

S24.49A

1. The intermediate is a local minimum and must be brought back up to a transition state before becoming the final product(s).
2. The transition states, labeled Step A and Step B, are local maxima of the graph because they have reached the activation energy state needed to become intermediates/products.
3. The fastest step of the reaction is the one with the smallest activation energy, which in this case would be Step B because the energy gap between the intermediate and the Step B transition step is much smaller than the gap between the original reactant and the Step A transition state.
4. The smallest rate constant would correspond to the slowest reaction, which would correspond to the largest activation energy. In this case, Step A would have the smallest rate constant.
5. The steps are exothermic if their intermediates/products are lower in energy than their reactants, and the steps are endothermic if their intermediates/products are higher in energy than their reactants. Step A and Step B are endothermic because their intermediates/products are higher in energy than their reactants.
6. The overall reaction is exothermic if the initial reactant is higher in energy than the final products, and it is endothermic if the initial reactant is lower in energy than the final products. This reaction is endothermic because the reactant is lower in energy than the final products.

Q24.51A

The following observations of a reaction’s rate constant have been made: at \(\mathrm{T=325\,K}\), \(\mathrm{k=3.2E\,\textrm{-6}M^{-1}s^{-1}}\); at \(\mathrm{T=456\,K}\), \(\mathrm{k=2.8E\,\textrm{-5}M^{-1}s^{-1}}\). What is the activation energy of this reaction?

S24.51A

\(\mathrm{\ln\dfrac{k_1}{k_2}=\dfrac{E_a}{R}\left(\dfrac{1}{T_2}-\dfrac{1}{T_1}\right)=\ln\dfrac{3.2E-6M^{-1}s^{-1}}{2.8E-5M^{-1}s^{-1}}=\dfrac{E_a}{8.3145\,J\,mol^{-1}K^{-1}}\left(\dfrac{1}{456\,K}-\dfrac{1}{325\,K} \right)}\)

\(\mathrm{-2.2=-1.06\,mol\,J^{-1}(E_a)}\), \(\mathrm{E_a=2.1E4\,J\,mol^{-1}}\)

Q24.51B

The following observations of a reaction’s rate constant have been made: at \(\mathrm{T=325\,K}\), \(\mathrm{k=3.2\times10^{-6}\, M^{-1}s^{-1}}\); at \(\mathrm{T=456\,K}\), \(\mathrm{k=2.8\times10^{-5}\, M^{-1}s^{-1}}\). What is the activation energy of this reaction?

S24.51B

For more help see: Section on Ahraneous's equation

Solution: use \(\mathrm{\ln\dfrac{k_1}{k_2} = \dfrac{E_a}{R} \left(\dfrac{1}{T_2}-\dfrac{1}{T_1}\right)}\)
\(\mathrm{\ln\dfrac{2.8\times10^{-5}}{3.2\times10^{-6}} = \dfrac{E_a}{8.3145\, J/mol\, K} \left(\dfrac{1}{325}-\dfrac{1}{456}\right)}\)
\(\mathrm{-4.21 = \dfrac{E_a(-2.22 \times 10^{-4})}{8.314}}\)
\(\mathrm{-35.004 = E_a(-2.22 \times 10^{-4})}\)
\(\mathrm{E_a = 2.25 \times 10^4\: J/mol\: or\: 159\: kJ/mol}\)

Q24.51C

The rate constant for the reaction \(\ce{H2(g) + F2(g) \rightarrow 2HF}\) has been determined at the following temperatures 650 degrees k, \(\mathrm{k = 4.8 \times 10 ^{-4}\, M^{-1}s^{-1}}\); 700 degrees K, \(\mathrm{k = 3.0 \times 10^{-2}\,M^{-1}s^{-1}}\). Calculate the activation energy for the reaction.

S24.51C

Use the Arrhenius equation:

\(\mathrm{\ln\dfrac{k_1}{k_2} = \dfrac{E_a}{R} \left(\dfrac{1}{T_2} - \dfrac{1}{T_1}\right) =\ln\dfrac{4.80 \times 10^{-4}\, M^{-1}s^{-1}}{3.00 \times 10^{-2}\, M^{-1}s^{-1}} = \dfrac{E_a}{R} \left(\dfrac{1}{700 K} -\dfrac{1}{650 K}\right)}\)

\(\mathrm{(E_a)(-1.099 \times 10^{-4}) = -4.135R}\) \(\mathrm{R=8.314\: j/(mol\: k)}\)

\(\mathrm{E_a =\dfrac{(-4.135)(8.314\: J/(mol\: k))}{-1.099 \times 10^{-4}} = 313\: kj/mol}\)

Q24.59A

The following statements about catalysis are not stated completely correct. What slight changes would you make to them?

1. A catalyst is a substance that speeds up a chemical reaction but does not take part in the reaction.
2. The function of a catalyst is to lower the activation energy allowed for a chemical reaction.

Q24.59B

1. Do catalysts take part in the reaction they catalyze? Do catalysts always speed up a reaction? Explain.
2. What is the function of a catalyst?

S24.59B

1. No, catalysts do not take part in the reactions they catalyze. No, catalysts do not always speed up a reaction; some negative catalysts, called inhibitors, can slow down the rate of a reaction.
2. Catalysts main function is to provide an alternative pathway for a reaction. By changing the mechanism for a reaction, a catalyst provides a pathway with a lower activation energy, resulting in a faster reaction.

Q24.59C

The following statements about catalysis are not stated completely correct. What slight changes would you make to them?

(a) A catalyst is a substance that speeds up a chemical reaction but does not take part in the reaction.

A catalyst is a substance that speeds up a chemical reaction but does get consumed in the reaction.

(b) The function of a catalyst is to lower the activation energy allowed for a chemical reaction.

The function of a catalyst is to lower the activation energy needed for a chemical reaction.

Q24.60A

The following substrate's concentration \(\ce{[S]}\) versus time data were obtained during an enzyme-catalyzed reaction: \(\mathrm{t = 0\, min}\); \(\mathrm{[S] = 1.00\,M}\); \(\mathrm{30\, min}\), \(\mathrm{0.90\,M}\); \(\mathrm{90\, min}\), \(\mathrm{0.70\,M}\); \(\mathrm{120\, min}\), \(\mathrm{0.50\,M}\); \(\mathrm{180\, min}\), \(\mathrm{0.20\,M}\). What order is this reaction with respect to \(\ce{S}\) in the concentration

Q24.60B

The following substrates concentration [S] versus time date were obtained during an enzyme-catalyzed reaction: t = 0 min; [S] = 1.00M; 30 min, 0.90M; 90 min, 0.70M; 120 min, 0.50M; 180 min, 0.20M. What order is this reaction with respect to S in the concentratio

Q24.61A

Please answer the following about the catalytic activity of both platinum metal and enzymes:

1. Where are there active sites?
2. Are they heterogeneous or homogeneous?
3. Are they specific or nonspecific?

S24.61A

1. The active site of platinum and of enzymes are at a metal center.
2. Enzymes are usually homogeneous, meaning they are soluble in the reactant; platinum, however, is heterogeneous, meaning it cannot be dissolved in the reactant.
3. Enzymes are extremely specific to their substrates, while platinum is usually more nonspecific.

Q24.63A

What reaction conditions are necessary to produce a straight-line graph of reaction rate vs. enzyme concentration?

S24.63A

An excess of reactant (substrate) must be available.

Q24.67A

The following reaction, \(\mathrm{2W+2X \rightarrow Y+Z}\), consists of a three-step mechanism. The first step is fast, and is as follows: \(\mathrm{W+W \leftrightarrow A}\). The third step is fast as well, and is as follows: \(\mathrm{B+X \rightarrow Z}\). Comprise a three-step mechanism that conforms to \(\ce{W}\) being of second order and \(\ce{X}\) being of first order.

S24.67A

The first criterion for the reaction mechanism is that it must add up to produce the overall reaction \(\mathrm{2W+2X \rightarrow Y+Z}\). We already have two of the three steps of the mechanism, so in order to find the second step, all we need to do is subtract the first and third steps from the overall reaction.

Overall Reaction: \(\mathrm{2W+2X \rightarrow Y+Z}\)

-First Step: \(\mathrm{-(W+W \leftrightarrow A)}\)

-Third Step: \(\mathrm{-(B+X \rightarrow Z)}\)

____________________

\(\mathrm{X+A \leftrightarrow Y+B}\) for the second step.

\(\mathrm{r_2=k_2[X][A]}\)

\(\mathrm{r_f=k_f[W]^2}\)

\(\mathrm{r_r=k_r[A]}\)

At equilibrium, rate forward=rate reverse so,

\(\mathrm{k_f[W]^2=k_r[A]}\)

\(\mathrm{[A]=\dfrac{k_f}{k_r}[W]^2}\)

\(\mathrm{r=k_2\dfrac{k_f}{k_r}[W]^2[X]}\); \(\mathrm{k= k_2\dfrac{k_f}{k_r}}\)

Rate Law: \(\mathrm{r=k[W]^2[X]}\), which conforms to \(\ce{W}\) being of second order and \(\ce{X}\) being of first order.

Q24.67B

The reaction \(\mathrm{2A + 2B \leftrightarrow 2C + 2D}\) is second order in respect to \(\mathrm{[A]}\) and first order in respect to \(\mathrm{[B]}\). A three step mechanism has been proposed. The third fast step is the \(\mathrm{second\: intermediate + B \rightarrow 2C + D}\). The first step is \(\mathrm{2A \rightarrow first\: intermediate}\). Propose an entire three step mechanism to show that it conforms to experimentally determined reaction order.

S24.67B

Write out the proposed three set of reactions:

1. \(\mathrm{2A \leftrightarrow Intermediate\: 1 \quad (Fast)}\)
2. Unknown (Slow)
3. \(\mathrm{Intermediate\: 2 + B \rightarrow C + D \quad (Fast)}\)

First: Find the rate law for this reaction: \(\mathrm{Rate = k[A]^m[B]^n}\)

m=2nd order n=1st order

as a result: \(\mathrm{Rate = k[A]^2[B]^1}\)

Consider the three equations and calculate step 2:

1. \(\mathrm{2A \leftrightarrow Intermediate\: 1\quad (Fast)}\)
2. \(\mathrm{Intermediate\: 1 + B \rightarrow D + Intermediate\: 2\quad (Slow)}\)
3. \(\mathrm{Intermediate\: 2 + B \rightarrow C + D \quad (Fast)}\)

Crossing out:

1. \(\mathrm{2A \leftrightarrow }\) Intermediate 1 \(\mathrm{\quad(Fast)}\)
2. Intermediate 1 \(\mathrm{+ B \rightarrow D +}\) Intermediate 2 \(\mathrm{\quad(Slow)}\)
3. Intermediate 2 \(\mathrm{+ B \rightarrow C + D \quad(Fast)}\)

\(\mathrm{= 2A + 2B \leftrightarrow 2C + 2D }\)

Through the concepts of mechanism and reactions, we know that the rate determining step is going to be the slowest one.

The rate law of reaction 1 is \(\mathrm{Rate = k_1[A]^2}\)

The rate law of reaction 2 is \(\mathrm{Rate = k_2[B][I_1]}\)

The rate law of reaction 3 is \(\mathrm{Rate = k_3[B][I_2]}\)

We can not have intermediates in our reaction rate law

Step 1 can also be written as \(\mathrm{Rate = k_{-1}[I_1]}\)

The two reaction 1 equations are equal, set them equal to each other:

\(\mathrm{k_1[A]^2 = k_{-1}[I_1]}\)

\(\mathrm{[I_1] = \dfrac{k_1}{k_{-1}} [A]^2}\)

let \(\mathrm{\dfrac{k_1}{k_{-1}} = k}\)

\(\mathrm{[I_1] = k[A]^2}\)

Substitute this back into the rate determining step. Combine the \(\ce{k}\) value like the previous part of this problem

As a result, the rate \(\mathrm{= k[A]^2[B]}\)

note that this is the same as the original equation.

Q24.78A

Find an expression to describe the units of rate constant, \(\ce{k}\), for a reaction in terms of order of the reaction (\(\ce{n}\)) , concentration (\(\ce{M}\)), and time (\(\ce{s}\)). Then use this expression to find the units of the rate constant, \(\ce{k}\), for a zero, first, and second order reaction.

S78A

The rate equation is \(\mathrm{rate=k[Reactant]_n}\). Rate has the units of M/s, \(\mathrm{[Reactant]}\) has the units of M, so when substituting in units for the rate equation you get, \(\mathrm{M/s=(units\: of\: k)M_n}\). By rearranging this equation you get, \(\mathrm{(units\: of\: k)=\dfrac{Ms^{-1}}{M_n}=M_{1-n}s^{-1}}\).

The above expression can be extremely helpful if the rate of the reaction, n, is already given. For example: if n=0, we can solve the equation as M1-0*s^-1. This will give us the answer: M1S^-1. We can write this as mols^-1/L or M/s because there is only 1 M.

Another helpful expression that can explain how to label the units of the rate constant k correctly is: k=(concentration units)^-(w-1) x (s)^-1

I will breakdown each part of this expression. The concentration units are the units given by the problem for the reactants for example, [A] (concentration of A). These units have been given above as M, molar or mol/L. W in the expression is the Overall rate of the reaction, which can be found by adding the superscripts of the concentrations in a reaction and solved through basic math. S is the unit of time that is given in the equation. Above it is given as seconds and will always have ^-1. Sometimes time will be given as minutes, in which case it will be identified as min.^-1.

For example: If rate=k[A]^1[B]^2, then the overall rate is 1+2= 3. If we wanted to find the units of k for this equation, we would plug accordingly into the expression as follows: k=(mol/L)^-(3-1) x (s)^-1. Solving we find that k= (mol/L)^-2 x (s)^-1. This can then be written as L^2/mol^2*s.

The following units for k are always true for 0, 1st, and 2nd order reactions:

When \(\mathrm{n=0}\),

\(\mathrm{(units\: of\: k)=M_{1-0}s^{-1}=M/s}\) This zero order reaction is the exact same as the one solved in the first few sentences. If we plug in 0 for n in the expression k=M1-n*s^-1 we will find that M1-0*S^-1 or M/s for k.

When \(\mathrm{n=1}\),

\(\mathrm{(units\: of\: k)=M_{1-1}s^{-1}=s^{-1}}\) Similarly, this first order reaction can be plugged in as k=M1-1*s^-1. Since 1-1=0, the concentration units won't be shown, only the time units in seconds. So since M cancels, the units for k will be s^-1 by itself.

When \(\mathrm{n=2}\),

\(\mathrm{(units\: of\: k)=M_{1-2}s^{-1}=M^{-1}s^{-1}}\) In this second order reaction, n=2. We will plug this in as k=M1-2*s^-1. 1-2=-1 so our concentration units will be M^-1. The units for k will be M^-1*s^-1.

Q24.87A

The overall reaction \(\ce{H2 + Br2 \rightarrow 2HBr}\) occurs in the following three step mechanism:

1. \(\mathrm{Br_2 \overset{k_1}{\underset{k_{-1}}{\longleftrightarrow}} 2Br\: (forward\: and\: reverse\: reactions\: are\: fast)}\)
2. \(\mathrm{ Br+H_2 \xrightarrow{k_2} HBr+H\:(slow)}\)
3. \(\mathrm{H+Br_2 \xrightarrow{k_3} HBr+Br \:(fast)}\)

\(\mathrm{k_1=5.7E4}\) ; \(\mathrm{k_{-1}=4.5E4}\) ; \(\mathrm{k_2=2.7E\,\textrm{-1}}\) ; \(\mathrm{k_3=1.6E3}\). What is the rate constant, \(\ce{k}\) , and the rate law for the entire reaction?

S87A

Because step ii is the slow step, it is the rate determining step and the rate law should be derived according to it.

\(\mathrm{\dfrac{1}{2}\left (\dfrac{d[HBr]}{dt} \right )=k_2[Br][H_2]}\)

The ½ coefficient is needed to account for the two \(\ce{HBr}\) being made. \(\ce{[Br]}\) is an intermediate, so its rate of formation must equal its rate of decomposition:

\(\mathrm{k_1[Br_2]=k_{-1}[Br]^2}\), \(\mathrm{[Br]=\dfrac{k_1}{k_{-1}}[Br_2]^{1/2}}\)

We can now replace \(\ce{[Br]}\) in the original rate law expression, giving:

\(\mathrm{Rate=k_2\left(\dfrac{k_1}{k_{-1}}\right)^{1/2}[H_2][Br_2]^{1/2}}\)

Meaning \(\mathrm{k= k_2 \left(\dfrac{k_1}{k_{-1}}\right)^{1/2}=(2.7E-1)\left(\dfrac{5.7E4}{4.5E4}\right)^{1/2}=0.30}\)

Q24.87B

Find the general rate law and the magnitude of \(\ce{k}\) for the overall reaction.

1. \(\ce{2(N2O5 \rightarrow NO2 + NO3)}\)
2. \(\ce{NO2 \rightarrow NO3 \rightarrow NO2 + O2 + NO}\)
3. \(\ce{NO + NO3 \rightarrow 2NO2}\)

S24.87B

\(\ce{2N2O5 + NO2 + NO3 + NO + NO3 \rightarrow 2NO2 + 2NO3 + NO2 + O2 + NO + 2NO2}\)
\(\ce{\Rightarrow 2N2O5 \rightarrow 4NO2 + O2 \: (overall\: reaction)}\)

1. \(\ce{NO + Br2 \leftrightarrow NOBr2 \: [Fast,\: revers.]}\)
2. \(\ce{NOBr2 + NO \rightarrow 2NOBr \: [Slow, \: RDS]}\)

\(\mathrm{\Rightarrow Rate = Rate_2 = k_2[NO][NOBr_2]}\)
\(\mathrm{\rightarrow Rate_1 = Rate_{-1} \rightarrow k_1[NO][Br_2] = k-1[NOBr_2]}\)
\(\mathrm{\rightarrow [NOBr_2] = \dfrac{k_1}{k_{-1}}[NO][Br_2]}\)
\(\mathrm{\Rightarrow Rate = k_2[NO][NOBr_2] = k_2[NO]\dfrac{k_1}{k_{-1}}[NO][Br_2]}\)
\(\mathrm{\Rightarrow Rate = \dfrac{k_2k_1}{k_{-1}}[NO]^2[Br_2] = k[NO]^2[Br_2]}\)
\(\mathrm{\rightarrow \textrm{Experimental rate law:}\: Rate = k[NO]^2[Br_2]}\)
\(\mathrm{\rightarrow \textrm{Consistent with the exp. rate law}\: (k = \dfrac{k_2k_1}{k_{-1}})}\)