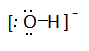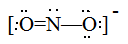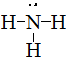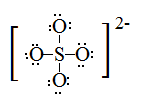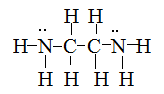21: Complex Ions & Coordination Compounds
- Page ID
- 8292
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)These are homework exercises to accompany the Textmap created for "General Chemistry: Principles and Modern Applications " by Petrucci et al. Complementary General Chemistry question banks can be found for other Textmaps and can be accessed here. In addition to these publicly available questions, access to private problems bank for use in exams and homework is available to faculty only on an individual basis; please contact Delmar Larsen for an account with access permission.
Q21.3A
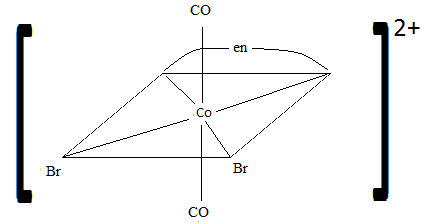
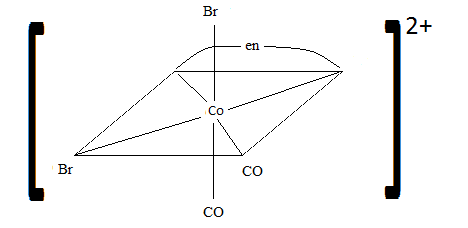
Sketch the geometric isomers of \(\ce{[CoBr2(en)(CO)2]-}\).
S21.3A
Q21.3B
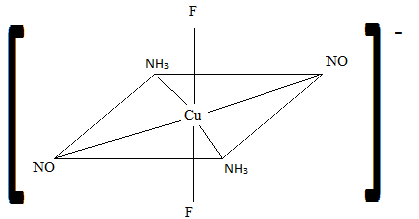
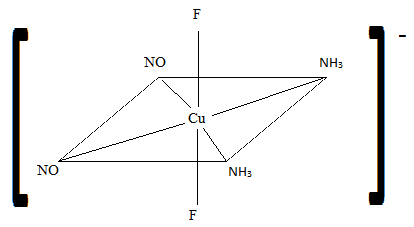
Sketch the geometric isomers of \(\ce{[CuF2(NH3)2(NO)2]-}\).
Q21.3C
Name these complex compounds:
- \(\ce{[CoCl(H2O)2(NH3)3]I2}\)
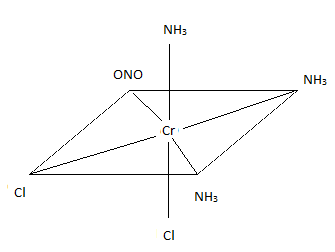
- \(\ce{[CrBr2(CO)2(NO)2]+}\)
- \(\ce{K2[Fe(CN)4]}\)
- \(\ce{[CuI2BrCO]^2-}\)
- \(\ce{[Fe(ox)Cl2(H2O)]-}\)
S21.3C
- triamminediaquachlorocobalt(III) iodide
- dibromodicarbonyldinitrosylchromium(III) ion
- potassium tetracyanoferrate(II)
- bromocarbonyldiiodocuprate(I) ion
- aquadichlorooxalatoferrate(III) ion
For review on this topic, visit the page "Nomenclature of Coordination Complexes".
Q21.3D
Write the correct names for the following:
- \(\ce{[Fe(OH)(H2O)3(NH3)2]^2+}\)
- \(\ce{[Cu(ONO)2(NH3)4]}\)
- \(\ce{[Pt(H2O)2(NH3)2][PtCl6]}\)
- \(\ce{[Fe(ox)2(H2O)(NH3)]-}\)
- \(\ce{Ag2[HgCl4]}\)
S21.3D
- diamminetetraaquahydroxoiron(III) ion
- tetraamminedinitrito-Ocopper (III)
- diamminediaquaplatinum(II) hexachloroplatinum(IV)
- ammineaquadioxalatoiron (II) ion
- silver tetrachloromercurate (II)
To review complex coordination nomenclature, visit "Naming Coordination Complexes".
Q21.3E
- Sketch the geometric isomers of \(\ce{[FeCl2(CO)2(NH3)2]}\).
- Sketch the geometric isomers of \(\ce{[NiCl4(NO)2]}\). Label whether it is cis, trans, mer, fac, or none.
Q21.4A
- How many unpaired electrons would you expect to find in the complex \(\ce{[Fe(CN)6]^3+}\)?
- How many unpaired electrons would you expect to find in the tetrahedral complex \(\ce{[MnBr4]^2-}\)? Would you expect more, fewer, or the same number of unpaired electrons as in the octahedral complex \(\ce{[Mn(NH3)6]^2+}\)?
S21.4A
- 1
- \(\ce{[MnBr4]^2-}\) would have 5 unpaired electrons. \(\ce{[Mn(NH3)6]^2+}\) has 1 unpaired electron.
For review on this topic, visit the page "High Spin and Low Spin".
Q21.4B
- How many unpaired electrons would you expect to find in the octahedral complex \(\ce{[CoF6]^3-}\)
- How many unpaired electrons would you expect to find in the tetrahedral complex \(\ce{[FeBr4]^2-}\)? Would you expect more, fewer, or the same number of unpaired electrons as in the octahedral complex \(\ce{[Co(NH3)6]^3+}\)
S21.4B
- weak field ligand so 4 unpaired electrons
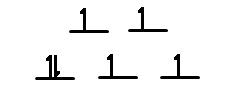
- More unpaired electrons in tetrahedral complex
For review on ligands, visit the following pages: "Ligands" and "Spectrochemical Series".
Q21.4C
- How many unpaired e- would you find in the octahedral complex \(\ce{[ZnCl6]^4-}\)?
- How many unpaired electrons would you expect to find in the tetrahedral complex \(\ce{[CuI4]^2-}\)? Would you expect more unpaired electrons in the octahedral complex \(\ce{[Mn(NH3)8]^3+}\)?
S21.4C
- \(\ce{Zn}\) has oxidation number +2, so \(\ce{Zn^2+}\) has electron configuration [Ar]3d10. There are zero unpaired electrons.
- \(\ce{Cu}\) has oxidation number +2, so \(\ce{Cu^2+}\) has electron configuration [Ar]3d9. There is one unpaired electron. \(\ce{Mn}\) has oxidation number +3, so \(\ce{Mn^3+}\) has electrong configuration [Ar]3d4. There are four unpaired electrons. Therefore, this octahedral complex has more unpaired electrons than the tetrahedral complex.
Q21.5A
- The complex ion \(\ce{[Mn(CN)4]^2-}\) is paramagnetic with 1 unpaired electron. Use the crystal field theory to explain its possible structure.
- Would you expect \(\ce{[Mn(NH3)4]^2+}\) to be diamagnetic or paramagnetic? Can you use this information about magnetic properties to help you determine whether the structure is tetrahedral or square planar?
S21.5A
- The electron configuration of \(\ce{Mn^2+}\) is [Ar]3d5. Because the complex ion is paramagnetic, there will be unpaired electrons. This compound has a coordination number of 4 so it could either be square planar or tetrahedral.
- \(\ce{Mn^2+}\): [Ar]d5; 5 electrons=paramagnetic
\(\ce{NH3}\) is a strong field; it has a large crystal field splitting, which means it has a low spin according to the spectrochemical series.
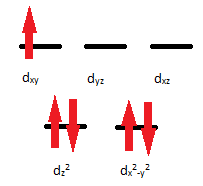
For review on this topic, visit the page "High Spin and Low Spin".
Q21.5B
- Use crystal field theory to draw the most probably structure of \(\ce{[CoF6]^3-}\) in a weak field.
- Determine whether \(\ce{[Cu(H2O)4]^2+}\) is paramagnetic or diamagnetic.
S21.5B
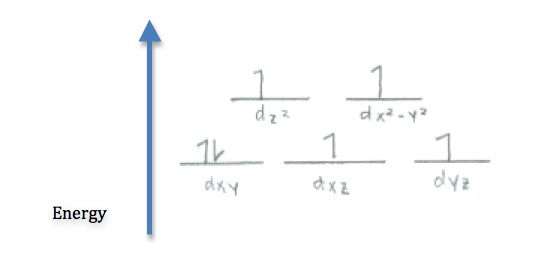
- Since \(\ce{Cu^2+}\) has 9 electrons, the only way to arrange that in 5 d orbitals is to have one unpaired electron. Therefore it is paramagnetic.
Q21.5C
Draw Lewis structures for the following ligands: a) \(\ce{OH-}\)b) \(\ce{NO2-}\) c) \(\ce{NH3}\) d) \(\ce{SO4-}\) e) \(\ce{en}\) (hint: \(\ce{C2H8N2}\))
S21.5C
Q21.5D
Draw Lewis structures for the following ligands:
- \(\ce{NH3}\)
- \(\ce{en}\)
- \(\ce{SCN-}\)
- \(\ce{NO2-}\)
S21.5D
Step 1: Find the total number of valence electrons.
Step 2: Elements up to period 4 generally follow the "Octet Rule," meaning they need 8 electrons to fill their outer shell.
Step 3: Determine the central atom. It is usually the atom with the highest valence or the least electronegative.
Step 4: Place electrons on the outside atoms first, the remaining electrons go on the central atom (creating lone pairs and/or double bonds, triple bonds, etc).

To review Lewis structures visit "Lewis Structures"
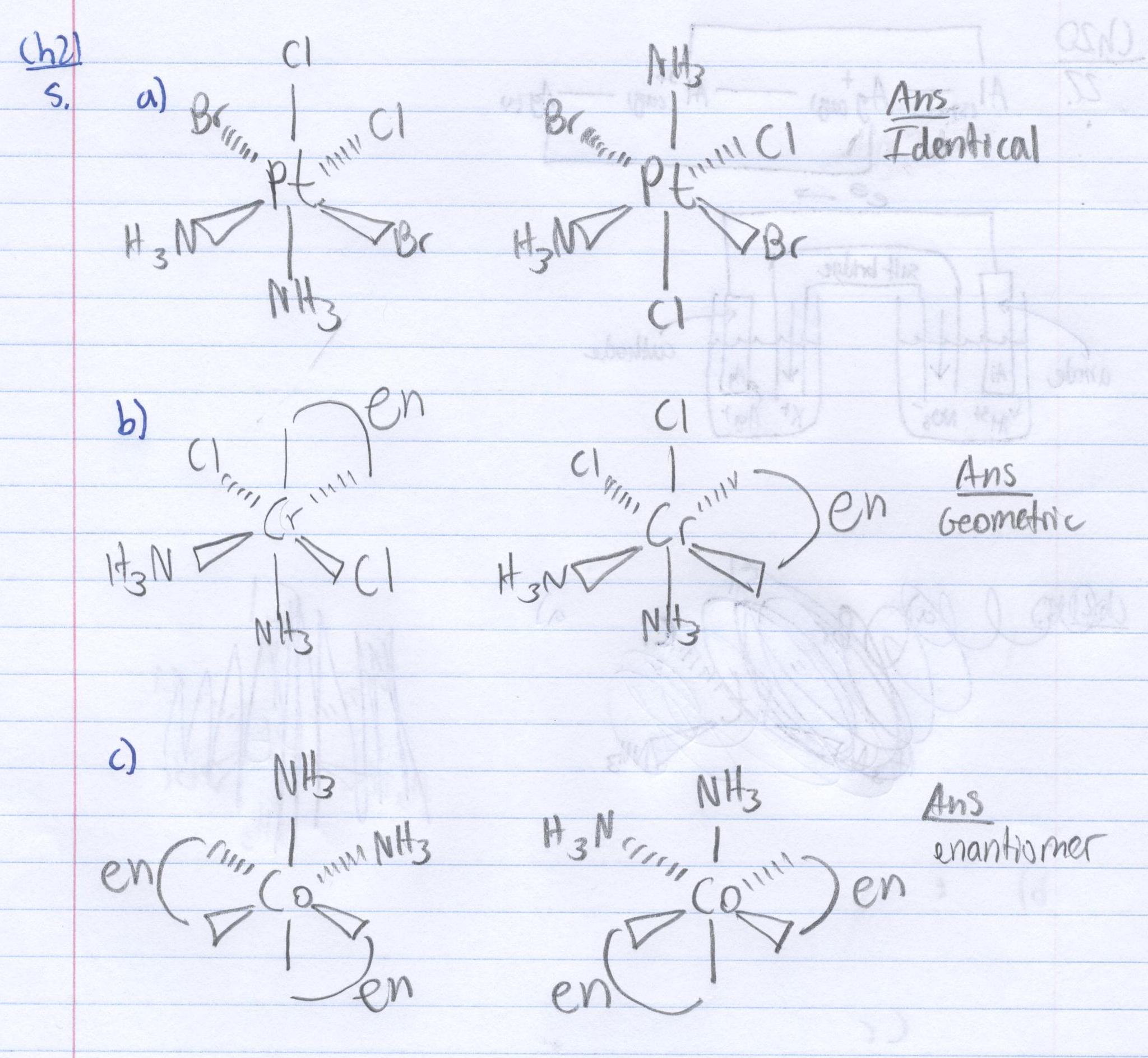
Q21.5F
Of the following complexes, name whether each pair is identical, geometric, or enantiomers.
Q21.6A
- \(\ce{[Cr(NH3)6]^3+}\) is yellow and \(\ce{[Cu(H2O)4]^2+}\) is blue. Explain why.
- One of these is blue-green and the other is yellow. Indicate which and say why. \(\ce{[Cr(H2O)6]Cl3}\) and \(\ce{[Cr(NH3)6]Cl3}\)
S21.6A
- This is because \(\ce{[Cu(H2O)4]^2+}\) absorbs yellow light and \(\ce{[Cr(NH3)6]^3+}\) absorbs blue light. They appear as the color opposite them on the color wheel.
- This is because \(\ce{NH3}\) is a stronger ligand than water so it absorbs shorter wavelengths due to the increased \(\mathrm{\Delta^\circ}\). Therefore longer wavelengths are emitted.
Q21.6C
- \(\ce{[CoF6]^3-}\)is seen as green while \(\ce{[Co(H2O)6]^3+}\) is seen as blue.
Explain the color difference. - One of the following complexes appears green and the other appears violet: \(\ce{[Cr(OH)6]^3-}\); \(\ce{[Cr(NH3)6]^3+}\). Indicate which is which, and explain.
S21.6C
- Both cobalt (III) complexes are octahedral and have an electron configuration [Ar]3d6.
In order to understand this, we must calculate the charge of Cobalt in both complexes:
For [CoF6]^3-, we know that there are 6 Fluoride according to the subscript and we know that Fluoride has a charge of -1.
We are trying to find the charge of Cobalt so we will set up an equation as:
Co+6*-1=-3 (which is the overall charge).
Through basic math we can conclude that the charge of Cobalt is +3.
Similarly, we calculate the charge for Cobalt in the complex [Co(H20)6]^3+. We can conclude that the complex has six H20 and an overall charge of +3. We can set up an equation as:
Co+6*0=+3
We can conclude that the charge is +3 for Cobalt in both complexes. Since Cobalt is #27 on the Periodic table, we subtract 3 electrons from its original 27 to get a result of 24 which is it's electron configuration. By using the nearest noble gas, Argon which is #18, we can use it to confirm Cobalt's electron configuration and writing it in a different format. Since 24-18 is 6, the number of electrons in the 3d orbital is 6. We can then write the configuration as [Ar]3d^6.
We know that H20 has a charge of 0, which can be due to it's bent shape.
Both have weak crystal field splitting, meaning that the electron orbital diagram is high spin.This also means that the Delta will be small in their diagrams.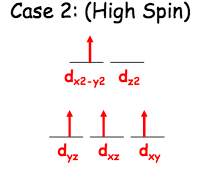 This is an example of a high spin diagram. In our example, dz2 would have one arrow and dyz would have one more arrow. In high spin cases with small deltas, we fill the bottom row before filling the top. If there are still more electrons leftover, we fill the bottom from the begining again.
This is an example of a high spin diagram. In our example, dz2 would have one arrow and dyz would have one more arrow. In high spin cases with small deltas, we fill the bottom row before filling the top. If there are still more electrons leftover, we fill the bottom from the begining again.
Although, according to the spectrochemical series, \(\ce{H2O}\) produces a greater splitting of the d energy orbital than \(\ce{F}\); therefore, \(\ce{[Co(H2O)6]^3+}\) absorbs light of a shorter wavelength while \(\ce{[CoF6]^3-}\)absorbs light of a longer wavelength. Here we see the spectrochemical series from lowest to greatest splitting of the d energy orbital. Notice the locations of H20, which is greater than F-.
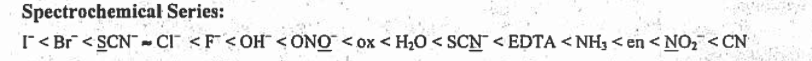
\(\ce{[Co(H2O)6]^3+}\) absorbs orange while \(\ce{[CoF6]^3-}\) absorbs red. The color that complexes appear is the complimentary or opposite color on the color wheel of the color that the complexes absorb. This is true because H20 has a higher delta and since delta is inversely proportional to lambda, wavelength, its wavelength will be the lower of the two proposed colors. This proves that H20 absorbs orange. Since F- has a lower delta, its lambda will be higher which proves that it is red, the higher wavelength. Thus, \(\ce{[CoF6]^3-}\) appears green and \(\ce{[Co(H2O)6]^3+}\)appears blue.
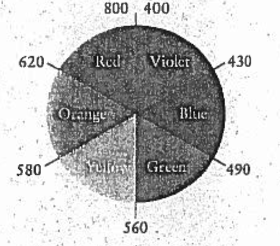 Here we can see that Green is opposite of Red and Blue is opposite of Orange.
Here we can see that Green is opposite of Red and Blue is opposite of Orange. 
- Since \(\ce{OH-}\) produces a weaker splitting of the d energy orbital than \(\ce{NH3}\) based off the spectrochemical series, \(\ce{[Cr(OH)6]^3-}\)will absorb a longer wavelength (red) and it will appear green while \(\ce{[Cr(NH3)6]^3+}\) absorbs yellow and appears violet.
www.youtube.com/watch?v=0FaAZJ2zEPk&t=3s
This link provides an example at the end of the video that can help to solve this problem if there is still any confusion. First, we must look at the spectrochemical series,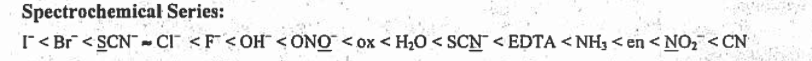
We can see that OH- is lower on the series than NH3. This means it has a lower delta and a higher lambda as we discussed before. Oppositely, NH3 has a higher delta and a lower lambda. This means that the first sentence is true. OH- will absorb the longer of the two proposed wavelengths which is red and it will appear green since green is complimentary to red on the color wheel. NH3 will absorb the shorter wavelength, yellow, and appear as it's complimentary color, violet.
For review on this topic, visit the page "Colors of Coordination Complexes".
Q21.7A
Draw:
- \(\ce{[PtI4]^2-}\)
- \(\textrm{fac-}\ce{[Cu(H2O)3(NH3)3]^2+}\)
- \(\ce{[CoCl(H2O)5]^2+}\)
Q21.7B
Draw out the following structures
- \(\ce{[PtF4]^2-}\)
- \(\textrm{Mer-}\ce{[Co(H2O)3(NH3)3]^2+}\)
- \(\ce{[FeSCN(H2O)5]^2+}\)
Q21.9A
Draw:
- pentaaquasulfatochromium (III) ion
- trioxalatoferrate (III) ion
- triamminedichloronitrito-o-chromium (III)
Q21.9B
Draw the following structures.
- pentamminechlorocobalt(III)ion
- dioxalatonickel(II) ion
- diamminetrichloronitrito-N-chromium(III) ion
Q21.11A
Explain which of these general structures have cis or trans isomerism: a) tetrahedral b) square planar c) linear.
S21.11A
- Tetrahedral have no geometric isomers. Geometric isomers are defined as metal complexes that differ in which ligands are adjacent to one another (cis) or directly across from one another (trans). Since tetrahedral molecules have only 109.5 bond angles between the four ligands, there is only one orientation that the ligands can bond to the metal.
- Square planar complexes can be either cis or trans, because they form bond angles at 180 and 90 degrees. Because of this, two pairs of ligands can be adjacent (cis) to each other or directly across from one another (trans). A square planar molecule can never be cis and trans at the same time, because the coordination number is 4.
- Since linear complexes only have a 180 degree bond angle, it cannot have cis or trans isomers. There is only one possible way to bond the two ligands to the metal in the coordination complex.
For review on this topic, visit the page "Stereoisomers".
Q21.11B
Which of these general structures for a complex ion would you expect to exhibit fac and mer isomerism? Explain.
- tetrahedral
- square-planar
- octahedral
S21.11B
Fac and mer isomerism can only occur in complex ions with structures that are octahedral in structure. These isomers involve the orientation of three ligands on the ion. Three ligands can be on the same side (or face) and be a fac isomer. Or they can be spread out across the meridian and be a mer isomer. Either way, only octahedral complexes have six ligands and therefore can sport fac and mer isomers. Answer is therefore c) octahedral.
Q21.13A
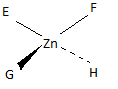
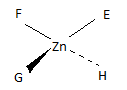
If E, F, G, H are four different ligands,
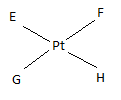
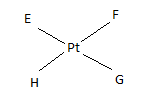
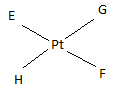
- how many geometric isomers will be found for square planar \(\ce{[PtEFGH]^2+}\)?
- will tetrahedral \(\ce{[ZnEFGH]^2+}\) display optical isomerism?
Q21.13B
If \(\ce{A}\), \(\ce{B}\), \(\ce{C}\), \(\ce{D}\) are four different ligands:
- How many geometric isomers will be found for square-planar \(\ce{[FeABCD]^2+}\)?
- Will tetrahedral \(\ce{[CuABCD]^2+}\) display optical isomerism?
Q21.15A
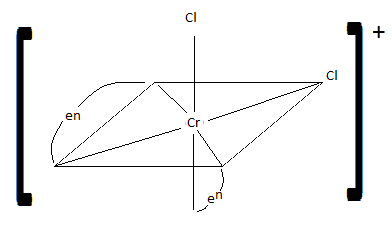
Draw cis-dichlorobis(en)chromium (III) ion. Is it chiral? Is the trans isomer chiral?
S21.15A
cis: chiral trans: not chiral
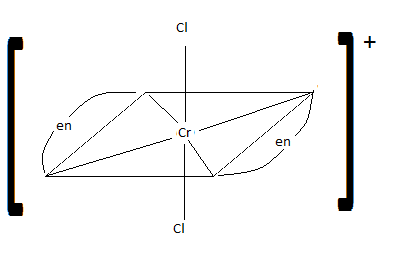
Q21.15B
Draw a structure for trans-dichlorobis(ethylenediamine)cobalt(III)ion. What kind of an isomer (geometric or optical) is the cis-dichlorobis(ethylenediamine)cobalt(III)ion.
S21.15B
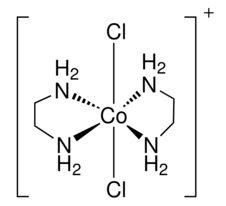
the trans-dischlorobis(ethylenediamine)cobalt(III)ion
cis-dichlorobis(ethylenediamine)cobalt(III)ion is a geometric isomer.
For review on ligands and naming of complexes visit "Ligands" and "Nomenclature of Coordination Complexes" and for review on isomers, visit "Geometric Isomers"
Q21.17A
How does crystal field theory explain the coloration of so many transition metals?
S21.17A
The Crystal Field Theory is a bonding theory used in describing the characteristic colors and magnetic properties of complex ions due to the repulsions between the negatively charged d electrons of the central metal atom and the negatively charged electrons in the ligands. Depending on the magnitude of the repulsion, the degenerate (same energy) d orbitals can either be raised to a higher energy level or dropped to a lower energy level both with respect to the average energy of the d orbitals in a ligand field. This energy, known as delta, \(\mathrm{\Delta}\), corresponds to a specific wavelength of a photon, \(\mathrm{\lambda}\), in the following equation \(\mathrm{\Delta = \dfrac{hc}{\lambda}}\). The wavelength of the photon relates to a specific color absorbed. The complementary color to the absorbed color is reflected and is the color we see. Many transition metals are colored because they have d electrons that can “jump” up to higher energy levels.
However, if there are no electrons to move up to the next energy level (as in d0compounds) or if there are no spaces to move up electrons (as in d10compounds) then there is no \(\mathrm{\Delta}\) and therefore no corresponding \(\mathrm{\lambda}\). Thus, the compound is colorless.
For review on this topic, visit the following pages "Crystal Field Theory" and "Colors of Coordination Complexes".
Q21.17B
Explain how the crystal field theory explains the different color of transition metal compounds.
S21.17B
The crystal field theory describes the interaction between the ligands and the d and central atom electrons. Due to their repulsion and attraction different ligands produce a different splitting in the d orbitals. The change in energy levels due to the splitting is the energy the complex absorbs which can correlate to the wavelength of light. From Planck’s constant we know that \(\mathrm{E=h\nu}\).
Using the speed of light \(\ce{c}\) we know that \(\mathrm{c=\lambda\nu}\) where \(\mathrm{\lambda}\) is the wavelength and \(\mathrm{\nu}\) is the frequency. We can solve for \(\mathrm{\nu=\dfrac{c}{\lambda}}\). Then we can plug it into our previous equation to get \(\mathrm{E=\dfrac{hc}{\lambda}}\)
From the equation we know depending on the energy we can find the correlating wavelength that is absorbed by the compound and we see the color that is opposite of the absorbed wavelength on the color wheel. For Qif a compound absorbed violet we would see yellow and if it absorbed green we would view it as red.
To review Crystal field theory, please visit "Crystal Field Theory".
Q21.17C
Explain the importance of the crystal field theory and its role in the coloring of so many transition metal compounds.
S21.17C
The fact that many coordination compounds are in the form of bright colors can attributed to Crystal Field Theory. Firstly, the d-orbitals are split into two levels, one being low energy and the other being high energy, which varies for different types of structures. When a photon of visible light is absorbed, however, electrons will become excited and move from the ground state to a higher energy level (excited state). That same energy difference between the levels will therefore be directly related to the energy of the photon and inversely related to the wavelenth (nm). This explains why a complex will appear to be the complementary color of its measured wavelength. Also, the strength of the ligand should be taken into consideration. Strong ligands such as \(\ce{CN}\) will have a larger Δ, meaning absorption of a shorter wavelength. Weak ligands are quite the opposite; they tend to have smaller Δ's, which allows them to absorb a longer wavelength.
For review on this topic, visit the page "Colors of Coordination Complexes".
Q21.19B
If the ion \(\ce{Ni^2+}\) is linked with strong-field ligands to produce an octahedral complex, the complex has one unpaired electron, but if linked with weak-field ligands, the compound has three unpaired electrons. How does one account for this?
S21.19B
Since the weak-field ligands have a weaker crystal field splitting, the amount of energy needed to put a second electron in an orbital is less than the amount of energy to put a first electron in the dz^2 or dx^2-y^2 orbitals, so those orbitals will have an electron put in them before any pairing occurs. With strong-field ligands, this is the opposite and the dxy, dxz, dyz orbitals will fill up first.
Q21.19C
If the ion \(\ce{Fe^2+}\) is in a tetrahedral complex with strong-field ligands, there are 2 unpaired electrons in the complex. Similarly, if \(\ce{Fe^2+}\) is in a complex with weak-field ligands, there are 4 unpaired electrons. Explain this variance.
S21.19C
Strong-field ligands always have higher Δ’s and are low-spin complexes. This particular trait is responsible for the wavering number of unpaired electrons above. Because they have large Δ’s, the electrons will fill the lower energy d orbital first before moving to the higher energy orbital. This trend will result in the least number of unpaired electrons, ensuring a low-spin. For the weak-field complex, the pairing energy, Δ, will be low enough that the electrons of the d orbital will be ordered in a manner that will allow them to be unpaired. This is why these ligands are high-spin.
3d6
For review on this topic, visit the page "Magnetic Properties".
Q21.25A
Write equations for the following:
- When \(\ce{NaOH(aq)}\) is added to \(\ce{Co(NO3)2(aq)}\), a rose-red precipitate forms.
- Adding \(\ce{NH3}\) makes the precipitate redissolve.
S21.25A
- \(\ce{2NaOH(aq) + CuSO4(aq) \rightarrow Co(OH)2 + 2NaNO3(aq)}\)
- \(\ce{Co(OH)2(s) + 4NH3(aq) \rightarrow Co(NH3)4^2+(aq) + 2OH- (aq)}\)
For review on the topic, visit "Chemical Reactions"