6.4: Enthalpy- Heat of Combustion
- Page ID
- 431538
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- State the first law of thermodynamics
- Define enthalpy and explain its classification as a state function
- Write and balance thermochemical equations
- Calculate enthalpy changes for various chemical reactions
- Explain Hess’s law and use it to compute reaction enthalpies
Standard enthalpy of combustion (\(ΔH_C^\circ\)) is the enthalpy change when 1 mole of a substance burns (combines vigorously with oxygen) under standard state conditions; it is sometimes called “heat of combustion.” For example, the enthalpy of combustion of ethanol, −1366.8 kJ/mol, is the amount of heat produced when one mole of ethanol undergoes complete combustion at 25 °C and 1 atmosphere pressure, yielding products also at 25 °C and 1 atm.
\[\ce{C2H5OH}(l)+\ce{3O2}(g)⟶\ce{2CO2}+\ce{3H2O}(l)\hspace{20px}ΔH_{298}^\circ=\mathrm{−1366.8\: kJ} \label{5.4.8}\]
Enthalpies of combustion for many substances have been measured; a few of these are listed in Table \(\PageIndex{1}\). Many readily available substances with large enthalpies of combustion are used as fuels. These include hydrogen; carbon as coal or charcoal; and hydrocarbons like methane, propane, and the major components of gasoline.
| Substance | Combustion Reaction | Enthalpy of Combustion \(ΔH_c^\circ \left(\mathrm{\dfrac{kJ}{mol} \:at\:25°C}\right)\) |
|---|---|---|
| carbon | \(\ce{C}(s)+\ce{O2}(g)⟶\ce{CO2}(g)\) | −393.5 |
| hydrogen | \(\ce{H2}(g)+\frac{1}{2}\ce{O2}(g)⟶\ce{H2O}(l)\) | −285.8 |
| magnesium | \(\ce{Mg}(s)+\frac{1}{2}\ce{O2}(g)⟶\ce{MgO}(s)\) | −601.6 |
| methane | \(\ce{CH4}(g)+\ce{2O2}(g)⟶\ce{CO2}(g)+\ce{2H2O}(l)\) | −890.8 |
| ethanol | \(\ce{C2H5OH}(l)+\ce{3O2}(g)⟶\ce{CO2}(g)+\ce{3H2O}(l)\) | −1366.8 |
| isooctane | \(\ce{C8H18}(l)+\dfrac{25}{2}\ce{O2}(g)⟶\ce{8CO2}(g)+\ce{9H2O}(l)\) | −5461 |
| glucose | \(\ce{C6H12O6}(s)+\dfrac{6}{2}\ce{O2}(g)⟶\ce{6CO2}(g)+\ce{6H2O}(l)\) | -2813 |
As Figure \(\PageIndex{1}\) suggests, the combustion of gasoline is a highly exothermic process. Let us determine the approximate amount of heat produced by burning 1.00 L of gasoline, assuming the enthalpy of combustion of gasoline is the same as that of isooctane, a common component of gasoline. The density of isooctane is 0.692 g/mL.

Solution
Starting with a known amount (1.00 L of isooctane), we can perform conversions between units until we arrive at the desired amount of heat or energy. The enthalpy of combustion of isooctane provides one of the necessary conversions. Table \(\PageIndex{1}\) gives this value as −5460 kJ per 1 mole of isooctane (C8H18).
Using these data,
The combustion of 1.00 L of isooctane produces 33,100 kJ of heat. (This amount of energy is enough to melt 99.2 kg, or about 218 lbs, of ice.)
Note: If you do this calculation one step at a time, you would find:
\(\begin {align*}
&\mathrm{1.00\:L\:\ce{C8H18}⟶1.00×10^3\:mL\:\ce{C8H18}}\\
&\mathrm{1.00×10^3\:mL\:\ce{C8H18}⟶692\:g\:\ce{C8H18}}\\
&\mathrm{692\:g\:\ce{C8H18}⟶6.07\:mol\:\ce{C8H18}}\\
&\mathrm{692\:g\:\ce{C8H18}⟶−3.31×10^4\:kJ}
\end {align*}\)
How much heat is produced by the combustion of 125 g of acetylene?
- Answer
-
6.25 × 103 kJ
How much heat is produced by the combustion of 125 g of glucose?
- Answer
-
1.95 × 103 kJ
As reserves of fossil fuels diminish and become more costly to extract, the search is ongoing for replacement fuel sources for the future. Among the most promising biofuels are those derived from algae (Figure \(\PageIndex{2}\)). The species of algae used are nontoxic, biodegradable, and among the world’s fastest growing organisms. About 50% of algal weight is oil, which can be readily converted into fuel such as biodiesel. Algae can yield 26,000 gallons of biofuel per hectare—much more energy per acre than other crops. Some strains of algae can flourish in brackish water that is not usable for growing other crops. Algae can produce biodiesel, biogasoline, ethanol, butanol, methane, and even jet fuel.

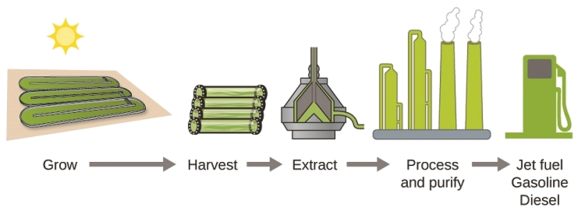
According to the US Department of Energy, only 39,000 square kilometers (about 0.4% of the land mass of the US or less than \(\dfrac{1}{7}\) of the area used to grow corn) can produce enough algal fuel to replace all the petroleum-based fuel used in the US. The cost of algal fuels is becoming more competitive—for instance, the US Air Force is producing jet fuel from algae at a total cost of under $5 per gallon. The process used to produce algal fuel is as follows: grow the algae (which use sunlight as their energy source and CO2 as a raw material); harvest the algae; extract the fuel compounds (or precursor compounds); process as necessary (e.g., perform a transesterification reaction to make biodiesel); purify; and distribute (Figure \(\PageIndex{3}\)).
Footnotes
- 1 For more on algal fuel, see www.theguardian.com/environme...n-fuel-problem.
Summary
If a chemical change is carried out at constant pressure and the only work done is caused by expansion or contraction, the heat produced or required for the change is called the enthalpy change with the symbol ΔH, or \(ΔH^\circ\) for reactions occurring under standard state conditions. The value of ΔH for a reaction in one direction is equal in magnitude, but opposite in sign, to ΔH for the reaction in the opposite direction, and ΔH is directly proportional to the quantity of reactants and products. Examples of enthalpy changes include enthalpy of combustion, enthalpy of fusion, enthalpy of vaporization, and standard enthalpy of formation. The standard enthalpy of formation, \(ΔH^\circ_\ce{f}\), is the enthalpy change accompanying the formation of 1 mole of a substance from the elements in their most stable states at 1 bar (standard state). Many of the processes are carried out at 298.15 K. If the enthalpies of formation are available for the reactants and products of a reaction, the enthalpy change can be calculated using Hess’s law: If a process can be written as the sum of several stepwise processes, the enthalpy change of the total process equals the sum of the enthalpy changes of the various steps.
Key Equations
- \(ΔU=q+w\)
- \(ΔH^\circ_\ce{reaction}=∑n×ΔH^\circ_\ce{f}\ce{(products)}−∑n×ΔH^\circ_\ce{f}\ce{(reactants)}\)
Footnotes
- 1 For more on algal fuel, see www.theguardian.com/environme...n-fuel-problem.
Glossary
- enthalpy (H)
- sum of a system’s internal energy and the mathematical product of its pressure and volume
- Hess’s law
- if a process can be represented as the sum of several steps, the enthalpy change of the process equals the sum of the enthalpy changes of the steps
- hydrocarbon
- compound composed only of hydrogen and carbon; the major component of fossil fuels
- standard enthalpy of combustion (\(ΔH^\circ_\ce{c}\))
- heat released when one mole of a compound undergoes complete combustion under standard conditions
Contributors and Attributions
Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).


