6.3: Enthalpy- Introduction

Learning Objectives

• State the first law of thermodynamics
• Define enthalpy and explain its classification as a state function
• Write and balance thermochemical equations
• Calculate enthalpy changes for various chemical reactions
• Explain Hess’s law and use it to compute reaction enthalpies

Thermochemistry is a branch of chemical thermodynamics, the science that deals with the relationships between heat, work, and other forms of energy in the context of chemical and physical processes. As we concentrate on thermochemistry in this chapter, we need to consider some widely used concepts of thermodynamics.

Substances act as reservoirs of energy, meaning that energy can be added to them or removed from them. Energy is stored in a substance when the kinetic energy of its atoms or molecules is raised. The greater kinetic energy may be in the form of increased translations (travel or straight-line motions), vibrations, or rotations of the atoms or molecules. When thermal energy is lost, the intensities of these motions decrease and the kinetic energy falls. The total of all possible kinds of energy present in a substance is called the internal energy (U), sometimes symbolized as E.

As a system undergoes a change, its internal energy can change, and energy can be transferred from the system to the surroundings, or from the surroundings to the system. Energy is transferred into a system when it absorbs heat (q) from the surroundings or when the surroundings do work (w) on the system. For example, energy is transferred into room-temperature metal wire if it is immersed in hot water (the wire absorbs heat from the water), or if you rapidly bend the wire back and forth (the wire becomes warmer because of the work done on it). Both processes increase the internal energy of the wire, which is reflected in an increase in the wire’s temperature. Conversely, energy is transferred out of a system when heat is lost from the system, or when the system does work on the surroundings.

The relationship between internal energy, heat, and work can be represented by the equation:

\[ΔU=q+w \]

as shown in Figure \(\PageIndex{1}\). This is one version of the first law of thermodynamics, and it shows that the internal energy of a system changes through heat flow into or out of the system (positive q is heat flow in; negative q is heat flow out) or work done on or by the system. The work, w, is positive if it is done on the system and negative if it is done by the system.

 

 

Figure \(\PageIndex{1}\): The internal energy, U, of a system can be changed by heat flow and work. If heat flows into the system, q_in, or work is done on the system, w_on, its internal energy increases, ΔU > 0. If heat flows out of the system, q_out, or work is done by the system, w_by, its internal energy decreases, ΔU < 0.

A type of work called expansion work (or pressure-volume work) occurs when a system pushes back the surroundings against a restraining pressure, or when the surroundings compress the system. An example of this occurs during the operation of an internal combustion engine. The reaction of gasoline and oxygen is exothermic. Some of this energy is given off as heat, and some does work pushing the piston in the cylinder. The substances involved in the reaction are the system, and the engine and the rest of the universe are the surroundings. The system loses energy by both heating and doing work on the surroundings, and its internal energy decreases. (The engine is able to keep the car moving because this process is repeated many times per second while the engine is running.) We will consider how to determine the amount of work involved in a chemical or physical change in the chapter on thermodynamics.

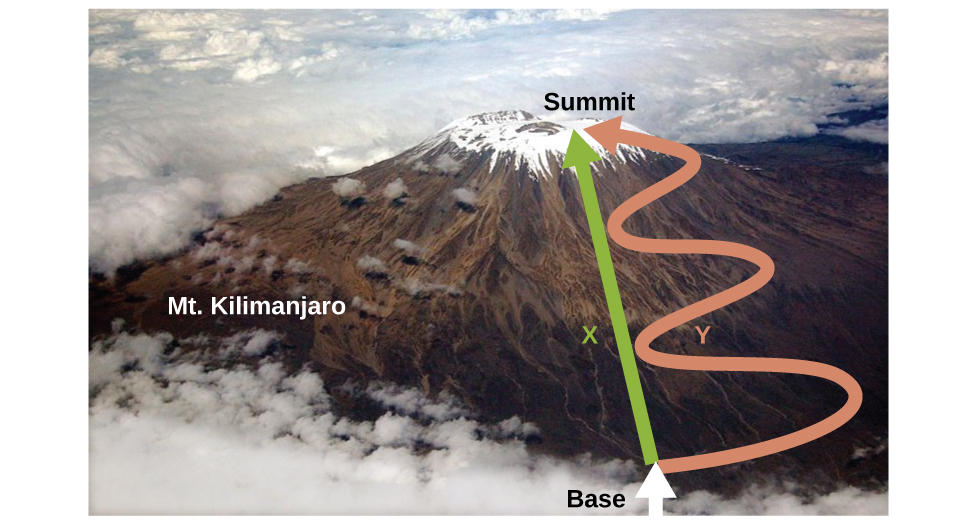
As discussed, the relationship between internal energy, heat, and work can be represented as ΔU = q + w. Internal energy is a type of quantity known as a state function (or state variable), whereas heat and work are not state functions. The value of a state function depends only on the state that a system is in, and not on how that state is reached. If a quantity is not a state function, then its value does depend on how the state is reached. An example of a state function is altitude or elevation. If you stand on the summit of Mt. Kilimanjaro, you are at an altitude of 5895 m, and it does not matter whether you hiked there or parachuted there. The distance you traveled to the top of Kilimanjaro, however, is not a state function. You could climb to the summit by a direct route or by a more roundabout, circuitous path (Figure \(\PageIndex{2}\)). The distances traveled would differ (distance is not a state function) but the elevation reached would be the same (altitude is a state function).

Figure \(\PageIndex{2}\): Paths X and Y represent two different routes to the summit of Mt. Kilimanjaro. Both have the same change in elevation (altitude or elevation on a mountain is a state function; it does not depend on path), but they have very different distances traveled (distance walked is not a state function; it depends on the path). (credit: modification of work by Paul Shaffner)

Enthalpy

Chemists ordinarily use a property known as enthalpy (\(H\)) to describe the thermodynamics of chemical and physical processes. Enthalpy is defined as the sum of a system’s internal energy (\(U\)) and the mathematical product of its pressure (\(P\)) and volume (\(V\)):

\[H=U+PV \]

Since it is derived from three state functions (\(U\), \(P\), and \(V\)), enthalpy is also a state function. Enthalpy values for specific substances cannot be measured directly; only enthalpy changes for chemical or physical processes can be determined. For processes that take place at constant pressure (a common condition for many chemical and physical changes), the enthalpy change (\(ΔH\)) is:

\[ΔH=ΔU+PΔV \]

The mathematical product \(PΔV\) represents work (\(w\)), namely, expansion or pressure-volume work as noted. By their definitions, the arithmetic signs of ΔV and w will always be opposite:

\[PΔV=−w  \]

Combining these equations yields:

\[ \begin{align} ΔH&=ΔU+PΔV \\[4pt] &=q_\ce{p}+\cancel{w}−\cancel{w} \\[4pt] &=q_\ce{p} \end{align}\]

where \(q_p\) is the heat of reaction under conditions of constant pressure.

And so, if a chemical or physical process is carried out at constant pressure with the only work done caused by expansion or contraction, then the heat flow (\(q_\ce{p}\)) and enthalpy change (\(ΔH\)) for the process are equal.

The heat given off when you operate a Bunsen burner is equal to the enthalpy change of the methane combustion reaction that takes place, since it occurs at the essentially constant pressure of the atmosphere. On the other hand, the heat produced by a reaction measured in a bomb calorimeter is not equal to \(ΔH\) because the closed, constant-volume metal container prevents expansion work from occurring. Chemists usually perform experiments under normal atmospheric conditions, at constant external pressure with \(q = ΔH\), which makes enthalpy the most convenient choice for determining heat.

Using Enthalpy

The following conventions apply when we use \(ΔH\):

1. Chemists use a thermochemical equation to represent the changes in both matter and energy. In a thermochemical equation, the enthalpy change of a reaction is shown as a ΔH value following the equation for the reaction. This \(ΔH\) value indicates the amount of heat associated with the reaction involving the number of moles of reactants and products as shown in the chemical equation. For example, consider this equation: \[\ce{H2(g) + 1/2 O2(g) ⟶ H2O (l)} \;\; ΔH=\mathrm{−286\:kJ} \label{5.4.6}\] This equation indicates that when 1 mole of hydrogen gas and 12 mole of oxygen gas at some temperature and pressure change to 1 mole of liquid water at the same temperature and pressure, 286 kJ of heat are released to the surroundings. If the coefficients of the chemical equation are multiplied by some factor, the enthalpy change must be multiplied by that same factor (ΔH is an extensive property).

\[\begin {align*} &\textrm{(two-fold increase in amounts)}\label{5.4.7}\\ &\ce{2H2}(g)+\ce{O2}(g)⟶\ce{2H2O}(l)\hspace{20px}ΔH=\mathrm{2×(−286\:kJ)=−572\:kJ}\\ &\textrm{(two-fold decrease in amounts)}\\ &\frac{1}{2}\ce{H2}(g)+\dfrac{1}{4}\ce{O2}(g)⟶\frac{1}{2}\ce{H2O}(l)\hspace{20px}ΔH=\mathrm{\frac{1}{2}×(−286\:kJ)=−143\:kJ} \end {align*}  \]

2. The enthalpy change of a reaction depends on the physical state of the reactants and products of the reaction (whether we have gases, liquids, solids, or aqueous solutions), so these must be shown. For example, when 1 mole of hydrogen gas and 12 mole of oxygen gas change to 1 mole of liquid water at the same temperature and pressure, 286 kJ of heat are released. If gaseous water forms, only 242 kJ of heat are released.

\[\ce{ H2(g) + 1/2 O2(g) ⟶ H2O(g)} \;\;\; ΔH=\ce{−242\:kJ}  \]

3. A negative value of an enthalpy change, ΔH, indicates an exothermic reaction; a positive value of ΔH indicates an endothermic reaction. If the direction of a chemical equation is reversed, the arithmetic sign of its ΔH is changed (a process that is endothermic in one direction is exothermic in the opposite direction).

Example \(\PageIndex{1}\): Measurement of an Enthalpy Change

When 0.0500 mol of HCl(aq) reacts with 0.0500 mol of NaOH(aq) to form 0.0500 mol of NaCl(aq), 2.9 kJ of heat are produced. What is ΔH, the enthalpy change, per mole of acid reacting, for the acid-base reaction run under the conditions described ?

\[\ce{HCl (aq) + NaOH(aq) \rightarrow NaCl (aq) + H2O(l)} \nonumber \]

Solution

For the reaction of 0.0500 mol acid (HCl), q = −2.9 kJ. This ratio

\[\mathrm{\dfrac{−2.9 \; kJ}{0.0500\; mol\; HCl}} \nonumber\]

can be used as a conversion factor to find the heat produced when 1 mole of HCl reacts:

\[ΔH =\mathrm{1\; \cancel{mol\; HCl} \times \dfrac{ −2.9\; kJ}{0.0500 \;\cancel{ mol\; HCl}} =−58\; kJ} \nonumber\]

The enthalpy change when 1 mole of HCl reacts is −58 kJ. Since that is the number of moles in the chemical equation, we write the thermochemical equation as:

\[\ce{HCl}_{(aq)}+\ce{NaOH}_{(aq)}⟶\ce{NaCl}_{(aq)}+\ce{H_2O}_{(l)} \;\;\; ΔH=\mathrm{−58\;kJ} \nonumber\]

Exercise \(\PageIndex{1}\)

When 1.34 g Zn(s) reacts with 60.0 mL of 0.750 M HCl(aq), 3.14 kJ of heat are produced. Determine the enthalpy change per mole of zinc reacting for the reaction:

\[ \ce{Zn}_{(s)}+\ce{2HCl}_{(aq)}⟶\ce{ZnCl}_{(aq)}+\ce{H}_{2(g)} \nonumber\]



Answer

ΔH = −153 kJ

 

\(ΔH^\circ_{combustion}\), \(ΔH^\circ_{formation}\), \(ΔH^\circ_{fusion}\), \(ΔH^\circ_{vaporization}\)

Be sure to take both stoichiometry and limiting reactants into account when determining the ΔH for a chemical reaction.

Enthalpy changes are tabulated for a variety of different processes including combustion, formation, fusion, and vaporization.  For these tabulated values the reactions are under a standard set of conditions. The IUPAC standard state is for materials at a pressure of 1 bar and solutions at a concentration of 1 M.  Many thermochemical tables list values at a pressure of 1 atm, which was previously used as the standard state.  Fortunately ΔH values do not change much with pressure and the new standard is close to 1 atm (1 bar = 0.987 atm).  The superscripted “o” in the enthalpy change symbol designates that the value is at standard conditions.

The enthalpy changes for many types of chemical and physical processes are available in the reference literature, including those for combustion reactions, phase transitions, and formation reactions. As we discuss these quantities, it is important to remember enthalpy is an extensive property - the amount of material matters.  The tabulated enthalpy values are typically listed per-mole or per-gram.  You must take this into account for any calculations.  For enthalpy calculations with chemical reactions you must also take the stoichiometry and limiting reactants into account for ΔH calculations.

Summary

If a chemical change is carried out at constant pressure and the only work done is caused by expansion or contraction, q for the change is called the enthalpy change with the symbol ΔH, or \(ΔH^\circ \) for reactions occurring under standard state conditions. The value of ΔH for a reaction in one direction is equal in magnitude, but opposite in sign, to ΔH for the reaction in the opposite direction.  And ΔH is directly proportional to the quantity of reactants and products.

Key Equations

• \(ΔU=q+w\)
• \(ΔH^\circ_\ce{reaction}=∑n×ΔH^\circ_\ce{f}\ce{(products)}−∑n×ΔH^\circ_\ce{f}\ce{(reactants)}\)

Glossary

chemical thermodynamics

area of science that deals with the relationships between heat, work, and all forms of energy associated with chemical and physical processes

enthalpy (H)

sum of a system’s internal energy and the mathematical product of its pressure and volume

enthalpy change (ΔH)

heat released or absorbed by a system under constant pressure during a chemical or physical process

expansion work (pressure-volume work)

work done as a system expands or contracts against external pressure

first law of thermodynamics

internal energy of a system changes due to heat flow in or out of the system or work done on or by the system

Hess’s law

if a process can be represented as the sum of several steps, the enthalpy change of the process equals the sum of the enthalpy changes of the steps

hydrocarbon

compound composed only of hydrogen and carbon; the major component of fossil fuels

internal energy (U)

total of all possible kinds of energy present in a substance or substances

standard enthalpy of combustion (\(ΔH^\circ_\ce{c}\))

heat released when one mole of a compound undergoes complete combustion under standard conditions

standard enthalpy of formation (\(ΔH^\circ_\ce{f}\))

enthalpy change of a chemical reaction in which 1 mole of a pure substance is formed from its elements in their most stable states under standard state conditions

standard state

set of physical conditions as accepted as common reference conditions for reporting thermodynamic properties; 1 bar of pressure, and solutions at 1 molar concentrations, usually at a temperature of 298.15 K

state function

property depending only on the state of a system, and not the path taken to reach that state

Contributors and Attributions

• Paul Flowers (University of North Carolina - Pembroke), Klaus Theopold (University of Delaware) and Richard Langley (Stephen F. Austin State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110).