13.5: Colligative Properties
- Page ID
- 44041
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction:
Colligative properties are properties of solutions, that depend on the concentration of the dissolved particles (molecules or ions), but not on the identity of those particles. They often affect solvent properties like boiling and melting point, or the vapor pressure above a fluid. There are four colligative properties we will look at:
- vapor pressure
- boiling point
- freezing point
- osmotic pressure
 Figure \(\PageIndex{1}\): Salt lowers the freezing point of water and so is used to melt ice and snow on roads. Image from Wikipedia
Figure \(\PageIndex{1}\): Salt lowers the freezing point of water and so is used to melt ice and snow on roads. Image from WikipediaVapor Pressure over a Solution
The vapor pressure over a pure liquid was covered in section 11.6 and described by the Clausius-Claperyron equation. When you add a solute to a pure liquid it becomes a solution, and what was a pure liquid is now the solvent that the solute has dissolved into. The solute will affect the vapor pressure above the solution and the effect depends on whether the solute is volatile or nonvolatile. Nonvolatile solutes depress the vapor pressure above the solution, which is only due to the solvent molecules. Volatile solutes that form miscible solutions are more complicated, as each substance has a vapor pressure, with the total vapor pressure being the sum of all the partial vapor pressures.
Nonvolatile Solutes
Nonvolatile solutes do not have an appreciable vapor pressure of their own, and they decrease the vapor pressure of a solvent (over a solution) when added to a solvent. This can be understood by the dynamics depicted in figure \(\PageIndex{2}\). In part (a) you have a pure volatile substance (solvent) and the vapor pressure (Po) is the equilibrium pressure of the solvent when the rate of evaporation equals the rate of condensation (review 11.6, Vapor Pressure as Equilibrium Pressure). Note there are 5 red lines representing the evaporating molecules and 5 black lines representing the condensing molecules (so the rate of condensation equals evaporation and the number of vapor molecules is constant). A non-volatile solute is introduced (b), and when a solute molecule is near the surface it can't escape. This effectively reduces the surface area for evaporation, and so fewer molecules transfer to the vapor phase, but those condensing have no such reduction in surface area (a vaporized solvent molecule can lose energy and condense if it his a surface solute or solvent molecule). So in (b) there are 6 black arrows entering the liquid, but only 4 red arrows leaving. The system is no longer at equilibrium and more solute condense than evaporate, reducing the vapor pressure until the ate of evaporation equals condensation and a new equilibrium has been reached (c). The result is a reduction in the vapor pressure.
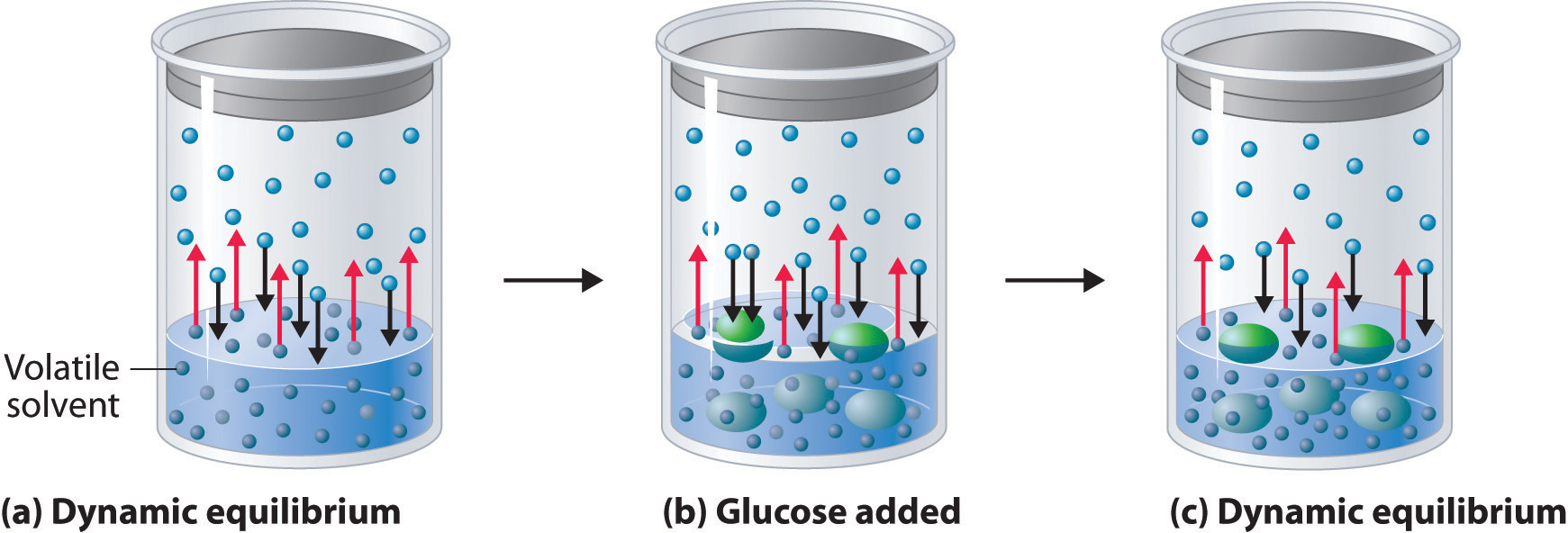 Figure \(\PageIndex{2}\): Figure showing how introducing a nonvolatile solute (glucose) to a volatile solvent (water) in a closed system reduces the rate of evaporation while not affecting the rate of condensation, resulting in a decrease in the number of vapor particles once a new dynamic equilbrium vapor pressure is achieved.
Figure \(\PageIndex{2}\): Figure showing how introducing a nonvolatile solute (glucose) to a volatile solvent (water) in a closed system reduces the rate of evaporation while not affecting the rate of condensation, resulting in a decrease in the number of vapor particles once a new dynamic equilbrium vapor pressure is achieved.
Volatile Solutes
If a volatile solute is added to a volatile solvent the total pressure is the sum of the partial pressures of both components. This is usually the case for liquid solutes like that of dissolving ethanol (alcohol) into water, where the vapor above the circuit consists of both ethanol and water molecules. If there are more than two volatile substances in a solution, the total pressure is the sum of the partial pressures of all the substances.
Raoult's Law
Raoult's Law describes the vapor pressure of a volatile substance as the mole fraction of that substance times the vapor pressure of the pure substance.
\[\underbrace{P_{substance}=X_{substance}P_{substance}^{o}}_{\text{ Vapor Pressure of a volatile substance in a solution}}\]
where,
Psubstance= vapor pressure of a volatile substance in a solution
Xsubstance= mole fraction of the volatile substance in a solution
Posubstance= vapor pressure of the pure volatile substance
Nonvolatile Solute
For a solution with a nonvolatile solute dissolved in a volatile solvent the vapor pressure is due to the solvent. This is a very simple relationship based on the fraction of particles (mole fraction) that are volatile. If a solution is half solute and half solvent on a mole basis, the vapor pressure above the solution is half that of the pure solvent. If the solution was 90% solvent on a mole basis, it's vapor pressure would be 90% of the pure solvent. In reality, most nonvolatile solutes are solids, and so can not be soluble in all proportions, that is, at some point a solution becomes saturated, and addition of further solute does not add to the solution but precipitates out.
From this we can see two expressions for Raoults law, the first one describing the vapor pressure of a volatile solvent in a solution, and the second the vapor pressure depression due to the nonvolatile solute. These two relationships are displayed by the data in figure \(\PageIndex{3}\)
- Vapor Pressure is proportional to mole fraction of solvent.
\[\underbrace{P_{solvent}=X_{solvent}P_{solvent}^{o}}_{\text{ Vapor Pressure over solution }}\]
the maximum value is that of the pure solvent
- Vapor Pressure depression is proportional to mole fraction of non-volatile solute.
\[\underbrace{\Delta P_{solvent}=-X_{solute}P_{solvent}^{o}}_{\text{ Vapor Pressure Depression due to non volatile solute}}\]
Since the solute has no vapor pressure, the depression is proportional to the fraction of the solute. Note the negative sign
 Figure \(\PageIndex{3}\): Raoult's Law plot of vapor pressure of volatile solvent with a non-volatile solute. Note this is a hypothetical system where the solute and solvent are soluble in all proportions. In reality, nonvolatile solutes are typically solids and form saturated solutions, and thus there is a limit to the possible mole fractions, which is being represented by the red dots on the graph. Only for misciple liquid/liquid solutions can the graph go from pure solute to pure solvent. Po represents the vapor pressure of the pure solvent (Xsolvent=1). The table on the right is color coded so you can see how as the mole fraction solute increases, the vapor pressure of the solvent is decreased from that of pure solvent. (CC0; Bob Belford)
Figure \(\PageIndex{3}\): Raoult's Law plot of vapor pressure of volatile solvent with a non-volatile solute. Note this is a hypothetical system where the solute and solvent are soluble in all proportions. In reality, nonvolatile solutes are typically solids and form saturated solutions, and thus there is a limit to the possible mole fractions, which is being represented by the red dots on the graph. Only for misciple liquid/liquid solutions can the graph go from pure solute to pure solvent. Po represents the vapor pressure of the pure solvent (Xsolvent=1). The table on the right is color coded so you can see how as the mole fraction solute increases, the vapor pressure of the solvent is decreased from that of pure solvent. (CC0; Bob Belford)Do not be confused by Raoult's law, it is real simple. If you have a solution that is 40% solvent and 60% nonvolatile solute, the vapor pressure is 40% of the pure solvent. If it is 90% solvent, it is 90% of the solvent. That is what Raoult's law and figure \(\PageIndex{3}\) say.
Volatile Solutes
Volatile solute are solutes that have a vapor pressure. These are typically miscible liquids that form solutions of any proportion, and so it is not always useful to distinguish one as the solvent and the other as the solute. The vapor pressure above the solution is the sum of the vapor pressure of each component within the solution (Dalton's Law of Partial Pressure, section 10.4.3)., where the vapor pressure of each component is determined by Raoult's Law. For component A, PA=XAP0A, and for component B, PB=XBP0B .We will only look at two component systems, but the vapor pressure of a system with more than two volatile solutes is simply the sum of their individual Vapor Pressures.
The vapor pressure above a solution with a volatile solute consists of vapor due to each species, and this usually occurs when miscible liquids are present, like ethanol and water, which can mix in any ration. Figure 3.4.3 shows the Raoult's Law graph of the total vapor pressure for two miscible fluids, toluene (C6H5CH3) and benzene (C6H6). Note, as you move across the graph the roles of solute and solvent switch. That is, for a solution that is 95% benzene and 5% toluene we would consider benzene to be the solvent, but we would consider toluene to be the solvent for a solution that is 95% toluene and 5% benzene.
 Figure \(\PageIndex{4}\): Vapor pressure diagram for a solution of two volatile substances. The green line shows the partial pressure of toluene, the purple line of benzene, and the red line is the sum of the two at any specified concentration.
Figure \(\PageIndex{4}\): Vapor pressure diagram for a solution of two volatile substances. The green line shows the partial pressure of toluene, the purple line of benzene, and the red line is the sum of the two at any specified concentration.The total Vapor Pressure is: PT=Xtoluene P0toluene +XbenzeneP0benzene. (Noting: Xtoluene + Xbenzene =1)
Although this looks complicated, it really is not. Each solution follows Raoult's Law where it's vapor pressure is the vapor pressure of the pure substance times the mole fraction of that substance. The total vapor pressure follows Dalton's law of partial pressures, in that the total vapor pressure is the sum of the partial pressures.
Exercise \(\PageIndex{1}\)
For a nonvolatile solute, can you derive the equation for the vapor depression dependence on the mole fraction solute (13.4.2)
\[{\Delta P_{solvent}=-X_{solute}P_{solvent}^{o}}\nonumber\]
from the equation for the vapor pressure dependence on the mole fraction solvent (13.4.1)?
\[{P_{solvent}=X_{solvent}P_{solvent}^{o}} \nonumber \]
To do this you need to recognize that
Xsolvent + X solute = 1
- Answer
-
\[\begin{align}\Delta P & =P_{Final}-P_{Initial} \nonumber \\ \nonumber \\ & =P_{solvent}^{(in\; solution)}-P_{solvent}^{0} \nonumber \\ \nonumber \\ & = X_{solvent}P_{solvent}^{0}-P_{solvent}^{0} \nonumber \\ \nonumber \\ & =P_{solvent}^{0}\left ( X_{solvent}-1 \right )\end{align}\]
Noting \(X_{solvent}+X_{solute}=1\) can be arranged to
\[X_{solute} =1-X_{solvent} \\ \text{or} \\ -X_{solute} =X_{solvent} -1\]
Substituting eq 13.4.5 into eq 13.4.4 gives eq. 13.4.2
\[\underbrace{\Delta P_{solvent}=-X_{solute}P_{solvent}^{o}}_{\text{ Vapor Pressure Depression due to non volatile solute}} \nonumber\]
Simply speaking, if a solution is 30% nonvolatile solute its pure vapor pressure depression (-\(\Delta P\)) is 0.30Posolvent, and its pressure is 70% of the pure P=0.70Posolvent. As is shown in the next exercise, you can't have all mole fraction ranges of figure 13.4.3 with a solid solute, and at some point the solution becomes saturated and a precipitate starts to form. The saturated solution represents the largest possible mole fraction of dissolved solute.
Exercise \(\PageIndex{2}\)
What is the maximum amount sucrose can depress the vapor pressure of water at 200C if the vapor pressure of pure water (Powater) is 17.5 torr and a saturated solution of sucrose has a concentration of S=\(\frac{230.9g(C_{6}H_{22}O_{11})}{100g(H_{2}O)}\) at that temperature. (Video performs solution, while describing problem).
- Answer
-
1.89 Torr
Real Solutions
There are two comments that should be made on Raoult's Law.
1. Solid solutes are usually nonvolatile, and they can not form solutions at all the concentrations described by Raoult's law, which is indicated by the dashed red line in Figure \(\PageIndex{3}\). That is, at some point a solution becomes saturated and the addition of solute causes a precipitate to form, and so you can not make solutions of all mole fractions This limitation does not happen for miscible substances, but those usually involve volatile solutes, where the total vapor pressure is the sum of the partial pressure do to all volatile species. So the equation works, but the graph can be misleading.
2. Solutions that follow Raoult's Law are considered to be Ideal Solutions, and by this we mean the solute-solvent interactions are the same as solvent-solvent. In reality, most solutions with nonvolatile solutes have stronger solute-solvent interactions than solvent-solvent, which can be considered as a reason why they are soluble. If this happens, then there are greater intermolecular forces for the solution than the pure solvent, and so there is a greater vapor pressure depression than described by Raoult's Law. This is also why there is often a contraction in volume while mixing. That is, the greater the intermolecular forces, the closer the particles are to each other, and the harder it is to vaporize them (so the vapor pressure decreases).
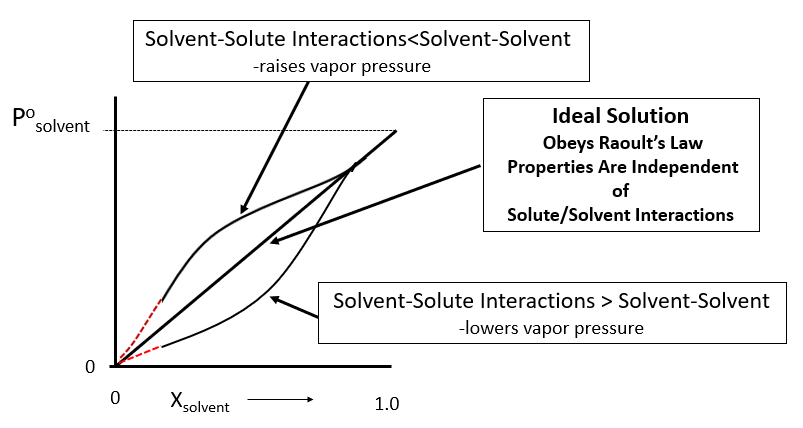 Figure \(\PageIndex{5}\): Limitations of Raoult's Law. Note, for nonvolatile solutes this deviation is usually negative and the vapor pressure depression is greater than given by Raoult's law.(Copyright; Belford CC0)
Figure \(\PageIndex{5}\): Limitations of Raoult's Law. Note, for nonvolatile solutes this deviation is usually negative and the vapor pressure depression is greater than given by Raoult's law.(Copyright; Belford CC0)Note, if the solute-solute and solvent-solvent attractions are greater than the solute-solvent, they tend not to mix, causing an insoluble solid solute, or two immiscible liquids if the solute is a liquid. But things can get complicated. For instance, acetone (CH3C(=O)CH3) and water are miscible and you can dry wet glassware by adding acetone to it. The acetone does not hydrogen bond and so has a higher vapor pressure than water, and by mixing with the water it weakens the h-bonding effect of the water, allowing the water to evaporate more easily. You need to look at figure \(\PageIndex{4}\) to understand this. Figure \(\PageIndex{5}\) as written is for a nonvolatile solute.
Boiling Point Elevation
The definition of the boiling point is the temperature at which the vapor pressure equals ambient pressure, at which point particles within the bulk of the liquid begin to vaporize. So if a non volatile solute depresses the vapor pressure, you need a higher temperature to bring the vapor pressure up to ambient, and the boiling point is elevated. This is shown in figure \(\PageIndex{6}\) where you see the vapor pressure curve for pure water, and that for an aqueous solution. If we follow the normal isobar (1 atm), the boiling point of pure water is at 100oC, when the water's vapor pressure equals 1 atm. For the solution curve, the vapor pressure is depressed (Raoult's Law), and at 100oC is less than one atm. In order to bring it up to 1 atm, the temperature is raised to about 110oC (Tb), which becomes the boiling point of the solution. This is why we often put salt in water while cooking.
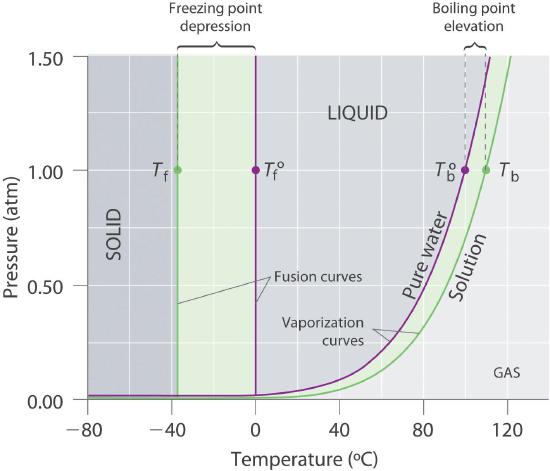
Figure \(\PageIndex{6}\): Plot showing the boiling point elevation and freezing point depression for water.
The amount the boiling point is elevated changes as the concentration of the solution changes and can be given by the following equation.
\[\underbrace{\Delta T=ik_{b}m}_{\text{ Boiling Point Elevation }}\]
Where,
\[\begin{align}i & = \text{Van't Hoff Factor} \nonumber \\ k_{b} & = \text{boiling point elevation constant} \nonumber \\ m & = \text{molality} \left ( \frac{mole_{solute}}{kg_{solvent}} \right ) \nonumber \end{align} \nonumber \]
Note: \(\Delta\)T= Tbp(solution)-Tbp(pure solvent)
Boiling Point Elevation constants can be obtained in table 13.5.2 or through the resources tab on the left of this page.
The Van't hoff factor takes into account the fact ionic compounds break up into individual ions upon dissolution, and colligative properties are an effect of the total number of particles. For covalent compounds i=1, and on a first order of approximation, the van't hoff factor of an ionic compound is equal to the number of ions within its formula
| Compound | Van't Hoff Factor (Ideal Solution) |
|---|---|
| C12H22O11 (sucrose) | 1 |
| NaCl | 2 |
| BaF2 | 3 |
| X2Y3 | 5 |
Note: Many books introduce the boiling point elevation equation in the context of nonelectrolytes where the Van't Hoff factor equals one, and then introduce it later when when the solute is an electrolytes. The values above are for "ideal solutions" where the ions of an electrolyte do not interact with each other, and these are valid for dilute solutions, but as the ion concentration increases, the ions start to interact with each other and form clusters, so the true value is less than indicated in table \(\PageIndex{1}\). This will be discussed in more detail in section 13.5.7)
BP Elevation Problems
Exercise \(\PageIndex{1}\)
Calculate the Molar Mass of Adrenaline if 0.64g is dissolved in 36.0g of CCl4 and causes a boiling point elevation of 0.49oC. Obtain kb from table 13.4.2.
- Answer
-
182 g/mol.
Exercise \(\PageIndex{2}\)
You are on a mountain at an elevation wherewater boils at 95oC and want to raise the boiling point to 100oC by adding table salt (NaCl). How much table salt do you need to add to 1 kg of water to reach 100oC?
- Answer
-
285 g NaCl
Freezing Point Depression
Freezing point depression is very similar to boiling point elevation. The freezing point is a temperature at which both a solid and liquid phase can coexist, which is a dynamic equilbrium where the rate of freezing (liquid joining the solid) is equal to the rate of melting (solid joining liquid). As seen in the video below, solute particles are only in the liquid phase, collisons of the solute with the solid do not freeze, and so they reduce the rate of freezing. But since there are no solute in the crystal, the do not affect the rate of melting. As lower temperature favors freezing, the system cools until these two processes become equal.
Video\(\PageIndex{1}\): 0.19 min YouTube animation showing how solute particles affect the process of crystalization and thus lower the freezing point.
The equation for freezing point depression is similar to that for boiling point elevation. What is important to realize is that the freezing point is depressed.
\[\begin{align}\Delta T & =ik_{f}m_{\text{ Freezing Point Depression }} \nonumber \\ & or \nonumber \\ \Delta T & =-ik_{f}m_{\text{ Freezing Point Depression }}\end{align}\]
NOTE: The freezing point is depressed (\(\Delta\)T < 0) and some tables have the value of kf as a negative number and some as a positive number, and so you have to look at the value of k to figure if you need a negative sign in the equation. (If kf is negative, use the top form of eq. 13.4.7, if kf is positive, use the bottom form of the equation (with the negative sign).
Where,
\[\begin{align}i & = \text{Van't Hoff Factor} \nonumber \\ k_{f} & = \text{freezing point point constant} \nonumber \\ m & = \text{molality} \left ( \frac{mole_{solute}}{kg_{solvent}} \right ) \nonumber \end{align} \nonumber \]
\(\Delta\)T= Tfp(solution)-Tfp(pure solvent)
NOTE: The freezing point is depressed (\(\Delta\)T < 0) and some tables have the value of kf as a negative number and some as a positive number, and so you have to look at the value of k to figure if you need a negative sign in the equation. (If kf is negative, use the top form of eq. 13.4.7, if kf is positive, use the bottom form of the equation (with the negative sign).
Boiling Point Elevation and Freezing Point Depression Constants
| Solvent | Boiling Point (°C) | Kb (°C/m) | Freezing Point (°C) | Kf (°C/m) |
|---|---|---|---|---|
| acetic acid | 117.90 | 3.22 | 16.64 | 3.63 |
| benzene | 80.09 | 2.64 | 5.49 | 5.07 |
| d-(+)-camphor | 207.4 | 4.91 | 178.8 | 37.8 |
| carbon disulfide | 46.2 | 2.42 | −112.1 | 3.74 |
| carbon tetrachloride | 76.8 | 5.02 | −22.62 | 31.4 |
| chloroform | 61.17 | 3.80 | −63.41 | 4.60 |
| nitrobenzene | 210.8 | 5.24 | 5.70 | 6.87 |
| water | 100.00 | 0.5121 | 0.00 | 1.86 |
Note, the above table gives both boiling point elevation constants and freezing point depression constants. The very next section of the chapter goes over freezing point depression.
More on van't Hoff Factor
The van't Hoff factor (i) in the freezing point depression and boiling point elevation equations is typically omitted from the equations for nonelectrolytes, and most textbooks add it on to explain that electrolytes ionize, and the true colligative effect is a result of the total number of ions in the solution. This aligns with the definition of a colligative property not depending on the identity of the solute, just the total number of particles, and we can call this an ideal solution. The actual van't Hoff factor is often less than predicted from table 13.4.1 where an ionic compound breaks up into its ions, and the van't Hoff factor is experimentally determined from the following formula:
\[i=\dfrac{\text{apparent number of particles in solution}}{\text{ number of moles of solute dissolved}} \]
| Compound | i (measured) | i (ideal) |
|---|---|---|
| glucose | 1.0 | 1.0 |
| sucrose | 1.0 | 1.0 |
| \(NaCl\) | 1.9 | 2.0 |
| \(HCl\) | 1.9 | 2.0 |
| \(MgCl_2\) | 2.7 | 3.0 |
| \(FeCl_3\) | 3.4 | 4.0 |
| \(Ca(NO_3)_2\) | 2.5 | 3.0 |
| \(AlCl_3\) | 3.2 | 4.0 |
| \(MgSO_4\) | 1.4 | 2.0 |
For an ideal solution the ions are completely independent, but in a real solution, they can start to interact with each other and form ion pairs, like in figure in the left part of table 13.4.3, which shows two ions interacting with each other, and behaving like a single particle.
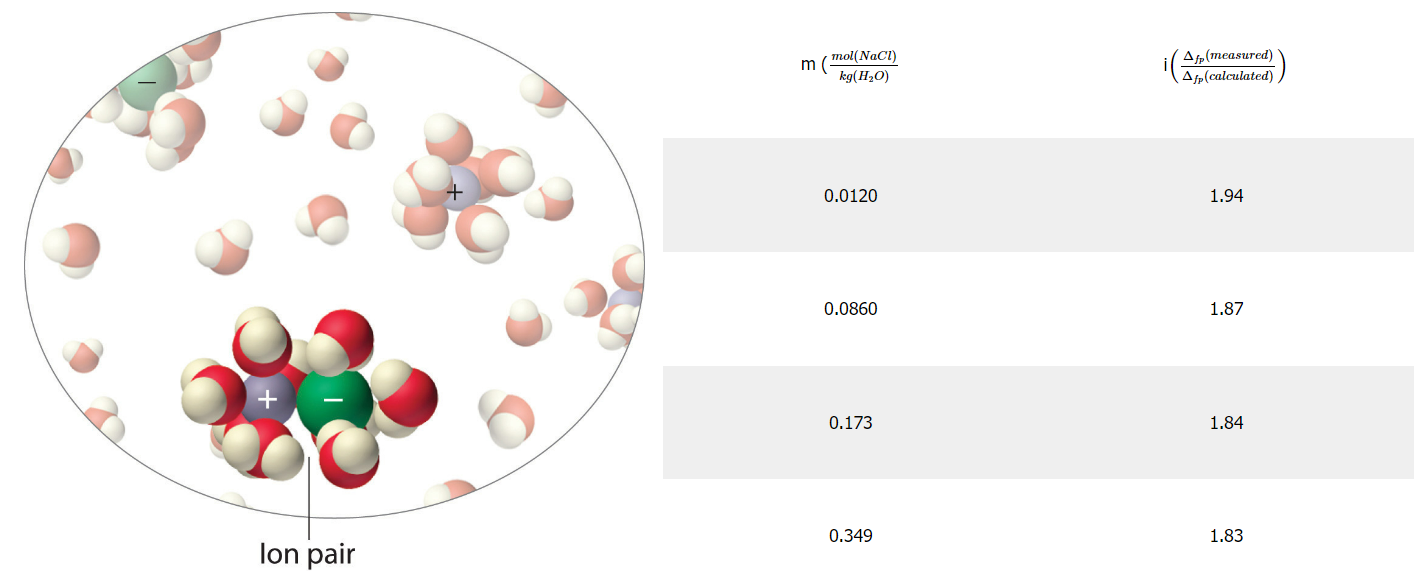 Figure \(\PageIndex{7}\): Van't Hoff factor as a function of concentration for sodium chloride. The image on the left shows to ions forming a pair, which sort of acts like a single particle. The more concentrated the solution the greater the propensity to form ion pairs and the less the ions act as discrete particles, resulting in a lowering of i from ideal conditions where every ion acts as an independent particle
Figure \(\PageIndex{7}\): Van't Hoff factor as a function of concentration for sodium chloride. The image on the left shows to ions forming a pair, which sort of acts like a single particle. The more concentrated the solution the greater the propensity to form ion pairs and the less the ions act as discrete particles, resulting in a lowering of i from ideal conditions where every ion acts as an independent particle
Osmosis
Osmosis is a colligative property where an osmotic pressure builds up across a semipermeable membrane that selectively allows solvent molecules to cross but prevents solute molecules from crossing.Osmotic pressure which can be understood through figure 13.4.7. In this image a semipermiable membrane allows water to pass, but does not allow glucose to pass. In the initial state (a) you had pure water and so the height of the two tubes are equal and then instantly add glucose to one side, this reduces the flow from right to left, and so more water enters the right side causing its height to rise to a new equilibrium. The osmotic pressure is technically defined as the pressure required to restore to bring the columns back to the same height (c), which is related to the difference in the height of the column on the right side of (b) and the left side, and the density of the solution. (\(\Pi\)=\(\rho\)gh, where \(\Pi\) is the osmotic pressure, \(\rho\) is the density, h is the difference in height of the columns and g is the gravitational constant).
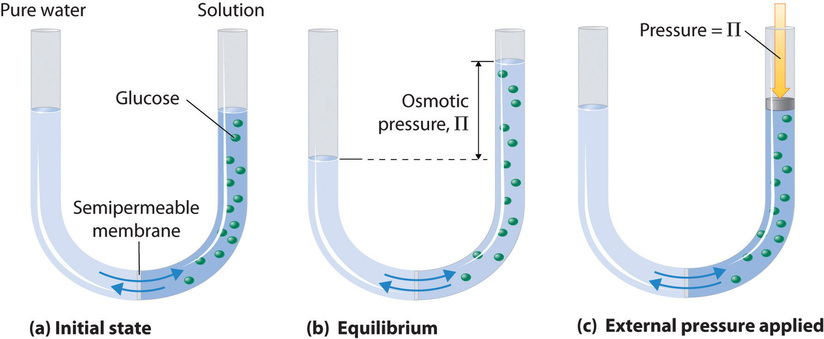
Figure \(\PageIndex{7}\):
From experimental measurements this take a form similar form to the ideal gas law,
\[\Pi V=nRT\]
which can be rearranged
\[\begin{align} \Pi & = \frac{n}{V}RT \nonumber \\ \nonumber \\ \Pi & = MRT \end{align}\]
where, M=Molarity of solute in solution, R= Ideal Gas Constant and T=absolute Temperature (Kelvin).
Exercise \(\PageIndex{2}\)
What is the osmotic pressure of a solution if you dilute 2.02 g of Urea ((NH2)2CO) at 20.0oC with water to a volume of 145mL? [Note: the answer has a YouTube Video deriving the solution].
- Answer
-
5.58 atm, see YouTube for derivation
Osmosis is very important in biology as cell membranes are semipermable. When a solution is injected into the blood it must have the same concentration as the cells or osmotic pressure can build up across them
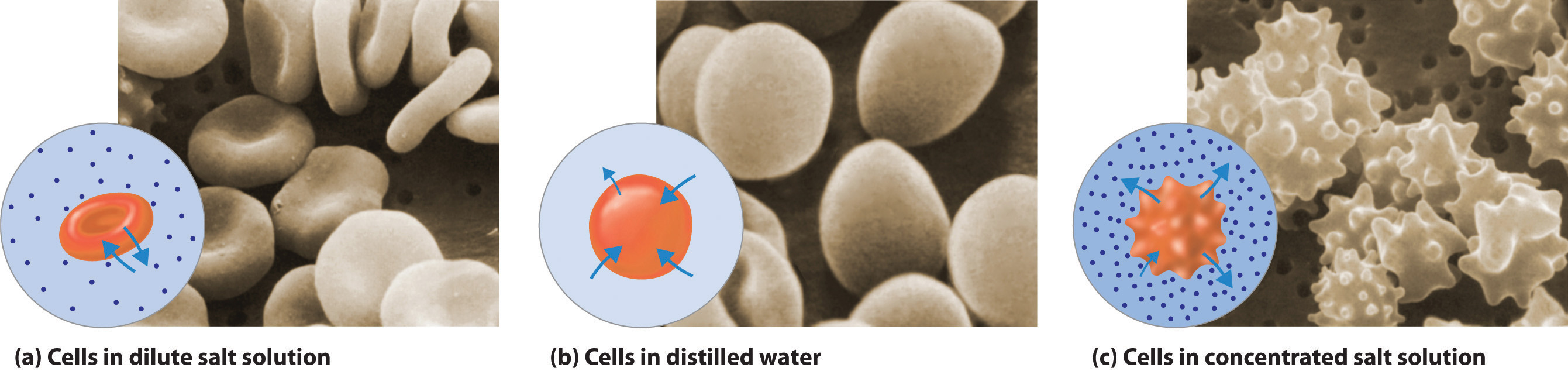
Figure \(\PageIndex{7}\): (a) Isotonic solution where the solution outside has the same concentration as a cell and the osmotic pressure is zero. In distilled water (b), which is a hypotonic fluid, the solute concentration in the cell is higher and so water flows into the cells, potentially rupturing them. In a hypertonic solution (b) the solute concentration is higher than the cell, causeing water to flow out of the cell with the result that they shrivel up.
Class Activities
ADAPT \(\PageIndex{1}\)
Test Yourself
Query \(\PageIndex{1}\)
Robert E. Belford (University of Arkansas Little Rock; Department of Chemistry). The breadth, depth and veracity of this work is the responsibility of Robert E. Belford, rebelford@ualr.edu. You should contact him if you have any concerns. This material has both original contributions, and content built upon prior contributions of the LibreTexts Community and other resources, including but not limited to:


