10.4: Gas Mixtures
- Page ID
- 52150
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Introduction
Gasses disperse throughout a container and form homogenous mixtures or solutions. Unlike liquid solutions where it is common to have a solvent that the solute actually interacts with and dissolves in, the component of a gaseous mixture are so dispersed that they essentially behave as free particles, and so there is no concept of a solute of solvent. The air that you are breathing is a mixture of gasses with 99.96% of dry air consisting of three substances; nitrogen, oxygen and argon.
| N2 | 78.08% | H2O | 0-4% | He | 5 ppm | H2 | 0.5 ppm | |||
| O2 | 20.95% | CO2 | 325 ppm | CH4 | 2 ppm | N2O | 0.3 ppm | |||
| Ar | 0.93% | Ne | 18 ppm | Kr | 1 ppm | CO | 0.05-0.2 ppm |
As each gas interacts independently of the other gasses, each gas exerts its own pressure when its particles collide with a surface, which would be known as the partial pressure of that gas.
Partial Pressure
Consider a mixture of two gasses A & B (right side of Figure \(\PageIndex{1}\), which being in the same container have the same volume and pressure. If nA is the mole of gas A and nB is the moles of gas B, we could define a partial pressure of each gas (noting that V and T are constant).
\[P_A=n_A\left ( \frac{RT}{V} \right ) \; \; \; and \; \; \; P_B=n_B\left ( \frac{RT}{V} \right )\]
where PA= partial pressure of gas A and pB = partial pressure of gas B.
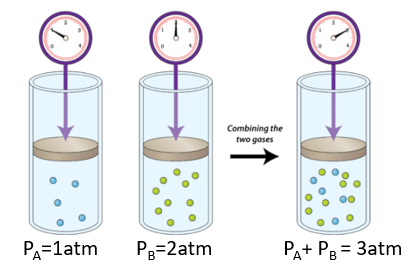
Figure \(\PageIndex{1}\): In a mixture each gas has its own partial pressure, which is the pressure that gas would exert if it was alone. Note, these cylinders are at the same volumn and temperature
If there were three gasses, the total pressure would be the sum of all three gases, and this leads to Dalton's Law of Partial Pressures.
Dalton's Law of Partial Pressure
Dalton's Law of Partial Pressures states the total pressure of a gas mixture is the sum of the partial pressures of the individual gasses
\[P_{total}=P_1+P_2+P_3 ... = \sum_i P_i\]
The Pressure of a Mixture of Gases
A 10.0-L vessel contains 2.50 × 10−3 mol of H2, 1.00 × 10−3 mol of He, and 3.00 × 10−4 mol of Ne at 35 °C.
- What are the partial pressures of each of the gases?
- What is the total pressure in atmospheres?
Solution
The gases behave independently, so the partial pressure of each gas can be determined from the ideal gas equation, using \(P=\dfrac{nRT}{V}\):
\[P_\mathrm{H_2}=\mathrm{\dfrac{(2.50×10^{−3}\:mol)(0.08206\cancel{L}atm\cancel{mol^{−1}\:K^{−1}})(308\cancel{K})}{10.0\cancel{L}}=6.32×10^{−3}\:atm}\]
\[P_\ce{He}=\mathrm{\dfrac{(1.00×10^{−3}\cancel{mol})(0.08206\cancel{L}atm\cancel{mol^{−1}\:K^{−1}})(308\cancel{K})}{10.0\cancel{L}}=2.53×10^{−3}\:atm}\]
The total pressure is given by the sum of the partial pressures:
Exercise \(\PageIndex{1}\)
A 5.73-L flask at 25 °C contains 0.0388 mol of N2, 0.147 mol of CO, and 0.0803 mol of H2. What is the total pressure in the flask in atmospheres?
- Answer
-
1.137 atm
Mole Fractions and Gas Mixtures
The mole fraction of a gas in a mixture of gasses is defined as the moles of that gas divided by moles of all gasses, for gas "A" given the symbol XA.
\[X_A=\frac{n_A}{n_T} \; \; where \; \; n_T=\sum_{i=A}^{all \; i}n_i\]
Exercise \(\PageIndex{2}\)
Using the data from table 10.4.2, determine the mole fraction of nitrogen, oxygen and argon for earth's lower atmosphere.
- Answer
-
Nitrogen = 0.7908, Oxygen = 0.2095 and Argon = 0.0093
The mole fraction can also be expressed in terms of pressure
\[X_A=\frac{P_A}{P_T}\]
which is derived in the third step of the following derivation.
Prove: \(P_A=X_AP_T\)
Solution
\[P_A = \left ( \frac{n_ART}{V} \right ) \; \; \; and \; \; \; P_T = \left ( \frac{n_TRT}{V} \right )\]
so
\[n_A=P_A\left ( \frac{V}{RT} \right ) \; \; \; and \; \; \; n_T=P_T\left ( \frac{V}{RT} \right )\]
substituting nA and nT into
\[x_A=\frac{n_A}{n_T}=\frac{P_A \cancel{\left ( \frac{V}{RT} \right )}}{P_T \cancel{\left ( \frac{V}{RT} \right )}}=\frac{P_A}{P_T}\]
rearranging gives:
\[P_A=X_AP_T\]
The following video shows how \(P_A=X_AP_T\) for a system of three gasses.
Example \(\PageIndex{1}\)
Calculate the Partial pressure if 78 g nitrogen and 42 g helium are in a pressure tank at 3.75 atm and 50.0 deg. C
Solution


