10.5: Kinetic Molecular Theory of Gases
- Page ID
- 52151
Introduction
The Kinetic Molecular Theory (KMT) describes an Ideal Gas, PV=nRT. Understanding Kinetic Molecular Theory can help us identify when a gas will behave like an ideal gas, and when it will deviate and not behave like an ideal gas.
There are five postulates to the Kinetic Molecular Theory, and gases will deviate from the ideal gas law when these postulates break down.
Five Postulates of KMT.
- Gas particles travel in straight lines unless they collide with other particles or the walls of the container.
- Gas particles have negligible volume compared to the free space between them..
- Molecular collisions are perfectly elastic and kinetic energy is conserved.
- Gas particles experience negligible intermolecular forces, there are no attractive or repulsive forces between particles.
- The average kinetic energy of the particles in a sample of gas is proportional to the absolute temperature.
The fifth postulate is very important to note as it relates kinetic energy to temperature. For a gaseous particle most of the kinetic energy is in translation.
\[E_K=\frac{1}{2}mv^2\]
But a gas is not a particle, but an ensemble of particles, all moving with different velocities in different directions. So the challenge is to describe bulk measurable properties based on the behavior of particles.
Particulate to Macroscopic Transformations
The postulates of KMT define the behavior of the particles of the gas, but the gas laws are empirical laws, in that they are derived from experimental measurements, which are not at the particulate (molecular) level. This means they are based on macroscopic observations of many molecules and not the behavior of one. A liter of oxygen is an easily measurable quantity, but how many molecules would be in a liter at STP?... and would you expect them all to have the same energy?
Exercise \(\PageIndex{1}\)
How many particles of Xenon are in 1.00 liter at STP?
- Answer
-
STP is 1 bar (0.98592 atm) at 273.15K, which is the freezing point of water, and we know that the molar volume of any ideal gas is 22.4L. So:
\[1.00L(\frac{1molXe}{22.4L})\frac{6.022x10^{23}atoms}{mol}=2.69x10^{22}atoms\; Xe\]
Yes, that was 2.693x1022 atoms in one liter! So when we describe a gas we are not describing a molecule, but an ensemble of molecules, a group of particles that is observed as the whole, not at the level of the individual molecule. This means there is a distribution of characteristics of the individual gas particle, like velocity. At any point in time some molecules are moving real fast, others slow, and some may in fact be in the middle of a collision at are not moving at all, but changing the direction that they are moving in.
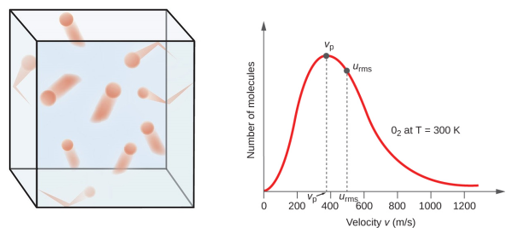
Figure \(\PageIndex{1}\): On the left is an illustration of gas particles in a container and on the right is the velocity profile for a gaseous system The discrete particles that form the gas have a range of velocities, and their distribution over the range is expressed by the area under the curve.
Typically a curve like the one in Figure \(\PageIndex{1}\) represents a macroscopically observable system in the order of a mole of particles. At any given time there is a distribution of velocities as described by the curve, and the measured values of macroscopic observables like pressure and temperature are all related to the shape of this curve, and likewise, if those values change, the shape of the curve changes.
Exercise \(\PageIndex{2}\)
What is wrong with the label of the x-axis of the velocity distribution curve in Figure \(\PageIndex{1}\)?
- Answer
-
Velocity is a vector and has direction, which means that the distribution of speeds is mapped out in 3D space (left side of Figure \(\PageIndex{1}\), and so although some gasses may be moving at 400 m/s in one direction, other molecules will be moving the same speed in the opposite direction with a cancelling out effect. Speed is the magnitude of velocity, and the x-axis really represents the distribution of the speed of the particles in the ensemble.
Although the kinetic energy of each particle in a stationary gas is 1/2mv2, we can not use the average velocity of the particles because it vectoraly adds to zero. Instead we relate its kinetic energy to the room mean square velocity, \(\mu_{rms}\).
\(\mu_{rms}\)
For a gaseous system the average kinetic energy is
\[E_{K_{ave}}=\frac{1}{2}m \mu_{rms}^2\]
Average root mean square speed for a system of n particles with individual velocities vi:
\[\mu_\ce{rms}=\sqrt{\overline{v^2}}=\sqrt{\dfrac{v^2_1+v^2_2+v^2_3+v^2_4+…}{n}}\]
Exercise \(\PageIndex{3}\)
Why do we use root mean square speed and not the arithmetic average velocity
- Answer
-
Remember velocity is a vector, and something can be moving along either the [+] or [-] directions of an axis, and for a large system of particles in random motion the number moving in the [+] or [-] is directions are roughly the same. The sum of a symmetric distribution of speeds and directions would be zero. By squaring each individual velocity all values become [+], allowing summation without cancelation, and then dividing by the total number of particles gives the average velocity square. The square root is taken to remove the effect of squaring. The resulting value is a speed (scalar) as it has a magnitude, but no direction (vector).
The important take-home message of Figure 10.5.1 is that a gas is a system of particles, each particle of which has a unique location, velocity and kinetic energy, and that we use \(\mu_{rms}^2\) to calculate the average kinetic energy of the gas (even though most of the particles actually have a different energy).
\[E_{K{ave}}=\dfrac{1}{2}mu^2_\ce{rms}\]
It can be shown that \(E_{K_{ave}}\) of a collection of gas molecules is directly proportional to the temperature of the gas and may be described by the equation:
where R is the gas constant and T is the kelvin temperature. When used in this equation, the appropriate form of the gas constant is 8.314 J mol-1K-1 (8.314 kg m2s–2mol-1K–1). These two separate equations for \(E_{K_{ave}}\) may be combined and rearranged to yield a relation between molecular speed and temperature:
\[u_\ce{rms}=\sqrt{\dfrac{3RT}{m}} \label{RMS}\]
Calculation of urms
Calculate the root-mean-square velocity for a nitrogen molecule at 30 °C.
Solution
Convert the temperature into Kelvin:
Determine the mass of a nitrogen molecule in the SI base unit of kilograms (because Joules can be expressed in the SI base units):
\[\mathrm{\dfrac{28.0\cancel{g}}{1\: mol}×\dfrac{1\: kg}{1000\cancel{g}}=0.028\:kg/mol}\]
Replace the variables and constants in the root-mean-square velocity formula (Equation \ref{RMS}), replacing Joules with the equivalent kg m2s–2:
\[ \begin{align} u_\ce{rms} &= \sqrt{\dfrac{3RT}{m}} \\ u_\ce{rms} &=\sqrt{\dfrac{3(8.314\:J/mol\: K)(303\: K)}{(0.028\:kg/mol)}} \\ &=\sqrt{2.70 \times 10^5\:m^2s^{−2}} \\ &= 519\:m/s \end{align} \]
Exercise \(\PageIndex{4}\)
Calculate the root-mean-square velocity for an oxygen molecule at –23 °C.
- Answer
-
440 m/sec
Boyle's Law & KMT (const. n,T)
At constant n and T, the velocity profile on part (b) of Figure 10.5.1 stays the same. Here we are looking at closed (constant n) isothermal (constant T) elastic system that has no resistance or heat loss to expansion or contraction.
a. Effect of \(\Delta V \) on P:
Reducing the volume of the cube in part (a) of Figure 10.5.1 increases the pressure because it increases the collision frequency of the particles with the wall. This is because they are maintaining the same velocity but have less distance to travel as they traverse the cube. Likewise, Increasing Volume decreases pressure beacuse it takes longer to traverse the expanded cube, resulting in a reduction in the collision frequency. Remember Pressure is force per unit area, and the force is the consequence of the change in momentum of the gas particle as it undergoes an elastic collision with the wall of the container (this is called an impulse in physics).
b. Effect of \(\Delta P\) on V:
Figure 10.5.2 shows this effect. Here we have a cylinder type system with a gas in a closed system. If the internal pressure is not equal to the external, the system will adjust until the are equal. Consider a system starting at state (b) where the internal volume is 3 dm3 and the pressure is 1.97 atm. If you then reduced the external pressure to 0.987 atm, the force/unit ares inside is greater than outside and the system expands until they balance and equilibrium is re-established (a). Note, in this case we cut the pressure in half, and so the volume doubled.
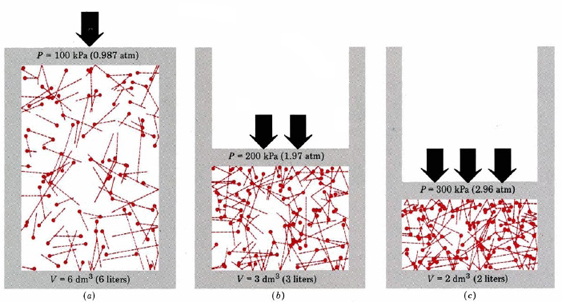
On the other hand, we could have increased the pressure of the system at (b) to 2.96 atm and now the external pressure is greater and so the system contracts until a new equilibrium is acheived (c). KMT accounts for these effects because the particles are seen to travel in straight lines until they collide with the walls of the container. Since T and n are constant, the relationship is defined by the length of the path the particles travel as they traverse the container. A larger free path (bigger V) means they collide less with the wall and so P goes down. A smaller free path means the collide with the wall more frequently, and so P goes up.
Charles Law (constant n,P)
This describes a closed elastic isobaric system that can freely expand and contract. Figure 10.5.3 shows how heating a system affects the velocity profile. Note, since n (number of molecules) is constant the area under each curve is the same. At higher temperatures the curves flatten out and move to the right, increasing urms and thus the average kinetic energy. This has two effects, first, collision frequency goes up because the the faster moving particles traverse the container quicker, and second, each collision has more energy because the particle is moving faster (EK=1/2mv2). Since the pressure (force per unit area) is being maintained constant, the area must go up to offset the increased force, and so the container expands as T goes up.

Can you cool the curve to absolute zero?
No, at some point you reach the boiling point and cooling below that causes the system to convert to a liquid, and you no longer have a gas.
Gay-Lussac's Law (constant n,V)
This is similar to Charles Law, except now instead of having a perfectly elastic container (that has no resistance to expansion or contraction) you have a rigid container of constant size. As T goes up the root mean velocity goes up and so the average kinetic energy goes up and thus the force imparted by collisions with the container are greater. Also, since the molecules tend to be moving faster (remember, there is a velocity profile), the collision frequency is greater.
Avogadro's Law (const P,T)
This describes an elastic container at isobaric and isothermal conditions. According to KMT increasing the number of particles increases the collision frequency on the surface which effectively increases the force. Since pressure (force per unit area) is constant, the system must expand (increase surface area) to accommodate the increased number of collisions.
Animation 10.5.1: Change the number of molecules and click the start button. Note how adding molecules increases the collision frequency. Since pressure is being kept equal, the system adjusts its volume so the collision frequency returns to the original value.
KMT and Ideal Gas Law
Qualitatively,KMT predicts:
- More particles means more collisions with the wall (P \(\propto n\))
- Smaller volume means more frequent collisions with the wall (\(P\propto\frac{1}{V}\))
- (P \(\propto T\))... the higher the temperature the faster the particles move, which increases both the collision frequency and the impact of each collision.
Putting all of these together yields
\[ P \propto \dfrac{nT}{V} =k \dfrac{nT}{V}\]
which can be rewritten as the familiar Ideal gas equation:
\[ PV=nRT\]


